Skip to main content
SpringerLink
Log in

A fully scalable algorithm suited for petascale computing and beyond

  • Special Issue Paper
  • Published:
Computer Science - Research and Development

Abstract

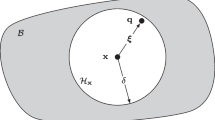
Nowadays supercomputers have already entered in the petascale computing era and peak rate performance is dramatically increasing year after year. However, most of current algorithms are not capable of exploiting fully such a technology due to the well-known parallel programming related issues, such as synchronization, communication and fault tolerance. The aim of this paper is to present a probabilistic domain decomposition algorithm based on generating suitable random trees for solving nonlinear parabolic partial differential equations. These are of paramount importance since many important scientific and engineering problems are modeled by such type of differential equations. We stress that such algorithm is perfectly suited for both current and future high performance supercomputers, showing a remarkable performance and arbitrary scalability.

While classical algorithms based on a deterministic domain decomposition exhibits strong limitations when increasing the size of the problem and the number of processors involved, probabilistic methods rather allow us to exploit efficiently massively parallel architectures, being the problem fully decoupled. Large-scale simulations runned on a high performance supercomputer confirm such properties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Acebrón JA, Busico MP, Lanucara P, Spigler R (2005) Domain decomposition solution of elliptic boundary-value problems. SIAM J Sci Comput 27(2):440–457

    Article  MATH  MathSciNet  Google Scholar 

  2. Acebrón JA, Busico MP, Lanucara P, Spigler R (2005) Probabilistically induced domain decomposition methods for elliptic boundary-value problems. J Comput Phys 210(2):421–438

    Article  MATH  MathSciNet  Google Scholar 

  3. Acebrón JA, Rodríguez-Rozas A, Spigler R (2009) Efficient parallel solution of nonlinear parabolic partial differential equations by a probabilistic domain decomposition. doi:10.1007/s10915-010-9349-2

  4. Acebrón JA, Rodríguez-Rozas A, Spigler R (2009) Domain decomposition solution of nonlinear two-dimensional parabolic problems by random trees. J Comput Phys 228(15):5574–5591

    Article  MATH  MathSciNet  Google Scholar 

  5. Antia HM (1995) Numerical methods for scientists and engineers. McGraw–Hill, New Delhi

    Google Scholar 

  6. Arbenz P, Cleary A, Dongarra J, Hegland M (1999) A comparison of parallel solvers for diagonally dominant and general narrow-banded linear systems. Parall Distrib Comput Pract 2(4):385–400

    Google Scholar 

  7. Arbenz P, Cleary A, Dongarra J, Hegland M (1999) A comparison of parallel solvers for diagonally dominant and general narrow-banded linear systems II, EuroPar ’99 parallel processing. Springer, Berlin, pp 1078–1087

    Google Scholar 

  8. Arnold L (1974) Stochastic differential equations: theory and applications. Wiley, New York

    MATH  Google Scholar 

  9. DuChateau P, Zachmann D (2002) Applied partial differential equations. Dover, New York

    Google Scholar 

  10. Freidlin M (1985) Functional integration and partial differential equations. Annals of mathematics studies, vol 109. Princeton Univ Press, Princeton

    MATH  Google Scholar 

  11. Karatzas I, Shreve SE (1991) Brownian motion and stochastic calculus, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  12. Keyes DE (2003) Domain decomposition methods in the mainstream of computational science, Proceedings of the 14th international conference on domain decomposition methods, UNAM Press, Mexico City, pp 79–93

    Google Scholar 

  13. Kloeden PE, Platen E (1992) Numerical solution of stochastic differential equations. Springer, Berlin

    MATH  Google Scholar 

  14. Petersen W, Arbenz P (2004) Introduction to parallel computing. A practical guide with examples in C. Oxford Univ Press, London

    MATH  Google Scholar 

  15. Quarteroni A, Valli A (1999) Domain decomposition methods for partial differential equations. Oxford Science Publications/Clarendon, Oxford

    MATH  Google Scholar 

  16. Poisson-Vlasov in a strong magnetic field: a stochastic solution approach R. Vilela Mendes arXiv:0904.2214 (April 2009)

  17. Waymire E (2005) Probability and incompressible Navier-Stokes equations: an overview of some recent developments. Prob Surv 2 1–32

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Mathematics and its Applications, Department of Mathematics, Instituto Superior Técnico, Av. Rovisco Pais, 1049-001, Lisbon, Portugal

    Juan A. Acebrón & Ángel Rodríguez-Rozas

  2. Dipartimento di Matematica, Università “Roma Tre”, Largo S.L. Murialdo 1, 00146, Rome, Italy

    Renato Spigler

Authors
  1. Juan A. Acebrón
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ángel Rodríguez-Rozas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Renato Spigler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juan A. Acebrón.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Acebrón, J.A., Rodríguez-Rozas, Á. & Spigler, R. A fully scalable algorithm suited for petascale computing and beyond. Comput Sci Res Dev 25, 115–121 (2010). https://doi.org/10.1007/s00450-010-0105-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00450-010-0105-5

Keywords

Search

Navigation