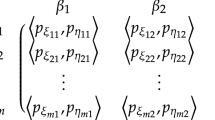Methods for solving matrix games with cross-evaluated payoffs

Abstract

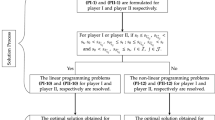
In the traditional fuzzy matrix game, given a pair of strategies, the payoffs of one player are usually associated with themselves, but not linked to the payoffs of the other player. Such payoffs can be called self-evaluated payoffs. However, according to the regret theory, the decision makers may care more about what they might get than what they get. Therefore, one player in a matrix game may pay more attention to the payoffs of the other player than his/her payoffs. In this paper, motivated by the pairwise comparison matrix, we allow the players to compare their payoffs and the other ones to provide their relative payoffs, which can be called the cross-evaluated payoffs. Moreover, the players’ preference about the cross-evaluated payoffs is usually distributed asymmetrically according to the law of diminishing utility. Then, the cross-evaluated payoffs of players can be expressed by using the asymmetrically distributed information, i.e., the interval-valued intuitionistic multiplicative number. Comparison laws are developed to compare the cross-evaluated payoffs of different players, and aggregation operators are introduced to obtain the expected cross-evaluated payoffs of players. Based on minimax and maximin principles, several mathematical programming models are established to obtain the solution of a matrix game with cross-evaluated payoffs. It is proved that the solution of a matrix game with cross-evaluated payoffs can be obtained by solving a pair of primal–dual linear-programming models and can avoid some unreasonable results. Two examples are finally given to illustrate that the proposed method is based on the cross-evaluated payoffs of players, and can directly provide the priority degree that one player is preferred to the other player in winning the game.

Appendices

Appendices

Proof of Theorem 1

The sufficient condition is obviously true. Next, if ${\tilde{\alpha }} _1 = {\tilde{\alpha }} _2$, then Definition 4 implies that $SF({\tilde{\alpha }} _1 ) = SF({\tilde{\alpha }} _2 ),AF({\tilde{\alpha }} _1 ) = AF({\tilde{\alpha }} _2 ),UI({\tilde{\alpha }} _1 ) = UI({\tilde{\alpha }} _2 )$ and $HI({\tilde{\alpha }} _1 ) = HI({\tilde{\alpha }} _2 )$. From the definitions of $SF( \cdot ),AF( \cdot ),UI( \cdot )$ and $HI( \cdot )$, we have

$$\begin{aligned} \sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + }}{{\sigma _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + }}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + }}{{\sigma _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + }}} ,\sqrt{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + \sigma _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + } = \sqrt{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + \sigma _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + } \end{aligned}$$

and

$$\begin{aligned} \sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ + \sigma _{{\tilde{\alpha }} _1 }^ - }}{{\rho _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + }}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _2 }^ + \sigma _{{\tilde{\alpha }} _2 }^ - }}{{\rho _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + }}} ,\sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ + \sigma _{{\tilde{\alpha }} _1 }^ + }}{{\rho _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ - }}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _2 }^ + \sigma _{{\tilde{\alpha }} _2 }^ + }}{{\rho _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ - }}} \end{aligned}$$

By solving these four equations, we have $\rho _{{\tilde{\alpha }} _1 }^ - = \rho _{{\tilde{\alpha }} _2 }^ - ,\rho _{{\tilde{\alpha }} _1 }^ + = \rho _{{\tilde{\alpha }} _2 }^ + ,\sigma _{{\tilde{\alpha }} _1 }^ - = \sigma _{{\tilde{\alpha }} _2 }^ -$ and $\sigma _{{\tilde{\alpha }} _1 }^ + = \sigma _{{\tilde{\alpha }} _2 }^ +$. $\square$

Proof of Theorem 2

According to Definition 6, if ${\tilde{\alpha }} _1 \succ _P {\tilde{\alpha }} _2$, then $\rho _{{\tilde{\alpha }} _1 }^ - \geqslant \rho _{{\tilde{\alpha }} _2 }^ - ,\rho _{{\tilde{\alpha }} _1 }^ + \geqslant \rho _{{\tilde{\alpha }} _2 }^ + ,\sigma _{{\tilde{\alpha }} _1 }^ - \leqslant \sigma _{{\tilde{\alpha }} _2 }^ -$ and $\sigma _{{\tilde{\alpha }} _1 }^ + \leqslant \sigma _{{\tilde{\alpha }} _2 }^ +$, and $SF({\tilde{\alpha }} _1 ) \geqslant SF({\tilde{\alpha }} _2 )$. Two cases will be discussed:

If $SF({\tilde{\alpha }} _1 ) > SF({\tilde{\alpha }} _2 )$, then ${\tilde{\alpha }} _1 \succ {\tilde{\alpha }} _2$;

If $SF({\tilde{\alpha }} _1 ) = SF({\tilde{\alpha }} _2 )$, then $\sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + }}{{\sigma _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + }}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + }}{{\sigma _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + }}}$, and

$$\begin{aligned} \frac{{AF({\tilde{\alpha }} _1 )}}{{AF({\tilde{\alpha }} _2 )}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + \sigma _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + }}{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + \sigma _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + }}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + \rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + }}{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + \rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + }}} = \frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + }}{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + }} \geqslant 1 \end{aligned}$$

which reduces to two cases:

If $AF({\tilde{\alpha }} _1 ) > AF({\tilde{\alpha }} _2 )$, then ${\tilde{\alpha }} _1 \succ {\tilde{\alpha }} _2$;

If $AF({\tilde{\alpha }} _1 ) = AF({\tilde{\alpha }} _2 )$, then $\sqrt{\frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + }}{{\sigma _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + }}} = \sqrt{\frac{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + }}{{\sigma _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + }}}$, and $\frac{{\rho _{{\tilde{\alpha }} _1 }^ - \rho _{{\tilde{\alpha }} _1 }^ + }}{{\rho _{{\tilde{\alpha }} _2 }^ - \rho _{{\tilde{\alpha }} _2 }^ + }} = 1$ , $\frac{{\sigma _{{\tilde{\alpha }} _1 }^ - \sigma _{{\tilde{\alpha }} _1 }^ + }}{{\sigma _{{\tilde{\alpha }} _2 }^ - \sigma _{{\tilde{\alpha }} _2 }^ + }} = 1$ , that is, $\frac{{\rho _{{\tilde{\alpha }} _1 }^ - }}{{\rho _{{\tilde{\alpha }} _2 }^ - }} = \frac{{\rho _{{\tilde{\alpha }} _2 }^ + }}{{\rho _{{\tilde{\alpha }} _1 }^ + }}$, $\frac{{\sigma _{{\tilde{\alpha }} _1 }^ - }}{{\sigma _{{\tilde{\alpha }} _2 }^ - }} = \frac{{\sigma _{{\tilde{\alpha }} _2 }^ + }}{{\sigma _{{\tilde{\alpha }} _1 }^ + }}$. Since $\rho _{{\tilde{\alpha }} _1 }^ - \geqslant \rho _{{\tilde{\alpha }} _2 }^ - ,\rho _{{\tilde{\alpha }} _1 }^ + \geqslant \rho _{{\tilde{\alpha }} _2 }^ + ,\sigma _{{\tilde{\alpha }} _1 }^ - \leqslant \sigma _{{\tilde{\alpha }} _2 }^ -$ and $\sigma _{{\tilde{\alpha }} _1 }^ + \leqslant \sigma _{{\tilde{\alpha }} _2 }^ +$, we have $\frac{{\rho _{{\tilde{\alpha }} _1 }^ - }}{{\rho _{{\tilde{\alpha }} _2 }^ - }} \geqslant 1,\frac{{\rho _{{\tilde{\alpha }} _2 }^ + }}{{\rho _{{\tilde{\alpha }} _1 }^ + }} \leqslant 1,\frac{{\sigma _{{\tilde{\alpha }} _1 }^ - }}{{\sigma _{{\tilde{\alpha }} _2 }^ - }} \leqslant 1,\frac{{\sigma _{{\tilde{\alpha }} _2 }^ + }}{{\sigma _{{\tilde{\alpha }} _1 }^ + }} \geqslant 1$, and then we have $\frac{{\rho _{{\tilde{\alpha }} _1 }^ - }}{{\rho _{{\tilde{\alpha }} _2 }^ - }} = \frac{{\rho _{{\tilde{\alpha }} _2 }^ + }}{{\rho _{{\tilde{\alpha }} _1 }^ + }} = 1,\frac{{\sigma _{{\tilde{\alpha }} _1 }^ - }}{{\sigma _{{\tilde{\alpha }} _2 }^ - }} = \frac{{\sigma _{{\tilde{\alpha }} _2 }^ + }}{{\sigma _{{\tilde{\alpha }} _1 }^ + }} = 1$; therefore, we have $\rho _{{\tilde{\alpha }} _1 }^ - = \rho _{{\tilde{\alpha }} _2 }^ - ,\rho _{{\tilde{\alpha }} _1 }^ + = \rho _{{\tilde{\alpha }} _2 }^ + ,\sigma _{{\tilde{\alpha }} _1 }^ - = \sigma _{{\tilde{\alpha }} _2 }^ -$ and $\sigma _{{\tilde{\alpha }} _1 }^ + = \sigma _{{\tilde{\alpha }} _2 }^ +$; hence, ${\tilde{\alpha }} _1 = {\tilde{\alpha }} _2$. That is to say, if ${\tilde{\alpha }} _1 \succ _P {\tilde{\alpha }} _2$, then we have ${\tilde{\alpha }} _1 \succ {\tilde{\alpha }} _2$.

$\square$

Proof of Theorem 3

For any $x \in X,y \in Y$, we have $\mathop {\max }\nolimits _{x \in X} \{ \varphi ^ - \} \geqslant \varphi ^ - \geqslant \mathop {\min }\nolimits _{y \in Y} \{ \varphi ^ - \}$; hence, $\mathop {\min }\nolimits _{y \in Y} \mathop {\max }\nolimits _{x \in X} \{ \varphi ^ - \} \geqslant \mathop {\min }\nolimits _{y \in Y} \{ \varphi ^ - \}$. Therefore, $\mathop {\min }\nolimits _{y \in Y} \mathop {\max }\nolimits _{x \in X} \{ \varphi ^ - \} \geqslant \mathop {\max }\nolimits _{x \in X} \mathop {\min }\nolimits _{y \in Y} \{ \varphi ^ - \}$. Similarly, it also follows that $\mathop {\min }\nolimits _{y \in Y} \mathop {\max }\nolimits _{x \in X} \{ \varphi ^ + \} \geqslant \mathop {\max }\nolimits _{x \in X} \mathop {\min }\nolimits _{y \in Y} \{ \varphi ^ + \}$. According to Definitions 5 and 6, we have

$$\begin{aligned} \mathop {\min }\limits _{y \in Y} \mathop {\max }\limits _{x \in X} \{ {[}\varphi ^ - ,\varphi ^ + ]\} \succ \mathop {\max }\limits _{x \in X} \mathop {\min }\limits _{y \in Y} \{ [\varphi ^ - ,\varphi ^ + {]}\} \end{aligned}$$

(3)

On the other hand, for any $x \in X$ and $y \in Y$, we have $\mathop {\max }\nolimits _{y \in Y} \{ \phi _{xy}^ - \} \geqslant \phi _{xy}^ - \geqslant \mathop {\min }\nolimits _{x \in X} \{ \phi _{xy}^ - \}$; hence, $\mathop {\max }\nolimits _{y \in Y} \{ \phi _{xy}^ - \} \geqslant \mathop {\max }\nolimits _{y \in Y} \mathop {\min }\nolimits _{x \in X} \{ \phi _{xy}^ - \}$. Therefore, $\mathop {\min }\nolimits _{y \in Y} \mathop {\max }\nolimits _{y \in Y} \{ \phi _{xy}^ - \} \geqslant \mathop {\max }\nolimits _{y \in Y} \mathop {\min }\nolimits _{x \in X} \{ \phi _{xy}^ - \}$. Similarly, it follows that $\mathop {\min }\nolimits _{y \in Y} \mathop {\max }\nolimits _{y \in Y} \{ \phi _{xy}^ + \} \geqslant \mathop {\max }\nolimits _{y \in Y} \mathop {\min }\nolimits _{x \in X} \{ \phi _{xy}^ + \}$. According to Definitions 5 and 6, we have

$$\begin{aligned} \mathop {\min }\limits _{y \in Y} \mathop {\max }\limits _{y \in Y} \{ {[}\phi _{xy}^ - ,\phi _{xy}^ + ]\} \succ \mathop {\max }\limits _{y \in Y} \mathop {\min }\limits _{x \in X} \{ [\phi _{xy}^ - ,\phi _{xy}^ + ]\} \end{aligned}$$

(4)

Combining Eqs. (3) and (4), we have

$$\begin{aligned}&\mathop {\min }\limits _{y \in Y} \mathop {\max }\limits _{x \in X} \{ ([\varphi _{xy}^ - ,\varphi _{xy}^ + ],[\phi _{xy}^ - ,\phi _{xy}^ + ])\} \\&\quad \succ \, _P \mathop {\max }\limits _{x \in X} \mathop {\min }\limits _{y \in Y} \{ ([\varphi _{xy}^ - ,\varphi _{xy}^ + {]},[\phi _{xy}^ - ,\phi _{xy}^ + ])\} \end{aligned}$$

i.e., $\vartheta ^* \succ _P \theta ^*$. $\square$

Proof of Theorem 4

If $\theta ^* = \vartheta ^*$, then $\mathop {\max }\nolimits _{x \in X} \mathop {\min }\nolimits _{y \in Y} \{ x^{\mathrm{T}} Ay\} = \mathop {\min }\nolimits _{y \in Y} \mathop {\max }\nolimits _{x \in X} \{ x^\mathrm{T} Ay\}$, which shows there exist $(x^* ,y^* )(x^* \in X,y^* \in Y)$ such that $\mathop {\max }\nolimits _{x \in X} \mathop {\min }\nolimits _{y \in Y} \{ x^{\mathrm{T}} Ay\} =\mathop {\min }\nolimits _{y \in Y} \{ x^{*\mathrm T} Ay\}$ and $\mathop {\min }\nolimits _{y\in Y}\mathop {\max }\nolimits _{x\in X}\{x^\mathrm{T}Ay\}=\mathop {\max }\nolimits _{x\in X}\{x^{\mathrm{T}}Ay^*\}$; therefore, $\mathop {\min }\nolimits _{y\in Y}\{x^{*\mathrm T}Ay\}=\mathop {\max }\nolimits _{x\in X}\{x^{\mathrm{T}}Ay^*\}$. Since $x^{*\mathrm T}Ay^*\succ _P\mathop {\min }\nolimits _{y\in Y}\{x^{*\mathrm T}Ay\}$ and $\mathop {\max }\nolimits _{x\in X}\{x^{\mathrm{T}} Ay^*\}\succ _P x^{*\mathrm T}Ay^*$, we have $\mathop {\max }\nolimits _{x \in X}\{ x^\mathrm{T}Ay^*\}=x^{*\mathrm T} Ay^*=\mathop {\min }\nolimits _{y\in Y}\{x^{*\mathrm T}Ay\}$, which indicates that $x^{*\mathrm{T}}Ay\succ _P x^{*\mathrm{T}}Ay^*\succ _P x^{\mathrm{T}}Ay^*$, and $(x^*,y^*,x^{*\mathrm{T}} Ay^*)$ is the solution of matrix game A.

On the other side, if $(x^* ,y^* ,x^{*\mathrm{T}} Ay^* )$ is the solution of matrix game A, and $x^{*\mathrm{T}}Ay\succ _P x^{*\mathrm{T}} Ay^*\succ _P x^{\mathrm{T}} Ay^*$, for any $x \in X$ and $y \in Y$, we have $\mathop {\max }\nolimits _{x\in X}\mathop {\min }\nolimits _{y\in Y}\{x^{\mathrm{T}}Ay\}\succ _P x^{{\text {*}}\mathrm{T}}Ay^{\text {*}}\succ _P\mathop {\min }\nolimits _{y\in Y}\mathop {\max }\nolimits _{x\in X}\{x^{\mathrm{T}}Ay\}$. Therefore, $\mathop {\max }\nolimits _{x\in X}\mathop {\min }\nolimits _{y\in Y}\{x^\mathrm{T} Ay\}\succ _P \mathop {\min }\nolimits _{y\in Y}\mathop {\max }\nolimits _{x\in X}\{ x^{\mathrm{T}}Ay\}$. According to Theorem 3, we have $\mathop {\min }\nolimits _{y\in Y}\mathop {\max }\nolimits _{x\in X}\{x^{\mathrm{T}}Ay\}\succ _P\mathop {\max }\nolimits _{x\in X}\mathop {\min }\nolimits _{y\in Y}\{x^\mathrm{T}Ay\}$ and then $\mathop {\max }\nolimits _{x\in X}\mathop {\min }\nolimits _{y\in Y}\{x^\mathrm{T}Ay\}{\text {=}}\mathop {\min }\nolimits _{y\in Y}\mathop {\max }\nolimits _{x\in X}\{x^{\mathrm{T}}Ay\}$, which completes the proof. $\square$

Proof of Theorem 5

For any $\lambda \in [0,1]$, obviously, (MOD-5) and (MOD-10) are a pair of dual–primal linear-programming models corresponding to the matrix game with the payoff matrix

$$\begin{aligned} D= & {} (d_{ij} )_{m \times n} = \left( \lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ - )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ - ))\right. \\&\left. + \lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ + ))+\, (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ + )) \right) _{m \times n} \end{aligned}$$

According to the minimax theorem (Owen 1982), every matrix game has a solution, which can be obtained by formulating a pair of primal–dual linear-programming models ((MOD-5) and (MOD-10)). Suppose the solution of matrix game D is denoted as $(x^* ,y^* ,v^* )$, then $x^*$ and $y^*$ are the optimal solutions of (MOD-5) and (MOD-10), respectively. $v^*$ is the common optimal value of (MOD-5) and (MOD-10), that is, $v^* = \tau ^* = \varsigma ^*$. $\square$

Proof of Theorem 6

Since $\tau ^ - = \lambda \ln (h(\rho ^ - )) + (1 - \lambda )\ln (g(\sigma ^ + ))$ and $\tau ^ + = \lambda \ln (h(\rho ^ + )) + (1 - \lambda )\ln (g(\sigma ^ - ))$, we have $\tau = \tau ^ - + \tau ^ + = \lambda \ln (h(\rho ^ - )) + (1 - \lambda )\ln (g(\sigma ^ + )){\text { + }}\lambda \ln (h(\rho ^{\text { + }} )) + (1 - \lambda )\ln (g(\sigma ^ - ))$, where $0 \leqslant \rho ^ - \leqslant \rho ^ + < 1$, and $0 \leqslant \sigma ^ - \leqslant \sigma ^ + < 1$. Then, the partial differential of $\tau$ with respect to $\lambda$ is computed as follows:

$$\begin{aligned} \frac{{\partial \tau }}{{\partial \lambda }} = \ln (h(\rho ^ - )) - \ln (g(\sigma ^ + )){\text { + }}\ln (h(\rho ^{\text { + }} )) - \ln (g(\sigma ^ - )) \end{aligned}$$

Since $\rho ^ - \sigma ^ - \leqslant \rho ^ + \sigma ^ + \leqslant 1$, we have $\rho ^ - \leqslant \frac{1}{{\sigma ^ - }}$, $\rho ^ + \leqslant \frac{1}{{\sigma ^ + }}$,

$$\begin{aligned} \ln (h(\rho ^ - )) - \ln (g(\sigma ^ - ))\leqslant & {} \ln (h(\frac{{\text {1}}}{{\sigma ^ - }})) - \ln (g(\sigma ^ - ))\\= & {} \ln (g(\sigma ^ - )) - \ln (g(\sigma ^ - )) = 0 \end{aligned}$$

and

$$\begin{aligned} \ln (h(\rho ^{\text {+}} )) - \ln (g(\sigma ^{\text {+}} ))\leqslant & {} \ln (h(\frac{{\text {1}}}{{\sigma ^{\text {+}} }})) - \ln (g(\sigma ^{+} )) \\= & {} \ln (g(\sigma ^{\text {+}} )) - \ln (g(\sigma ^{\text {+}} )) = 0 \end{aligned}$$

which follows that $\frac{{\partial \tau }}{{\partial \lambda }} \leqslant 0$. Therefore, $\tau$ is a monotonic and decreasing function of $\lambda \in [0,1]$.

Similarly, since $\varsigma ^ - = \lambda \ln (h(\mu ^ - )) + (1 - \lambda )(\ln (g(\nu ^ + ))$ and $\varsigma ^ + = \lambda \ln (h(\mu ^{\text { + }} )) + (1 - \lambda )(\ln (g(\nu ^ - ))$, we have $\varsigma = \varsigma ^ - + \varsigma ^ + = \lambda \ln (h(\mu ^ - )) + (1 - \lambda )\ln (g(\nu ^ + )){\text { + }}\lambda \ln (h(\mu ^ + )) + (1 - \lambda )\ln (g(\nu ^ - ))$, where $0 \leqslant \mu ^ - \leqslant \mu ^ + < 1$, and $0 \leqslant \nu ^ - \leqslant \nu ^ + < 1$. Then, the partial differential of $\varsigma$ with respect to $\lambda$ is computed as follows:

$$\begin{aligned} \frac{{\partial \varsigma }}{{\partial \lambda }} = \ln (h(\mu ^ - )) - \ln (g(\nu ^{\text { + }} )) + \ln (h(\mu ^ + )) - \ln (g(\nu ^ - )) \end{aligned}$$

Since $\mu ^ - \nu ^ - \leqslant \mu ^ + \nu ^ + \leqslant 1$, we have $\mu ^ - \leqslant \frac{1}{{\nu ^ - }}$, $\mu ^ + \leqslant \frac{1}{{\nu ^ + }}$,

$$\begin{aligned} \ln (h(\mu ^ - )) - \ln (g(\nu ^ - ))\leqslant & {} \ln (h(\frac{{\text {1}}}{{\nu ^ - }})) - \ln (g(\nu ^ - )) \\= & {} \ln (g(\nu ^ - )) - \ln (g(\nu ^ - )) = 0 \end{aligned}$$

and

$$\begin{aligned} \ln (h(\mu ^{\text { + }} )) - \ln (g(\nu ^{\text { + }} ))\leqslant & {} \ln \left( h\left( \frac{{\text {1}}}{{\nu ^{\text { + }} }}\right) \right) - \ln (g(\nu ^{\text { + }} ))\\= & {} \ln (g(\nu ^{\text { + }} )) - \ln (g(\nu ^{\text { + }} )) = 0 \end{aligned}$$

which follows that $\frac{{\partial \varsigma }}{{\partial \lambda }} \leqslant 0$. Therefore, $\varsigma$ is a monotonic and decreasing function of $\lambda \in [0,1]$. $\square$

Proof of Theorem 7

Suppose that $(x^* ,\theta ^* )$ is not a Pareto optimal/non-inferior solution of (MOD-1), where $\theta ^* = \mathop {\min }\nolimits _{y \in Y} \{ x^* Ay\} = ([\rho _*^ - ,\rho _*^ + ],[\sigma _*^ - ,\sigma _*^+])$. Then, there exists a feasible solution $({\hat{x}},{\hat{\theta }} )$, where ${\hat{x}} \in X$, and ${\hat{\theta }} = \mathop {\min }\nolimits _{y \in Y} \{ {\hat{x}} Ay\} = ( [\hat{\rho } ^ - ,{\hat{\rho }} ^ + ],[{\hat{\sigma }} ^ - ,{\hat{\sigma }} ^ + ] )$ such that

$$\begin{aligned} \left\{ \begin{aligned}&h^{ - 1} \left( {\prod \limits _{j = 1}^n {\prod \limits _{i = 1}^m {(h(\rho _{{\tilde{\alpha }} _{ij} }^ - ))^{{\hat{x}} _i y_j } } } } \right) \geqslant {\hat{\rho }} ^ - , y \in Y&\\&h^{ - 1} \left( {\prod \limits _{j = 1}^n {\prod \limits _{i = 1}^m {(h(\rho _{{\tilde{\alpha }} _{ij} }^ + ))^{{\hat{x}} _i y_j } } } } \right) \geqslant {\hat{\rho }} ^ + , y \in Y&\\&g^{ - 1} \left( {\prod \limits _{j = 1}^n {\prod \limits _{i = 1}^m {(g(\sigma _{{\tilde{\alpha }} _{ij} }^ - ))^{{\hat{x}} _i y_j } } } } \right) \leqslant {\hat{\sigma }} ^ + , y \in Y&\\&g^{ - 1} \left( {\prod \limits _{j = 1}^n {\prod \limits _{i = 1}^m {(g(\sigma _{{\tilde{\alpha }} _{ij} }^ + ))^{{\hat{x}} _i y_j } } } } \right) \leqslant {\hat{\sigma }} ^ + , y \in Y&\\&0 \leqslant {\hat{\rho }} ^ + + {\hat{\sigma }} ^ + \leqslant 1,\sum \limits _{i = 1}^n {{\hat{x}} _i } = 1&\\&{\hat{\rho }} ^ - \geqslant 0,{\hat{\rho }} ^ + \geqslant 0,{\hat{\sigma }} ^ - \geqslant 0,{\hat{\sigma }} ^ + \geqslant 0,\\&\quad {\hat{x}} _i \geqslant 0,i = 1,2, \ldots ,m&\\ \end{aligned} \right. \end{aligned}$$

and $[{\hat{\rho }} ^ - ,{\hat{\rho }} ^ + ] \succ [\rho _*^ - ,{\hat{\rho }} _*^ + ]$, $[{\hat{\sigma }} ^ - ,{\hat{\sigma }} ^ + {]} \prec [\sigma _*^ - ,\sigma _*^ + ]$, at least one of which is strictly valid. Let $\lambda \in [0,1]$, and we have

$$\begin{aligned} \left\{ \begin{aligned}&\sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {{\hat{x}} _i y_j (\lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ - )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ - )))} } \\&\quad \geqslant \lambda \ln (h({\hat{\rho }} ^ - )) + (1 - \lambda )\ln (g({\hat{\sigma }} ^ - )), y \in Y\\&\sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {{\hat{x}} _i y_j (\lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ + )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ + )))} } \\&\quad \geqslant \lambda \ln (h({\hat{\rho }} ^ + )) + (1 - \lambda )\ln (g({\hat{\sigma }} ^ + )), y \in Y \\&0 \leqslant {\hat{\rho }} ^ + + {\hat{\sigma }} ^ + \leqslant 1,\sum \limits _{i = 1}^n {{\hat{x}} _i } = 1&\\&{\hat{\rho }} ^ - \geqslant 0,{\hat{\rho }} ^ + \geqslant 0,{\hat{\sigma }} ^ - \geqslant 0,{\hat{\sigma }} ^ + \geqslant 0,\\&\quad {\hat{x}} _i\geqslant 0,i = 1,2, \ldots ,m&\\ \end{aligned} \right. \end{aligned}$$

(5)

$$\begin{aligned}&\lambda \ln (h({\hat{\rho }} ^ - )) + (1 - \lambda )\ln (g({\hat{\sigma }} ^ - )) \\&\quad \geqslant \lambda \ln (h(\rho _*^ - )) + (1 - \lambda )\ln (g(\sigma _*^ - )) \end{aligned}$$

and

$$\begin{aligned}&\lambda \ln (h({\hat{\rho }} ^ + )) + (1 - \lambda )\ln (g({\hat{\sigma }} ^ + )) \\&\quad \geqslant \lambda \ln (h(\rho _*^ + )) + (1 - \lambda )\ln (g(\sigma _*^ + )) \end{aligned}$$

Let

$$\begin{aligned} {\hat{\tau }} ^ -= & {} \lambda \ln (h({\hat{\rho }} ^ - )) + (1 - \lambda )\ln (g({\hat{\sigma }} ^ - ))\\ {\hat{\tau }} ^ += & {} \lambda \ln (h({\hat{\rho }} ^ + )) + (1 - \lambda )\ln (g({\hat{\sigma }} ^ + ))\\ \tau _*^ -= & {} \lambda \ln (h(\rho _*^ - )) + (1 - \lambda )\ln (g(\sigma _*^ - )) \end{aligned}$$

and

$$\begin{aligned} \tau _*^ + = \lambda \ln (h(\rho _*^ + )) + (1 - \lambda )\ln (g(\sigma _*^ + )) \end{aligned}$$

which follows that ${\hat{\tau }} ^ - \geqslant \tau _*^ -$, ${\hat{\tau }} ^ + \geqslant \tau _*^ +$, and at least one of the inequalities is strictly valid. Hence, we have ${\hat{\tau }} ^ - + {\hat{\tau }} ^ + \geqslant \tau _*^ - + \tau _*^ +$.

Since Y is a finite and compact convex set, it is reasonable to consider only the extreme points of the set Y. Thus, Eq. (5) is transformed into the following:

$$\begin{aligned} \left\{ \begin{aligned}&\sum \limits _{i = 1}^m {{\hat{x}} _i (\lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ - )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ - )))} \geqslant {\hat{\tau }} ^ - , \\&\quad j = 1,2, \ldots ,n \\&\sum \limits _{i = 1}^m {{\hat{x}} _i (\lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ + )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ + )))} \geqslant {\hat{\tau }} ^ +, \\&\quad j = 1,2, \ldots ,n \\&\sum \limits _{i = 1}^m {{\hat{x}} _i } = 1&\\&{\hat{x}} _i \geqslant 0,i = 1,2, \ldots ,m&\\ \end{aligned} \right. \end{aligned}$$

which is equivalent to:

$$\begin{aligned} \left\{ \begin{aligned}&\sum \limits _{i = 1}^m {\hat{x}} _i (\lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ - )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ - )) + \lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ + )) \\&\quad +\, (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ + ))) \geqslant {\hat{\tau }} ^ - + {\hat{\tau }} ^ + , j = 1,2, \ldots ,n\\&\sum \limits _{i = 1}^m {{\hat{x}} _i } = 1&\\&{\hat{x}} _i \geqslant 0,i = 1,2, \ldots ,m&\\ \end{aligned} \right. \end{aligned}$$

(6)

Let ${\hat{\tau }} = {\hat{\tau }} ^ - + {\hat{\tau }} ^ +$, and then Eq. (6) is rewritten as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\sum \limits _{i = 1}^m {\hat{x}} _i (\lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ - )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ - ))\\&\quad + \lambda \ln (h(\rho _{{\tilde{\alpha }} _{ij} }^ + )) + (1 - \lambda )\ln (g(\sigma _{{\tilde{\alpha }} _{ij} }^ + )))\geqslant {\hat{\tau }} ,\\&\qquad j = 1,2, \ldots ,n&\\&\sum \limits _{i = 1}^m {{\hat{x}} _i } = 1&\\&{\hat{x}} _i \geqslant 0,i = 1,2, \ldots ,m&\\ \end{aligned} \right. \end{aligned}$$

i.e., $({\hat{x}} ,{\hat{\tau }} )$ is a feasible solution of (MOD-5), and ${\hat{\tau }} > \tau ^*$. Therefore, there exists a contradiction with the fact that $(x^* ,\tau ^* )$ is the optimal solution of (MOD-1). Therefore, $(x^* ,\theta ^* )$ is a Pareto optimal/non-inferior solution of (MOD-1). Similarly, we can prove that $(y^* ,\vartheta ^* )$ is a non-inferior solution of (MOD-6).

Proof of Theorem 8

Based on Theorems 5 and 7, we have $\tau ^* = \varsigma ^*$, and

$$\begin{aligned} \tau ^*= & {} \lambda (\ln (h(\rho _*^ - )) + \ln (h(\rho _*^ + )))\\&+\, (1 - \lambda )(\ln (g(\sigma _*^ - )) + \ln (g(\sigma _*^ + ))) \end{aligned}$$

and

$$\begin{aligned} \varsigma ^*= & {} \lambda (\ln (h(\mu _*^ - )) + \ln (h(\mu _*^ + ))) \\&+ \,(1 - \lambda )(\ln (g(\nu _*^ - )) + \ln (g(\nu _*^ + ))) \end{aligned}$$

Therefore,

$$\begin{aligned}&\lambda (\ln (h(\rho _*^ - )) + \ln (h(\rho _*^ + ))) \\&\qquad + \,(1 - \lambda )(\ln (g(\sigma _*^ - )) + \ln (g(\sigma _*^ + )))\\&\quad = \lambda (\ln (h(\mu _*^ - )) + \ln (h(\mu _*^ + ))) \\&\qquad + \,(1 - \lambda )(\ln (g(\nu _*^ - )) + \ln (g(\nu _*^ + ))) \end{aligned}$$

Then,

$$\begin{aligned} \ln (h(\rho _*^ - )) + \ln (h(\rho _*^ + )) = \ln (h(\mu _*^ - )) + \ln (h(\mu _*^ + )) \end{aligned}$$

and

$$\begin{aligned} \ln (g(\sigma _*^ - )) + \ln (g(\sigma _*^ + )) = \ln (g(\nu _*^ - )) + \ln (g(\nu _*^ + )) \end{aligned}$$

Based on Theorem 3, we have $\vartheta ^* \succ _P \theta ^*$, that is, $\mu _*^ - \geqslant \rho _*^ -$, $\mu _*^ + \geqslant \rho _*^ +$, $\nu _*^ - \leqslant \sigma _*^ -$ and $\nu _*^ + \leqslant \sigma _*^ +$ Therefore, $\rho _*^ - = \mu _*^ -$, $\rho _*^ + = \mu _*^ +$, $\sigma _*^ - = \nu _*^ -$ and $\sigma _*^ + = \nu _*^ +$, which indicates that $\theta ^* = \vartheta ^*$.

Since

$$\begin{aligned} \theta ^*= & {} \mathop {\max }\limits _{x \in X} \mathop {\min }\limits _{y \in Y} \sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {x_i y_j {\tilde{\alpha }} _{ij} } } \\= & {} \mathop {\min }\limits _{y \in Y} \sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {x_i^* y_j {\tilde{\alpha }} _{ij} } } \prec _P \sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {x_i^* y_j^* {\tilde{\alpha }} _{ij} } } \end{aligned}$$

and

$$\begin{aligned} \vartheta ^*= & {} \mathop {\min }\limits _{y \in Y} \mathop {\max }\limits _{x \in X} \sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {x_i y_j {\tilde{\alpha }} _{ij} } } \\= & {} \mathop {\max }\limits _{y \in Y} \sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {x_i y_j^* {\tilde{\alpha }} _{ij} } } \succ _P \sum \limits _{j = 1}^n {\sum \limits _{i = 1}^m {x_i^* y_j^* {\tilde{\alpha }} _{ij} } } \end{aligned}$$

we have $\theta ^* = \vartheta ^* = \sum \nolimits _{j = 1}^n {\sum \nolimits _{i = 1}^m {x_i^* y_j^* {\tilde{\alpha }} _{ij} } } = x^* Ay^*$. According to Definition 10, we can conclude that $(x^*, y^* ,x^* Ay^* )$ is a solution of the matrix game A.