Feedforward neural network for blind equalization with PSK signals

Abstract

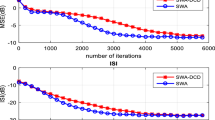
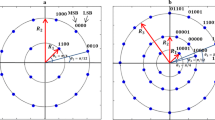
Most of the cost functions used for blind equalization are nonconvex and nonlinear functions of tap weights, when implemented using linear transversal filter structures. Therefore, a blind equalization scheme with a nonlinear structure that can form nonconvex decision regions is desirable. The efficacy of complex-valued feedforward neural networks for blind equalization of linear and nonlinear communication channels has been confirmed by many studies. In this paper we present a complex valued neural network for blind equalization with M-ary phase shift keying (PSK) signals. The complex nonlinear activation functions used in the neural network are especially defined for handling the M-ary PSK signals. The training algorithm based on constant modulus algorithm (CMA) cost function is derived. The improved performance of the proposed neural network in both, stationary and nonstationary environments, is confirmed through computer simulations.

Appendix

The CMA cost function is expressed as

$$J(n) = \frac{1}{4}E{\left[ {{\left({{\left| {y(n)} \right|}^{2} - R_{2}} \right)}^{2}} \right]},$$

(25)

where

$$R_{2} = \frac{E[{\left| {s(n)} \right|}^{4} ]}{E[{\left| {s(n)} \right|}^{2} ]}.$$

Using the gradient descent technique, the weights of the neural network can be updated as

$$w^{{(2)}}_{k} (n + 1) = w^{{(2)}}_{k} (n) - \eta \nabla _{{w^{{(2)}}_{k}}} J(n)$$

(26)

and

$$w^{{(1)}}_{{kl}} (n + 1) = w^{{(1)}}_{{kl}} (n) - \eta \nabla _{{w^{{(1)}}_{{kl}}}} J(n),$$

(27)

where η is the learning rate parameter and the terms $\nabla_{{w^{(2)}_{k}}} J(n)$ and $\nabla _{{w^{(1)}_{{kl}}}} J(n)$ represent the gradients of the cost function J(n) defined by (25) with respect to the weights w⁽²⁾ _k and w⁽¹⁾ _kl , respectively.

Since the activation function of the output layer neuron for M-ary PSK signal is defined in terms of modulus and angle of the activation sum, the gradient of the CMA cost function with respect to the output layer weight w⁽²⁾ _k (n) is expressed as

$$\nabla _{{w^{{(2)}}_{k}}} J(n) = ({\left| {y(n)} \right|}^{2} - R_{2})\,{\left| {y(n)} \right|}\,{\left({ab - \frac{b}{a}{\left| {y(n)} \right|}^{2}} \right)}\frac{{\partial {\rm net}^{{(2)}} (n)}}{{\partial w^{{(2)}}_{k} (n)}}.$$

(28)

To obtain an expression for the partial derivative of (28), we use the relationship

$${\left| {{\rm net}^{{(2)}} (n)} \right|}^{2} = {\left({{\rm net}^{{(2)}}_{\rm R} (n)} \right)}^{2} + {\left({{\rm net}^{{(2)}}_{\rm I} (n)} \right)}^{2}. $$

(29)

On differentiating (29) with respect to w⁽²⁾ _k , we get

$$\begin{aligned} \frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}} {{\partial w^{{(2)}}_{k} (n)}} = & \frac{1} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left[ {{\rm net}^{{(2)}}_{\rm R} (n)\,\frac{{\partial {\rm net}^{{(2)}}_{\rm R} (n)}} {{\partial w^{{(2)}}_{k} (n)}} + {\rm net}^{{(2)}}_{\rm I} (n)\frac{{\partial {\rm net}^{{(2)}}_{\rm I} (n)}} {{\partial w^{{(2)}}_{k} (n)}}} \right]} \\ = & \frac{1} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left[ {{\rm net}^{{(2)}}_{\rm R} (n){\left( {\varphi ^{{(1)}} (net^{{(1)}}_{{k,{\rm R}}} (n)) - j\varphi ^{{(1)}} ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))} \right)} + {\rm net}^{{(2)}}_{\rm I} (n){\left( {\varphi ^{{(1)}} ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n)) + j\varphi ^{{(1)}} ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))} \right)}} \right]} \\ = & \frac{{\varphi ^{{(1)*}} ({\rm net}^{{(1)}}_{k} (n)){\rm net}^{{(2)}} (n)}} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}} \\ \end{aligned} $$

(30)

On substituting (30) in (28), the expression for the gradient becomes

$$\nabla _{{w^{{(2)}}_{k}}} J(n) = \delta ^{{(2)}} (n) u^{*}_{k} (n)$$

(31)

where

$$\delta ^{{(2)}} (n) = {\left[ {{\left({{\left| {y(n)} \right|}^{2} - R_{2}} \right)}{\left| {y(n)} \right|}{\left({ab - \frac{b}{a}{\left| {y(n)} \right|}^{2}} \right)}} \right]}\frac{{{\rm net}^{{(2)}} (n)}}{{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}.$$

(32)

Substitution of (31) in (26) along with (32) gives the update equation (17) with (18) for M-ary PSK signal.

In order to obtain the update equation for the weights {w⁽¹⁾ _kl }, we need the following gradient

$$\nabla _{{w^{{(1)}}_{{kl}}}} J(n) = {\left({{\left| {y(n)} \right|}^{2} - R_{2}} \right)}\,{\left| {y(n)} \right|}\,{\left({ab - \frac{b}{a}{\left| {y(n)} \right|}^{2}} \right)}\frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}}{{\partial w^{{(1)}}_{{kl}} (n)}}.$$

(33)

The partial derivative terms in (33) can be obtained by using (29)

$$\frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}}{{\partial w^{{(1)}}_{{kl}} (n)}} = \frac{1}{{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left[ {{\rm net}^{{(2)}}_{\rm R} (n)\frac{{\partial {\rm net}^{{(2)}}_{\rm R} (n)}}{{\partial w^{{(1)}}_{{kl}} (n)}} + {\rm net}^{{(2)}}_{\rm I} (n)\frac{{\partial {\rm net}^{{(2)}}_{\rm I} (n)}}{{\partial w^{{(1)}}_{{kl}}(n)}}} \right]},$$

(34)

where

$$\begin{aligned} \frac{{\partial {\rm net}^{{(2)}}_{\rm R} (n)}} {{\partial w^{{(1)}}_{{kl}} (n)}} = & w^{{(2)}}_{{k,{\rm R}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n)).(x_{{l,{\rm R}}} (n) - jx_{{l,{\rm I}}} (n)) \\ & - w^{{(2)}}_{{k,{\rm I}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))(x_{{l,{\rm I}}} (n) + jx_{{l,{\rm R}}} (n)) \\ \end{aligned} $$

(35)

and

$$\begin{aligned} \frac{{\partial {\rm net}^{{(2)}}_{\rm I} (n)}} {{\partial w^{{(1)}}_{{kl}} (n)}} = & w^{{(2)}}_{{k,{\rm R}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))(x_{{l,{\rm I}}} (n) + jx_{{l,{\rm R}}} (n)) \\ & + w^{{(2)}}_{{k,{\rm I}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))(x_{{l,{\rm R}}} (n) - jx_{{l,{\rm I}}} (n)) \\ \end{aligned}. $$

(36)

Now the substitution of (35) and (36) in (34) and some simplification lead to

$$\frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}} {{\partial w^{{(1)}}_{{kl}} (n)}} = \frac{{x^{*}_{l} (n)}} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left( {{\varphi ^{(1)} }^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\,\operatorname{Re} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)] - j{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\,\operatorname{Im} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)]} \right)}. $$

(37)

Finally, by substituting (37) in (33), we get

$$\begin{aligned} \nabla _{{w^{{(1)}}_{{kl}} }} J(n) = & \delta ^{{(2)}} (n)x^{*}_{l} (n){\left( {{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\,\operatorname{Re} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)] - j{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\,\operatorname{Im} [w^{{(2)}}_{k} (n)net^{{(2)*}} (n)]} \right)} \\ = & \delta ^{{(1)}}_{k} (n)x^{*}_{l} (n) \\ \end{aligned} $$

(38)

where

$$\delta ^{{(1)}}_{k} (n) = \frac{{\delta ^{{(2)}} (n)}}{{{\rm net}^{{(2)}} (n)}}{\left( {{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\,\operatorname{Re} [w^{{(2)}}_{k} (n)net^{{(2)*}} (n)] - j{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\,\operatorname{Im} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)]} \right)}.$$

Using (38) and (27), we get the update rule of (19) for M-ary PSK signal.