Skip to main content
SpringerLink
Log in

Chaos and rigorous verification of horseshoes in a class of Hopfield neural networks

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

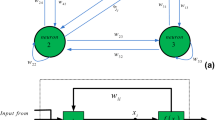
In this paper, chaos in a new class of three-dimensional continuous time Hopfield neural networks is investigated. Numerical experiments show that this class of Hopfield neural networks can have chaotic attractors and limit cycles for different parameter configurations. By virtue of horseshoes theory in dynamic systems, rigorous computer-assisted verifications are done for their chaotic behavior. In terms of topological entropy, quantitative interpretations of these neural networks’ complexity are given. A brief analysis is also presented about their robustness.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Hopfield JJ (1982) Neural networks and physical system with emergent collective computational abilities. Proc Natl Acad Sci USA 79:2554–2558. doi:10.1073/pnas.79.8.2554

    Article  MathSciNet  Google Scholar 

  2. Amari S (1990) Mathematical foundations of neurocomputing. Proc IEEE 78:1443–1448. doi:10.1109/5.58324

    Article  Google Scholar 

  3. Doi S, Kumagai S (2005) Generation of very slow neuronal rhythms and chaos near the Hopf bifurcation in single neuron models. J Comput Neurosci 19(3). doi:10.1007/s10827-005-2895-1

  4. He G, Shrimali MD, Aihara K (2007) Partial state feedback control of chaotic neural network and its application. Phys Lett A 371(3):228–233

    Google Scholar 

  5. Korn H, Faure P (2003) Is there chaos in the brain? II. Experimental evidence and related models. C R Biol 326:785–840

    Article  Google Scholar 

  6. Wu WJ, Chen ZQ, Yuan ZZ (2008) A computer-assisted proof for the existence of horseshoe in a novel chaotic system. Chaos Solitons Fractals. http://www.elsvier.com/locate/chaos. Accessed 22 November 2008

  7. Yuan Q, Li Q, Yang X-S (2008) Horseshoe in a model of artificial neural network. Appl Math Model 32(7):1395–1402. doi:10.1016/j.apm.2007.06.008

    Article  MATH  MathSciNet  Google Scholar 

  8. Marro J, Torres JJ, Cortés JM (2007) Chaotic hopping between attractors in neural networks. Neural Netw 20(2):230–235. doi:10.1016/j.neunet.2006.11.005

    Article  MATH  Google Scholar 

  9. Liu X, Xiu C (2007) A novel hysteretic chaotic neural network and its applications. Neurocomputing 70(13–15):2561–2565. doi:10.1016/j.neucom.2007.02.002

    Article  Google Scholar 

  10. Bersini H, Sener P (2002) The connections between the frustrated chaos and the intermittency chaos in small Hopfield networks. Neural Netw 15(10):1197–1204. doi:10.1016/S0893-6080(02)00096-5

    Article  Google Scholar 

  11. Wang J, Chen L, Jing Z (2001) Chaos and asymptotical stability in discrete-time recurrent neural networks with generalized input–output function. Sci China Ser A Math 44(2). doi:10.1007/BF02874421

  12. Liao Z, Huang Y (2008) Horseshoe and topological entropy estimate of a class of three-dimensional cellular neural networks. Appl Math Comput 197(1):382–388. doi:10.1016/j.amc.2007.07.077

    Article  MATH  MathSciNet  Google Scholar 

  13. Li QD, Yang XS et al (2005) Hyperchaos in Hopfield-type neural networks. Neurocomputing 67:275–280. doi:10.1016/j.neucom.2005.02.009

    Article  Google Scholar 

  14. Yang X-S, Yuan Q (2005) Chaos and transient chaos in simple Hopfield neural networks. Neurocomputing 69:232–241. doi:10.1016/j.neucom.2005.06.005

    Article  Google Scholar 

  15. Yang X-S, Huang Y (2006) A new class of chaotic simple 3-neuron cellular neural network. Int J Bifurcat Chaos 16(4):1019–1021. doi:10.1142/S021812740601526X

    Article  MATH  MathSciNet  Google Scholar 

  16. Yang X-S, Li Q (2006) Horseshoe chaos in cellular neural networks. Int J Bifurcat Chaos 16(1). doi:10.1142/S0218127406014666 (in press)

  17. Hopfield JJ (1984) Neurons with graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci USA 81(10):3088–3092. doi:10.1073/pnas.81.10.3088

    Article  Google Scholar 

  18. Yang X-S, Tang Y (2004) Horseshoes in piecewise continuous maps. Chaos Solitons Fractals 19(4):841–845. doi:10.1016/S0960-0779(03)00202-9

    Article  MATH  MathSciNet  Google Scholar 

  19. Yang X-S, Li H-M, Huang Y (2005) A planar topological horseshoe theory with applications to computer verifications of chaos. J Phys Math Gen 38:4175–4185. doi:10.1088/0305-4470/38/19/008

    Article  MATH  MathSciNet  Google Scholar 

  20. Eckmann JP, Ruelle D (1985) Ergodic theory of chaos and strange attractors. Rev Mod Phys 57(3):617–656. doi:10.1103/RevModPhys.57.617

    Article  MathSciNet  Google Scholar 

  21. Wiggins S (1990) Introduction to applied nonlinear dynamical systems and chaos. Springer, New York

    MATH  Google Scholar 

  22. Robinson C (1995) Dynamical systems: stability, symbolic dynamics, and chaos. CRC Press, Boca Raton

    MATH  Google Scholar 

Download references

Acknowledgments

The research was funded by National Science Foundation of China (60875009) and the great project of Hubei Provincial Department of Education (Z20081301). The authors are very grateful to the reviewer for the valuable comments and suggestions.

Author information

Authors and Affiliations

  1. Institute of Intelligent Vision and Image Information, China Three Gorges University, 443002, Yichang, People’s Republic of China

    Zhiping Dan

  2. College of Electrical Engineering and Information Technology, China Three Gorges University, 443002, Yichang, People’s Republic of China

    Zhiping Dan

  3. School of Computer Science and Engineering, Wuhan Institute of Technology, 430073, Wuhan, People’s Republic of China

    Wen zhi Huang

  4. Department of Mathematics, Huazhong University of Science and Technology, 430074, Wuhan, People’s Republic of China

    Yan Huang

Authors
  1. Zhiping Dan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wen zhi Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yan Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhiping Dan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dan, Z., Huang, W.z. & Huang, Y. Chaos and rigorous verification of horseshoes in a class of Hopfield neural networks. Neural Comput & Applic 19, 159–166 (2010). https://doi.org/10.1007/s00521-009-0269-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-009-0269-8

Keywords

Search

Navigation