Output recurrent wavelet neural network-based adaptive backstepping controller for a class of MIMO nonlinear non-affine uncertain systems

Abstract

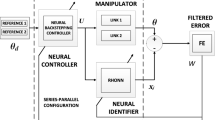
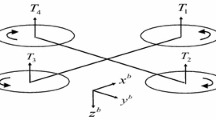
In this paper, an adaptive backstepping control problem is proposed for a class of multiple-input-multiple-output nonlinear non-affine uncertain systems. An output recurrent wavelet neural network (ORWNN) is used to approximate the unknown nonlinear functions to develop the proposed adaptive backstepping controller. The proposed ORWNN combines the advantages of wavelet-based neural network, fuzzy neural network, and output feedback layer to achieve higher approximation accuracy and faster convergence. According to the estimation of ORWNN, the control scheme is designed by backstepping approach such that the system outputs follow the desired trajectories. Based on the Lyapunov approach, our approach guarantees that the system outputs converge to a small neighborhood of the references signals, that is, all signals of the closed-loop system are semi-globally uniformly ultimately bounded. Finally, simulation results including double pendulums system and two inverted pendulums on carts system are shown to demonstrate the performance and effectiveness of our approach.

Appendix: Proof of Theorem 1

Before proving Theorem 1, the following Lemma 1 should be introduced.

Lemma 1 [8]

Let $V:[0,\infty ) \to \Re$ satisfy the inequality

$$ V(t) \le - 2\beta V + M,\forall t \ge 0 $$

(41)

where $\beta$ and M are positive constants. Then,

$$ V(t) \le V(t_{0} )\exp [ - 2\beta (t - t_{0} )] + \frac{M}{2\beta },\forall t \ge t_{0} . $$

(42)

Proof of Theorem 1

Design the Lyapunov candidate function

$$ V_{2} (t) = V_{1} (t) + \frac{1}{2}{\mathbf{e}}_{2}^{T} (t){\mathbf{e}}_{2} (t) + \frac{1}{{2r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{{\mathbf{T}}} {\tilde{\mathbf{w}}}) + \frac{1}{{2r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} {\tilde{\mathbf{m}}}) \, + \frac{1}{{2r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} {\tilde{\mathbf{\sigma }}}) + \frac{1}{{2r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} ) $$

(43)

where tr(.) denotes the trace of matrix. Differentiating (43), then, we have

$$ \begin{aligned} \dot{V}_{2} (t) & = \dot{V}_{1} (t) + {\mathbf{e}}_{2}^{T} (t){\dot{\mathbf{e}}}_{2} (t) - \frac{1}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} \dot{\hat{{{\mathbf w}}}}) - \frac{1}{{r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} \dot{\hat{{{\mathbf m}}}}) - \frac{1}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} \dot{\hat{{{\mathbf \sigma}}}}) - \frac{1}{{r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} \dot{\hat{{{\mathbf \theta}}}}_{{\mathbf{r}}} ) \\ & = - k_{1} {\mathbf{e}}_{1}^{T} (t){\mathbf{e}}_{1} (t) + {\mathbf{e}}_{1}^{T} (t){\mathbf{e}}_{2} (t) \, + {\mathbf{e}}_{2}^{T} (t)({\mathbf{H}} + ( - {\hat{\mathbf{H}}} - {\mathbf{e}}_{1} - k_{2} {\mathbf{e}}_{2} + {\dot{\mathbf{\alpha }}}) - {\dot{\mathbf{\alpha }}}) \\ & \quad - \frac{1}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} \dot{\hat{{{\mathbf w}}}}) - \frac{1}{{r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} \dot{\hat{{{\mathbf m}}}}) - \frac{1}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} \dot{\hat{{{\mathbf \sigma}}}}) - \frac{1}{{r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\hat{{{\mathbf \theta}}}}_{{\mathbf{r}}} ). \\ \end{aligned} $$

(44)

Substituting (15) into (44), we obtain

$$ \begin{aligned} \dot{V}_{2} (t) & = - k_{1} {\mathbf{e}}_{1}^{T} (t){\mathbf{e}}_{1} (t) - k_{2} {\mathbf{e}}_{2}^{T} (t){\mathbf{e}}_{2} (t) + {\mathbf{e}}_{2}^{T} (t)[{\tilde{\mathbf{w}}}^{T} ({\hat{\mathbf{\Uppsi }}} - {\varvec{\Uppsi}}_{m}^{T} {\hat{\mathbf{m}}} - {\varvec{\Uppsi}}_{\sigma }^{T} {\hat{\mathbf{\sigma }}} - {\varvec{\Uppsi}}_{\theta }^{T} {\hat{\mathbf{\theta }}}_{{\mathbf{r}}} ) \\ & \quad + \hat{w}^{T} ({\varvec{\Uppsi}}_{m} {\tilde{\mathbf{m}}} + {\varvec{\Uppsi}}_{\sigma } {\tilde{\mathbf{\sigma }}} + {\varvec{\Uppsi}}_{{\theta_{r} }} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} ) + {\varvec{\Updelta}}] \\ & \quad - \frac{1}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\dot{{\hat{\mathbf w}}}}) - \frac{1}{{r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} \dot{\hat{{{\mathbf m}}}}) - \frac{1}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} \dot{\hat{{{\mathbf \sigma}}}}) \, - \frac{1}{{r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} \dot{\hat{{{\mathbf \theta}}}}_{{\mathbf{r}}} ). \\ \end{aligned} $$

(45)

Substitute parameter update laws (30)–(33) into (45), $\dot{V}_{2}$ is

$$ \begin{aligned} \dot{V}_{2} (t) & = - \sum\limits_{i = 1}^{2} {k_{i} {\mathbf{e}}_{i}^{T} (t)} {\mathbf{e}}_{i} (t) + \sum\limits_{i = 1}^{2} {{\mathbf{e}}_{i}^{T} (t)({\varvec{\Updelta}}_{i} (t))} + \frac{2}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\hat{\mathbf{w}}}) + \frac{2}{{r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} {\hat{\mathbf{m}}}) + \frac{2}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} {\hat{\mathbf{\sigma }}}) \\ & \quad + \frac{2}{{r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\hat{\mathbf{\theta }}}_{{\mathbf{r}}} ) + \frac{2}{{r_{2} }}{\text{tr}}[{\tilde{\mathbf{m}}}^{T} ({\mathbf{m}}^{ * } - {\tilde{\mathbf{m}}})] + \frac{2}{{r_{3} }}{\text{tr}}[{\tilde{\mathbf{\sigma }}}^{T} ({\varvec{\sigma}}^{ * } - {\tilde{\mathbf{\sigma }}})] \, + \frac{2}{{r_{4} }}{\text{tr}}[{\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} ({\varvec{\theta}}_{{\mathbf{r}}}^{*} - {\hat{\mathbf{\theta }}}_{{\mathbf{r}}} )] \\ \end{aligned} $$

(46)

where ${\varvec{\Updelta}}_{1} = 0, \, {\varvec{\Updelta}}_{2} = {\varvec{\Updelta}}$. The following inequality is used to prove the stability of system (1) [8]

$$ ab \le ka^{2} + \frac{{b^{2} }}{4k} ,\quad \forall k > 0. $$

(47)

Then, we can choose the following inequalities

$$ 2{\tilde{\mathbf{w}}}^{T} {\mathbf{w}}^{*} \le {\tilde{\mathbf{w}}}^{T} {\tilde{\mathbf{w}}} + {\mathbf{w}}^{*T} {\mathbf{w}}^{*} , $$

(48)

$$ 2{\tilde{\mathbf{m}}}^{T} {\mathbf{m}}^{*} \le {\tilde{\mathbf{m}}}^{T} {\tilde{\mathbf{m}}} + {\mathbf{m}}^{*T} {\mathbf{m}}^{*} , $$

(49)

$$ 2{\tilde{\mathbf{\sigma }}}^{T} {\varvec{\sigma}}^{*} \le {\tilde{\mathbf{\sigma }}}^{T} {\tilde{\mathbf{\sigma }}} + {\varvec{\sigma}}^{*T} {\varvec{\sigma}}^{*} , $$

(50)

$$ 2{\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{*} \le {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{{}} + {\varvec{\theta}}_{{\mathbf{r}}}^{*T} {\varvec{\theta}}_{{\mathbf{r}}}^{*} . $$

(51)

Subsequently, (39) can be rewritten as

$$ \begin{aligned} \dot{V}_{2} & \le - \sum\limits_{i = 1}^{2} {k_{i} {\mathbf{e}}_{i}^{T} } {\mathbf{e}}_{i} + \sum\limits_{i = 1}^{2} {{\mathbf{e}}_{i}^{T} ({\varvec{\Updelta}}_{i} )} + \frac{1}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\tilde{\mathbf{w}}}) + \frac{1}{{r_{1} }}{\text{tr}}({\mathbf{w}}^{ * T} {\mathbf{w}}^{ * } ) - \frac{2}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\tilde{\mathbf{w}}}) + \frac{1}{{r_{2} }}{\text{tr}}(\tilde{m}^{T} \tilde{m}) \\ & \quad + \frac{1}{{r_{2} }}{\text{tr}}(m^{ * T} m^{ * } ) - \frac{2}{{r_{2} }}{\text{tr}}(\tilde{m}^{T} m) + \frac{1}{{r_{3} }}{\text{tr}}(\tilde{\sigma }^{T} \tilde{\sigma }) + \frac{1}{{r_{3} }}{\text{tr}}({\varvec{\sigma}}^{ * T} {\varvec{\sigma}}^{ * } ) \, - \frac{2}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} {\tilde{\mathbf{\sigma }}}) \\ & \quad + \frac{1}{{r_{4} }}{\text{tr}}\left( {{\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} } \right) \, + \frac{1}{{r_{4} }}{\text{tr}}\left( {{\varvec{\theta}}_{{\mathbf{r}}}^{*T} {\varvec{\theta}}_{{\mathbf{r}}}^{ * } } \right) - \frac{2}{{r_{4} }}{\text{tr}}\left( {{\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} } \right) \\ & \le - \sum\limits_{i = 1}^{2} {k_{i} {\mathbf{e}}_{i}^{T} } {\mathbf{e}}_{i} + \sum\limits_{i = 1}^{2} {{\mathbf{e}}_{i}^{T} ({\varvec{\Updelta}}_{i} )} + \frac{{\Updelta_{i}^{T} {\varvec{\Updelta}}_{i} }}{{2k_{i} }} - \frac{{\Updelta_{i}^{T} {\varvec{\Updelta}}_{i} }}{{2k_{i} }} + \left( {\sum\limits_{i = 1}^{2} {k_{i} \frac{{{\mathbf{e}}_{i}^{T} {\mathbf{e}}_{i} }}{2}} - \sum\limits_{i = 1}^{2} {k_{i} \frac{{{\mathbf{e}}_{i}^{T} {\mathbf{e}}_{i} }}{{\mathbf{2}}}} } \right) \\ & \quad - \frac{1}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{{\mathbf{T}}} {\tilde{\mathbf{w}}}) + \frac{1}{{r_{1} }}{\text{tr}}({\mathbf{w}}^{ * T} {\mathbf{w}}^{ * } ) - \frac{1}{{r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} {\tilde{\mathbf{m}}}) + \frac{1}{{r_{2} }}{\text{tr}}\left( {{\mathbf{m}}^{ * T} {\mathbf{m}}^{ * } } \right) - \frac{1}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{{\mathbf{T}}} {\tilde{\mathbf{\sigma }}}) \\ & \quad + \frac{1}{{r_{3} }}{\text{tr}}\left( {{\varvec{\sigma}}^{ * T} {\varvec{\sigma}}^{ * } } \right) - \frac{1}{{r_{4} }}{\text{tr}}\left( {{\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} } \right) + \frac{1}{{r_{4} }}{\text{tr}}\left( {{\varvec{\theta}}_{{\mathbf{r}}}^{*T} {\varvec{\theta}}_{{\mathbf{r}}}^{*} } \right) \, \\ & \le - \frac{1}{2}\sum\limits_{i = 1}^{2} {k_{i} {\mathbf{e}}_{i}^{T} {\mathbf{e}}_{i} + \sum\limits_{i = 1}^{2} {\frac{{{\varvec{\Updelta}}_{i}^{T} {\varvec{\Updelta}}_{i} }}{{2k_{i} }}} } \, - \sum\limits_{i = 1}^{2} {\left[ {\left( {\sqrt {\frac{{k_{i} }}{2}} {\mathbf{e}}_{i} - \sqrt {\frac{1}{{2k_{i} }}} {\varvec{\Updelta}}_{i} } \right)^{T} \left( {\sqrt {\frac{{k_{i} }}{2}} {\mathbf{e}}_{i} (t) - \sqrt {\frac{1}{{2k_{i} }}} {\varvec{\Updelta}}_{i} (t)} \right)} \right]} \\ & \quad - \frac{1}{{2r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\tilde{\mathbf{w}}}) \, + \frac{1}{{r_{1} }}{\text{tr}}\left( {{\mathbf{w}}^{ * T} {\mathbf{w}}^{ * } } \right) - \frac{1}{{2r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} {\tilde{\mathbf{m}}}) + \frac{1}{{r_{2} }}{\text{tr}}({\mathbf{m}}^{ * T} {\mathbf{m}}^{ * } ) - \frac{1}{{2r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} {\tilde{\mathbf{\sigma }}}) \, \\ & \quad + \frac{1}{{r_{3} }}{\text{tr}}\left( {{\varvec{\sigma}}^{ * T} {\varvec{\sigma}}^{ * } } \right) - \frac{1}{{2r_{4} }}{\text{tr}}\left( {{\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} } \right) \, + \frac{1}{{r_{4} }}{\text{tr}}\left( {{\varvec{\theta}}_{{\mathbf{r}}}^{*T} {\varvec{\theta}}_{{\mathbf{r}}}^{T} } \right) \\ & \le - \frac{1}{2}\sum\limits_{i = 1}^{2} {{\mathbf{e}}_{i}^{T} {\mathbf{e}}} - \frac{1}{{2r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\tilde{\mathbf{w}}}) - \frac{1}{{2r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} {\tilde{\mathbf{m}}}) - \frac{1}{{2r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} {\tilde{\mathbf{\sigma }}}) - \frac{1}{{2r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} ) + G \\ & \quad \le - CV_{2} + G \, \\ \end{aligned} $$

(52)

where C = 0.5, $V_{2} = \sum\nolimits_{i = 1}^{2} {{\mathbf{e}}_{i}^{T} {\mathbf{e}}_{i} } + \frac{1}{{r_{1} }}{\text{tr}}({\tilde{\mathbf{w}}}^{T} {\tilde{\mathbf{w}}}) + \frac{1}{{r_{2} }}{\text{tr}}({\tilde{\mathbf{m}}}^{T} {\tilde{\mathbf{m}}}) + \frac{1}{{r_{3} }}{\text{tr}}({\tilde{\mathbf{\sigma }}}^{T} {\tilde{\mathbf{\sigma }}}) + \frac{1}{{r_{4} }}{\text{tr}}({\tilde{\mathbf{\theta }}}_{{\mathbf{r}}}^{T} {\tilde{\mathbf{\theta }}}_{{\mathbf{r}}} )$, $\, G = \frac{{\Updelta_{i}^{T} \Updelta_{i} }}{{2k_{i} }} + \frac{1}{{r_{1} }}{\text{tr}}({\mathbf{w}}^{ * T} {\mathbf{w}}^{*} ) + \frac{1}{{r_{2} }}{\text{tr}}({\mathbf{m}}^{ * T} {\mathbf{m}}^{*} ) + \frac{1}{{r_{3} }}{\text{tr}}({\varvec{\sigma}}^{ * T} {\varvec{\sigma}}^{*} ) + \frac{1}{{r_{4} }}{\text{tr}}({\varvec{\theta}}_{{\mathbf{r}}}^{*T} {\varvec{\theta}}_{{\mathbf{r}}}^{*} )$. Hence, we have

$$ V_{2} (t) \le - CV_{2} (t) + G,\quad \forall t \ge 0. $$

(53)

By the literature of [8], we have

$$ e^{2Ct} \dot{V}_{2} (t) + 2Ce^{2Ct} V_{2} (t) \le e^{2Ct} G, $$

(54)

therefore,

$$ \frac{d}{dt}[e^{2Ct} \dot{V}_{2} (t)] \le e^{2Ct} G. $$

(55)

Integrating this inequality form $t_{0}$ to t yields

$$ e^{2Ct} \dot{V}_{2} (t) - e^{{2Ct_{0} }} \dot{V}_{2} (t_{0} ) \le \frac{G}{2C}(e^{2Ct} - e^{{2Ct_{0} }} ) \le \frac{G}{2C}e^{2Ct} . $$

(56)

Hence,

$$ V_{2} (t) \le V_{2} (t_{0} )\exp [ - 2C(t - t_{0} )] + \frac{G}{2C}. $$

(57)

It can imply that all the signals of the closed-loop system ${\mathbf{e}}_{1} (t), \, {\mathbf{e}}_{2} ( {\text{t), }}{\tilde{\mathbf{w}}}, \, {\tilde{\mathbf{m}}}, \, {\tilde{\mathbf{\sigma }}}, \, {\varvec{\theta}}_{{\mathbf{r}}} , { }$ converge to a bounded boundary as t → ∞. Consider system (1) and the adaptive laws (30)–(33), all the signals of the resulting closed-loop system are globally uniformly ultimately bounded (UUB) according to Lemma 1. Therefore, the stability proof is completely. □