Tracking in scale quad-rotors through adaptive augmentation

Abstract

This paper illustrates the application of an adaptive flight control architecture to a scale quad-rotor. For autonomous vertical takeoff and landing flight, it is common to separate the control problem into an inner fast loop that controls attitude and an outer slow loop that controls the trajectory tracking. In this paper, we augment a conventional proportional and derivative controller conceived mainly for hovering, with an adaptive element using a real-time tuning single hidden layer neural network in a inner–outer loop combined architecture to account for model inversion error cancelation, issued in the feedback linearization process. The results shown in simulations reveal the superior performance of the augmented controller in tracking maneuvers.

Appendix

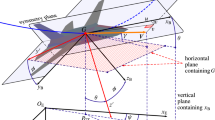
This section details the transformations associated with operations involving quaternions and rotation matrices. We shall adopt as the basis of the transformations the rotation matrix known as E ₁₂₃ and as quaternion structure q = {q ₀, q ₁, q ₂, q ₃}. Defining

$${\hbox {Roll}}[\phi] = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 &{\mathsf{c}}\phi & {\mathsf{s}}\phi \\ 0 & -{\mathsf{s}}\phi & {\mathsf{c}}\phi \\ \end{array} \right)$$

(65)

$${\hbox {Pitch}}[\theta] = \left( \begin{array}{ccc} {\mathsf{c}}\theta & 0 &-{\mathsf{s}}\theta \\ 0 & 1 & 0 \\ {\mathsf{s}}\theta & 0 & {\mathsf{c}}\theta \\ \end{array} \right)$$

(66)

$${\hbox {Yaw}}[\psi] = \left( \begin{array}{ccc} {\mathsf{c}}\psi &{\mathsf{s}}\psi & 0 \\ -{\mathsf{s}}\psi & {\mathsf{c}}\psi & 0 \\ 0 & 0 & 1 \\ \end{array} \right)$$

(67)

Thus $E_{123} = {\hbox {Roll}}[\phi]\cdot {\hbox {Pitch}}[\theta]\cdot {\hbox {Yaw}}[\psi].$ So the rotation matrix is

$$\left( \begin{array}{ccc} {\mathsf{c}}\theta {\mathsf{c}}\psi & {\mathsf{c}}\theta {\mathsf{s}}\psi & -{\mathsf{s}}\theta \\ {\mathsf{c}}\psi {\mathsf{s}}\theta {\mathsf{s}}\phi-{\mathsf{c}}\phi {\mathsf{s}}\psi \; & {\mathsf{c}}\phi {\mathsf{c}}\psi+{\mathsf{s}}\theta {\mathsf{s}}\phi {\mathsf{s}}\psi & {\mathsf{c}}\theta {\mathsf{s}}\phi \\ {\mathsf{c}}\phi {\mathsf{c}}\psi {\mathsf{s}}\theta+{\mathsf{s}}\phi {\mathsf{s}}\psi & {\mathsf{c}}\phi {\mathsf{s}}\theta {\mathsf{s}}\psi-{\mathsf{c}}\psi {\mathsf{s}}\phi & {\mathsf{c}}\theta {\mathsf{c}}\phi \\ \end{array} \right)$$

(68)

The quaternion product of p and q gives

$$p\cdot q = \left\{ \begin{array}{c} p_0 q_0-p_1 q_1-p_2 q_2-p_3q_3 \\ p_0 q_1+p_1 q_0+p_2 q_3-p_3q_2 \\ p_0 q_2-p_1 q_3+p_2 q_0+p_3 q_1 \\ p_0 q_3+p_1 q_2-p_2q_1+p_3 q_0 \end{array} \right\}^{\top}$$

(69)

For unitary quaternions, q ⁻¹ = {q ₀,  − q ₁,  − q ₂,  − q ₃ } so

$$q \oplus p = p\cdot q = \left\{ \begin{array}{c} p_0 q_0-p_1 q_1-p_2 q_2-p_3 q_3 \\ p_0 q_1+p_1 q_0+p_2 q_3-p_3q_2 \\ p_0 q_2-p_1 q_3+p_2 q_0+p_3 q_1\\ p_0 q_3+p_1 q_2-p_2q_1+p_3 q_0 \end{array} \right\}^{\top}$$

(70)

$$q\ominus p = p^{-1}\cdot q =\left\{ \begin{array}{c} p_0 q_0+p_1 q_1+p_2 q_2+p_3 q_3 \\ p_0 q_1-p_1 q_0-p_2 q_3+p_3 q_2 \\ p_0 q_2+p_1 q_3-p_2 q_0-p_3 q_1 \\ p_0 q_3-p_1 q_2+p_2q_1-p_3 q_0 \end{array} \right\}^{\top}$$

(71)

The conversion transformations between E ₁₂₃(ϕ, θ, ψ) and q are

$$\left\{ \begin{array}{c} {\mathsf{s}} \left(\frac{\theta }{2}\right) {\mathsf{s}} \left(\frac{\psi }{2}\right) {\mathsf{s}} \left(\frac{\phi }{2}\right)+{\mathsf{c}} \left(\frac{\theta }{2}\right) {\mathsf{c}} \left(\frac{\psi }{2}\right) {\mathsf{c}} \left(\frac{\phi }{2}\right)\\ {\mathsf{c}} \left(\frac{\theta }{2}\right) {\mathsf{c}} \left(\frac{\psi }{2}\right) {\mathsf{s}} \left(\frac{\phi }{2}\right)-{\mathsf{s}} \left(\frac{\theta }{2}\right) {\mathsf{s}} \left(\frac{\psi }{2}\right) {\mathsf{c}} \left(\frac{\phi }{2}\right)\\ {\mathsf{s}}\left(\frac{\theta }{2}\right) {\mathsf{c}} \left(\frac{\psi }{2}\right) {\mathsf{c}} \left(\frac{\phi }{2}\right)+{\mathsf{c}} \left(\frac{\theta }{2}\right) {\mathsf{s}} \left(\frac{\psi }{2}\right) {\mathsf{s}} \left(\frac{\phi }{2}\right)\\ {\mathsf{c}} \left(\frac{\theta }{2}\right) {\mathsf{s}} \left(\frac{\psi }{2}\right) {\mathsf{c}} \left(\frac{\phi }{2}\right)-{\mathsf{s}} \left(\frac{\theta }{2}\right) {\mathsf{c}} \left(\frac{\psi }{2}\right) {\mathsf{s}} \left(\frac{\phi }{2}\right) \end{array} \right\}^{\top}$$

(72)

and the inverse $q \longrightarrow E_{123}$

$$\begin{array}{l} \{\phi,\theta,\psi\} = \\ \left\{\begin{array}{c} \tan ^{-1}\left(q_0^2-q_1^2-q_2^2+q_3^2,2 (q_0 q_1+q_2 q_3)\right)\\ -\sin ^{-1}(2 (q_1 q_3-q_0 q_2)) \\ \tan ^{-1}\left(q_0^2+q_1^2-q_2^2-q_3^2,2 (q_0 q_3+q_1 q_2)\right) \end{array}\right\}^{\top} \end{array}$$

(73)

Also, the rotation matrix associated to a quaternion p is

$$\begin{array}{ccc} {\hbox {Rot}}[p] = \left( \begin{array}{lll} \scriptstyle p_0^2+p_1^2-p_2^2-p_3^2 &\scriptstyle 2 (p_1 p_2+p_0 p_3) & \scriptstyle 2 p_1 p_3-2 p_0 p_2 \\ \scriptstyle 2 p_1 p_2-2 p_0 p_3 & \scriptstyle p_0^2-p_1^2+p_2^2-p_3^2 & \scriptstyle 2 (p_0 p_1+p_2 p_3) \\ \scriptstyle 2 (p_0 p_2+p_1 p_3) & \scriptstyle 2 p_2 p_3-2 p_0 p_1 & \scriptstyle p_0^2-p_1^2-p_2^2+p_3^2 \\ \end{array} \right) \end{array}$$

(74)