Skip to main content

Advertisement

SpringerLink
Log in

A class of time-fractional-order continuous population models for interacting species with stability analysis

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

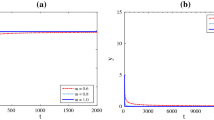
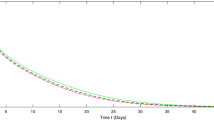
In recent years, prey–predator models appearing in various fields of mathematical biology have been proposed and studied extensively due to their universal existence and importance. The paper presents the solutions of time-fractional Lotka–Volterra models with the help of analytical method of nonlinear problem called homotopy perturbation method (HPM). By using initial values, the explicit solutions of time-fractional prey and predator populations for different particular cases have been derived. The numerical solutions show that only a few iterations are needed to obtain accurate approximate solutions. The dynamic behavior of the system investigated from the point of view of local stability. We also carry out a detailed analysis on stability of equilibrium.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. He JH (1999) Homotopy perturbation technique. Comput Methods Appl Mech Eng 178:257–262

    Article  Google Scholar 

  2. He JH (2000) A Coupling method of homotopy technique and perturbation technique for nonlinear problem. Int J Nonlinear Mech 35(1):37–43

    Article  Google Scholar 

  3. He JH (2004) Comparison of homotopy perturbation method and homotopy analysis method. Appl Math Comput 156:527–539

    Article  MathSciNet  Google Scholar 

  4. Yan LM (2013) Modified homotopy perturbation method coupled with Laplace transform for fractional heat transfer and porous media equations. Therm Sci 17(5):1409–1414

    Article  Google Scholar 

  5. He JH (2006) New interpretation of homotopy perturbation method. Int J Mod Phys B 20:2561–2568

    Article  Google Scholar 

  6. He JH (2006) Some asymptotic methods for strongly nonlinear equations. Int J Mod Phys B 20:1141–1199

    Article  Google Scholar 

  7. Saadatmandia A, Dehghan M, Eftekharia A (2009) Application of He’s homotopy perturbation method for non-linear system of second-order boundary value problems. Nonlinear Anal Real World Appl 10:1912–1922

    Article  MathSciNet  Google Scholar 

  8. Shakeri F, Dehghan M (2007) Numerical solution of a biological population model using He’s variational iteration method. Comput Math Appl 54:1197–1209

    Article  MathSciNet  Google Scholar 

  9. Dehghan M, Nasri M, Razvan MR (2007) Global stability of a deterministic model for HIV infection in vivo. Chaos, Solitons Fractals 34:1225–1238

    Article  MathSciNet  Google Scholar 

  10. Shakeri F, Dehghan M (2008) Solution of a model describing biological species living together using the variational iteration method. Math Comput Model 48:685–699

    Article  MathSciNet  Google Scholar 

  11. Dehghan M, Salehi R (2010) Solution of a nonlinear time-delay model in biology via semi-analytical approaches. Comput Phys Commun 181:1255–1265

    Article  MathSciNet  Google Scholar 

  12. Shakeri F, Dehghan M (2011) The finite volume spectral element method to solve Turing models in the biological pattern formation. Comput Math Appl 2:4322–4336

    Article  MathSciNet  Google Scholar 

  13. Pamuk S, Pamuk N (2010) He’s homotopy perturbation method for continuous population models for single and interacting species. Comput Math Appl 59:612–621

    Article  MathSciNet  Google Scholar 

  14. Hassan HN, El-Tawil MA (2012) Series solution for continuous population models for single and interacting species by the homotopy analysis method. Commun Numer Anal cna-00106:21

    MathSciNet  Google Scholar 

  15. Rafei M, Ganji DD, Danili H (2007) Solution of the epidemic model by homotopy perturbation method. Appl Math Comput 187:1056–1062

    Article  MathSciNet  Google Scholar 

  16. Podlubny I (1999) Fractional differential equation. Academic Press, New York

    Google Scholar 

  17. Samko SG, Kilbas AA, Marichev OI (2002) Fractional integrals and derivatives: theory and applications. Taylor and Francis, London

    Google Scholar 

  18. Murray JD (1993) Mathematical biology I. An introduction. Springer, Berlin

    Google Scholar 

  19. He JH (2014) A tutorial review on fractal space time and fractional calculus. Int J Theor Phys 53(11):3698–3718

    Article  Google Scholar 

  20. Saha Ray S (2008) An application of the modified decomposition method for the solution of coupled Klein–Gordon–Schrödinger equation. Commun Nonlinear Sci Numer Simul 13(7):1311–1317

    Article  MathSciNet  Google Scholar 

  21. Jafari H, Ghasempour S, Khalique CM (2013) A comparison between adomian’s polynomials and He’s polynomials for nonlinear functional equations. Math Probl Eng 943232:4

    Google Scholar 

  22. Jafari H, Ghasempour S, Khalique CM (2013) Comments on “He’s homotopy perturbation method for calculating Adomian polynomials”. Int J Nonlinear Sci Numer Simul 14(6):339–343

    Article  Google Scholar 

  23. Cai L, Li X, Ghosh M, Guo B (2009) Stability analysis of an HIV/AIDS epidemic model with treatment. J Comput Appl Math 229:313–323

    Article  MathSciNet  Google Scholar 

  24. Driessche PV, Watmough J (2002) Reproducing numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48

    Article  MathSciNet  Google Scholar 

  25. Das S, Gupta PK (2011) A mathematical model on fractional Lotka–Volterra equations. J Thoer Biol 277:1–6

    Article  MathSciNet  Google Scholar 

  26. Kuttler C (2009) Mathematical models in biology II. http://www-m6.ma.tum.de/~kuttler/script_current.pdf

Download references

Acknowledgments

This research work was financially supported by BRNS of Bhabha Atomic Research Centre, Mumbai under Department of Atomic Energy, Government of India vide Grant No. 2012/37P/54/BRNS/2382.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Rourkela, 769008, India

    S. Saha Ray & S. Sahoo

Authors
  1. S. Saha Ray
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Sahoo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Saha Ray.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saha Ray, S., Sahoo, S. A class of time-fractional-order continuous population models for interacting species with stability analysis. Neural Comput & Applic 26, 1495–1504 (2015). https://doi.org/10.1007/s00521-014-1816-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-014-1816-5

Keywords

Search

Navigation