NMF with local constraint and Deep NMF with temporal dependencies constraint for action recognition

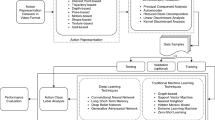
Abstract

In order to improve action recognition accuracy, a new nonnegative matrix factorization with local constraint (LC-NMF) is firstly presented. By applying it for effective trajectory clustering, complex backgrounds are removed and then the motion salient regions are obtained. Secondly, a nonnegative matrix factorization with temporal dependencies constraint (TD-NMF) is proposed, which fully mines the spatiotemporal relationship in a video not only between adjacent frames, but also between multi-interval frames. Meanwhile, the introduction of $l_{2,1}$-norm makes the spatiotemporal features possess better sparseness and robustness. In addition, these features are directly learned from data and thus have an inherent generalization ability. Finally, a Deep NMF method is established, which takes the proposed TD-NMF as the unit algorithm of each layer. By introducing the hierarchical feature extraction strategy, the base matrix of the first layer is gradually decomposed; then, it is supplemented and completed layer by layer. Consequently, the more complete and accurate local feature estimations are obtained, and then the discriminative and expressive abilities of features are effectively enhanced and recognition performance is further improved. Adequate and extensive experiments verify the effectiveness of the proposed methods. Moreover, the update rules and convergence proofs for LC-NMF and TD-NMF are also given.

Appendices

Appendix 1: Proof of Theorem 1

To prove Theorem 1, it is necessary to show that the objective function in Eq. (6) is non-increasing under the update rules in Eqs. (11) and (18). The objective function is firstly proved to be non-increasing under the update rule in Eq. (11) in this paper and then is demonstrated to be non-increasing under the update rule in Eq. (18). The proof procedure will utilize an auxiliary function which is similar to that employed in the EM algorithm.

Definition 1

If the conditions $G\left( {M,M^{\left( t \right)} } \right) \ge J\left( M \right)$ and $G\left( {M,M} \right) = J\left( M \right)$ are satisfied, then $G\left( {M,M^{\left( t \right)} } \right)$ is an auxiliary function of $J\left( M \right)$.

Lemma 1

If$G\left( {M,M^{\left( t \right)} } \right)$is an auxiliary function of$J\left( M \right)$, then$J\left( M \right)$is non-increasing under the following update rule:

$$ M^{{\left( {t + 1} \right)}} = {\text{argmin}}_{M} G\left( {M,M^{\left( t \right)} } \right) $$

(38)

Proof

$J\left( {M^{{\left( {t + 1} \right)}} } \right) \le G\left( {M^{{\left( {t + 1} \right)}} ,M^{\left( t \right)} } \right) \le G\left( {M^{\left( t \right)} ,M^{\left( t \right)} } \right) = J\left( {M^{\left( t \right)} } \right) .$

Now, the following will show that the update rule for ${\varvec{H}}$ in Eq. (6) is exactly the update rule in Eq. (11) with a suitable auxiliary function.

Considering any element $h_{kj}$ in ${\varvec{H}}$, $J_{kj}$ is used to represent the part of Eq. (6), which is only related to $h_{kj}$. It is easy to check that:

$$ J^{\prime}_{kj} = \left( {\frac{{\partial D_{\text{LC - NMF}} }}{{\partial {\varvec{H}}}}} \right)_{kj} = \left( { - 2{\varvec{F}}^{T} {\varvec{X}} + 2{\varvec{F}}^{T} {\varvec{FH}} + 2\lambda {\varvec{R}} \odot {\varvec{H}} \odot {\varvec{R}}} \right)_{kj} $$

(39)

$$ J^{\prime\prime}_{kj} = 2\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + 2\lambda \left( {{\varvec{R}} \odot {\varvec{R}}} \right)_{kj} $$

(40)

Since the update rule is element-wise in essence, it is sufficient to demonstrate that each $J_{kj}$ is non-increasing under the update rule of Eq. (6).

Lemma 2

Function (41) is an auxiliary function for$J_{kj}$, which is the part of$D_{{LC{ - }NMF}}$and only related to$h_{kj}$.

$$ G\left( {h,h_{kj}^{\left( t \right)} } \right) = J_{kj} \left( {h_{kj}^{\left( t \right)} } \right) + J^{\prime}_{kj} \left( {h_{kj}^{\left( t \right)} } \right)\left( {h - h_{kj}^{\left( t \right)} } \right) + \frac{{\left( {{\varvec{F}}^{T} {\varvec{FH}}} \right)_{kj} + \lambda \left( {{\varvec{R}} \odot {\varvec{H}} \odot {\varvec{R}}} \right)_{kj} }}{{h_{kj}^{\left( t \right)} }}\left( {h - h_{kj}^{\left( t \right)} } \right)^{2} $$

(41)

Proof

Since $G\left( {h,h} \right) = J_{kj} \left( h \right)$ is obvious, it only needs to prove that $G\left( {h,h_{kj}^{\left( t \right)} } \right) \ge J_{kj} \left( h \right)$. To do this, we make a comparison of the Taylor series expansion of $J_{kj} \left( h \right)$ with Eq. (41):

$$ J_{kj} \left( h \right) = J_{kj} \left( {h_{kj}^{\left( t \right)} } \right) + J^{\prime}_{kj} \left( {h_{kj}^{\left( t \right)} } \right)\left( {h - h_{kj}^{\left( t \right)} } \right) + \left[ {\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + \lambda \left( {{\varvec{R}} \odot {\varvec{R}}} \right)_{kj} } \right]\left( {h - h_{kj}^{\left( t \right)} } \right)^{2} $$

(42)

and it can be found that: $G\left( {h,h_{kj}^{\left( t \right)} } \right) \ge J_{kj} \left( h \right)$ is equivalent to

$$ \frac{{\left( {{\varvec{F}}^{T} {\varvec{FH}}} \right)_{kj} + \lambda \left( {{\varvec{R}} \odot {\varvec{H}} \odot {\varvec{R}}} \right)_{kj} }}{{h_{kj}^{\left( t \right)} }} \ge \left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + \lambda \left( {{\varvec{R}} \odot {\varvec{R}}} \right)_{kj} $$

(43)

Meanwhile, the following equations hold:

$$ \left( {{\varvec{F}}^{T} {\varvec{FH}}} \right)_{kj} = \sum\limits_{a} {\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{ka} h_{aj}^{\left( t \right)} \ge } \left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} h_{kj}^{\left( t \right)} $$

(44)

$$ \lambda \left( {{\varvec{R}} \odot {\varvec{H}} \odot {\varvec{R}}} \right)_{kj} = \lambda \left( {{\varvec{R}} \odot {\varvec{R}}} \right)_{kj} h_{kj}^{\left( t \right)} $$

(45)

Thus, Eq. (43) holds and $G\left( {h,h_{kj}^{\left( t \right)} } \right) \ge J_{kj} \left( h \right)$.

Now, it can be demonstrated that the objective function of Theorem 1 is non-increasing under the update rule in Eq. (11).

Proof

Replace $G\left( {h,h_{kj}^{\left( t \right)} } \right)$ in Eq. (38) by Eq. (41), and the following update rule can be obtained:

$$ \begin{aligned} h_{kj}^{{\left( {t + 1} \right)}} & = h_{kj}^{\left( t \right)} - h_{kj}^{\left( t \right)} \frac{{J^{\prime}_{kj} \left( {h_{kj}^{\left( t \right)} } \right)}}{{2\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + 2\lambda \left( {{\varvec{R}} \odot {\varvec{H}} \odot {\varvec{R}}} \right)_{kj} }} \\ & = h_{kj}^{\left( t \right)} \frac{{\left( {{\varvec{F}}^{T} {\varvec{X}}} \right)_{kj} }}{{\left( {{\varvec{F}}^{T} {\varvec{FH}} + \lambda {\varvec{R}} \odot {\varvec{H}} \odot {\varvec{R}}} \right)_{kj} }} \\ \end{aligned} $$

(46)

Since Eq. (41) is an auxiliary function, $J_{kj}$ is non-increasing under this update rule.

In the following, the objective function is proved to be non-increasing under the update rule in Eq. (18).

Considering any element $f_{ik}$ in ${\varvec{F}}$, $J_{ik}$ is used to represent the part of Eq. (6), which is only related to $f_{ik}$. It is easy to check that:

$$ J^{\prime}_{ik} = \left( {\frac{{\partial D_{\text{LC - NMF}} }}{{\partial {\varvec{F}}}}} \right)_{ik} = \left( { - 2{\varvec{XH}}^{T} + 2{\varvec{FHH}}^{T} + 4{\varvec{FF}}^{T} {\varvec{F}} - 4{\varvec{F}} + \lambda {\varvec{Q}}} \right)_{ik} $$

(47)

$$ J^{\prime\prime}_{ik} = 2\left( {{\varvec{HH}}^{T} } \right)_{kk} + 4\left( {\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + f_{ii}^{2} - 1} \right) + \lambda \left( {\frac{{\partial {\varvec{Q}}}}{{\partial {\varvec{F}}}}} \right)_{ik} $$

(48)

Lemma 3

Function (49) is an auxiliary function for$J_{ik}$, which is the part of$D_{\text{LC - NMF}}$and only related to$f_{ik}$.

$$ G\left( {f,f_{ik}^{\left( t \right)} } \right) = J_{ik} \left( {f_{ik}^{\left( t \right)} } \right) + J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)\left( {f - f_{ik}^{\left( t \right)} } \right) + \frac{{2\left( {{\varvec{FHH}}^{T} } \right)_{ik} + 4\left( {{\varvec{FF}}^{T} {\varvec{F}}} \right)_{ik} + \lambda \left( {\varvec{Q}} \right)_{ik} }}{{2f_{ik}^{\left( t \right)} }}\left( {f - f_{ik}^{\left( t \right)} } \right)^{2} $$

(49)

Proof

Since $G\left( {f,f} \right) = J_{ik} \left( f \right)$ is obvious, it only needs to show that $G\left( {f,f_{ik}^{\left( t \right)} } \right) \ge J_{ik} \left( f \right)$. To do this, we make a comparison of the Taylor series expansion of $J_{ik} \left( f \right)$ with Eq. (49):

$$ J_{ik} \left( f \right) = J_{ik} \left( {f_{ik}^{\left( t \right)} } \right) + J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)\left( {f - f_{ik}^{\left( t \right)} } \right) + \frac{1}{2}\left[ {2\left( {{\varvec{HH}}^{T} } \right)_{kk} + 4\left( {\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + f_{ii}^{2} - 1} \right) + \lambda \left( {\frac{{\partial {\varvec{Q}}}}{{\partial {\varvec{F}}}}} \right)_{ik} } \right]\left( {f - f_{ik}^{\left( t \right)} } \right)^{2} $$

(50)

Due to the condition $\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} { = }1$, $J_{ik} \left( f \right)$ can be rewritten as:

$$ J_{ik} \left( f \right) = J_{ik} \left( {f_{ik}^{\left( t \right)} } \right) + J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)\left( {f - f_{ik}^{\left( t \right)} } \right) + \frac{1}{2}\left[ {2\left( {{\varvec{HH}}^{T} } \right)_{kk} + 4f_{ii}^{2} + \lambda \left( {\frac{{\partial {\varvec{Q}}}}{{\partial {\varvec{F}}}}} \right)_{ik} } \right]\left( {f - f_{ik}^{\left( t \right)} } \right)^{2} $$

(51)

and it can be found that: $G\left( {f,f_{ik}^{\left( t \right)} } \right) \ge J_{ik} \left( f \right)$ is equivalent to

$$ \frac{{2\left( {{\varvec{FHH}}^{T} } \right)_{ik} + 4\left( {{\varvec{FF}}^{T} {\varvec{F}}} \right)_{ik} + \lambda \left( {\varvec{Q}} \right)_{ik} }}{{f_{ik}^{\left( t \right)} }} \ge 2\left( {{\varvec{HH}}^{T} } \right)_{kk} +\,4f_{ii}^{2} + \lambda \left( {\frac{{\partial {\varvec{Q}}}}{{\partial {\varvec{F}}}}} \right)_{ik} $$

(52)

Meanwhile, the following equations hold:

$$ \left( {{\varvec{FHH}}^{T} } \right)_{ik} = \sum\limits_{a} {f_{ia} \left( {{\varvec{HH}}^{T} } \right)_{ak} \ge } f_{ik} \left( {{\varvec{HH}}^{T} } \right)_{kk} $$

(53)

$$ \begin{aligned} \left( {{\varvec{FF}}^{T} {\varvec{F}}} \right)_{ik} & = \sum\limits_{a} {f_{ia} \left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{ak} \ge } f_{ii} \left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{ik} \\ & \ge f_{ii} \left( {\sum\limits_{a} {f_{ai} f_{ak} } } \right) \ge f_{ii} f_{ii} f_{ik} = f_{ii}^{2} f_{ik} \\ \end{aligned} $$

(54)

$$ \left( {\varvec{Q}} \right)_{ik} \ge f_{ik} \frac{{\partial \left( {\varvec{Q}} \right)_{ik} }}{{\partial f_{ik} }} $$

(55)

Thus, Eq. (52) holds and $G\left( {f,f_{ik}^{\left( t \right)} } \right) \ge J_{ik} \left( f \right)$.

Now, the objective function of Theorem 1 can also be demonstrated to be non-increasing under the update rule in Eq. (18).

Proof

Replace $G\left( {f,f_{ik}^{\left( t \right)} } \right)$ in Eq. (38) by Eq. (49), and the following update rule can be obtained:

$$ \begin{aligned} f_{ik}^{{\left( {t + 1} \right)}} & = f_{ik}^{\left( t \right)} - f_{ik}^{\left( t \right)} \frac{{J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)}}{{\left( {2{\varvec{FHH}}^{T} + 4{\varvec{FF}}^{T} {\varvec{F}} + \lambda {\varvec{Q}}} \right)_{ik} }} \\ & = f_{ik}^{\left( t \right)} \frac{{\left( {2{\varvec{XH}}^{T} + 4{\varvec{F}}} \right)_{ik} }}{{\left( {2{\varvec{FHH}}^{T} + 4{\varvec{FF}}^{T} {\varvec{F}} + \lambda {\varvec{Q}}} \right)_{ik} }} \\ \end{aligned} $$

(56)

Since Eq. (49) is an auxiliary function, $J_{ik}$ is non-increasing under this update rule. Thus, Theorem 1 holds.

Appendix 2: Proof of Theorem 2

To prove Theorem 2, it is necessary to show that objective function in Eq. (24) is non-increasing under the update rules in Eqs. (32) and (33). The objective function is firstly proved to be non-increasing under the update rule in Eq. (32) and then is also demonstrated to be non-increasing under the update rule in Eq. (33). The proof will utilize an auxiliary function which is similar to that employed in the EM algorithm.

According to the Definition 1 and Lemma 1 in “Appendix 1,” it can be proved that the objective function of Theorem 2 is non-increasing under the update rule in Eq. (32).

Considering any element $f_{ik}$ in ${\varvec{F}}$, $J_{ik}$ is utilized to represent the part of Eq. (24), which is only related to $f_{ik}$. It is easy to check that:

$$ \begin{aligned} J^{\prime}_{ik} & = \left( {\frac{{\partial D_{\text{TD - NMF}} }}{{\partial {\varvec{F}}}}} \right)_{ik} = \left( { - 2{\varvec{XH}}^{T} + 2{\varvec{FHH}}^{T} + 2\alpha \left( { - {\varvec{XH}}^{T} + {\varvec{XX}}^{T} {\varvec{F}}} \right)} \right)_{ik} \\ & \quad + \left( {2\alpha \sum\limits_{u \in U} {{\varvec{X}}\left( {{\varvec{P}}_{u}^{{\varvec{ + }}} {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} } \right){\varvec{X}}^{T} {\varvec{F}}{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} } \right)_{ik} \\ \end{aligned} $$

(57)

$$ \begin{aligned} J^{\prime\prime}_{ik} & = 2\left( {{\varvec{HH}}^{T} } \right)_{kk} + 2\alpha \left( {{\varvec{XX}}^{T} } \right)_{ii} \\ & \quad + 2\alpha \sum\limits_{u \in U} {\left( {{\varvec{X}}\left( {{\varvec{P}}_{u}^{{\varvec{ + }}} {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} } \right){\varvec{X}}^{T} } \right)_{ii} \left( {{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} \right)}_{kk} \\ \end{aligned} $$

(58)

Lemma 4

Function (59) is an auxiliary function for$J_{ik}$, which is the part of$D_{\text{TD - NMF}}$, and only related to$f_{ik}$.

$$ G\left( {f,f_{ik}^{\left( t \right)} } \right) = J_{ik} \left( {f_{ik}^{\left( t \right)} } \right) + J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)\left( {f - f_{ik}^{\left( t \right)} } \right) + \frac{{\left( {{\varvec{FHH}}^{T} + \alpha {\varvec{XX}}^{T} {\varvec{F}}} \right)_{ik} + \alpha {\varvec{Sum1}}}}{{f_{ik}^{\left( t \right)} }}\left( {f - f_{ik}^{\left( t \right)} } \right)^{2} $$

(59)

where${\varvec{Sum1}} = \sum\nolimits_{u \in U} {\left( {{\varvec{X}}\left( {{\varvec{P}}_{u}^{{\varvec{ + }}} {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} } \right){\varvec{X}}^{T} {\varvec{F}}{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} \right)_{ik} }$.

Proof

Since $G\left( {f,f} \right) = J_{ik} \left( f \right)$ is obvious, it only needs to show that $G\left( {f,f_{ik}^{\left( t \right)} } \right) \ge J_{ik} \left( f \right)$. To do this, we make a comparison of the Taylor series expansion of $J_{ik} \left( f \right)$ with Eq. (59),

$$ J_{ik} \left( f \right) = J_{ik} \left( {f_{ik}^{\left( t \right)} } \right) + J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)\left( {f - f_{ik}^{\left( t \right)} } \right) + \left[ {\left( {{\varvec{HH}}^{T} } \right)_{kk} + \alpha \left( {{\varvec{XX}}^{T} } \right)_{ii} + \alpha {\varvec{Sum2}}} \right]\left( {f - f_{ik}^{\left( t \right)} } \right)^{2} $$

(60)

where ${\varvec{Sum2}} = \sum\limits_{u \in U} {\left( {{\varvec{X}}\left( {{\varvec{P}}_{u}^{{\varvec{ + }}} {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} } \right){\varvec{X}}^{T} } \right)_{ii} \left( {{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} \right)}_{kk}$.

And it can be found that: $G\left( {f,f_{ik}^{\left( t \right)} } \right) \ge J_{ik} \left( f \right)$ is equivalent to

$$ \frac{{\left( {{\varvec{FHH}}^{T} + \alpha {\varvec{XX}}^{T} {\varvec{F}}} \right)_{ik} + \alpha {\varvec{Sum1}}}}{{f_{ik}^{\left( t \right)} }} \ge \left( {{\varvec{HH}}^{T} } \right)_{kk} + \alpha \left( {{\varvec{XX}}^{T} } \right)_{ii} + \alpha {\varvec{Sum2}} $$

(61)

Meanwhile, the following inequalities hold:

$$ \left( {{\varvec{FHH}}^{T} } \right)_{ik} = \sum\limits_{a} {f_{ia} } \left( {{\varvec{HH}}^{T} } \right)_{ak} \ge f_{ik}^{(t)} \left( {{\varvec{HH}}^{T} } \right)_{kk} $$

(62)

$$ \alpha \left( {{\varvec{XX}}^{T} {\varvec{F}}} \right)_{ik} = \alpha \sum\limits_{a} {\left( {{\varvec{XX}}^{T} } \right)_{ia} } f_{ak} \ge \alpha \left( {{\varvec{XX}}^{T} } \right)_{ii} f_{ik}^{\left( t \right)} $$

(63)

$$ \begin{aligned} {\varvec{Sum1}} & = \sum\limits_{a} {\sum\limits_{u \in U} {\left( {{\varvec{X}}\left( {{\varvec{P}}_{u}^{{\varvec{ + }}} {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} } \right){\varvec{X}}^{T} {\varvec{F}}} \right)_{ia} \left( {{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} \right)_{ak} } } \\ & \ge f_{ik}^{\left( t \right)} \sum\limits_{u \in U} {\left( {{\varvec{X}}\left( {{\varvec{P}}_{u}^{{\varvec{ + }}} {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} - {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} } \right){\varvec{X}}^{T} } \right)_{ii} \left( {{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} \right)_{kk} } \\ \end{aligned} $$

(64)

Thus, Eq. (61) holds and $G\left( {f,f_{ik}^{\left( t \right)} } \right) \ge J_{ik} \left( f \right)$.

Now, the objective function of Theorem 2 can be demonstrated to be non-increasing under the update rule in Eq. (32).

Proof

Replace $G\left( {f,f_{ik}^{\left( t \right)} } \right)$ in Eq. (38) by Eq. (59), and the following update rule can be obtained:

$$ \begin{aligned} f_{ik}^{{\left( {t + 1} \right)}} & = f_{ik}^{\left( t \right)} - f_{ik}^{\left( t \right)} \frac{{J^{\prime}_{ik} \left( {f_{ik}^{\left( t \right)} } \right)}}{{2\left( {\left( {{\varvec{FHH}}^{T} + \alpha {\varvec{XX}}^{T} {\varvec{F}}} \right)_{ik} + \alpha {\varvec{Sum1}}} \right)}} \\ & = f_{ik}^{\left( t \right)} \frac{{\left( {{\varvec{XH}}^{T} + \alpha {\varvec{XH}}^{T} + \sum\nolimits_{u \in U} {\alpha {\varvec{X}}\left( {{\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ - T} } \right){\varvec{X}}^{T} {\varvec{F}}{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} } \right)_{ik} }}{{\left( {{\varvec{FHH}}^{T} + \alpha {\varvec{XX}}^{T} {\varvec{F}} + \sum\nolimits_{u \in U} {\alpha {\varvec{X}}\left( {{\varvec{P}}_{u}^{ + } {\varvec{P}}_{u}^{ + T} + {\varvec{P}}_{u}^{ - } {\varvec{P}}_{u}^{ - T} } \right){\varvec{X}}^{T} {\varvec{F}}{\text{diag}}\left( {{\varvec{w}}_{u} } \right)^{T} {\text{diag}}\left( {{\varvec{w}}_{u} } \right)} } \right)_{ik} }} \\ \end{aligned} $$

(65)

Since Eq. (59) is an auxiliary function, $J_{ik}$ is non-increasing under this update rule.

In the following, the objective function is proved to be non-increasing under the update rule in Eq. (33).

Considering any element $h_{kj}$ in ${\varvec{H}}$, $J_{ik}$ is used to represent the part of Eq. (24), which is only related to $h_{kj}$. It is easy to check that:

$$ J^{\prime}_{kj} = \left( {\frac{{\partial D_{\text{TD - NMF}} }}{{\partial {\varvec{H}}}}} \right)_{kj} = \left( { - 2{\varvec{F}}^{T} {\varvec{X}} + 2{\varvec{F}}^{T} {\varvec{FH}} + 2\alpha \left( { - {\varvec{F}}^{T} {\varvec{X}} + {\varvec{H}}} \right) + \eta {\varvec{EH}}} \right)_{kj} $$

(66)

$$ J^{\prime\prime}_{kj} = 2\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + 2\alpha + \eta \left( {\varvec{E}} \right)_{kk} $$

(67)

Lemma 5

Function (68) is an auxiliary function for$J_{kj}$, which is the part of$D_{\text{TD - NMF}}$and only related to$h_{kj}$.

$$ G\left( {h,h_{kj}^{\left( t \right)} } \right) = J_{kj} \left( {h_{kj}^{\left( t \right)} } \right) + J^{\prime}_{kj} \left( {h_{kj}^{\left( t \right)} } \right)\left( {h - h_{kj}^{\left( t \right)} } \right) + \frac{{\left( {2{\varvec{F}}^{T} {\varvec{FH}} + 2\alpha {\varvec{H}} + \eta {\varvec{EH}}} \right)_{kj} }}{{2h_{kj}^{\left( t \right)} }}\left( {h - h_{kj}^{\left( t \right)} } \right)^{2} $$

(68)

Proof

Since $G\left( {h,h} \right) = J_{kj} \left( h \right)$ is obvious, it only needs to show that $G\left( {h,h_{kj}^{\left( t \right)} } \right) \ge J_{kj} \left( h \right)$. To do this, we make a comparison of the Taylor series expansion of $J_{kj} \left( h \right)$ with Eq. (68):

$$ J_{kj} \left( h \right) = J_{kj} \left( {h_{kj}^{\left( t \right)} } \right) + J^{\prime}_{kj} \left( {h_{kj}^{\left( t \right)} } \right)\left( {h - h_{kj}^{\left( t \right)} } \right) + \frac{1}{2}\left[ {2\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + 2\alpha + \eta \left( {\varvec{E}} \right)_{kk} } \right]\left( {h - h_{kj}^{\left( t \right)} } \right)^{2} $$

(69)

and it can be found that: $G\left( {h,h_{kj}^{\left( t \right)} } \right) \ge J_{kj} \left( h \right)$ is equivalent to

$$ \frac{{\left( {2{\varvec{F}}^{T} {\varvec{FH}} + 2\alpha {\varvec{H}} + \eta {\varvec{EH}}} \right)_{kj} }}{{h_{kj}^{\left( t \right)} }} \ge 2\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} + 2\alpha + \eta \left( {\varvec{E}} \right)_{kk} $$

(70)

Meanwhile, the following inequalities hold:

$$ 2\left( {{\varvec{F}}^{T} {\varvec{FH}}} \right)_{kj} = 2\sum\limits_{a} {\left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{ka} } h_{aj} \ge \left( {{\varvec{F}}^{T} {\varvec{F}}} \right)_{kk} h_{kj}^{\left( t \right)} $$

(71)

$$ \eta \left( {{\varvec{EH}}} \right)_{kj} = \eta \sum\limits_{a} {\left( {\varvec{E}} \right)_{ka} } h_{aj} \ge \eta \left( {\varvec{E}} \right)_{kk} h_{kj}^{\left( t \right)} $$

(72)

Thus, Eq. (70) holds and $G\left( {h,h_{kj}^{\left( t \right)} } \right) \ge J_{kj} \left( h \right)$.

Now, the objective function of Theorem 2 can also be demonstrated to be non-increasing under the update rule in Eq. (33).

Proof

Replace $G\left( {h,h_{kj}^{\left( t \right)} } \right)$ in Eq. (38) by Eq. (69), and the following update rule can be obtained:

$$ \begin{aligned} h_{kj}^{{\left( {t + 1} \right)}} & = h_{kj}^{\left( t \right)} - h_{kj}^{\left( t \right)} \frac{{J^{\prime}_{kj} \left( {h_{kj}^{\left( t \right)} } \right)}}{{\left( {2{\varvec{F}}^{T} {\varvec{FH}} + 2\alpha {\varvec{H}} + \eta {\varvec{EH}}} \right)_{kj} }} \\ & = h_{kj}^{\left( t \right)} \frac{{\left( {2{\varvec{F}}^{T} {\varvec{X}} + 2\alpha {\varvec{F}}^{T} {\varvec{X}}} \right)_{kj} }}{{\left( {2{\varvec{F}}^{T} {\varvec{FH}} + 2\alpha {\varvec{H}} + \eta {\varvec{{\rm E}{\rm H}}}} \right)_{kj} }} \\ \end{aligned} $$

(73)

Since Eq. (73) is an auxiliary function, $J_{kj}$ is non-increasing under this update rule. Thus, Theorem 2 holds.