Abstract
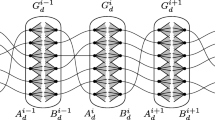
In this paper we consider the secret sharing problem on special access structures with minimal qualified subsets of size two, i.e. secret sharing on graphs. This means that the participants are the vertices of the graph and the qualified subsets are the subsets of V(G) spanning at least one edge. The information ratio of a graph G is denoted by R(G) and is defined as the ratio of the greatest size of the shares a vertex has to remember and of the size of the secret. Since the determination of the exact information ratio is a non-trivial problem even for small graphs (i.e. for V(G) = 6), every construction can be of particular interest. Let k be the maximal degree in G. In this paper we prove that R(G) = 2 − 1/k for every graph G with the following properties: (A) every vertex has at most one neighbour of degree one; (B) vertices of degree at least 3 are not connected by an edge; (C) the girth of the graph is at least 6. We prove this by using polyhedral combinatorics arguments and the entropy method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Beimel A, Livne N (2006) On matroids and non-ideal secret sharing, In: Proceedings of the third theory of cryptography conference. LNCS, vol 3876. pp 482–501
Blundo C, De Santis A, Stinson DR, Vaccaro U (1995) Graph decomposition and secret sharing schemes. J Crypt 8: 39–64
Blundo C, De Santis A, Simone RD, Vaccaro U (1997) Tight bounds on the information rate of secret sharing schemes. Des Codes Crypt 11: 107–122
Capocelli RM, De Santis A, Gargano L, Vaccaro U (1993) On the size of shares of secret sharing schemes. J Crypt 6: 157–168
Csirmaz L (1997) The size of a share must be large. J Crypt 10: 223–231
Csirmaz L (2007) Secret sharing schemes on graphs. Stud Math Hung 44: 297–306
Csirmaz L (2005) Secret sharing on the d-dimensional cube
Csirmaz L, Tardos G (2007) Exact bounds on tree based secret sharing schemes, Tatracrypt 2007, Slovakia
Csiszár I, Körner J (1981) Information theory. Coding theorems for discrete memoryless systems. Academic, New York
GNU Linear Programming Kit. http://www.gnu.org/software/glpk/
IACR Cryptology ePrint Archive. http://eprint.iacr.org/
Jackson W, Martin KM (1996) Perfect secret sharing schemes on five participants. Des Codes Crypt 9: 233–250
Library of Efficient Models and Optimization in Networks. http://lemon.cs.elte.hu
Martì-Farré J., Padró C. (2005) Secret sharing schemes with three or four minimal qualified subsets. Des Codes Crypt 34: 17–34
Matus F (1999) Matroid representations by partitions. Disc Math 203: 169–194
Shamir A (1979) How to share a secret. Commun ACM 22: 612–613
Stinson DR (1992) An explication of secret sharing schemes. Des Codes Crypt 2: 357–390
Stinson DR (1994) Decomposition construction for secret sharing schemes. IEEE Trans Inf Theory 40: 118–125
van Dijk M (1997) On the information rate of perfect secret sharing schemes. Des Codes Crypt 12: 143–169
van Dijk M, Kevenaar T, Schrijen GJ, Tuyls P (2006) Improved constructions of secret sharing schemes by applying (λ,ω)-decompositions. Inf Proc Lett 99: 154–157
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Csirmaz, L., Ligeti, P. On an infinite family of graphs with information ratio 2 − 1/k . Computing 85, 127–136 (2009). https://doi.org/10.1007/s00607-009-0039-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-009-0039-6