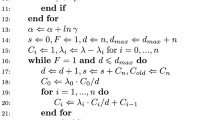Skip to main content
SpringerLink
Log in

On the smoothing of multinomial estimates using Liouville mixture models and applications

  • Theoretical Advances
  • Published:
Pattern Analysis and Applications Aims and scope Submit manuscript

Abstract

There has been major progress in recent years in statistical model-based pattern recognition, data mining and knowledge discovery. In particular, generative models are widely used and are very reliable in terms of overall performance. Success of these models hinges on their ability to construct a representation which captures the underlying statistical distribution of data. In this article, we focus on count data modeling. Indeed, this kind of data is naturally generated in many contexts and in different application domains. Usually, models based on the multinomial assumption are used in this case that may have several shortcomings, especially in the case of high-dimensional sparse data. We propose then a principled approach to smooth multinomials using a mixture of Beta-Liouville distributions which is learned to reflect and model prior beliefs about multinomial parameters, via both theoretical interpretations and experimental validations, we argue that the proposed smoothing model is general and flexible enough to allow accurate representation of count data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. The problem of data sparseness is also known as the zero-frequency problem [10].

  2. It is easy to note from Eq. 1 that the presence of zero counts creates serious numerical problems.

  3. Geometric interpretation of ∑ V v=1 α v has been proposed in [29].

  4. In particular the authors in [41] provide interesting discussions about the difference between Bayesian and empirical Bayesian approaches.

  5. Chang C-C, Lin C-J LIBSVM: a library for support vector machines. Available at http://www.csie.ntu.edu.tw/∼cjlin/libsv.

References

  1. Brodley CE, Smyth P (1997) Applying classification algorithms in practice. Stat Comput 7(1):45–56

    Article  Google Scholar 

  2. Bouguila N, Ziou D, Vaillancourt J (2003) Novel Mixture based on the Dirichlet distribution: application to data and image classification. In: Perner P, Rosenfeld A (eds) Machine learning and data mining in pattern recognition (MLDM). LNAI, vol 2734. Springer, Berlin, pp 172–181

  3. Vijaya PA, Murty MN, Subramanian DK (2006) Efficient median based clustering and classification techniques for protein sequences. Pattern Anal Appl 9(2-3):243–255

    Article  MathSciNet  Google Scholar 

  4. Dagan I, Lee L, Perrira FCN (1999) Similarity-based models of word cooccurrence probabilities. Mach Learn 34(1–3):43–69

    Article  MATH  Google Scholar 

  5. Scott S, Matwin S (1999) Feature engineering for text classification. In: Proceedings of the international conference on machine learning (ICML), pp 379–388

  6. Csurka G, Dance CR, Fan L, Willamowski J, Bray C (2004) Visual categorization with bags of keypoints. In: Workshop on statistical learning in computer vision, 8th European conference on computer vision (ECCV)

  7. Leung T, Malik J (2001) Representing and recognizing the visual appearance of materials using three-dimensional textons. Int J Comput Vis 43(1):29–44

    Article  MATH  Google Scholar 

  8. Bouguila N, ElGuebaly W (2009) Discrete data clustering using finite mixture models. Pattern Recognit 42(1):33–42

    Article  MATH  Google Scholar 

  9. Cheng BYM, Carbonell JG, Klein-Seetharaman J (2005) Protein classification based on text document classification techniques. Prot Struct Funct Bioinform 58:955–970

    Article  Google Scholar 

  10. Witten IH, Bell TC (1991) The zero-frequency problem: estimating the probabilities of novel events in adaptive text compression. IEEE Trans Inform Theory 37(4):1085–1094

    Article  Google Scholar 

  11. Fienberg SE, Holland PW (1973) Simultaneous estimation of multinomial cell probabilities. J Am Stat Assoc 68(343):683–691

    Article  MathSciNet  MATH  Google Scholar 

  12. Hall P, Titterington DM (1987) On smoothing sparse multinomial data. Aust J Stat 29(1):19–37

    Article  MathSciNet  MATH  Google Scholar 

  13. Simonoff JS (1995) Smoothing categorical data. J Stat Plann Infer 47:41–69

    Article  MathSciNet  MATH  Google Scholar 

  14. Bouguila N, Ziou D (2007) Unsupervised learning of a finite discrete mixture: applications to texture modeling and image databases summarization. J Vis Commun Image Represent 18(4):295–309

    Article  Google Scholar 

  15. Bouguila N, Ziou D (2004) A powerful finite mixture model based on the generalized Dirichlet distribution: unsupervised learning and applications. In Proceedings of the 17th international conference on pattern recognition (ICPR), pp 280–283

  16. Bouguila N, Ziou D (2004) Dirichlet-based probability model applied to human skin detection. In: IEEE international conference on acoustics, speech, and signal processing (ICASSP), pp 521–524

  17. Bouguila N, Ziou D, Hammoud RI (2009) On Bayesian analysis of a finite generalized Dirichlet mixture via a metropolis-within-Gibbs sampling. Pattern Anal Appl 12(2):151–166

    Article  MathSciNet  Google Scholar 

  18. McLachlan GJ, Peel D (2000) Finite mixture models. Wiley, New York

  19. Hoare Z (2008) Landscapes of Naive Bayes classifiers. Pattern Anal Appl 11(1):59–72

    Article  MathSciNet  Google Scholar 

  20. Andrés-Ferrer J, Juan A (2010) Constrained domain maximum likelihood estimation for Naive Bayes text classification. Pattern Anal Appl 13(2):189–196

    Article  MathSciNet  Google Scholar 

  21. Goodman LA (1970) The multivariate analysis of qualitative data: interactions among multiple classifications. J Am Stat Assoc 65(329):226–256

    Article  Google Scholar 

  22. Goodman LA (1971) The analysis of multidimensional contingency tables: stepwise procedures and direct estimation methods for building models for multiple classifications. Technometrics 13(1):33–61

    Article  MATH  Google Scholar 

  23. Goodman LA (1964) Interactions in multidimensional contingency tables. Ann Math Stat 35(2):632–646

    Article  MATH  Google Scholar 

  24. Gart JJ, Zweifel JR (1967) On the bias of various estimators of the logit and its variance with application to quantal bioassay. Biometrika 54(1/2):181–187

    Article  MathSciNet  MATH  Google Scholar 

  25. Grizzle JE, Starmer CF, Koch GG (1969) Analysis of categorical data by linear models. Biometrics 25(3):489–504

    Article  MathSciNet  MATH  Google Scholar 

  26. Bouguila N, Ziou D (2004) Improving content based image retrieval systems using finite multinomial Dirichlet mixture. In: Proceedings of the IEEE workshop on machine learning for signal processing (MLSP), pp 23–32

  27. Bouguila N (2007) Spatial color image databases summarization. In: IEEE International conference on acoustics, speech, and signal processing (ICASSP), vol 1, Honolulu, HI, USA, pp 953–956

  28. Good IJ, Bayesian A (1967) Significance test for multinomial distribution (with Discussion). J R Stat Soc B 29(3):399–431

    MATH  Google Scholar 

  29. Fienberg SE (1972) On the choice of flattening constants for estimating multinomial probabilities. J Multivar Anal 2(1):127–134

    Article  MathSciNet  Google Scholar 

  30. Lidstone GJ (1920) Note on the general case of the Bayes–Laplace formula for inductive or a posteriori probabilities. Trans Fac Actuar 8:182–192

    Google Scholar 

  31. Jeffreys J (1961) Theory of probability. 3rd edn. Clarendon Press, Oxford

    MATH  Google Scholar 

  32. Perks W (1947) Some observations on inverse probability including a new indifference rule (with discussion). J Inst Actuar 73:285–334

    MathSciNet  Google Scholar 

  33. Bouguila N, Ziou D, Vaillancourt J (2004) Unsupervised learning of a finite mixture model based on the Dirichlet distribution and its application. IEEE Trans Image Process 13(11):1533–1543

    Article  Google Scholar 

  34. Lochner RH (1975) A generalized Dirichlet distribution in Bayesian life testing. J R Stat Soc B 37:103–113

    MathSciNet  MATH  Google Scholar 

  35. Bouguila N, ElGuebaly W (2008) On discrete data clustering. In: Proceedings of the Pacific–Asia conference on knowledge discovery and data mining (PAKDD). LNCS, vol 5012. Springer, Osaka, pp 503–510

  36. Fang KT, Kotz S, Ng KW (1990) Symmetric multivariate and related distributions. Chapman and Hall, New York

  37. Bouguila N, Ziou D (2005) Using unsupervised learning of a finite Dirichlet mixture model to improve pattern recognition applications. Pattern Recognit Lett 26(12):1916–1925

    Article  Google Scholar 

  38. Bouguila N, Ziou D, Monga E (2006) Practical Bayesian estimation of a finite beta mixture through Gibbs sampling and its applications. Stat Comput 16(2):215–225

    Article  MathSciNet  Google Scholar 

  39. Robbins HE (1956) An empirical Bayes approach to statistics. In: Neyman J (ed) Proceedings of the third Berkeley symposium on mathematical statistics and probability, vol 1, pp 157–163

  40. Robbins HE (1964) The empirical Bayes approach to statistics. Ann Math Stat 35(1):1–20

    Article  MathSciNet  MATH  Google Scholar 

  41. Deely JJ, Lindley DV (1981) Bayes empirical Bayes. J Am Stat Assoc 76(376):833–841

    Article  MathSciNet  MATH  Google Scholar 

  42. Carlin BP, Louis TA (2000) Bayes and empirical Bayes methods for data analysis, 2nd edn. Chapman & Hall/CRC, Boca Raton

  43. McLachlan JG, Krishnan T (1997) The EM Algorithm and Extensions. Wiley

  44. Hu T, Sung SY (2005) Clustering spatial data with a hybrid EM approach. Pattern Anal Appl 8(1–2):139–148

    Article  MathSciNet  Google Scholar 

  45. Bouguila N, Ziou D (2007) High-dimensional unsupervised selection and estimation of a finite generalized Dirichlet mixture model based on minimum message length. IEEE Trans Pattern Anal Mach Intell 29(10):1716–1731

    Article  Google Scholar 

  46. Rissanen J (1978) Modeling by shortest data description. Automatica 14:465–471

    Article  MATH  Google Scholar 

  47. Dhillon IS, Modha DS (2001) Concept decompositions for large sparse text data using clustering. Mach Learn 42(1–2):143–175

    Article  MATH  Google Scholar 

  48. Lebanon G, Lafferty J (2004) Hyperplane margin classifiers on the multinomial manifold. In: Proceedings of the international conference on machine learning (ICML), pp 66–73

  49. Vapnik VN (1998) Statistical learning theory. Wiley, New York

    MATH  Google Scholar 

  50. Zhang D, Chen X, Lee WS (2005) Text classification with kernels on the multinomial manifold. In: Proceedings of the 28th annual international ACM SIGIR conference on research and development in information retrieval (SIGIR), pp 266–273

  51. Jebara T, Kondor R, Howard A (2004) Probability product kernels. J Mach Learn Res 5:819–844

    MathSciNet  MATH  Google Scholar 

  52. Moreno PJ, Ho PP, Vasconcelos N (2003) A Kullback–Leibler divergence based kernel for SVM classification in multimedia applications. In: Proceedimgs of advances in neural information processing systems (NIPS). MIT Press, Cambridge

  53. Topsoe F (2000) Some inequalities for information divergence and related measures of discrimination. IEEE Trans Inform Theory 46(4):1602–1609

    Article  MathSciNet  Google Scholar 

  54. Chapelle O, Haffner P, Vapnik VN (1999) Support vector machines for histogram-based image classification. IEEE Trans Neural Netw 10(5):1055–1064

    Article  Google Scholar 

  55. Varma M, Zisserman A (2002) Classifying images of materials: achieving viewpoint and illumination independence. In: Proceedings of the European conference on computer vision (ECCV), pp 255–271

  56. Szczypiński PM, Strzelecki M, Materka A, Klepaczko A (2009) MaZda: a software package for image texture analysis. Comput Methods Prog Biomed 94(1):66–76

    Article  Google Scholar 

  57. Zhu SC, Wu Y, Mumford D (1998) Filters, random fields and maximum entropy (FRAME): towards a unified theory for texture modeling. Int J Comput Vis 27(2):107–126

    Article  Google Scholar 

  58. Varma M, Zisserman A (2009) A statistical approach to material classification using image patch exemplars. IEEE Trans Pattern Anal Mach Intell 31(11):2032–2047

    Article  Google Scholar 

  59. Dana KJ, van Ginneken B, Nayar SK, Koenderink JJ (1999) Reflectance and texture of real-world surfaces. ACM Trans Graphics 18(1):1–34

    Article  Google Scholar 

  60. Lazebnik S, Schmid C, Ponce J (2005) A sparse texture representation using local affine regions. IEEE Trans Pattern Anal Mach Intell 27(8):1265–1278

    Article  Google Scholar 

  61. Grzegorzek M (2010) A system for 3D texture-based probabilistic object recognition and its applications. Pattern Anal Appl 13(3):333–348

    Article  MathSciNet  Google Scholar 

  62. Schiele B, Pentland A (1999) Probabilistic object recognition and localization. In: Proceedings of the IEEE international conference on computer vision (ICCV), pp 177–182

  63. Amsaleg L, Gros P (2001) Content-based retrieval using local descriptors: problems and issues from a database perspective. Pattern Anal Appl 4(2–3):108–124

    Article  MathSciNet  MATH  Google Scholar 

  64. Caputo B, Wallraven C, Nilsback M-E (2004) Object categorization via local kernels. In: Proceedings of the 17th international conference on pattern recognition (ICPR), pp 132–135

  65. Lyu S (2005) Mercer kernels for object recognition with local features. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 223–229

  66. Deselaers T, Keysers D, Ney H (2005) Discriminative training for object recognition using image patches. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 157–162

  67. Loupias E, Sebe N, Bres S, Jolion J (2000) Wavelet-based salient points for image retrieval. In: Proceedings of the IEEE international conference on image processing (ICIP), pp 518–521

  68. Linde Y, Buzo A, Gray RM (1980) An algorithm for vector quantization design. IEEE Trans Commun 28:84–95

    Article  Google Scholar 

  69. Nene SA, Nayar SK, Murase H (1996) Columbia object image library (COIL-20). Technical Report CUCS-005-96, Columbia University

  70. Nene SA, Nayar SK, Murase H (1996) Columbia object image library (COIL-100). Technical Report CUCS-006-96, Columbia University

  71. Weber M, Welling M, Perona P (2000) Unsupervised learning of object models and recognition. In: Proceedings of the European conference on computer vision (ECCV), pp 18–32

  72. Bouguila N, Ziou D (2010) A Dirichlet process mixture of generalized Dirichlet distributions for proportional data modeling. IEEE Trans Neural Netw 21(1):107–122

    Article  Google Scholar 

  73. Bouguila N (2009) A model-based approach for discrete data clustering and feature weighting using MAP and stochastic complexity. IEEE Trans Knowl Data Eng 21(12):1649–1664

    Article  Google Scholar 

Download references

Acknowledgments

The completion of this research was made possible thanks to the Natural Sciences and Engineering Research Council of Canada (NSERC).

Author information

Authors and Affiliations

  1. Concordia Institute for Information Systems Engineering (CIISE), Concordia University, Montreal, QC, H3G 1T7, Canada

    Nizar Bouguila

Authors
  1. Nizar Bouguila
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nizar Bouguila.

Appendices

Appendix 1: Proof of Eq. 23

We start by computing the posterior distribution:

$$\begin{aligned} p({\varvec {\pi}}|{\mathbf {X}},\Uptheta)& =\frac{p({\mathbf {X}},{\varvec {\pi}} |\Uptheta)}{p({\mathbf {X}}|\Uptheta)}\\ &=\frac{1}{\sum_{j=1}^M p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j)\Upgamma(\beta_j)} \frac{\Upgamma(\alpha_j^{\prime})\Upgamma(\beta_j^{\prime})}{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})\Upgamma(\alpha_j^{\prime}+\beta_j^{\prime})}}\\ &\quad \times \sum_{j=1}^M p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j)\Upgamma(\beta_j)}\\ &\quad \times \prod_{v=1}^{V-1} \frac{\pi_v^{\alpha_{jv}+X_v-1}}{\Upgamma(\alpha_{jv})} \left(\sum_{v=1}^{V-1} \pi_{v}\right)^{\alpha_j-\sum_{v=1}^{V-1} \alpha_{jv}}\\ &\quad \times \left(1-\sum_{v=1}^{V-1} \pi_v\right)^{\beta_j+X_V-1} \end{aligned}$$
(44)

To find the estimate of a certain parameter the \(\pi_l, l=1,\ldots,V\) when a Beta-Liouville mixture is taken as a prior, we have to compute the expectation π v according to the previous posterior distribution:

$$ \begin{aligned} \hat{\pi}_l&=\int\limits_{\pi_l}\pi_l p({\varvec {\pi}}|{\mathbf {X}},\Uptheta){\rm{d}}\pi_l\\ &=\frac{1}{\sum_{j=1}^M p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j) \Upgamma(\beta_j)\prod_{v=1}^{V-1}\Upgamma(\alpha_{jv})} \frac{\Upgamma(\alpha_j^{\prime})\Upgamma(\beta_j^{\prime})\prod_{v=1}^{V-1} \Upgamma(\alpha_{jv}^{\prime})}{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})\Upgamma(\alpha_j^{\prime}+\beta_j^{\prime})}}\\ &\quad\times \sum_{j=1}^M p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)} {\Upgamma(\alpha_j)\Upgamma(\beta_j)\prod_{v=1}^{V-1}\Upgamma(\alpha_{jv})}\\ & \quad\times \int\limits_{\pi_l}\left[\prod_{v=1}^{V-1}\pi_v^{\alpha_{jv}+\delta(v=l)+X_v-1}\right.\\ &\left.\left(\sum_{v=1}^{V-1} \pi_{v}\right)^{\alpha_j-\sum_{v=1}^{V-1} \alpha_{jv}}\left(1-\sum_{v=1}^{V-1} \pi_{v}\right)^{\beta_j+X_V-1}{\rm{d}}\pi_l\right]\\ =&\frac{1}{\sum_{j=1}^M p_j \frac{\Upgamma\left(\sum_{v=1}^{V-1} \alpha_{jv}\right)\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j) \Upgamma(\beta_j)\prod_{v=1}^{V-1}\Upgamma(\alpha_{jv})} \frac{\Upgamma(\alpha_j^{\prime})\Upgamma(\beta_j^{\prime})\prod_{v=1}^{V-1} \Upgamma(\alpha_{jv}^{\prime})}{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})\Upgamma(\alpha_j^{\prime}+\beta_j^{\prime})}}\\ &\quad\times \sum_{j=1}^M p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j) \Upgamma(\beta_j)\prod_{v=1}^{V-1}\Upgamma(\alpha_{jv})}\\ &\quad\times \frac{\Upgamma(\alpha_j^{\prime}+1)\Upgamma(\beta_j^{\prime}) \Upgamma(\alpha_{jl}^{\prime}+1)\prod_{v=1,v \neq l}^{V-1}\Upgamma(\alpha_{jv}^{\prime})}{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}+1)\Upgamma(\alpha_j^{\prime}+\beta_j^{\prime}+1)} \end{aligned} $$

where δ(v = l) = 1 if v = 1 and 0, otherwise. Since \(\Upgamma (x+1)=x \Upgamma(x),\) we obtain

$$ \hat{\pi}_l=\sum_{j=1}^M p(j|{\mathbf {X}}) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jl}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}} $$

where

$$ p(j|{\mathbf {X}})=\frac{p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j) \Upgamma(\beta_j)\prod_{v=1}^{V-1}\Upgamma(\alpha_{jv})} \frac{\Upgamma(\alpha_{j}^{\prime}) \Upgamma(\beta_{j}^{\prime})\prod_{v=1}^{V-1} \Upgamma(\alpha_{jv}^{\prime})}{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})\Upgamma(\alpha_j^{\prime}+\beta_j^{\prime})}} {\sum_{j=1}^M p_j \frac{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv})\Upgamma(\alpha_j+\beta_j)}{\Upgamma(\alpha_j) \Upgamma(\beta_j)\prod_{v=1}^{V-1}\Upgamma(\alpha_{jv})} \frac{\Upgamma(\alpha_{j}^{\prime})\Upgamma(\beta_{j}^{\prime}) \prod_{v=1}^{V-1}\Upgamma(\alpha_{jv}^{\prime})}{\Upgamma(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})\Upgamma(\alpha_{j}^{\prime}+\beta_{j}^{\prime})}} $$

Appendix 2: Proof of Eqs. 29, 30 and 31

We have

$$ \begin{aligned} \log &f({\mathcal{X}}|\Uptheta)\\ &\quad=\sum_{n=1}^N\left[{X_{nv}}\left(\sum_{v=1}^{V-1} \log\left(\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+ \beta_{j}^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right)\right.\\ &\left.\qquad+{X_{nV}} \log \left(1-\sum_{v=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right] \end{aligned} $$

Thus,

$$ \begin{aligned} &\frac{\partial \log f({\mathcal{X}}|\Uptheta)}{\partial \alpha_j}\\ &=\sum_{n=1}^{N}\left[{X_{nv}}\frac{\partial}{\partial \alpha_{j}}\left(\sum_{v=1}^{V-1} \hbox{log}\left(\sum_{j=1}^{M} p(j|{{\mathbf{X}}}_{n}) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right)\right.\\ &\quad+\left.{X_{nV}} \frac{\partial}{\partial \alpha_j}\hbox{log} \left(1-\sum_{v=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right]\\ &=\sum_{n=1}^N\left[{X_{nv}}\left(\sum_{v=1}^{V-1}\frac{\frac{\partial} {\partial \alpha_j} \left(\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right)\right.\\ &\quad +\left.{X_{nV}} \frac{\frac{\partial}{\partial \alpha_j}\left(1-\sum_{v=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{1-\sum_{l=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right]\\ &=\sum_{n=1}^N\left[{X_{nv}}\left(\sum_{v=1}^{V-1}F_{njv} \frac{\partial}{\partial \alpha_j}\hbox{log}( p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}})\right)\right.\\ &\quad\left.-{X_{nV}} \frac{\frac{\partial}{\partial \alpha_j}\left(\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{1-\sum_{l=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right]\\ &=\sum_{n=1}^N\left[{X_{nv}}\left(\sum_{v=1}^{V-1}F_{njv} \frac{\partial}{\partial \alpha_j}\hbox{log}(\frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+ \beta_{j}^{\prime}})\right)\right.\\ &\quad\left.-{X_{nV}} F_{njV}\frac{\partial}{\partial \alpha_j}\hbox{log}(\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}})\right]\\ &=\sum_{n=1}^N\left[{X_{nv}}\left(\sum_{v=1}^{V-1}F_{njv} \left(\frac{1}{\alpha_{j}^{\prime}}-\frac{1} {\alpha_{j}^{\prime}+\beta_{j}^{\prime}}\right)\right)\right.\\ &\quad\left.-{X_{nV}} F_{njV}\frac{\sum_{v=1}^{V-1} p(j|{{\mathbf{X}}}_n) \frac{\beta_{j}^{\prime}}{(\alpha_{j}^{\prime}+\beta_{j}^{\prime})^2} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}{\sum_{v=1}^{V-1} p(j|{{\mathbf{X}}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right]\\ \end{aligned} $$

where

$$ F_{njv}=\frac{p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}{\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}} $$
$$ F_{njV}=\frac{\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}{1-\sum_{v=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}} $$

Using the same development, we can easily show that

$$ \begin{aligned} \frac{\partial \log f({\mathcal{X}}|\Uptheta)}{\partial \beta_j}&=\sum_{n=1}^N\left[\vphantom{{X_{nV}} F_{njV}\frac{\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{(\alpha_j^{\prime}+\beta_j^{\prime})^2}\frac{\alpha_{jv}^{\prime}} {\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}{\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}}{X_{nv}}\left(\sum_{v=1}^{V-1}F_{njv}\left(-\frac{1}{\alpha_j^{\prime}+\beta_j^{\prime}}\right)\right)\right.\\ &\left.+{X_{nV}} F_{njV}\frac{\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{(\alpha_j^{\prime}+\beta_j^{\prime})^2}\frac{\alpha_{jv}^{\prime}} {\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}{\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_j^{\prime}}{\alpha_j^{\prime}+\beta_j^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right] \\ \end{aligned} $$

and that

$$ \begin{aligned} &\frac{\partial \log f({\mathcal{X}}|\Uptheta)}{\partial \alpha_{jv}}\\ &=\sum_{n=1}^N\left[{X_{nv}}\left(\frac{\frac{\partial}{\partial \alpha_{jv}} \left(\sum_{j=1}^M p(j|\mathbf{X}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{\sum_{j=1}^{M} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right)\right.\\ &\quad\left.+{X_{nV}}\frac{\frac{\partial}{\partial \alpha_{jv}}\left(1-\sum_{v=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{1-\sum_{l=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right]\\ &=\sum_{n=1}^N\left[\vphantom{-{X_{nV}} \frac{\frac{\partial}{\partial \alpha_{jv}}\left(\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{1-\sum_{l=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}}{X_{nv}}\left(F_{njv}\frac{\partial}{\partial {\alpha_{jv}}}\hbox{log}\left(p(j|{{\mathbf{X}}}_{n}) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+ \beta_{j}^{\prime}}\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right)\right. \\ &\quad\left.-{X_{nV}} \frac{\frac{\partial}{\partial \alpha_{jv}}\left(\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{1-\sum_{l=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right]\\ &=\sum_{n=1}^N\left[{X_{nv}}\left(F_{njv}\frac{\partial}{\partial \alpha_{jv}}\hbox{log}\left(\frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right)\right. \\ &\quad\left.-{X_{nV}} F_{njV}\frac{\partial}{\partial \alpha_{jv}} \hbox{log}\left(\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right] \\ &=\sum_{n=1}^N\left[\vphantom{-{X_{nV}} \frac{\frac{\partial}{\partial \alpha_{jv}}\left(\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)}{1-\sum_{l=1}^{V-1}\sum_{j=1}^M p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}}{X_{nv}}\left(F_{njv}\left(\frac{1}{\alpha_{jv}^{\prime}}-\frac{1}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}\right)\right)\right.\\ &\quad\left.-{X_{nV}} F_{njV}\frac{ p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})-\alpha_{jv}^{\prime}}{(\sum_{v=1}^{V-1} \alpha_{jv}^{\prime})^2}}{\sum_{v=1}^{V-1} p(j|{\mathbf {X}}_n) \frac{\alpha_{j}^{\prime}}{\alpha_{j}^{\prime}+\beta_{j}^{\prime}} \frac{\alpha_{jv}^{\prime}}{\sum_{v=1}^{V-1} \alpha_{jv}^{\prime}}}\right]\\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bouguila, N. On the smoothing of multinomial estimates using Liouville mixture models and applications. Pattern Anal Applic 16, 349–363 (2013). https://doi.org/10.1007/s10044-011-0236-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10044-011-0236-8

Keywords

Search

Navigation