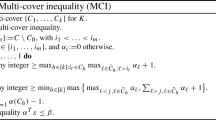Skip to main content

Advertisement

SpringerLink
Log in

Second-order cover inequalities

  • FULL LENGTH PAPER
  • Published:
Mathematical Programming Submit manuscript

Abstract

We introduce a new class of second-order cover inequalities whose members are generally stronger than the classical knapsack cover inequalities that are commonly used to enhance the performance of branch-and-cut methods for 0–1 integer programming problems. These inequalities result by focusing attention on a single knapsack constraint in addition to an inequality that bounds the sum of all variables, or in general, that bounds a linear form containing only the coefficients 0, 1, and –1. We provide an algorithm that generates all non-dominated second-order cover inequalities, making use of theorems on dominance relationships to bypass the examination of many dominated alternatives. Furthermore, we derive conditions under which these non-dominated second-order cover inequalities would be facets of the convex hull of feasible solutions to the parent constraints, and demonstrate how they can be lifted otherwise. Numerical examples of applying the algorithm disclose its ability to generate valid inequalities that are sometimes significantly stronger than those derived from traditional knapsack covers. Our results can also be extended to incorporate multiple choice inequalities that limit sums over disjoint subsets of variables to be at most one.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Balas E. (1975). Facets of the Knapsack Polytope. Math. Program. 8: 146–164

    Article  MATH  MathSciNet  Google Scholar 

  2. Crowder H.P., Johnson E.L. and Padberg M.W. (1983). Solving large-scale zero-one linear programming problems. Oper. Res. 31: 803–834

    MATH  Google Scholar 

  3. Geoffrion A.M. (1969). An improved implicit enumeration approach for integer programming. Oper. Res. 17: 437–454

    MATH  Google Scholar 

  4. Glover F. (1965). A multiphase-dual algorithm for the zero-one integer programming problem. Oper. Res. 13: 879–919

    MATH  MathSciNet  Google Scholar 

  5. Glover F. (1971). Flows in arborescences. Manage. Sci. 17: 568–586

    MathSciNet  MATH  Google Scholar 

  6. Glover F., Sherali H.D. and Lee Y. (1997). Generating cuts from surrogate constraint analysis for zero-one and multiple choice programming. Comput. Optim. Appl. 8(2): 152–172

    Article  MathSciNet  Google Scholar 

  7. Gu Z., Nemhauser G.L. and Savelsbergh M.W.P. (1998). Cover inequalities for 0–1 linear programs: computation. INFORMS J. Comput. 10: 427–437

    Article  MathSciNet  Google Scholar 

  8. Hammer P.L., Johnson E.L. and Peled U.N. (1975). Facets of regular 0–1 polytopes. Math. Program. 8: 179–206

    Article  MATH  MathSciNet  Google Scholar 

  9. Hanafi, S.: Contribution à la résolution de problèmes duaux de grande taille en optimisation combinatoire. Ph.D. Thesis, University of Valenciennes, France (1993)

  10. Hanafi, S., Glover, F.: Exploiting nested inequalities and surrogate constraints. Research Report, University of Valenciennes, France, and University of Colorado, Boulder, CO, USA (2005)

  11. Hooker, J.N.: Logic-based methods for optimization. In: Borning, A. (ed.) Principles and Practice of Constraint Programming. Lecture Notes in Computer Science, Vol. 874, pp. 336–349 (1994)

  12. Hooker J.N. and Osorio M.A. (1999). Mixed logical/linear programming. Discrete Appl. Math. 96–97: 395–442

    Article  MathSciNet  Google Scholar 

  13. Nemhauser G.L., Savelsbergh M.W.P. and Sigismondi G.S. (1994). MINTO, a mixed INTeger optimizer. Oper. Res. Lett. 15: 47–58

    Article  MATH  MathSciNet  Google Scholar 

  14. Nemhauser G.L. and Wolsey L.A. (1999). Integer and Combinatorial Optimization. 2nd edn. Wiley, New York

    MATH  Google Scholar 

  15. Osorio M.A., Glover F. and Hammer P. (2002). Cutting and surrogate constraint analysis for improved multidimensional knapsack solutions. Ann. Oper. Res. 117: 71–93

    Article  MATH  MathSciNet  Google Scholar 

  16. Savelsbergh M.W.P. (1994). Preprocessing and probing for mixed integer programming problems. ORSA J. Comput. 6: 445–454

    MATH  MathSciNet  Google Scholar 

  17. Sherali H.D. and Lee Y. (1995). Sequential and simultaneous liftings of minimal cover inequalities for generalized upper bound constrained knapsack polytopes. SIAM J. Discrete Math. 8(1): 133–153

    Article  MATH  MathSciNet  Google Scholar 

  18. Spielberg, K., Guignard, M.: A sequential (Quasi) hot start method for BB (0, 1) mixed integer programming. Mathematical Programming Symposium, Atlanta, GA (2000)

  19. Vasquez M. and Vimont Y. (2005). Improved results on the 0–1 multidimensional knapsack problem. Eur. J. Oper. Res. 165: 70–81

    Article  MATH  MathSciNet  Google Scholar 

  20. Wolsey L.A. (1975). Faces for a linear inequality in 0–1variables. Math. Program. 8: 165–178

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Colorado, Boulder, CO, 80309-0419, USA

    Fred Glover

  2. Grado Department of Industrial and Systems Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA, 24061, USA

    Hanif D. Sherali

Authors
  1. Fred Glover
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hanif D. Sherali
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fred Glover.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Glover, F., Sherali, H.D. Second-order cover inequalities. Math. Program. 114, 207–234 (2008). https://doi.org/10.1007/s10107-007-0098-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-007-0098-4

Keywords

Mathematics Subject Classification

Search

Navigation