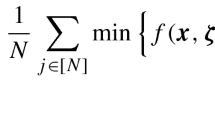On quantile cuts and their closure for chance constrained optimization problems

Abstract

A chance constrained optimization problem over a finite distribution involves a set of scenario constraints from which a small subset can be violated. We consider the setting where all scenario constraints are mixed-integer convex. Existing works typically consider a mixed integer nonlinear programming (MINLP) formulation of this problem by introducing binary variables to indicate which constraint systems are to be satisfied or violated. A variety of cutting plane approaches for this MINLP formulation have been developed. In this paper we consider a family of cuts in the original space rather than those in the extended space of the MINLP reformulation. These cuts, known as quantile cuts, can be viewed as a projection of the well known family of mixing inequalities for the MINLP reformulation onto the original problem space. We show that the closure of the infinite family of all quantile cuts has a finite description. An important corollary of this result is that for linear chance constrained problems the quantile closure is polyhedral. We further show that a recursive application of quantile closure operations recovers the convex hull of the nonconvex chance constrained set in the limit, and in the pure integer setting the convergence is finite. We show that separation of quantile cuts is in general NP-hard, develop a heuristic separation method, and demonstrate its effectiveness through a computational study. We also study an approximation of the quantile closure and propose a generalization by grouping scenarios.

1 Introduction

A chance constrained problem (CCP) involves optimization over constraints (specified by stochastic data) which are required to be satisfied with a prescribed probability level. A generic formulation of CCP is

$$\begin{aligned} \min _x \left\{ c^{\top }x : \ x \in S, \ {\mathbb {P}}[{\varvec{\xi }} : x \in {\mathcal X}({\varvec{\xi }})] \ge 1-\epsilon \right\} . \end{aligned}$$

(1)

In the above formulation, S denotes a set of deterministic constraints, ${\varvec{\xi }}$ denotes a random data vector, and ${\mathcal X}({\varvec{\xi }})$ denotes a system of stochastic constraints whose data is specified by the random vector ${\varvec{\xi }}$. The CCP (1) seeks a solution $x \in S$ that minimizes the cost $c^\top x$ and satisfies the stochastic constraints ${\mathcal X}({\varvec{\xi }})$ with probability at least $(1-\epsilon )$ where $\epsilon \in (0,1)$ is a prespecified risk level.

We consider a CCP with mixed integer convex constraints under finite distribution, i.e. we assume that

• $S=\{x\in {\mathbb R}^{n-\tau }\times {\mathbb {Z}}^\tau : G_0(x)\le 0\}$ is a nonempty and compact deterministic mixed integer set defined by the convex mapping $G_0:{\mathbb R}^n\rightarrow {\mathbb R}^{m_0}$;

• ${\varvec{\xi }}$ is a random vector with a finite distribution supported on $\Xi = \{\xi ^1,\ldots ,\xi ^N\}$, where each $\xi ^i$ for $i \in [N]:= \{1,\ldots ,N\}$ corresponds to a scenario with a probability mass $p_i$; and

• for a given scenario i, the vector $\xi ^i$ defines a nonempty and compact mixed convex integer constraint system ${\mathcal X}^i := {\mathcal X}(\xi ^i) =\{x\in {\mathbb R}^{n-\tau }\times {\mathbb {Z}}^\tau : G_i(x)\le 0\}$ defined by the convex mapping $G_i:{\mathbb R}^n\rightarrow {\mathbb R}^{m_i}$.

In this setting, the chance constraint in (1) corresponds to satisfying a subset $\mathcal {C} \subseteq [N]$ of the scenario constraints, i.e. $x \in \cap _{i \in \mathcal C} {\mathcal X}^i$, such that $\sum _{i \in \mathcal {C}} p_i \ge 1- \epsilon$ . Let

$$\begin{aligned} \mathcal {Z} := \left\{ \mathcal {C} \subseteq [N]: \ \sum _{i \in \mathcal {C}} p_i \ge 1-\epsilon \right\} , \end{aligned}$$

(2)

be the collection of all feasible subsets of scenarios. Then the feasible region of (1), denoted by X, can be written in the disjunctive normal form:

$$\begin{aligned} X=\bigcup _{{\mathcal C}\in \mathcal {Z}}\left[ S\bigcap _{i \in {\mathcal C}}{\mathcal X}^i\right] . \end{aligned}$$

(3)

We assume throughout that CCP is feasible, and hence X is nonempty. From the above disjunctive normal form it is clear that, even in the absence of integrality restrictions, i.e. $\tau = 0$, the set X is nonconvex, and not surprisingly CCP is strongly NP-hard [10, 12].

Since the sets ${\mathcal X}^i$ for all $i \in [N]$ are compact we can introduce binary variables $z_i$ for $i \in [N]$ and reformulate (1) as the mixed integer nonlinear program (MINLP):

$$\begin{aligned} \min _{x,z} \left\{ c^{\top }x : \ x \in S, \ G_i(x)\le M_i(1-z_i),\forall i\in [N], \ z \in Z \right\} , \end{aligned}$$

(4)

where

$$\begin{aligned} Z := \left\{ z \in \{0,1\}^N: \sum _{i \in [N]} p_i z_i \ge 1-\epsilon \right\} , \end{aligned}$$

and $M_i\in {\mathbb R}^{m_i}$ for all $i \in [N]$ are suitable big-M coefficients. Since the continuous relaxation of (4) is typically very weak, there has been a great deal of work in deriving strong valid inequalities for this MINLP. One popular approach is to derive a relaxation of (4) in the form of the well-studied mixing set [6] and add the corresponding mixing inequalities [1, 8,9,10, 18].

We consider a family of valid inequalities for the nonconvex feasible region X of the CCP (1) in the original x-space, rather than those for the MINLP formulation (4) in the (x, z)-space. These valid inequalities known as quantile cuts are obtained as follows. We first optimize a linear function $\alpha ^\top x$ over each scenario constraint, and record the optimal values $\beta _i^{\alpha } = \min \{\alpha ^\top x : x \in S \cap {\mathcal X}^i\}$ for $i \in [N]$. This approach and resulting $\beta _i^{\alpha }$ values was used in [9] to derive a mixing set relaxation for (4). Notice that each $\beta _i^{\alpha }$ has the associated probability $p_i$. Next we compute the $(1-\epsilon )$-quantile of $\{\beta _i^{\alpha }\}_{i \in [N] }$ based on these probabilities—denote this by $\beta ^{\alpha }_q$. The quantile cut is then given by $\alpha ^\top x \ge \beta ^{\alpha }_q$. Such inequalities were studied in [12] where it is shown that a single quantile cut represents the projection of the convex hull of a mixing set relaxation of (4) in the (x, z)-space onto the x space. Quantile cuts have been used in computational studies of chance constrained problems with good results [2, 12, 16].

In this paper we undertake a theoretical study of quantile cuts. In particular we study properties of the quantile closure, i.e. the intersection of all quantile cuts. Quantile cuts represent an infinite family of inequalities—one for each $\alpha$ vector—and so a finite description of the quantile closure and separation over it are important questions. By replacing the deterministic constraint system S in (1) with the (first) quantile closure we obtain a stronger formulation for which we can apply another round of quantile cuts and derive the second quantile closure and so on. We investigate how the sequence of sets produced by such successive quantile closure operations relates to the convex hull of the feasible region of (1). The main results of this paper are summarized below.

• 1. We show that the quantile closure has a finite description in conjunctive normal form. An important corollary of this result is that for a mixed integer linear CCP, the quantile closure is polyhedral.

• 2. We prove that the sequence of sets obtained by successive quantile closure operations converges to the convex hull of X (i.e., ${{\mathrm{conv}}}(X)$) with respect to the Hausdorff metric. In the pure integer linear setting, i.e. $\tau =n$, there exists a finite number of rounds of the quantile closure that recovers ${{\mathrm{conv}}}(X)$.

• 3. We study an approximation of the quantile closure given by a restricted choice of $\alpha$, and show finite convergence for mixed integer linear CCPs. We also study the approximation error for covering problems.

• 4. We study a generalization and strengthening quantile cuts and their closure obtained by grouping scenarios together.

• 5. We show that separation over the first quantile closure is NP-hard, and propose a heuristic separation algorithm. We present a computational study to show the effectiveness of heuristically separated quantile cuts.

The remainder of this paper is organized as follows. In Sect. 2 we discuss the connection of quantile cuts for ${{\mathrm{conv}}}(X)$ to the mixing set inequalities for the MINLP (4). In Sect. 3 we establish the conjunctive normal form of the quantile closures. In Sect. 4 we study convergence properties of successive quantile closures. An approximate quantile closure is studied in Sect. 5 followed by a generalization by grouping scenarios together in Sect. 6. In Sect. 7, we prove complexity of separation over the first quantile closure and propose a heuristic separation method. Numerical studies in Sect. 8 show that these quantile cuts indeed help reduce the root gap as well as the solution time. We provide some concluding remarks in Sect. 9.

2 Quantile cuts and mixing inequalities

We first formally define the quantile cut for the CCP (1). Recall that S is a set of deterministic constraints, ${\mathcal X}^i$ are constraints associated with scenario $i \in [N]$, $\mathcal {Z}$ defined in (2) is the collection of all feasible scenario sets, and X given by (3) is the set of feasible solutions of (1).

Definition 1

Given $\alpha \in {\mathbb R}^n$ let $\{\beta _i^\alpha (S)\}_{i\in [N]}$ be the optimal values of

$$\begin{aligned} \beta _i^\alpha (S)=\min \left\{ \alpha ^\top x: x\in S\cap {\mathcal X}^i\right\} \quad \forall i\in [N]. \end{aligned}$$

(5)

The quantile $\beta _{q}^\alpha (S)$ is given by

$$\begin{aligned} \beta _{q}^\alpha (S):&=\min _{{\mathcal C}\in \mathcal {Z}} \max _{i\in {\mathcal C}}\beta _i^\alpha (S) \end{aligned}$$

(6)

and the associated “quantile cut” is

$$\begin{aligned} \alpha ^\top x\ge \beta _{q}^\alpha (S).\end{aligned}$$

(7)

Note that the above definition depends on S so as to allow for successive applications with changing S. Since S and ${\mathcal X}^i$ are compact we have that $\beta _i^\alpha (S) \in (-\infty ,+\infty ]$ where the value of $+\infty$ is taken when the problem (5) is infeasible. When $p_i=\frac{1}{N}$ for all $i\in [N]$, we have that $\beta _{q}^\alpha (S)$ is the $(\lfloor \epsilon N\rfloor +1)$st largest value among $\{\beta _{i}^\alpha (S)\}_{i\in [N]}$.

From the definition above and the disjunctive normal form (3) of X it should be clear that the quantile cut (7) is valid for ${{\mathrm{conv}}}(X)$. We next reveal the connection between quantile cuts and mixing inequalities for CCP, which also establishes the validity of these cuts.

A mixing set [6] is a mixed-integer set of the form

$$\begin{aligned} P=\left\{ (v,z)\in {\mathbb R}_+\times \left\{ 0,1\right\} ^s: v+h_iz_i\ge h_i \ i=1,\ldots ,s\right\} \end{aligned}$$

(8)

with $h_1\ge \cdots \ge h_s$. The following exponential family of mixing inequalities are valid for P

$$\begin{aligned} v+\sum _{j=1}^l(h_{t_j}-h_{t_{j+1}})z_{t_j}\ge h_{t_1} \quad \forall \ T=\left\{ t_1,\ldots ,t_l\right\} \subseteq \left\{ 1,\ldots ,s\right\} , \end{aligned}$$

(9)

where $h_{t_1}\ge \cdots \ge h_{t_l},h_{t_{l+1}}=0$. These inequalities are facet defining for P when $t_1=1$ and are sufficient to describe the convex hull of P (see [3, 6]).

Using the $\beta$-values as defined in (5) Luedtke [9] constructed the following mixing set relaxation of CCP (4). Note that in [9] each scenario ${\mathcal X}^i$ is a polyhedron, however the construction directly extends to the MINLP formulation (4).

$$\begin{aligned} Y^\alpha =&\left\{ (x,z)\in {\mathbb R}^n\times \{0,1\}^N:\alpha ^\top x+(\beta _{i}^\alpha (S)-\beta _{q}^\alpha (S))(1-z_i)\ge \beta _{i}^\alpha (S),\right. \nonumber \\&\left. \ \ i\in \mathcal {B}_{q}^\alpha ,z\in Z\right\} . \end{aligned}$$

(10)

where $\mathcal {B}_{q}^\alpha :=\{i\in [N]:\beta _i^\alpha (S)\ge \beta _{q}^\alpha (S)\}$ is a subset of scenarios each of whose $\beta$-value is at least as large as the quantile $\beta _{q}^\alpha (S)$.

Proposition 1

(Theorem 1, [9]) For any $\alpha$, the system $Y^\alpha$ is a relaxation of the feasible region of the MINLP (4), and hence $X \subseteq {{\mathrm{Proj}}}_{x}(Y^{\alpha })$, where ${{\mathrm{Proj}}}_{x}(\cdot )$ denotes the projection of a set onto the x-space.

Note that $Y^\alpha$ is a mixing system with a knapsack side constraint defined by Z, thus the mixing inequalities of the form (9) are valid. These inequalities were used within a branch and cut scheme for solving the MINLP (4) in [9]. Note that the mixing inequalities are in the (x, z)-space while the quantile cuts are in the original x-space. The next result shows that a single quantile cut in the x-space captures the effect of the entire exponential family of mixing inequalities.

Proposition 2

(Proposition 5, [12]) For any $\alpha$,

$$\begin{aligned} {{\mathrm{Proj}}}_{x}({{\mathrm{conv}}}(Y^\alpha ))=\{x\in {\mathbb R}^n:\alpha ^\top x\ge \beta _{q}^\alpha (S)\}. \end{aligned}$$

Inspired by the above result we investigate, in the remainder of the paper, the strength of the quantile closure, i.e. the intersection of all quantile cuts.

3 Quantile closure

In this section we define quantile closures and establish their finite characterizations.

Definition 2

The first quantile closure of S is defined as

$$\begin{aligned} S^{1}:=\bigcap _{\begin{subarray}{c}\alpha \in {\mathbb R}^n \end{subarray}} \left\{ x\in {\mathbb R}^n: \alpha ^\top x\ge \beta _{q}^\alpha (S)\right\} . \end{aligned}$$

Inductively, we define rth round quantile closure $S^{r}$ as

$$\begin{aligned} S^{r}:=\bigcap _{\begin{subarray}{c}\alpha \in {\mathbb R}^n \end{subarray}} \left\{ x\in {\mathbb R}^n: \alpha ^\top x\ge \beta _{q}^\alpha (S^{r-1})\right\} \quad r\ge 2. \end{aligned}$$

Next we characterize ${{\mathrm{conv}}}(X)$ and $S^1$ in conjunctive normal form. Let us begin with the following definition.

Definition 3

A set $\mathbf {g}\subseteq [N]$ is a “partial covering subset” if it intersects with all of feasible scenario subsets in $\mathcal {Z}$, i.e., for any $\widehat{{\mathcal C}}\in \mathcal {Z}$, we have $\mathbf {g}\cap \widehat{{\mathcal C}}\ne \emptyset$. Also, a set $\mathbf {g}$ is a “minimal” partial covering subset if there does not exist another partial covering subset $\mathbf {g}'\subseteq [N]$ such that $\mathbf {g}'\subsetneq \mathbf {g}$. We let $\mathcal {G}$ denote the collection of all minimal partial covering subsets.

Note that when $p_i=\frac{1}{N}$ for all $i\in [N]$, then the collection of minimal partial covering subsets is $\mathcal {G}=\{\mathbf {g}\subseteq [N]: |\mathbf {g}|=\lfloor \epsilon N\rfloor +1\}$.

Proposition 3

$$\begin{aligned} X=\bigcap _{\mathbf {g}\in \mathcal {G}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right] . \end{aligned}$$

(11)

Proof

Define $X'=\bigcap _{\mathbf {g}\in \mathcal {G}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right]$. We need to show that $X=X'$.

Let $x\in X$. Then, there exists a feasible subset ${\mathcal C}\in \mathcal {Z}$ such that $x\in \bigcap _{i \in {\mathcal C}}\left( S\bigcap {\mathcal X}^i\right)$. For an arbitrary minimal partial covering $\mathbf {g}\in \mathcal {G}$, we must have $x\in \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right)$ since from Definition 3, $\mathbf {g}$ intersects with all feasible subsets (i.e., $\mathbf {g}\cap {\mathcal C}\ne \emptyset$). Thus, $X\subseteq X'$.

Suppose that there exists an $x'\in X'$ such that $x'\notin X$. Define a subset ${\mathcal C}':=\{i\in [N]:x'\in S\bigcap {\mathcal X}^i\}\notin \mathcal {Z}$. Let $\mathbf {g}'$ be the complement of ${\mathcal C}'$, i.e., $\mathbf {g}'=[N]\setminus {\mathcal C}'$. We claim that for all ${\mathcal C}\in \mathcal {Z}$, we have $\mathbf {g}'\bigcap {\mathcal C}\ne \emptyset$. Suppose not, then there must exist a $\widehat{{\mathcal C}}\in \mathcal {Z}$ such that $\mathbf {g}'\bigcap \widehat{{\mathcal C}}=\emptyset$. This implies that $\widehat{{\mathcal C}}\subseteq {\mathcal C}'$, and thus

$$\begin{aligned} x'\in \bigcap _{i \in {\mathcal C}'}\left( S\bigcap {\mathcal X}^i\right) \subseteq \bigcap _{i \in \widehat{{\mathcal C}}}\left( S\bigcap {\mathcal X}^i\right) \subseteq X, \end{aligned}$$

which contradicts $x'\notin X$. Hence, $\mathbf {g}'$ is a partial covering subset of $[N]$, and thus $x'\in X'\subseteq \bigcup _{i \in \mathbf {g}'}\left( S\bigcap {\mathcal X}^i\right)$; this contradicts the definition of $\mathbf {g}' = [N]\setminus {\mathcal C}'$. $\square$

Next we provide a conjunctive normal form for $S^1$. We will need the following preliminary observations.

Lemma 1

The set $\mathcal {B}_{q}^\alpha =\{i\in [N]:\beta _i^\alpha (S)\ge \beta _{q}^\alpha (S)\}$ is a partial covering subset.

Proof

From the definition of $\beta _{q}^\alpha (S)$, for any subset $\widehat{{\mathcal C}}\in \mathcal {Z}$, there must exist an $i_0\in \widehat{{\mathcal C}}$ such that $\beta _{i_0}^\alpha (S)\ge \beta _{q}^\alpha (S)$. Thus $\mathcal {B}_{q}^\alpha$ is a partial covering subset. $\square$

Lemma 2

There exist a $\mathbf {g}\in \mathcal {G}$ such that $\beta _{q}^\alpha (S)=\min _{i\in \mathbf {g}} \beta _{i}^\alpha (S)$.

Proof

By the definition of $\beta _{q}^\alpha (S)$, there exists a $\widehat{{\mathcal C}}\in \mathcal {Z}$ with $\beta _{q}^\alpha (S)=\max _{\widehat{{\mathcal C}}}\beta _{i}^\alpha (S)\ge \beta _{j}^\alpha (S)$ for all $j\in \widehat{{\mathcal C}}$. From Definition 3, for each $\widehat{\mathbf {g}}\in \mathcal {G}$, we have $\widehat{\mathbf {g}}\cap \widehat{{\mathcal C}}\ne \emptyset$. Hence, $\beta _{q}^\alpha (S)$ must be no smaller than the smallest value in set $\{\beta _{i}^\alpha (S)\}_{i\in \widehat{\mathbf {g}}}$; i.e.,

$$\begin{aligned} \beta _{q}^\alpha (S)\ge \min _{i\in \widehat{\mathbf {g}}\cap \widehat{{\mathcal C}}} \beta _{i}^\alpha (S)\ge \min _{i\in \widehat{\mathbf {g}}} \beta _{i}^\alpha (S). \end{aligned}$$

From Lemma 1, $\mathcal {B}_{q}^\alpha$ is a partial covering subset. Now let $\mathbf {g}$ be a minimal partial covering subset such that $\mathbf {g}\subseteq \mathcal {B}_{q}^\alpha$. Thus,

$$\begin{aligned} \min _{i\in \mathbf {g}} \beta _{i}^\alpha (S)\ge \min _{i\in \mathcal {B}_{q}^\alpha } \beta _{i}^\alpha (S)\ge \beta _{q}^\alpha (S). \end{aligned}$$

$\square$

Theorem 1

$$\begin{aligned} S^1=\bigcap _{\mathbf {g}\in \mathcal {G}}{{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right] , \end{aligned}$$

(12)

and for each $r\ge 2, r\in {\mathbb {Z}}_{++}$,

$$\begin{aligned} S^r=\bigcap _{\mathbf {g}\in \mathcal {G}}{{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S^{r-1}\bigcap {\mathcal X}^i\right) \right] \end{aligned}$$

where $S^0=S$.

Proof

• (i) We first prove (12).

  Let $W^{\mathbf {g}}:={{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right]$, $W:=\bigcap _{\mathbf {g}\in \mathcal {G}}W^{\mathbf {g}}$. We need to show that $S^1=W$.

  [$S^1\subseteq W$] Consider $\mathbf {g}\in \mathcal {G}$, and take any valid inequality $\alpha ^\top x\ge \beta$ for $W^{\mathbf {g}}$. Let $\widehat{C}\in \mathcal {Z}$ such that $\beta _{q}^\alpha (S)=\max _{i\in \widehat{C}}\beta _{i}^\alpha (S)$. Since $\mathbf {g}\cap \widehat{C}\ne \emptyset$ by Definition 3, hence

  $$\begin{aligned} \beta _{q}^\alpha (S)\ge \min _{i\in \mathbf {g}\cap \widehat{{\mathcal C}}}\beta _{i}^\alpha (S)\ge \min _{i\in \mathbf {g}}\beta _{i}^\alpha (S)\ge \beta . \end{aligned}$$

  Thus, $\alpha ^\top x\ge \beta$ is a valid inequality of $S^1$. This holds for any valid inequality of $W^{\mathbf {g}}$, we have that $S^1\subseteq W^{\mathbf {g}}$. Since $\mathbf {g}$ was arbitrary, it follows that $S^1\subseteq W^{\mathbf {g}}$ for all $\mathbf {g}\in \mathcal {G}$; i.e., $S^1\subseteq W$.

  [$S^1\supseteq W$] For any given $\alpha$, from Lemma 2, there exist a $\mathbf {g}\in \mathcal {G}$ such that $\beta _{q}^\alpha (S)=\min _{i\in \mathbf {g}} \beta _{i}^\alpha (S)$. Clearly, $\alpha ^\top x\ge \beta _{q}^\alpha (S)$ is a valid inequality for $W^{\mathbf {g}}$; and so it is valid for W. Thus, $S^1\supseteq W$.

• (ii) When $r\ge 2$, the statement follows directly follows from (12) by replacing S with $S^{r-1}$.$\square$

Next we show that the conjunctive normal form (12) of $S^1$ which is independent of $\alpha$ implies the polyhedrality of the quantile closures when $G_0(\cdot )$, $\{G_i(\cdot )\}_{i\in [N]}$ are rational affine mappings.

Corollary 1

For each $r\in {\mathbb {Z}}_{++}$, if $G_0(\cdot ),\{G_i(\cdot )\}_{i\in [N]}$ are rational affine functions, then $S^r$ is a polytope.

Proof

By the fundamental theorem of mixed integer program [11] and the fact that the convex hull of union of compact sets is equivalent to the convex hull of the union of convex hulls of compact sets, it follows that for any $\mathbf {g}\in \mathcal {G}$,

$$\begin{aligned} {{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right] = {{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}{{\mathrm{conv}}}\left( S\bigcap {\mathcal X}^i\right) \right] \end{aligned}$$

and is a polytope. Since $\mathcal {G}$ is a finite set, it follows from Theorem 1 that $S^1$ is a polytope.

By induction, suppose $S^{r}$ is a polytope for $r\le t$. Now let $r=t+1$, by (i), we have

$$\begin{aligned} S^r=\bigcap _{\mathbf {g}\in \mathcal {G}}{{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S^{r-1}\bigcap {\mathcal X}^i\right) \right] \end{aligned}$$

and $S^{r-1}$ is a polytope, hence $S^r$ is a polytope. $\square$

4 Convergence of quantile closures

In this section, we investigate convergence of successive rounds of quantile closure operations. Our convergence notions are with respect to the Hausdorff distance [15]. For two closed convex sets $K_1,K_2\in {\mathbb R}^n$, the Hausdorff distance $d_H(K_1,K_2)$ is defined as

$$\begin{aligned} d_H(K_1,K_2)&:=\min \left\{ \delta :K_1\subseteq K_2+B(0,\delta ),K_2\subseteq K_1+B(0,\delta )\right\} \\&:=\max \left\{ \sup _{x\in K_1}\inf _{y\in K_2}\Vert x-y\Vert _2,\sup _{x\in K_2}\inf _{y\in K_1}\Vert x-y\Vert _2\right\} , \end{aligned}$$

where $B(0,\delta )$ denotes the ball centered at origin with radius $\delta$.

We will need the following fact on the limit of a set sequence.

Lemma 3

(Proposition 2, [14]) Let $\{R^{r}\}$ be a sequence of nonempty closed convex sets such that $R^{r+1}\subseteq R^r$ for all r. Then $R^r$ converges to $\bar{R}:=\lim _{r\rightarrow \infty }R^r=\bigcap _{r=1}^\infty R^r$ with respect to the Hausdorff distance, and $\bar{R}$ is also a closed convex set.

The following lemma reveals the convergence properties of a sequence of sets produced by successive quantile closure operations.

Lemma 4

Let $\{S^{r}\}$ be a sequence of quantile closures. Then

• (i) there exists a $\bar{S} :=\lim _{r\rightarrow \infty }S^r$;

• (ii) for each $\mathbf {g}\in \mathcal {G}$, we have

  $$\begin{aligned} {{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}{{\mathrm{conv}}}\left( \bar{S}\bigcap {\mathcal X}^i\right) \right] =\bar{S}. \end{aligned}$$

  (13)

Proof

• (i) This directly follows from Lemma 3 since $\{S^r\}$ is an inclusion-wise monotone sequence of convex sets.

• (ii) Let $\bar{S}^1$ be the quantile closure operation applied to set $\bar{S}$. Since $\bar{S}=\bar{S}^1$ by the limiting operation, we have that

  $$\begin{aligned} \bar{S}=\bar{S}^1=\bigcap _{\mathbf {g}\in \mathcal {G}}{{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( \bar{S}\bigcap {\mathcal X}^i\right) \right] =\bigcap _{\mathbf {g}\in \mathcal {G}}{{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}{{\mathrm{conv}}}\left( \bar{S}\bigcap {\mathcal X}^i\right) \right] , \end{aligned}$$

  where the second equality is due to Theorem 1 and the third equality follows from the fact that the convex hull of union of compact sets is equivalent to the convex hull of union of convex hull of compact sets. Since ${{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( \bar{S}\bigcap {\mathcal X}^i\right) \right] \subseteq \bar{S}$ for all $\mathbf {g}\in \mathcal {G}$, we have that (13) holds. $\square$

Now, we are ready to prove the convergence of the quantile closure procedure to the convex hull of X.

Theorem 2

The set sequence $\{S^{r}\}$ converges to ${{\mathrm{conv}}}\left( X\right)$ with respect to the Hausdorff distance; i.e., $\bar{S}=\lim _{r\rightarrow \infty }S^r={{\mathrm{conv}}}\left( X\right)$.

Proof

From Lemma 3, we know that there exists an $\bar{S}=\lim _{r\rightarrow \infty }S^r$. Since ${{\mathrm{conv}}}(X)\subseteq S^r$ for all r, it follows that ${{\mathrm{conv}}}(X)\subseteq \bar{S}$. Thus, we only need to show that ${{\mathrm{conv}}}(X)\supseteq \bar{S}$. It suffices to show that any extreme point of the convex set $\bar{S}$ belongs to X which will complete the proof.

Consider an extreme point $\bar{x}$ of $\bar{S}$. By the identity (13) in Lemma 4 and the facts that $\bar{S}\subseteq {{\mathrm{conv}}}(S)$ and any extreme point of the convex hull of union of compact sets comes from at least one of the compact sets, it follows that there exists an $i_{\mathbf {g}}\in \mathbf {g}$ such that $\bar{x}\in \bar{S}\bigcap {\mathcal X}^{i_{\mathbf {g}}}\subseteq S\bigcap {\mathcal X}^{i_{\mathbf {g}}}$ for each $\mathbf {g}\in \mathcal {G}$.

Let $\bar{{\mathcal C}}:=\{i\in [N]:\bar{x}\in S\bigcap {\mathcal X}^i\}$. We make the following claim.

Claim

$\bar{{\mathcal C}}\in \mathcal {Z}$.

Proof

Suppose not. Let $\bar{\mathbf {g}}$ be the complement of $\bar{{\mathcal C}}$, i.e., $\bar{\mathbf {g}}=[N]\setminus \bar{{\mathcal C}}$. First of all, note that we have $\bar{\mathbf {g}}\bigcap {\mathcal C}\ne \emptyset$ for all ${\mathcal C}\in \mathcal {Z}$. Otherwise, there must exist a $\widehat{{\mathcal C}}\in \mathcal {Z}$ and $\bar{\mathbf {g}}\bigcap \widehat{{\mathcal C}}=\emptyset$, which implies that $\widehat{{\mathcal C}}\subseteq \bar{{\mathcal C}}$, a contradiction that $\bar{{\mathcal C}}\notin \mathcal {Z}$. Hence, $\bar{\mathbf {g}}$ is a partial covering subset of $[N]$. Let $\widehat{\mathbf {g}}$ be a minimal partial covering subset such that $\widehat{\mathbf {g}}\subseteq \bar{\mathbf {g}}$. Since we know that $\bar{x}\in S\bigcap X^{i_{\widehat{\mathbf {g}}}}$ for some $i_{\widehat{\mathbf {g}}}\in \widehat{\mathbf {g}}$ (i.e., $i_{\widehat{\mathbf {g}}}\in \bar{{\mathcal C}}$), we have a contradiction that $\widehat{\mathbf {g}}\cap \bar{{\mathcal C}}=\emptyset$. $\diamond$

It then follows that $\bar{x}\in \bigcap _{i\in \bar{{\mathcal C}}}S\bigcap {\mathcal X}^{i}\subseteq X$. This completes the proof. $\square$

Next we show that in the pure integer setting the convex hull of X can be obtained after a finite number of quantile closure operations.

Theorem 3

Suppose that $S \cap {\mathcal X}^i\subseteq {\mathbb {Z}}^n$ for all $i\in [N]$ (i.e., $\tau =n$), then there exists a finite $\bar{r}$ such that

$$\begin{aligned} \bar{S}=S^{\bar{r}}={{\mathrm{conv}}}\left( X\right) . \end{aligned}$$

Proof

From Theorem 2, we know that $\bar{S}={{\mathrm{conv}}}\left( X\right)$. Now we only need to show the finite convergence.

Claim 1

If ${{\mathrm{conv}}}(S^r\cap {\mathbb {Z}}^n)\ne {{\mathrm{conv}}}(X)$, then there exists a $\delta >0$ (irrespective of r) such that $d_H(S^r,{{\mathrm{conv}}}(X))\ge \delta$.

Proof

First of all, we know that all of the extreme points of ${{\mathrm{conv}}}(S\bigcap _{i \in {\mathcal C}}{\mathcal X}^i)$ is integral. By the fact that any extreme point of the convex hull of union of compact sets comes from at least one of the compact sets, ${{\mathrm{conv}}}(X)$ is integral; i.e., all of the extreme points of ${{\mathrm{conv}}}(X)$ is integral.

If ${{\mathrm{conv}}}(S^r\cap {\mathbb {Z}}^n)\ne {{\mathrm{conv}}}(X)$, then there must exist a vector $\bar{x}^0\in {\mathbb {Z}}^n{\setminus } {{\mathrm{conv}}}(X)$ such that $\bar{x}_0\in S^r$, but $\bar{x}_0 \notin {{\mathrm{conv}}}(X)$. Thus, $d_H(S^r,{{\mathrm{conv}}}(X))$ is lower bounded by the Hausdorff distance between ${\mathbb {Z}}^n{\setminus }{{\mathrm{conv}}}(X)$ and ${{\mathrm{conv}}}(X)$, which is at least

$$\begin{aligned} \sup _{y\in {{\mathrm{conv}}}(X)}\inf _{x\in {\mathbb {Z}}^n\setminus {{\mathrm{conv}}}(X)}\Vert x-y\Vert _2 \end{aligned}$$

Note that the ${\mathbf {ext}}({{\mathrm{conv}}}(X))\subseteq {{\mathrm{conv}}}(X)$, where ${\mathbf {ext}}(Y)$ denotes the set of extreme points of closed convex set Y. Thus, $d_H(S^r,{{\mathrm{conv}}}(X))$ is no smaller than

$$\begin{aligned} \sup _{{\mathbf {ext}}({{\mathrm{conv}}}(X))}\inf _{x\in {\mathbb {Z}}^n\setminus {{\mathrm{conv}}}(X)}\Vert x-y\Vert _2 \end{aligned}$$

which is clearly greater than or equal to $\delta =1$. $\diamond$

It then follows that there must exist a $\bar{r}\in {\mathbb {Z}}_{++}$ such that ${{\mathrm{conv}}}(S^{\bar{r}-1}\cap {\mathbb {Z}}^n)={{\mathrm{conv}}}(X)$; otherwise, by Claim 1, $d_H(S^r,{{\mathrm{conv}}}(X))\ge \delta$ for all r, contradicting the fact that $\lim _{r\rightarrow \infty }S^r={{\mathrm{conv}}}(X)$. Since ${{\mathrm{conv}}}(S^{\bar{r}-1}\cap {\mathbb {Z}}^n)={{\mathrm{conv}}}(X)$, then by Theorem 1, we have $S^{\bar{r}}={{\mathrm{conv}}}\left( X\right) :=\bar{S}$. $\square$

We close this section with two examples. The first shows the necessity of the compactness assumption for the convergence of the quantile closure to the convex hull, and second shows the necessity of the pure integer setting for finite convergence.

Example 1

Let $S={\mathbb R}^2,{\mathcal X}^1=\{x\in {\mathbb R}^2:0\le x_1\le 2,x_2=0\},{\mathcal X}^2=\{x\in {\mathbb R}^2:x_1=0,x_2\ge 0\},{\mathcal X}^3=\{x\in {\mathbb R}^2:x_1= 2,x_2\ge 0\},\epsilon =\frac{1}{3},p_i=\frac{1}{3},i=1,2,3$ (see Fig. 1 for an illustration). Since each feasible set contains at least two scenarios, by (3), we have ${{\mathrm{conv}}}(X)=\{x\in {\mathbb R}^2:0\le x_1\le 2,x_2=0\}$. As there are exactly two scenarios in each minimal partial covering subset, according to Theorem 1, we have $S^1=\cdots =S^r=\cdots =\bar{S}=\{x\in {\mathbb R}^2:0\le x_1\le 2,x_2\ge 0\}$. Hence, in this example, the scenario constraints do not define bounded feasible regions, and the quantile closures do not converge to the convex hull of the feasible region X; i.e., $\bar{S}\ne {{\mathrm{conv}}}(X)$. $\diamond$

Fig. 1

Illustration of Example 1

Example 2

Suppose $S=[0,2]^2,{\mathcal X}^1=\{x\in {\mathbb R}_+^2:2x_1+0.5x_2\ge 1\},{\mathcal X}^2=\{x\in {\mathbb R}_+^2:0.5x_1+2x_2\ge 1\},{\mathcal X}^3=\{x\in {\mathbb R}_+^2:x_1+x_2\ge 1\},\epsilon =\frac{1}{3},p_i=\frac{1}{3},i=1,2,3$ (see Fig. 2 for an illustration). Since each feasible set contains at least two scenarios, by (3), we have

$$\begin{aligned} {{\mathrm{conv}}}(X)={{\mathrm{conv}}}\{(1,0),(0.4,0.4),(0,1),(0,2),(2,0),(2,2)\}, \end{aligned}$$

which contains the set ${\mathcal X}^3$. By induction, we can show that

$$\begin{aligned}S^r={{\mathrm{conv}}}\{(1,0),(w_r,w_r),(0,1),(0,2),(2,0),(2,2)\}, \end{aligned}$$

where $0<w_r<0.4$ for all $r\in {\mathbb {Z}}_{++}$; i.e., $S^r\ne {{\mathrm{conv}}}(X)$ whenever $r<\infty$.

Indeed, when $r=1$, as there are exactly two scenarios in each minimal partial covering subset, according to (12), we have

$$\begin{aligned} S^1={{\mathrm{conv}}}\{(1,0),(1/3,1/3),(0,1),(0,2),(2,0),(2,2)\}, \end{aligned}$$

where $w_1=1/3\in (0,0.4)$. Suppose for $\gamma = r\ge 1$, the hypothesis holds; i.e.,

$$\begin{aligned}S^{r}={{\mathrm{conv}}}\{(1,0),(w_r,w_r),(0,1),(0,2),(2,0),(2,2)\}, \end{aligned}$$

where $0<w_r<0.4$. Now let $\gamma =r+1$, then by Theorem 1, we have

$$\begin{aligned}S^{r+1}={{\mathrm{conv}}}\{(1,0),(w_{r+1},w_{r+1}),(0,1),(0,2),(2,0),(2,2)\}, \end{aligned}$$

where $w_{r+1}=0.3+1/(30-50w_{r})\in (0,0.4)$. $\diamond$

Fig. 2

Illustration of Example 2

5 Approximate quantile closure in the polyhedral setting

In this section, we assume that $G_0(\cdot ),\{G_i(\cdot )\}_{i\in [N]}$ are rational affine mappings, in particular, $G_0(x):=d-Dx$ and $G_i(x):=b^i-A^ix$ for each $i\in [N]$ where $D\in {\mathbb {Z}}^{m_0\times n}, d\in {\mathbb {Z}}^{m_0}$ and $A^i\in {\mathbb {Z}}^{m_i\times n},b^i\in {\mathbb {Z}}^{m_i}$. We consider quantile cuts derived by restricting the choice of $\alpha$ to the rows of D and $\{A^i\}_{i\in [N]}$. Such cuts we considered in numerical studies in [12, 16].

5.1 The approximate scheme

Given a valid inequality $\alpha ^\top x\ge \beta$ of ${{\mathrm{conv}}}(X)$ with $\alpha$ chosen from the rows of D and $\{A^i\}_{i\in [N]}$, we first show that the size of $\beta$ cannot be arbitrarily large.

Proposition 4

Suppose $\alpha ^\top x\ge \beta$ is a valid inequality of ${{\mathrm{conv}}}(X)$ with $\alpha$ chosen from $\{D_{t\cdot }\}_{t\in [m_0]}\cup \{A_{t\cdot }^i\}_{t\in [m_i],i\in [N]}$. Then $\alpha ^\top x\ge \bar{\beta }$ is also a valid inequality for ${{\mathrm{conv}}}(X)$, where

$$\begin{aligned} \bar{\beta }:=\min _{\bar{q}_1,\bar{q}_2\in {\mathbb {Z}}}\left\{ \frac{\bar{q}_1}{\bar{q}_2}: \frac{\bar{q}_1}{\bar{q}_2}\ge \beta ,|\bar{q}_2|\le 2^{\phi +\psi },|\bar{q}_2|\le 2^{\phi },\gcd (|\bar{q}_1|,|\bar{q}_2|)\equiv 1\right\} , \end{aligned}$$

(14)

where $\phi ,\psi$ are two positive integer numbers.

Proof

• (i) First of all, from (3), we note that for an arbitrary extreme point $\widehat{x}$ of ${{\mathrm{conv}}}(X)$, there exists a collection ${\mathcal C}\in \mathcal {Z}$ such that $\widehat{x}$ is also an extreme point of ${{\mathrm{conv}}}(S\cap _{i\in {\mathcal C}}{\mathcal X}^i)$. Since ${{\mathrm{conv}}}(S), \{{{\mathrm{conv}}}({\mathcal X}^i)\}_{i\in [N]}$ are nonempty polytopes, and are defined by rational data, thus all the extreme points of ${{\mathrm{conv}}}(S\cap _{i\in {\mathcal C}}{\mathcal X}^i)$ are rational, and there exists a positive integer $\phi$ such that the encoding length of each extreme point of ${{\mathrm{conv}}}(X)$ is bounded by $\phi$. Here, the encoding length of a rational vector $x\in {\mathcal Q}^n$, where $x_j=\frac{q_{1j}}{q_{2j}}, q_{1j},q_{2j}\in {\mathbb {Z}}$ with $|q_{1j}|,|q_{2j}|$ relatively prime for each $j\in [n]$, is defined as

  $$\begin{aligned} n+\sum _{j\in [n]}\left[ 1+\lceil \log _2(|q_{1j}|+1)\rceil +\lceil \log _2(|q_{2j}|+1)\rceil \right] . \end{aligned}$$

• (ii) Next, suppose that the largest encoding length of each row of matrices $D,\{A^i\}_{i\in [N]}$ is at most $\psi$. Then for an $\alpha \in \left\{ D_{t\cdot }\right\} _{t\in [m_0]}\bigcup \left\{ A_{t\cdot }^i\right\} _{t\in [m_i],i\in [N]}$, optimizing $\alpha ^{\top } x$ over ${{\mathrm{conv}}}(X)$ is achieved by an extreme point $\widehat{x}$. Let $\alpha ^\top \widehat{x}:=\frac{\widehat{q}_1}{\widehat{q}_2}$ where $\widehat{q}_1,\widehat{q}_2\in {\mathbb {Z}}$ with $|\widehat{q}_1|,|\widehat{q}_2|$ relatively prime. Note that the encoding length of $|\widehat{q}_1| \le 2^{\phi +\psi }, |\widehat{q}_2| \le 2^{\phi }$ because the encoding length of each extreme point of ${{\mathrm{conv}}}(X)$ is bounded by $\phi$ and $\alpha \in {\mathbb {Z}}^n$ is of encoding length at most $\psi$. Thus, for any valid inequality $\alpha ^\top x\ge \beta$, $\frac{\widehat{q}_1}{\widehat{q}_2}$ is a feasible solution to (14). Thus, $\alpha ^\top x\ge \frac{\widehat{q}_1}{\widehat{q}_2}\ge \bar{\beta }$ is also a valid inequality to ${{\mathrm{conv}}}(X)$.$\square$

We now formally define the rounds of the approximate quantile closure below.

Definition 4

The rth round of approximate quantile closure of S is defined as

$$\begin{aligned} \widehat{S}^{r}:=\bigcap _{\begin{subarray}{c}\alpha \in \left\{ D_{t\cdot }\right\} _{t\in [m_0]}\bigcup \left\{ A_{t\cdot }^i\right\} _{t\in [m_i],i\in [N]}\end{subarray}} \left\{ x\in {\mathbb R}^n: \alpha ^\top x\ge \bar{\beta }_{q}^\alpha \left( \widehat{S}^{r-1}\right) \right\} , \end{aligned}$$

where $\widehat{S}^{0}=S$ and $\bar{\beta }$ is defined as in (14).

Clearly, $\{\widehat{S}^r\}_{r\ge 1}$ are polytopes with $m_0+\sum _{i\in [N]}m_i$ linear inequalities. Different from the infinite convergence of the quantile closure, we show that this approximate scheme converges finitely.

Theorem 4

There exists a finite $\widehat{r}$ such that $\widehat{S}^{\widehat{r}}=\lim _{r\rightarrow \infty }\widehat{S}^{r}$.

Proof

Since $\{\widehat{S}^{r}\}$ is a monotone non-increasing set sequence (i.e., $\widehat{S}^{0}\subseteq \widehat{S}^{1}\subseteq \cdots \subseteq \widehat{S}^{r}\subseteq \cdots$), it is sufficient to show that there exists a $\widehat{r}\ge 1$ such that $\widehat{S}^{\widehat{r}}=\widehat{S}^{\widehat{r}-1}$. Suppose that for any $r\ge 1$ it holds that $\widehat{S}^{r}\subsetneq \widehat{S}^{r-1}$, then from Proposition 4 there must exist $\widehat{\alpha }\in \left\{ D_{t\cdot }\right\} _{t\in [m_0]}\bigcup \left\{ A_{t\cdot }^i\right\} _{t\in [m_i],i\in [N]}$ such that $\bar{\beta }_{ q}^{\widehat{\alpha }}\left( \widehat{S}^{r}\right) -\bar{\beta }_{ q}^{\widehat{\alpha }}\left( \widehat{S}^{r-1}\right) \ge \frac{1}{(2^{\phi }-1)2^{\phi }}\ge 2^{-2\phi }$. Since $\left| \bar{\beta }_{ q}^{\widehat{\alpha }}\left( \widehat{S}^{r}\right) \right| \le 2^{\phi +\psi }$ by Proposition 4 and there are only $m_0+\sum _{i\in [N]}m_i$ choices of $\alpha$, when $r> 2^{1+3\phi +\psi }\left( m_0+\sum _{i\in [N]}m_i\right)$, we must have $\widehat{S}^{r}=\widehat{S}^{r-1}$.$\square$

5.2 Approximation error estimation for covering CCPs

Considering a covering CCP, ${\mathcal X}^i = \{x \in S: (a^i)^\top x \ge 1\}$ and $p_i = 1/N$ for all $i \in [N]$, and $S = [0,M]^n$ with $M\ge \max _{i\in [N],j\in [n]:a^i_j\ne 0}\frac{1}{a^i_j}$. From [12] we know that the first quantile closure is equivalent to

$$\begin{aligned} S^1=\bigcap _{\mathbf {g}\in \mathcal {G}} \left\{ x\in S: a_{\mathbf {g}}^\top x\ge 1\right\} , \end{aligned}$$

where $(a_{\mathbf {g}})_j=\max _{i\in \mathbf {g}}a^i_j,\forall j\in [n]$, $\mathcal {G}=\{\mathbf {g}\subseteq [N]: |\mathbf {g}|=k+1 \}$ and $k=\lfloor \epsilon N\rfloor$. Next we show a similar representation of the approximated quantile closure $\widehat{S}^1$.

Proposition 5

For a covering CCP,

$$\begin{aligned} \widehat{S}^1=\left\{ x\in S: (a^{i})^\top x\ge \bar{\beta }_{ q}^{a^{i}}\left( S\right) ,\forall i\in [N]\right\} , \end{aligned}$$

(15)

where $\bar{\beta }_{ q}^{a^{i}}\left( S\right)$ is the $(k+1)$th largest value among $\left\{ \min _{j\in [n]}\frac{a_j^i}{a_j^t}\right\} _{t\in [N]}$.

Proof

Note that when $\alpha =a^{i}$, the optimal value of scenario $t\in [N]$ is equal to $\beta _{ t}^{a^{i}}\left( S\right) =\min _{j\in [n]}\frac{a_j^i}{a_j^t}$. Thus, the quantile bound is the $(k+1)$th largest value among $\left\{ \min _{j\in [n]}\frac{a_j^i}{a_j^t}\right\} _{t\in [N]}$ by the definition. $\square$

From the definition of approximation scheme, we have $S^1\subseteq \widehat{S}^1$. The following result measures the approximation error between $S^1$ and $\widehat{S}^1$.

Proposition 6

For a covering CCP, $d_H(S^1,\widehat{S}^1)\le \left( \frac{\overline{a}}{\underline{a}}-1\right) \max _{i\in [N]}\frac{\bar{\beta }_{ q}^{a^{i}}}{\Vert a^{i}\Vert _2}$. Where $\overline{a}=\min _{i\in [N]}\max _{j\in [n]}a_j^i/\bar{\beta }_{ q}^{a^{i}}\left( S\right)$ and $\underline{a}=\min _{\mathbf {g}\in \mathcal {G}}\min _{i\in \mathbf {g}}(a_{\mathbf {g}})_i$.

Proof

(1) First of all, we would like to find a $\theta \ge 1$ such that

$$\begin{aligned} \widehat{S}^1(\theta )\subseteq S^1\subseteq \widehat{S}^1 \end{aligned}$$

where

$$\begin{aligned} \widehat{S}^1(\theta )=\left\{ x\in S: (a^{i})^\top x\ge \theta \bar{\beta }_{ q}^{a^{i}}\left( S\right) ,\forall i\in [N]\right\} . \end{aligned}$$

(16)

We make the following claim.

Claim

$\theta =\frac{\overline{a}}{\underline{a}}$ Satisfies (16), where $\overline{a}=\min _{i\in [N]}\max _{j\in [n]}a_j^i/\bar{\beta }_{ q}^{a^{i}}\left( S\right)$ and $\underline{a}=\min _{\mathbf {g}\in \mathcal {G}}\min _{i\in \mathbf {g}}(a_{\mathbf {g}})_i$.$\square$

Proof

First, we observe that $a_{\mathbf {g}}\ge \underline{a}\mathbf {e}$ for all $\mathbf {g}\in \mathcal {G}$, where $\mathbf {e}$ is an all-one vector. Thus,

$$\begin{aligned} T:=\{x\in S:\underline{a}\mathbf {e}^\top x\ge 1\}\subseteq S^1. \end{aligned}$$

We all need to show is $\widehat{S}^1(\theta )\subseteq T$. From the definition of $\overline{a}$, there exists an $i_0\in [N]$ such that $\overline{a}=\max _{j\in [n]}a_j^{i_0}/\beta _{ q}^{a^{i_0}}\left( S\right)$. Hence,

$$\begin{aligned} \widehat{S}^1(\theta )&\subseteq \left\{ x\in S: (a^{i_0})^\top x\ge \theta \beta _{ q}^{a^{i_0}}\left( S\right) \right\} \subseteq \left\{ x\in S: \overline{a}\mathbf {e}^\top x\ge \theta \right\} =T, \end{aligned}$$

where the first inclusion is due to $i_0\in [N]$, the second inclusion comes from the definition of $\overline{a}$, and the third inequality is because of $\theta =\frac{\overline{a}}{\underline{a}}$. $\diamond$

(2) To prove our main result, we first note that

$$\begin{aligned} d_H(S^1,\widehat{S}^1)\le d_H(\widehat{S}^1(\theta ),\widehat{S}^1), \end{aligned}$$

because of $\widehat{S}^1(\theta )\subseteq S^1$. Next, we show that

$$\begin{aligned} d_H(\widehat{S}^1(\theta ),\widehat{S}^1)\le \left( \theta -1\right) \max _{i\in [N]}\frac{\bar{\beta }_{ q}^{a^{i}}}{\Vert a^{i}\Vert _2}. \end{aligned}$$

This is because for any $x\in \widehat{S}^1\backslash \widehat{S}^1(\theta )$, there exists $i_1\in [N]$ such that $\beta _{ q}^{a^{i_1}}\le (a^{i_1})^\top x\le \theta \beta _{ q}^{a^{i_1}}$ (otherwise $d(x,\widehat{S}^1(\theta ))=0$), hence $d(x,\widehat{S}^1(\theta ))\le \left( \theta -1\right) \frac{\bar{\beta }_{ q}^{a^{i_1}}}{\Vert a^{i_1}\Vert _2}$, which implies that

$$\begin{aligned} d_H(\widehat{S}^1(\theta ),\widehat{S}^1)=\max _{x\in \widehat{S}^1\backslash \widehat{S}^1(\theta )}d(x,\widehat{S}^1(\theta ))\le \left( \theta -1\right) \max _{i\in [N]}\frac{\bar{\beta }_{ q}^{a^{i}}}{\Vert a^{i}\Vert _2}. \end{aligned}$$

$\square$

Suppose that for each $i\in [N]$, $a^i$ is lower and upper bounded by $\underline{M}\mathbf {e},\overline{M}\mathbf {e}$, respectively, i.e. $\overline{M}\mathbf {e}\ge a^i\ge \underline{M}\mathbf {e}$. Then we have $\beta _{ q}^{a^{i}}\left( S\right) \ge \underline{M}/\overline{M}$ and $\underline{M}\sqrt{n}\le \Vert a^i\Vert _2$ for each $i\in [N]$. It then follows that $\overline{a}\le \overline{M}$ and $\underline{a}\ge \underline{M}/\overline{M}^2$. Therefore, by Proposition 6, the distance between first quantile closure $S^1$ and its approximation $\widehat{S}^1$ is upper bounded as $d_H(S^1,\widehat{S}^1)\le \left( \frac{\overline{M}^2}{\underline{M}^2}-1\right) \frac{\overline{M}^2}{\underline{M}^2\sqrt{n}}$. Thus, in this setting, the approximation error vanishes asymptotically with problem dimension, i.e. $\lim _{n \rightarrow \infty } d_H(S^1,\widehat{S}^1) = 0$.

We close this section by showing the approximation error for Example 2. For the given data we have $\overline{a}=1,\underline{a}=0.5, \left( \frac{\overline{a}}{\underline{a}}-1\right) \max _{i\in [N]}\frac{\bar{\beta }_{ q}^{a^{i}}}{\Vert a^{i}\Vert _2}=\frac{\sqrt{2}}{4}$. The sets $\widehat{S}^1,S^1,\widehat{S}^1(\frac{\overline{a}}{\underline{a}})$ are shown in Fig. 3.

6 Generalized quantile closure

In this section, we generalize the quantile closure by grouping every $\kappa \in {\mathbb {Z}}_{++}$ scenarios together, where $\kappa$ is no larger than cardinality of the smallest feasible set in $\mathcal {Z}$ (i.e., $\kappa \le \min _{{\mathcal C}\in \mathcal {Z}}|{\mathcal C}|$). Since we now simultaneously consider multiple scenarios while computing the quantile bound, this generalization can generate stronger quantile cuts.

Note that for a given $\kappa$, there are $\left( N\right) _{\kappa }:={N\atopwithdelims ()\kappa }$ different groups, denoted as ${[N]\atopwithdelims ()\kappa }:=\{\left( \omega _{i}\right) _{\kappa }\}_{i\in [\left( N\right) _{\kappa }]}$, where $\left( \omega _{i}\right) _{\kappa }$ represents the ith group. We define the $\kappa$-quantile bound and cut as below.

Definition 5

Given $\alpha \in {\mathbb R}^n$ let $\{\beta _{i\kappa }^\alpha (S)\}_{i\in [\left( N\right) _{\kappa }]}$ be the optimal values of

$$\begin{aligned} \beta _{i\kappa }^\alpha (S)=\min \left\{ \alpha ^\top x: x\in S, x\in {\mathcal X}^j, j\in \left( \omega _{i}\right) _{\kappa }\right\} \quad \forall i\in [\left( N\right) _{\kappa }]. \end{aligned}$$

(17)

The $\kappa$-quantile $\beta _{q\kappa }^\alpha (S)$ is given by

$$\begin{aligned} \beta _{q\kappa }^\alpha (S):&=\min _{{\mathcal C}\in \mathcal {Z}} \max _{i\in [\left( N\right) _{\kappa }]: \left( \omega _{i}\right) _{\kappa }\subseteq {\mathcal C}}\beta _{i\kappa }^\alpha (S) \end{aligned}$$

(18)

and the associated “$\kappa$ -quantile cut” is

$$\begin{aligned} \alpha ^\top x\ge \beta _{q\kappa }^\alpha (S). \end{aligned}$$

(19)

Note that $\beta _{q\kappa }^\alpha (S)$ is a valid lower bound of $\min _{x\in X}\{\alpha ^{\top }x\}$, since in (17), we simply choose the smallest bound among all the possible feasible subsets. In addition, when $p_i=\frac{1}{N}$ for all $i\in [N]$, $\beta _{q\kappa }^\alpha (S)$ is the $(\left( N\right) _{\kappa }-{N-k\atopwithdelims ()\kappa }+1)$st largest value among $\{\beta _{i\kappa }^\alpha (S)\}_{i\in [\left( N\right) _{\kappa }]}$ with $k=\lfloor \epsilon N\rfloor$.

Fig. 3

Illustration of the approximation error in Example 2

Next, we generalize Definition 2 to define $\kappa$-quantile closure.

Definition 6

The rth round $\kappa$-quantile closure $S^{r}$ is defined as

$$\begin{aligned} S_{\kappa }^{r}:=\bigcap _{\begin{subarray}{c}\alpha \in {\mathbb R}^n \end{subarray}} \left\{ x\in {\mathbb R}^n: \alpha ^\top x\ge \beta _{q\kappa }^\alpha (S^{r-1})\right\} , \quad r\ge 1. \end{aligned}$$

We remark that when $\kappa =1$, we recover Definition 1. The following results establish the validity of $\kappa$-quantile cut.

Proposition 7

For any $\alpha$, $\alpha ^\top x\ge \beta _{q\kappa }^\alpha (S)$ is valid for ${{\mathrm{conv}}}(X)$.

Proof

Given $x\in X$, then there exists a feasible set $\widehat{{\mathcal C}}\in \mathcal {Z}$ such that x is contained in $S\bigcap _{i \in \widehat{{\mathcal C}}}{\mathcal X}^i$ . We claim that there must exist a $\widehat{i}\in [\left( N\right) _{\kappa }]$, such that $\left( \omega _{\widehat{i}}\right) _{\kappa }]\subseteq \widehat{{\mathcal C}}$ and $\beta _{{\widehat{i}}\kappa }^\alpha (S)\ge \beta _{q\kappa }^\alpha (S)$; otherwise,

$$\begin{aligned} \max _{i\in [\left( N\right) _{\kappa }]: \left( \omega _{i}\right) _{\kappa }\subseteq \widehat{{\mathcal C}}}\beta _{i\kappa }^\alpha (S)<\beta _{q\kappa }^\alpha (S), \end{aligned}$$

which implies existence of a strictly smaller $\kappa$-quantile bound, contradiction.

Hence, we have

$$\begin{aligned} \alpha ^\top x \ge \max _{i\in [\left( N\right) _{\kappa }]: \left( \omega _{i}\right) _{\kappa }\subseteq \widehat{{\mathcal C}}}\beta _{i\kappa }^\alpha (S)\ge \beta _{{\widehat{i}}\kappa }^\alpha (S)\ge \beta _{q\kappa }^\alpha (S). \end{aligned}$$

$\square$

Clearly, $\{S_{\kappa }^{r}\}_{r}$ is a nonincreasing set sequence with respect to r for any fixed $\kappa$. Next, we show that $\{S_{\kappa }^{r}\}_{\kappa }$ is a nonincreasing set sequence with respect to $\kappa$ for any fixed r. First we observe that for any given $\alpha$, $\{\beta _{q\kappa }^\alpha (S)\}_{\kappa }$ is a nondecreasing sequence.

Lemma 5

For any given $\alpha$, $\beta _{q(\kappa -1)}^\alpha (S)\le \beta _{q\kappa }^\alpha (S)$ with $2\le \kappa \le \min _{{\mathcal C}\in \mathcal {Z}}|{\mathcal C}|$.

Proof

Let ${\mathcal C}_{\kappa }$ be one of the feasible sets that achieve $\kappa$-quantile defined in (18). Define

$$\begin{aligned} \left( \omega _{\widehat{i}}\right) _{\kappa -1}:=\arg \max _{i\in [N_{\kappa -1}]: \left( \omega _{i}\right) _{\kappa -1}\subseteq {\mathcal C}_{\kappa }}\beta _{i(\kappa -1)}^\alpha (S). \end{aligned}$$

Since $\kappa \le \min _{{\mathcal C}\in \mathcal {Z}}|{\mathcal C}|\le |{\mathcal C}_{\kappa }|$, there exists at least one $\left( \omega _{\bar{i}}\right) _{\kappa -1}\subseteq {\mathcal C}_{\kappa }$ with cardinality $\kappa$, which contains set $\left( \omega _{\widehat{i}}\right) _{\kappa -1}$. Thus,

$$\begin{aligned}&\beta _{q\kappa }^\alpha (S)=\max _{i\in [\left( N\right) _{\kappa }]: \left( \omega _{i}\right) _{\kappa }\subseteq {\mathcal C}_{\kappa }}\beta _{i\kappa }^\alpha (S)\ge \beta _{\bar{i}\kappa }^\alpha (S)\ge \beta _{\widehat{i}(\kappa -1)}^\alpha (S) \\&=\max _{i\in [N_{\kappa -1}]: \left( \omega _{i}\right) _{\kappa -1}\subseteq {\mathcal C}_{\kappa }}\beta _{i(\kappa -1)}^\alpha (S) \ge \min _{{\mathcal C}\in \mathcal {Z}} \max _{i\in [N_{\kappa -1}]: \left( \omega _{i}\right) _{\kappa -1}\subseteq {\mathcal C}}\beta _{i(\kappa -1)}^\alpha (S) :=\beta _{q(\kappa -1)}^\alpha (S). \end{aligned}$$

where the first equality is the definition of ${\mathcal C}_{\kappa }$, the first inequality comes from $\left( \omega _{\bar{i}}\right) _{\kappa -1}\subseteq {\mathcal C}_{\kappa }$ with cardinality $\kappa$, the second inequality is due to $\left( \omega _{\widehat{i}}\right) _{\kappa -1}\subset \left( \omega _{\bar{i}}\right) _{\kappa -1}$, the second equality is the definition of $\left( \omega _{\widehat{i}}\right) _{\kappa -1}$, the third inequality is due to ${\mathcal C}_{\kappa }\in \mathcal {Z}$, while the last equality is the definition of $\kappa -1$ quantile $\beta _{q(\kappa -1)}^\alpha (S)$.$\square$

Proposition 8

For any fixed $r\in {\mathbb {Z}}_{++}$, the set sequence $\{S_{\kappa }^{r}\}_{\kappa }$ is nonincreasing.

Proof

It is sufficient to show that $S_{\kappa }^{r}\subseteq S_{\kappa -1}^{r}$ for any $2\le \kappa \le \min _{{\mathcal C}\in \mathcal {Z}}|{\mathcal C}|$. We prove it by induction on r. When $r=1$, by Lemma 5, the quantile cut $\alpha ^\top x\ge \beta _{q(\kappa -1)}^\alpha (S)$ is dominated by $\alpha ^\top x\ge \beta _{q\kappa }^\alpha (S)$ for any given $\alpha$. Thus, $S_{\kappa }^{1}\subseteq S_{\kappa -1}^{1}$. Suppose that for any $\gamma \le r$, we have $S_{\kappa }^{\gamma }\subseteq S_{\kappa -1}^{\gamma }$. Now let $\gamma =r+1$. Note that

$$\begin{aligned} \beta _{q(\kappa -1)}^\alpha (S_{\kappa }^{r}) \ge \beta _{q(\kappa -1)}^\alpha (S_{\kappa -1}^{r}) \end{aligned}$$

due to the hypothesis. Replacing S by set $S_{\kappa }^{r}$ in Lemma 5, we have

$$\begin{aligned} \beta _{q\kappa }^\alpha (S_{\kappa }^{r})\ge \beta _{q(\kappa -1)}^\alpha (S_{\kappa }^{r}) \ge \beta _{q(\kappa -1)}^\alpha (S_{\kappa -1}^{r}). \end{aligned}$$

Hence, the quantile cut $\alpha ^\top x\ge \beta _{q(\kappa -1)}^\alpha (S_{\kappa -1}^{r})$ is dominated by $\alpha ^\top x\ge \beta _{q\kappa }^\alpha (S_{\kappa }^{r})$ for any given $\alpha$. This implies that $S_{\kappa }^{r+1}\subseteq S_{\kappa -1}^{r+1}$.$\square$

The next definition is a generalization of Definition 3.

Definition 7

A set $\mathbf {g}_{\kappa }\subseteq {[N]\atopwithdelims ()\kappa }$ is a “$\kappa$-partial covering subset” if it “intersects” with all of feasible scenario subsets in $\mathcal {Z}$, i.e., for any $\widehat{{\mathcal C}}\in \mathcal {Z}$, there exists a $\omega \in \mathbf {g}_{\kappa }$ we have $\omega \subseteq \widehat{{\mathcal C}}$. Also, a set $\mathbf {g}_{\kappa }$ is a “minimal” $\kappa$-partial covering subset if there does not exist another $\kappa$-partial covering subset $\mathbf {g}_{\kappa }'\subseteq [N]$ such that $\mathbf {g}_{\kappa }'\subsetneq \mathbf {g}_{\kappa }$. We let $\mathcal {G}_{\kappa }$ denote the collection of all of the minimal partial covering subsets.

Example 3

Suppose $[N]=\{1,2,3,4\}$ with $p_i=\frac{1}{4}$ for all $i\in [N]$ and $\epsilon =0.25$ ($k:=\lfloor \epsilon N\rfloor =1$). In this case, $\mathcal {Z}=\{\{1,2,3\},\{1,2,4\},\{1,3,4\},\{2,3,4\}\}$. Let $\kappa =2$ and $\mathbf {g}_{2}=\{\{1,2\},\{1,3\},\{2,3\}\}$ be a 2-partial covering subset since for each feasible scenario subset ${\mathcal C}\in \mathcal {Z}$, there exists an element $\omega \in \mathbf {g}_{\kappa }$, which is also contained in ${\mathcal C}$. Note that $\mathbf {g}_{2}$ is also minimal since there is no other partial covering subset which has smaller size and is a subset of $\mathbf {g}_{2}$.

Similar to Theorems 1 and 2, the following two theorems demonstrate the characterization of rth $\kappa$ quantile closure using $\mathcal {G}_{\kappa }$ defined above, and the convergence of $\kappa$ quantile closure sequence. The proofs are nearly identical to those for Theorems 1 and 2 and are omitted here.

Theorem 5

For any $r\in {\mathbb {Z}}_{++}$ and $2\le \kappa \le \min _{{\mathcal C}\in \mathcal {Z}}|{\mathcal C}|$

$$\begin{aligned} S_{\kappa }^r=\bigcap _{\mathbf {g}_{\kappa }\in \mathcal {G}_{\kappa }}{{\mathrm{conv}}}\left[ \bigcup _{\omega \in \mathbf {g}}\left( S_{\kappa }^{r-1}\bigcap _{i\in \omega } {\mathcal X}^i\right) \right] , \end{aligned}$$

where $S_{\kappa }^{0}=S$.

Theorem 6

For each $2\le \kappa \le \min _{{\mathcal C}\in \mathcal {Z}}|{\mathcal C}|$, the set sequence $\{S_{\kappa }^{r}\}$ converges to ${{\mathrm{conv}}}\left( X\right)$ with respect to the Hausdorff distance; i.e., $\bar{S}_{\kappa }=\lim _{r\rightarrow \infty }S_{\kappa }^r={{\mathrm{conv}}}\left( X\right)$.

We close this section by remarking about the exactness of $\kappa$-quantile bound. Suppose each scenario occurs with equal probability, i.e. $p_i=\frac{1}{N}$ for each $i\in [N]$, and let $k=\lfloor \epsilon N\rfloor$ where $\epsilon =\frac{r}{N}$ for a constant r that is independent of N.

Let $\kappa =N-k$, and the quantile bound $\beta _{q{(N-k)}}^{c}(S)$ is the optimal value to (1), since $\left( N\right) _{\kappa }$ equals to the collection of all the feasible subsets and in this case, the quantile bound is equal to the minimum value among all the feasible subsets. Since $k=O(1)$, to compute the quantile bound $\beta _{q{(N-k)}}^{c}(S)$, we only need to solve a polynomial number (${N\atopwithdelims ()N-k}=(O(N^k))$) of optimization problems (17) with $\alpha =c$. Note that this fact does not hold for general k, for example, if $\epsilon =\frac{1}{2}$ (i.e., $k=\frac{1}{2}N$), clearly, to evaluate the quantile bound $\beta _{q{(N-k)}}^{c}(S)$, one has to solve $\Omega (2^{N}/\sqrt{N})$ number of optimization problems.

7 Separation over the first quantile closure

7.1 Complexity

We first show that separating over the first quantile closure even in the absence of integrality restrictions is NP-hard. Our proof is based on the constructions in [10] and [12].

Theorem 7

The separation over $S^1$ is, in general, NP-hard.

Proof

We consider a covering CCP where ${\mathcal X}^i = \{x \in S: (a^i)^\top x \ge 1\}$ and $p_i = 1/N$ for all $i \in [N]$, and $S = [0,M]^n$ with $M\ge \max _{i\in [N],j\in [n]:a^i_j\ne 0}\frac{1}{a^i_j}$. From [12] it can be shown that

$$\begin{aligned} S^1=\bigcap _{\mathbf {g}\in \mathcal {G}} \left\{ x\in S: a_{\mathbf {g}}^\top x\ge 1\right\} , \end{aligned}$$

(20)

where $(a_{\mathbf {g}})_j=\max _{i\in \mathbf {g}}a^i_j,\forall j\in [n]$, $\mathcal {G}=\{\mathbf {g}\subseteq [N]: |\mathbf {g}|=k+1 \}$ and $k=\lfloor \epsilon N\rfloor$ (see Definition 3).

For a given solution $\widehat{x}\in S$, to separate it from $S^1$ is equivalent to solving the following problem

$$\begin{aligned} \delta ^*=\min _{\mathbf {g}\in \mathcal {G}}\max _{i\in \mathbf {g}}\sum _{j\in [n]}a^i_j\widehat{x}_j -1, \end{aligned}$$

(21)

i.e., find a violated constraint of the form $a_{\mathbf {g}}^\top x\ge 1$ in the description (20). If $\delta ^*< 0$, then $\widehat{x}\notin S^1$; otherwise, $\widehat{x}\in S^1$. Consider the decision version of this separation problem:

(SepCCP) Given nonnegative integers $\{a^i_j\}_{i\in [N],j\in [n]}$ and a rational vector $\widehat{x}\in S$, does there exist a $\mathbf {g}\subseteq [N]$ with $|\mathbf {g}|=k+1 (k<N)$ such that $\sum _{j\in [n]}\max _{i\in \mathbf {g}}a^i_j\widehat{x}_j <1$?

Following [10] we can show that SepCCP is NP-complete via reduction from the NP-complete problem CLIQUE which asks

(CLIQUE) Given a graph with nodes V and edges E, does it contain a clique of size C?

Given an instance of CLIQUE we can construct an instance of SepCCP as $[n]=V,[N]=E,\widehat{x}_j=\frac{1}{C+1}$ for all $j\in [n]$, $k+1=\frac{1}{2}C(C-1)$ and $a_j^i=1$ if edge i contains nodes j and $a_j^i=0$ otherwise. It is easy to verify that if CLIQUE has an answer Yes, then there exists a subgraph with edges $\mathbf {g}\subseteq [N]$ and $|\mathbf {g}|=\frac{1}{2}C(C-1)$ such that

$$\begin{aligned} \sum _{j\in [n]}\max _{i\in \mathbf {g}}a^i_j\widehat{x}_j=\frac{C}{C+1}<1. \end{aligned}$$

Hence, SepCCP has an answer Yes. Conversely, if SepCCP has an answer Yes, this implies that

$$\begin{aligned} \sum _{j\in [n]}\max _{i\in \mathbf {g}}a^i_j<C+1; \end{aligned}$$

i.e., there exists a subgraph with edges $\mathbf {g}\subseteq [N]$ and $|\mathbf {g}|=\frac{1}{2}C(C-1)$, which contains at most C nodes. Clearly, thus CLIQUE has an answer Yes. $\square$

Different from $S^1$, separation over the first approximated quantile closure $\widehat{S}^1$ is easy since for a given solution $\widehat{x}$, we can verify whether $\widehat{x}\in \widehat{S}^1$ or not by simply comparing $\alpha ^{\top } \widehat{x}$ with $\bar{\beta }_{q}^\alpha \left( S\right)$ for all $\alpha \in \left\{ D_{t\cdot }\right\} _{t\in [m_0]}\cup \left\{ A_{t\cdot }^i\right\} _{t\in [m_i],i\in [N]}$. If there exists a $\widehat{\alpha }\in \left\{ D_{t\cdot }\right\} _{t\in [m_0]}\cup \left\{ A_{t\cdot }^i\right\} _{t\in [m_i],i\in [N]}$ such that $\widehat{\alpha }^{\top } \widehat{x} < \bar{\beta }_{q}^{\widehat{\alpha }}\left( S\right)$, then $\widehat{x}\notin \widehat{S}^1$ with a separating hyperplane $\widehat{\alpha }^{\top } x \ge \bar{\beta }_{q}^{\widehat{\alpha }}\left( S\right)$; otherwise, $\widehat{x}\in \widehat{S}^1$.

7.2 A heuristic separation algorithm

In this section, we introduce a heuristic separation algorithm over the first quantile closure $S^1$ inspired by Theorem 1. First of all, we relax the integrality of x variables, i.e., assume that $S\cap {\mathcal X}^i:=\{x\in {\mathbb R}^{n}:\bar{G}_i(x)\le 0\}$. Then we define a continuous relaxation set as $X^{con}:=\{x\in {\mathbb R}^n: \ \bar{G}_i(x)\le \bar{M}_i(1-z_i), \sum _{i \in [N]} p_i z_i \ge 1-\epsilon ,z \in [0,1]^N\}$ with appropriate $\{\bar{M}_i\}$, such that ${{\mathrm{conv}}}(X)\subseteq X^{con}$.

Given an optimal solution $\widehat{x}$ which optimizes $c^{\top }x$ over set $X^{con}$, it is unlikely to be feasible to X. The proposed heuristic algorithm is to find a minimal partial cover over the subset of scenarios that does not contain $\widehat{x}$. To select such a partial cover, we prioritize the scenarios by norm of the constraint violations, i.e. we sort $\{\Vert \bar{G}_i(\widehat{x})\Vert _{\infty }\}_{i\in [N]}$ in a descending order such that $\Vert \bar{G}_{\sigma (1)}(\widehat{x})\Vert _{\infty }\ge \cdots \ge \Vert \bar{G}_{\sigma (N)}(\widehat{x})\Vert _{\infty }$ where $\sigma$ is a permutation of $[N]$, then select the scenarios according to this order until total probability mass is strictly greater than $\epsilon$. Let $\nu :=\min \{j\in [N]:\sum _{i=1}^jp_{\sigma (i)}>\epsilon \}$ and $\mathbf {g}:=\{\sigma (i)\}_{i\in [\nu ]}$. By Theorem 1, if $\widehat{x}$ can be separated from ${{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right]$, then it can be also separated from $S^1$. To separate $\widehat{x}$, we consider the following optimization problem that minimizes 2-norm distance between set ${{\mathrm{conv}}}\left[ \bigcup _{i \in \mathbf {g}}\left( S\bigcap {\mathcal X}^i\right) \right]$ and point $\widehat{x}$:

$$\begin{aligned} \delta ^*=\min _{x,\lambda } \&\Vert \widehat{x}-x\Vert _2^2 \end{aligned}$$

(22a)

$$\begin{aligned} \text {s.t. }&\lambda _{i}\bar{G}_i(x^i/\lambda _i)\le 0, \ i \in \mathbf {g}, \end{aligned}$$

(22b)

$$\begin{aligned}&\sum _{i\in \mathbf {g}}x^i=x,\end{aligned}$$

(22c)

$$\begin{aligned}&\sum _{i\in \mathbf {g}}\lambda _i=1,\end{aligned}$$

(22d)

$$\begin{aligned}&\lambda _i\ge 0, \quad \forall i\in \mathbf {g}. \end{aligned}$$

(22e)

where $\lambda _{i}\bar{G}_i(x^i/\lambda _i)$ is the perspective function associated with $\bar{G}$ and is jointly convex in $(\lambda _{i},x^i)$. The system (22b)–(22e) provides an equivalent reformulation of ${{\mathrm{conv}}}[\bigcup _{i \in \mathbf {g}}(S\bigcap {\mathcal X}^i)]$ (see [4] for details). Note that for each $i\in [N]$, if $\bar{G}_i(x)$ is second order cone representable, then (22b) is second order cone. The separation problem (22) is a convex optimization problem, which is relatively easy to solve. Given an optimal solution $(x^*,\lambda ^*)$ of (22) with optimal objective value $\delta ^*$, we check if $\delta ^*>0$, then $\widehat{x}\notin S^1$ with a separating hyperplane $(\widehat{x}-x^*)^\top (x-x^*)\le 0$, which is valid for all $x\in S^1$. Thus, we can add this valid inequality to $X^{con}$ and repeat the above steps until we cannot separate any more. The detailed procedure is described in Algorithm 1. The output (i.e., set E) can be directly added to (4).

We remark that Algorithm 1 can be applied to the generalized quantile closure. However, it might be expensive to enumerate all the $\kappa$-groups in ${[N]\atopwithdelims ()\kappa }$ when $\kappa \ge 2$. Suppose that $\kappa$ is a divisor of N, then we can consider the partition $\bar{G}_{\kappa }$ of set [N] by evenly dividing set [N] into $\frac{N}{\kappa }$ groups, i.e., $\bar{G}_{\kappa }=\{\mathbf {g}_{j}\}_{j\in [N/\kappa ]}$ with $\mathbf {g}_{j}=\{(j-1)\kappa +1, \ldots , j\kappa \}$. Next, we let $\widehat{p}_{j}=\min _{i\in \mathbf {g}_{j}}p_i$ for each $j\in [N/\kappa ]$. Then by Proposition 1 in [2], we have that the following CCP yields a relaxation of (4)

$$\begin{aligned} \min _{x\in S,\widehat{z} \in \{0,1\}^{N/\kappa }} \left\{ c^{\top }x : \ x \in S, \ G_i(x)\le M_i(1-\widehat{z}_j),\forall i\in \mathbf {g}_j ,\forall j \in [N/\kappa ], \ \sum _{j\in [N/\kappa ]} \widehat{p}_{j}\widehat{z}_j \ge 1-\widehat{\epsilon }\right\} ,\nonumber \\ \end{aligned}$$

(23)

where $\widehat{\epsilon }:=1+\epsilon -\sum _{j\in [N/\kappa ]} \widehat{p}_{j}$. Now we can apply Algorithm 1 to the relaxed CCP (23).

8 Numerical illustration

In this section, we present a numerical study to illustrate Algorithm 1 and the strength of quantile cuts. We consider the following norm optimization problem, which has also been studied in [7, 17],

$$\begin{aligned} \min _{x,z} \left\{ c^{\top }x : x\in [0,100]^n, \ \sum _{i\in [N]}p_i\mathbb {I}\left[ \sum _{j=1}^n\xi _j^ix_j^2\le 100\right] \ge 1-\epsilon \right\} , \end{aligned}$$

(24)

where the support $\{\xi ^i\}^n_{i=1}$ of ${\varvec{\xi }}$ are non-negative. We consider the cases when $n\in \{10,20,30\},N\in \{60,80,100\}$, $\epsilon \in \{0.05,0.10,0.15\}$, and each scenario occurs with equal probability, i.e. $p_i=\frac{1}{N}$. The cost vector c and unknown data $\{\xi ^i\}_{i\in [N]}$ are randomly generated, where each component of the cost vector c is integral and randomly distributed between $-10$ and $-1$ with equal probability, and $\xi _j^i$ is also integral and uniformly distributed between 1 and 99. Under this setting, the MINLP reformulation (4) is

$$\begin{aligned} \min _{x,z} \left\{ c^{\top }x : x\in [0,100]^n, \ \sum _{j=1}^n\xi _j^ix_j^2\le 100+ (M_i-100)(1-z_i),\forall i\in [N], \ z \in Z \right\} ,\nonumber \\ \end{aligned}$$

(25)

where $M_i=100\sum _{j=1}^n\xi _j^i$ suffices for each $i\in [N]$. In this case, the separation problem (22) is equivalent to a second order cone program

$$\begin{aligned} \delta ^*=\min _{x,\lambda } \&\Vert \widehat{x}-x\Vert _2^2\end{aligned}$$

(26a)

$$\begin{aligned} \text {s.t. }&\sum _{j=1}^n\xi _j^i(x_j^i)^2\le 100\lambda _{i}^2, \ i \in \mathbf {g}, \end{aligned}$$

(26b)

$$\begin{aligned}&\sum _{i\in \mathbf {g}}x^i=x,\end{aligned}$$

(26c)

$$\begin{aligned}&\sum _{i\in \mathbf {g}}\lambda _i=1,\end{aligned}$$

(26d)

$$\begin{aligned}&\lambda _i\ge 0,\quad \forall i\in \mathbf {g}. \end{aligned}$$

(26e)

We compare three solution approaches. The first one is to run Algorithm 1 and add all separated quantile cuts to (25), the second is to run Algorithm 1 to separate generalized quantile cuts for $\kappa =2$ for the relaxation (23), and finally to use the commercial solver CPLEX to solve the formulation without any quantile cuts. The overall time limit is set to be 4 h. The results are listed in Table 1, where the optimality gap is computed as

$$\begin{aligned} |\text {best upper bound}|/\text {best lower bound}|-1. \end{aligned}$$

We use $t_{\mathrm {sep}}, t_{\mathrm {C}}, t_{\mathrm {total}}$ to denote the running time of Algorithm 1, the running time of solver CPLEX and overall running time, respectively, and use $\mathrm {g}_{r}$ and $\mathrm {g}_{e}$ (%) to denote the optimality gap at root node and the best optimality gap when the solution procedure is completed. All instances were executed on a laptop with a 2.67 GHz processor and 4GB RAM, while CPLEX 12.5.1 was used with its default setting.

Table 1 Performance of CPLEX with and without quantile cuts

In Table 1, we observe that the quantile cuts separated using Algorithm 1 can reduce the root gap from more than $450\%$ to within $45\%$, while the 2-quantile cuts further reduce the root gap to within $25\%$. CPLEX with quantile cuts can solve 22 out of 27 instances within time limit, and with 2-quantile cuts can solve 23 out of 27, while CPLEX without the cuts can only solve 17 out of 27. For the unsolved instances, the average remaining gaps ($8.8, 6.8\%$) for the first two methods are also much smaller than for the third ($14.2\%$). Comparing the first and second methods with the third one, we see that the quantile cuts help reduce nearly more than half of the solution time for those instances that can be solved within time limit. Comparing the total running time for first two methods with that of the third one, there are still 22 out of 27 and 14 out of 27 instances which take a shorter time or smaller ending gap for the first method. These results demonstrate the effectiveness of quantile cuts and 2-quantile cuts separated using Algorithm 1 for solving a convex chance constrained problem. We also note that the separation time of first method with quantile cuts is usually shorter than the second one with 2-quantile cuts. However, the second method has a much smaller root gap, therefore, it can solve more instances or have smaller ending gaps. Hence, we recommend to use $\kappa$-quantile cuts over regular quantile cuts to solve the large-scale instances.

9 Conclusion

In this paper, we studied a family of cuts known as quantile cuts for chance constrained mixed integer convex program with finite support. We showed the following results (1) the closure of all quantile cuts can be described in a finite conjunctive normal form; (2) successive application of quantile closure operation achieves the convex hull of the chance constrained problem in the limit; and (3) in the pure integer setting this convergence is finite, and (4) separation of quantile cuts is in general NP-hard. For chance constrained mixed integer linear program, we also proposed an approximate quantile closure by restricting attention to original problem constraints. We generalized the quantile closure by grouping a number of scenarios together. We proposed a heuristic separation algorithm to generate quantile cuts from the first closure, and presented numerical studies to demonstrate that these cuts could strengthen the root gaps significantly and help with overall performance. Interesting future research directions include analyzing the strength of the quantile closure and establishing the quantile rank, i.e. the minimum number of closure operations required to achieve the convex hull, for some structured chance constrained problems. Finally, note that some of the results in this paper can also be applied to generalized disjunctive programming [5, 13] by choosing each ${\mathcal X}^i$ as a disjunctive set and $Z$ as logic constraints.