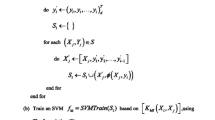Markov-Miml: A Markov chain-based multi-instance multi-label learning algorithm

Abstract

The main aim of this paper is to propose an efficient and novel Markov chain-based multi-instance multi-label (Markov-Miml) learning algorithm to evaluate the importance of a set of labels associated with objects of multiple instances. The algorithm computes ranking of labels to indicate the importance of a set of labels to an object. Our approach is to exploit the relationships between instances and labels of objects. The rank of a class label to an object depends on (i) the affinity metric between the bag of instances of this object and the bag of instances of the other objects, and (ii) the rank of a class label of similar objects. An object, which contains a bag of instances that are highly similar to bags of instances of the other objects with a high rank of a particular class label, receives a high rank of this class label. Experimental results on benchmark data have shown that the proposed algorithm is computationally efficient and effective in label ranking for MIML data. In the comparison, we find that the classification performance of the Markov-Miml algorithm is competitive with those of the three popular MIML algorithms based on boosting, support vector machine, and regularization, but the computational time required by the proposed algorithm is less than those by the other three algorithms.

1 Introduction

The evaluation of the importance of a set of labels associated with an object is an important research problem in machine learning that can assist in many data mining tasks. An object with multiple labels means that it may belong to several different classes; for instance, a patient (as an object) can suffer from several different diseases (as multiple classes) at the same time; a text document (as an object) for a medical disease can be given by several Medical Subject Index categories (as multiple classes). In these two examples, an object is only described by a single instance. In the literature, there are many approaches to evaluating the importance of multiple labels associated with a single-instance object, see for instance [7, 24, 26, 34].

On the other hand, we can consider an object described by multiple instances; for instance, in bioinformatics, a DNA sequence (as an object) can be encoded by a number of segments (as multiple instances) where the gene expression of such sequence corresponds to several different functional mechanisms in biology (as multiple classes). In image classification, an image (as an object) usually containing several different patches (as multiple instances) can correspond to several semantic meanings simultaneously (as multiple classes). In text categorization, a document (as an object) consisting of several sections (as multiple instances) can be assigned to several different topics (as multiple classes). In this paper, we are interested to tackle multi-instance multi-label (MIML) learning problems.

While most of the machine learning algorithms are designed to handle multi-label data, they are not targeted for MIML data. A simple technique has been considered and used to decompose a MIML problem into traditional multi-label learning problems. The idea is to use constructive clustering technique to generate a dictionary space to describe a bag of instances as a single instance in histograms over the dictionary space. However, this degeneration process may lose some useful information encoded in instances and their relations to class labels of objects, and therefore, the learning performance may be degraded.

In this paper, we propose a novel Markov chain-based multi-instance multi-label (Markov-Miml) learning algorithm to evaluate the importance of a set of labels associated with objectss of multiple instances. The algorithm computes their ranks to indicate the importance of a set of labels to an object. Our approach is to exploit the relationships between instances and labels of objects. The rank of a class label to an object depends on (i) the affinity metric between the bag of instances of this object and the bag of instances of the other objects, and (ii) the rank of a class label of similar objects. An object, which contains a bag of instances that are highly similar to bags of instances of the other objects with high rank of a particular class label, receives a high rank of this class label. In the algorithm, we construct a Markov transition probability matrix to represent affinity among instances and then employ instance-to-object-relation matrix to transfer from the affinity information at the instances level to the objects level. The proposed approach is basically a kind of nearest neighbor approach which makes use of neighbors’ information to learn the correct labels. Experimental results on benchmark data have shown that the proposed algorithm is computationally efficient and effective in label ranking for MIML data. In the comparison, we find that the classification performance of the Markov-Miml algorithm is competitive with those of the three popular MIML algorithms based on boosting, support vector machine, and regularization, but the computational time required by the proposed algorithm is less than those by the other three algorithms.

The rest of the paper is organized as follows. In Sect. 2, we review existing MIML learning algorithms. In Sect. 3, we present the proposed algorithm. In Sect. 4, we present and discuss the experimental results on two benchmark data sets. Finally, we give some concluding remarks in Sect. 5.

2 Related works

The MIML learning [39] is a generalization of multi-label (ML) learning and multi-instance (MI) learning.

In multi-label learning (ML) [20, 24], the classes are not mutually exclusive so that an object can be relevant to more than one class. A number of multi-label algorithms have been proposed [29]. The most naive approach for multi-label learning is to divide the problem into multiple binary classification problems [13]. A different approach toward multi-label learning is based on label ranking. This approach is to learn a model that outputs an ordering of the class labels according to their relevance to a given object. Label ranking poses a very interesting and useful approach toward multi-label learning and applied successfully to applications in gene, text, and image data, see for instance [3, 14, 27, 34]. In these classification ranking analysis methods, each object is assumed to be described by one single instance.

Multi-instance learning (MI) is formulated and studied by Dietterich et al. [6]. This framework assumes the instances are contained in a bag and the instance labels are hidden. But the bag is labeled as a positive item if any single instance in it is positive, otherwise it is labeled as a negative item. The task is to learn a model that generalizes well to predict a label for an unseen bag. Following the Dietterich et al. work, several new algorithms have emerged, see for instance [18, 21, 38]. Many approaches extend support vector machines methods which have been highly successful in traditional supervised learning problems, for MI data [2, 4, 10, 30]. In [2, 4], the modified support vector machines are studied. In [10, 15], multi-instance kernels are designed and then standard support vector machines can be employed. In [30], a random walk algorithm is used to infer positive instances and then the standard support vector machine is used to solve the resulting problem. More works on multi-instance learning can be found in [5, 8, 36].

The MIML problem [39] has been recently proposed and studied, where each object is represented by multiple instances and also associated with multiple labels. It is obvious that a ML learning problem and a MI learning problem can be regarded as a degenerated problem of MIML learning. Therefore, it is natural to solve the MIML problem by decomposing it into traditional supervised ML or MI learning problems.

By using the structure of multi-label, an MIML algorithm based on support vector machine can be developed (Miml Svm) [37]. The idea is to transform the MIML task into multi-label learning problems. More precisely, each object with a bag of instances is mapped into a new object with only one instance by using constructive clustering, see Fig. 1. Usually, it can be done by performing the $k$-means clustering algorithm at the level of instances. Then, the resulting multiple labels problem can be solved by the SVM algorithm such as Ml Svm [3]. Ml Svm algorithm deals with multi-label problem by further decomposing the problem into multiple binary problems.

Fig. 1

Two possible approaches for MIML problem

On the other hand, by using the structure of multiple instances, an MIML algorithm based on boosting can be developed (Miml Boost) [37]. The idea is to convert each MIML object into multiple single-label objects with multiple instances and then to solve the derived multiple instances learning problem by boosting algorithms such as Mi Boosting [31], see Fig. 1. Mi Boosting deals with multi-instance problem by further decomposing the problem into an single-instance problem under the assumption that each instance in the object contributes equally and independently to the label of the object.

Miml Boost and Miml Svm transforming MIML problem into multi-instance single-label (MISL) problems and single-instance multi-label (SIML) problems. We note that by using the same degeneration process as that used in Miml Boost and Miml Svm, there are other alternatives to solve the MIML task. For example, by using Ml-knn [34] (a lazy learning approach to multi-label learning) to replace the Ml Svm used in Miml Svm, we obtain Miml-knn. Other MIML algorithms can be developed by taking alternative options. But we remark that solving MIML problems by using the above two degeneration processes (using multi-instance learning or multi-label learning as the bridge) may lose some useful information encoded in instances and their relations to class labels of objects. Therefore, the learning performance may be degraded. Furthermore, it is very time-consuming to solve a number of derived traditional learning problems and not favorable in large-scale data sets with a large number of instances and classes. In the recent study given in [33], an image scene MIML data set comprised of 18,000 instances in 2,000 objects is used, it takes more than 100 h for training to learn the problem by the Miml Boost algorithm using the default parameter setting.

Following the work of these two approaches, substantial research has been carried out in image analysis, text categorization, and bioinformatics [12, 16]. Recently, Zhang and Zhou [32] design a M$^3$ Miml algorithm based on regularization to explicitly exploit the relationships between instances and labels. The idea is to formulate the learning task as a quadratic programming problem and implemented in its dual form. Experimental results show that this algorithm achieves superior performance than Miml Svm and Miml Boost algorithms for MIML learning. Furthermore, the M$^3$ Miml algorithm runs greatly faster than the Miml Boost. However, the computational cost of this learning algorithm can be still high (see the computational results in Sect. 4).

The main aim of this paper is to propose an effective and efficient Markov-Miml learning algorithm to avoid a very high computational cost of learning for MIML data and maintain a good classification performance. The idea of the proposed algorithm is basically a kind of nearest neighbor approach which makes use of neighbors’ information to learn the correct labels. Our method is to set up the affinities among objects on MIML data and compute objects’ label ranking scores based on their neighbors’ affinities and labels, in a Markov chain setting. To the best of our knowledge, our work is the first attempt to formulate the MIML though a Markov chain setting.

3 The Markov-Miml algorithm

3.1 Notations

In this subsection, we first describe notations. Let $\mathcal X$ be a set of objects and $\mathcal Y$ be a set of labels or classes. We denote the size of $\mathcal Y$ by $c = |\mathcal Y |,$ and the size of $\mathcal X$ by $m = m^{\prime } + m^{\prime \prime } = |\mathcal X |,$ where $m^{\prime }$ and $m^{\prime \prime }$ are the sizes of training data and testing data, respectively.

In the single-instance single-label learning setting, each object (i.e., only one instance) $X \in \mathcal X$ is assigned a single class $Y \in \mathcal Y .$ The task is to learn a classifier $\phi : \mathcal X \rightarrow \mathcal Y$ which minimizes the probability that $\hat{Y} \ne \phi (\hat{X})$ on a newly observed object $\hat{X}$ with its label $\hat{Y}.$ In the MIML scenario, the training data set is $\{(X_1,Y_1),(X_2,Y_2),\ldots ,(X_m,Y_m)\},$ where the $i$th object $X_i = \{ x_1^{(i)} ,\ldots ,x_{n_i}^{(i)} \}$ contains a bag of $n_i$ instances, and $Y_i = \{ y_1^{(i)} ,\ldots ,y_{l_i}^{(i)} \} \subset \{1,2,\ldots ,c\}$ is a set of labels assigned to $X_i.$ The testing data set is ${X_{m^{\prime }+1},\ldots ,X_{m^{\prime }+m^{\prime \prime }}}$ without labels information. Here, $n_i$ refers to the number of instances in $X_i,$ $l_i$ refers to the number of labels in $Y_i.$ We note that the single-instance single label is a special case in which $n_i=1$ and $l_i=1$ for all the objects.

In this paper, we are primarily interested in classifiers which generate a ranking of possible labels for a given object such that its correct labels receive higher ranking than the other irrelevant labels. Formally, the task of learning is to construct a function of the form $f:2^\mathcal{X } \rightarrow 2^\mathcal{Y }.$ For a newly observed object $\hat{X}$ with its labels $\hat{Y},$ the labels of $\hat{X}$ in $\mathcal Y$ should be ordered according to $f(\hat{X},\cdot ).$ If $f( \hat{X}, u )> f( \hat{X}, v ),$ the label $u$ is considered to be ranked higher than the label $v.$ The classifier is evaluated in terms of its ability to predict a good approximation of ranks for labels $\hat{Y}$ associated with a newly observed object $\hat{X},$ that is, the rank scores in $\hat{Y}$ should be higher than those not in $\hat{Y}.$

3.2 Relationships between instances and objects

The main idea of the proposed algorithm is to set up the affinities among objects on MIML data and initialize label information from labeled objects. All objects then spread their label ranking scores to their neighbors based on their affinities in a Markov chain setting, for instance see Fig. 2. The spread process is repeated until a global steady state is reached. As there are multiple instances among objects in MIML data, the main challenge is how to evaluate the affinity between the two objects which may have different set of instances. Our approach is to exploit the relationships among instances and labels of objects. The rank of a class label to an object depends on (i) the affinity metric between the bag of instances of this object and the bag of instances of the other objects, and (ii) the rank of a class label of similar objects. An object, which contains a bag of instances that are highly similar to bags of instances of the other objects with high rank of a particular label, receives a high rank of this label.

Fig. 2

An example of Markov chain setting for four objects (circles), eight instances (squares), and four classes (hexagons)

In the algorithm, we first construct an affinity matrix to represent affinity among instances and then employ instance-to-object-relation matrix to transfer the affinity information among instances to the label information among objects. We assume that the instances are ordered as follows:

$$\begin{aligned} \underbrace{x_1^{(1)} ,\ldots ,x^{(1)}_{n_1}}_\mathrm{1st \ object}, \underbrace{x_1^{(2)} ,\ldots ,x^{(2)}_{n_2}}_\mathrm{2nd \ object}, \cdots , \underbrace{x_1^{(m)} ,\ldots ,x^{(m)}_{n_m}}_\mathrm{mth \ object} \end{aligned}$$

For simplicity, we set $n$ to be the total number of instances in the MIML data, that is, $n = \sum _{i=1}^{m} n_i.$ Let $a_{i,j,s,t}$ be the affinity between the $s$th instance of the $i$th object and the $t$th instance of the $j$th object. We note that $a_{i,j,s,t}$ is always nonnegative as its value represents the affinity; for instance, the affinity in the intrinsic manifold structure of data (Gaussian kernel function used to yield the nonlinear version of affinity) can be used [1, 17]:

$$\begin{aligned} a_{i,j,s,t} = \exp \left[ \frac{- ||x^{(i)}_{s} ,x^{(j)}_t ||^2}{2 \sigma ^2} \right], \end{aligned}$$

where $||x^{(i)}_{s} ,x^{(j)}_t ||$ is the Euclidean distance between the $s$th instance of the $i$th object and the $t$th instance of the $j$th object, and $\sigma$ is a positive number to control the linkage in the manifold, we set $\sigma = 0.2$ as default.

Typically, correctness and appropriateness are two crucial characteristics of a good kernel. A good kernel $k$ can match the data well, that is, $k(u_i ,u_j ) = 1 \Leftrightarrow u_i = u_j$ and $k(u_i ,u_j ) = 0 \Leftrightarrow u_i \ne u_j,$ where $u_i$ and $u_j$ are the data points. An appropriate kernel generalizes well, that is, a learning algorithm achieves a high accuracy when it learns the data from the kernel space. Different kernels create different geometrical structures of the data in the kernel space. In this paper, we employ the Gaussian kernel as the affinity function similar to that used in other MIML learning algorithms [35, 37, 39]. The Gaussian kernel is a good kernel that performs ideally in terms of above-mentioned properties. Given the parameter $\sigma ,$ the Gaussian kernel is defined in a form of $k(u_i,u_j) = e^{{{ - \Vert {u_i - u_j} \Vert } \mathord {/ {} } {\sigma ^2 }}}.$ The output value of the Gaussian kernel matrix lies in between o and 1, and the main diagonal entries of kernel matrix are equal to 0. As a result, the following relationship $(k(u_i,u_j)|u_i=u_j)>(k(u_i,u_j)|u_i\ne u_j),$ does always hold. On the other hand, the parameter $\sigma$ can be used to tune how much generalization is done. A small value ($\sigma \rightarrow 0$) will force the kernel matrix entries toward 0, and a large $\sigma$ ($\sigma \rightarrow \infty$) will force the entries toward 1. Shawe-Taylor and Cristianini [25] pointed out that it is feasible to select an appropriate $\sigma ,$ which can lead to good generalization performance in learning.

Now, we can construct a $n$-by-$n$ block matrix $\mathbf{A} = [ \mathbf{A}_{i,j} ]$ where the $(i,j)$th block is an $n_i$-by-$n_j$ matrix $\mathbf{A}_{i,j} = [ a_{i,j,s,t} ]_{s=1,\ldots ,n_i,t=1,\ldots ,n_j}$ referring to the affinities among the instances in the $i$th object and the $j$th object based on the Gaussian kernel.

Next, we construct a block diagonal matrix $\mathbf{B} = [ \mathbf{B}_{i,j} ]$ where the $(i,j)$th block is a zero matrix except $i=j.$ For the $(i,i)$th block, $\mathbf{B}_{i,i}$ is a $1$-by-$n_i$ matrix where all its entries are equal to 1. This block indicates the relationship between the $i$th object and its association instances. The size of $\mathbf{B}$ is $m$-by-$n,$ and it refers to be an object-to-instance-relation matrix that can be used to transfer from the affinity information at the instances level to the objects level. The resulting $m$-by-$m$ matrix $\mathbf{B} \mathbf{A} \mathbf{B}^\mathrm{T}$ represents the affinities among objects.

3.3 Markov chain setting with restart

Motivated by the idea of topic-sensitive PageRank [11] and random walk with restart [28], our approach is to imagine a random walker starting from training objects with the known labels. The walker iteratively visits to its neighborhood with the probability that is proportional to the affinities among objects. According to $\mathbf{B} \mathbf{A} \mathbf{B}^\mathrm{T},$ we construct an $m$-by-$m$ transition probability matrix $\mathbf{Q} = [q_{i,j}]$ by normalizing the entries of $\mathbf{B} \mathbf{A} \mathbf{B}^\mathrm{T}$ with respect to each column, that is, each column sum of $\mathbf{Q}$ is equal to one. The entries of $\mathbf{Q}$ give the estimates of the conditional probabilities:

$$\begin{aligned} q_{i,j} = \mathrm{Prob} [ Z_{t} = i | Z_{t-1} = j ], \quad 1 \le i,j \le m, \end{aligned}$$

that is required in the Markov chain setting. Here, $Z_t$ is a random variable referring to visit at any particular object at the time $t.$

In the Markov chain setting with restart, it has probability $\alpha$ to return to training objects at each step. It can be interpreted that during each iteration, each object receives the label information from its neighbors via the Markov chain and also retains its initial label information. The parameter $\alpha$ specifies the relative amount of the information from its neighbors and its initial label information. In this approach, the walker has the steady-state probabilities that will finally stay at different objects. These steady-state probabilities give ranking of labels to indicate the importance of a set of labels to a test object [28].

More formally, we make use of the following equation:

$$\begin{aligned} (1- \alpha ) \mathbf{Q} \mathbf{p}_l + \alpha \mathbf{d}_l = \mathbf{p}_l, \quad 1 \le l \le c, \end{aligned}$$

(1)

where $\mathbf{p}_l$ is the probability distribution vector of size $m$ corresponding to the $l$th class label, $\mathbf{d}_l$ is the assigned probability distribution vector of the $l$th class label that are constructed from the training data, and $0 < \alpha <1$ is a parameter for controlling the importance of the assigned probability distributions in the training data to the resulting label ranking scores of objects. Both the summations of the entries of $\mathbf{p}_l$ and $\mathbf{d}_l$ are equal to 1. Given the training data, one simple way to construct $\mathbf{d}_l$ is by using an uniform distribution on the objects with the label class $l.$ More precisely,

$$\begin{aligned}{}[\mathbf{d}_l ]_i = \left\{ \begin{array}{cl} 1/ e_l,&\quad \mathrm{if} \ l \in Y_i \\ 0,&\quad \mathrm{otherwise}. \\ \end{array} \right. \end{aligned}$$

(2)

where $e_l$ is the number of objects with the label class $l$ in the training data. The steady probability distribution vector $\mathbf{p}_l$ can be solved by the iteration method as follows.

The overall algorithm is implemented in the framework shown in Fig. 3 and summarized in Algorithm 1, and the Markov-Miml computations require several iterations. In the algorithm,

$$\begin{aligned} \mathbf{P} = [ \mathbf{p}_1, \mathbf{p}_2, \ldots , \mathbf{p}_c ] \end{aligned}$$

and

$$\begin{aligned} \mathbf{D} = [ \mathbf{d}_1, \mathbf{d}_2, \ldots , \mathbf{d}_c ]. \end{aligned}$$

We set an initial matrix $\mathbf{P}_0$ (the same size of $\mathbf{P}$) where each column is a probability distribution vector. The main computational cost depends on the cost of performing operations in step 2. Assume that there are $O(N)$ nonzero entries in $\mathbf {Q},$ the cost of these calculations is of $O(N)$ arithmetic operations. Theoretically, we have the following theorem to guarantee the solution of (1) and the convergence of Algorithm 1. The proof can be found in “Appendix 6.”

Fig. 3

The flowchart of the overall implementation

Theorem 1

Suppose $\mathbf{Q}$ is a transition probability matrix and $\mathbf{D}$ is given in (2), then there exists a unique nonnegative matrix $\mathbf{P}$ such that

$$\begin{aligned} (1- \alpha ) \mathbf{Q} \mathbf{P} + \alpha \mathbf{D} = \mathbf{P}. \end{aligned}$$

Moreover, Algorithm 1 converges for any initial matrix $\mathbf{P}_0$ where each column is a probability distribution vector.

 

After solving $\mathbf{P}$ by using Algorithm 1, we generate a ranking of the possible labels for a test object $x^{(i)}_k$ by ordering the values of each row of $\mathbf{P}$: $p_{i,1}, p_{i,2}, \ldots , p_{i,c}$ where $i$ refers to the $i$th object ($i=m^{\prime }+1,\ldots ,m^{\prime }+m^{\prime \prime }$) and $c$ refers to the number of classes, such that its correct labels receive higher ranking than the other irrelevant labels. In Sect. 4, the classifier will be evaluated in terms of its ability to predict a good approximation of ranks for labels associated with a test instance.

Remark 1

We remark that when the affinity matrix $\mathbf{B} \mathbf{A} \mathbf{B}^\mathrm{T}$ is employed instead of $\mathbf{Q}$ in (1), there is no guarantee that solution $\mathbf{P}$ exists. Moreover, even if solution $\mathbf{P}$ in (1) exists, the magnitude of entries of each column of $\mathbf{P}$ may not be normalized. Thus, the values of each row of $\mathbf{P}$ may not be comparable. However, in the Markov chain setting, we have the unique solution in (1). Also, each column of $\mathbf{Q}$ is normalized, and therefore, each column sum of $\mathbf{P}$ is equal to one. It is straightforward to compare the values of each row of $\mathbf{P}$ to compute ranking of labels for a test object.

Remark 2

The proposed approach is basically a kind of nearest neighbor approach which makes use of neighbors’ information to learn the correct labels. However, the computational procedure is different from multi-label $k$-nearest neighbor (Ml-knn) method [34]. In Ml-knn method, for each unseen object, its $k$ nearest neighbors in the training set are firstly identified. Then, based on the number of neighboring object belonging to each possible class, maximum a posteriori (MAP) principle is utilized to determine the label set for the unseen object.

In the proposed method, the labeled information iteratively spreads through the neighbor according to the transition probability in the Markov chain. Additionally, in each step, there is a probability that the information will be back to the initial labeled objects. The class probability of each object changes over time during iterations. As the result, the steady-state probability can be obtained. Here, we set up a global equation in (1) for objects according to the Markov chain on the MIML data. The affinities among objects have already been captured in (1). The solution of (1) is the steady-state probabilities which directly provide ranking of labels to indicate the importance of a set of labels to an object.

In the next subsection, we show an example to demonstrate the proposed method.

3.4 An example

We construct a synthetic MIML data set in Fig. 3 to show the calculation and demonstrate the computational procedure of the proposed model. In this example, we generate four objects of each containing two instances. There are four classes in this example, see Table 1.

Table 1 An example of four objects, eight instances, and four classes

For this data set, we set the Euclidean distance metric between two instances $||x^{(i)}_s, x^{(j)}_t||$ as follows:

$$\begin{aligned} \mathbf{{E}}= \left[ {\begin{array}{rrrrrrrr} {0}&{1}&{1}&{1}&{10}&{10}&{10}&{10} \\ {1}&{0}&{1}&{1}&{10}&{10}&{10}&{10} \\ {1}&{1}&{0}&{1}&{10}&{10}&{10}&{10} \\ {1}&{1}&{1}&{0}&{10}&{10}&{10}&{10} \\ {10}&{10}&{10}&{10}&{0}&{2}&{2}&{2} \\ {10}&{10}&{10}&{10}&{2}&{0}&{2}&{2} \\ {10}&{10}&{10}&{10}&{2}&{2}&{0}&{2} \\ {10}&{10}&{10}&{10}&{2}&{2}&{2}&{0} \\ \end{array}} \right] \end{aligned}$$

We see that the instances $x^{(1)}_1,$ $x^{(2)}_1,$ $x^{(1)}_2,$ $x^{(2)}_2$ are similar, and the instances $x^{(3)}_1,$ $x^{(4)}_1,$ $x^{(3)}_2, x^{(4)}_2$ are also similar. It is clear that the instances $x^{(1)}_1,$ $x^{(2)}_1,$ $x^{(1)}_2,$ $x^{(2)}_2$ are not similar to the instances $x^{(3)}_1,$ $x^{(4)}_1,$ $x^{(3)}_2,$ $x^{(4)}_2.$ By using the above distance metric, we can compute the 8-by-8 affinity matrix $A$ given by $a_{i,j,s,t} = \exp [ - 0.2 ||x^{(i)}_{s} ,x^{(j)}_t ||^2 ].$ In addition, the instance-to-object-relation matrix $\mathbf{{B}}$ is given by

$$\begin{aligned} \mathbf{{B}} = \left[ {\begin{array}{llllllll} {1}&{1}&{0}&{0}&{0}&{0}&{0}&{0} \\ {0}&{0}&{1}&{1}&{0}&{0}&{0}&{0} \\ {0}&{0}&{0}&{0}&{1}&{1}&{0}&{0} \\ {0}&{0}&{0}&{0}&{0}&{0}&{1}&{1} \\ \end{array}} \right]. \end{aligned}$$

It follows that the resulting affinity matrix $\mathbf{B} \mathbf{A} \mathbf{B}^\mathrm{T}$ for objects is given as follows

$$\begin{aligned} \left[ {\begin{array}{llll} {3.6375}&{3.2749}&{0.0000}&{0.0000} \\ {3.2749}&{3.6375}&{0.0000}&{0.0000} \\ {0.0000}&{0.0000}&{2.8987}&{1.7973} \\ {0.0000}&{0.0000}&{1.7973}&{2.8987} \\ \end{array}} \right]. \end{aligned}$$

Because of similarities among some instances, it reflects that Objects 1 and 2 are similar, and Objects 3 and 4 are similar. They should have similar class labels. By normalizing each column of the above matrix, we obtain the transition probability matrix

$$\begin{aligned} \mathbf{Q}= \left[ {\begin{array}{llll} {0.5262}&{0.4738}&{0.0000}&{0.0000} \\ {0.4738}&{0.5262}&{0.0000}&{0.0000} \\ {0.0000}&{0.0000}&{0.6173}&{0.3827} \\ {0.0000}&{0.0000}&{0.3827}&{0.6173} \\ \end{array}} \right] \end{aligned}$$

Objects 1 and 3 are training data, and Objects 2 and 4 are testing data. The prior probability distribution matrix for four class labels $\mathbf{{D}}=[\mathbf{{d}}_1 \mathbf{d}_2 \mathbf{d}_3 \mathbf{d}_4]$ are given as follows:

$$\begin{aligned} \mathbf{{D}} = \left[ {\begin{array}{llll} {1}&{1}&{0}&{0} \\ {0}&{0}&{0}&{0} \\ {0}&{0}&{1}&{1} \\ {0}&{0}&{0}&{0} \\ \end{array}} \right]. \end{aligned}$$

We note that matrix $\mathbf{Q}$ is irreducible and primitive. The solution is unique and the algorithm converges. By using Algorithm 1, we obtain the solution ${\bar{\mathbf{P}}}=[\mathbf{{p}}_1 \mathbf{p}_2 \mathbf{p}_3 \mathbf{p}_4]$ given as follows:

$$\begin{aligned} {\bar{\mathbf{P}}} = \left[ {\begin{array}{llll} {0.5525}&{0.5525}&{0.0000}&{0.0000} \\ {0.4475}&{0.4475}&{0.0000}&{0.0000} \\ {0.0000}&{0.0000}&{0.5634}&{0.5634} \\ {0.0000}&{0.0000}&{0.4366}&{0.4366} \\ \end{array}} \right] \end{aligned}$$

According to $\mathbf{p}_l,$ the probability of an object belonging to the $l$th class is obtained; for instance, Object 2 has the probability 0.4475 belonging to classes 1 and 2, and it has almost zero probability belonging to classes 3 and 4; Object 4 has the probability 0.4366 belonging to classes 3 and 4, but it has almost zero probability belonging to classes 1 and 2. We conclude that classes 1 and 2 are definitely more important than classes 3 and 4 for Object 2, and classes 3 and 4 are definitely more important classes 1 and 2 for Object 4. Therefore, the proposed algorithm can computes ranking of labels their to indicate the importance of a set of labels to an object.

4 Experimental results

 

4.1 Data sets

To evaluate the performance of the proposed Markov-Miml algorithm, we conduct experiments on two benchmark MIML data sets. The first one is the image classification task given in [37] to study the MIML framework.¹ In summary, this data set contains 2,000 scene images taken from five possible class labels (desert, mountains, sea, sunset, and trees) and each image is represented as a bag of 9 instances in 15 dimension using the SBN image bag generator [19]. Another data set is the widely used Reuters-21578 text collection in text categorization.² In summary, this data set contains 2,000 documents with multiple classes and represented as a bag of instances based on the techniques of sliding windows, where each instance corresponds to a text segment enclosed in a sliding window [2]. The description of these two data sets is listed in Table 2. More detailed information on these two data sets can be found in [35]. The text and image data are both preprocessed in our experiments. Each instance is normalized such that its Euclidean norm is equal to 1. Also, we follow the setting in [35], we normalize the image data on each dimension in the range between $[0, 5]$ in the M$^3$ Miml algorithm.

Table 2 The description of image and text data for MIML learning

We compare Markov-Miml with MimlBoost, Miml Svm, M$^3$ Miml. All the comparisons are performed in a computer running a server environment with 2.66GHz CPU and 3.5 GB memory. For MimlBoost and Miml Svm, the optimal parameter settings as reported in [37] are used. More precisely, the rounds of MimlBoost are set to be 25 and the Gaussian kernel parameter of Miml Svm is set to be 0.2. For the M$^3$ Miml algorithm, the value of C (cost parameter) and $\gamma$ of M$^3$ Miml is set to the default value of 1.0 as given in [35]. It is reported in [35] that M$^3$ Miml shows similar performance with $\gamma$ in [0.6, 1.4], and the mean value over this range is used as the default value. The number of iterations to find the solution of dual variables in M$^3$ Miml algorithm by Franke and Wolfe’s method [9] is set to be 10. We also evaluate the performance of $k$-nearest neighbor-type algorithms for MIML learning. By using Ml-knn [34] to replace the Ml Svm used in Miml Svm, we get Miml-knn. Here, Ml-knn is parameterized by the size of neighborhood, and the number of nearest neighbors is set to be 10 which is the recommended value given in [34] to obtain the best performance.

Since MIML algorithms make multi-label prediction, the performance is evaluated by multi-label ranking metrics. Four popular multi-label ranking metrics, namely one-error, coverage, ranking loss, and average precision [24] are used to evaluate the algorithm performance in this paper as follows:

• (1) one-error: This measure evaluates how many times the top-ranked label is not in the set of true labels of the object. Define a classifier $H$ that assigns a single label for an object $X_i$ by $H(X_i)=\arg \max _{l \in \mathcal Y } f(X_i ,l),$ then the one-error is

  $$\begin{aligned} \text{ one-}\text{ error}_S (H) = \frac{1}{m^{\prime \prime }}\sum \limits _{i = m^{\prime }+1}^{m^{\prime }+m^{\prime \prime }} {\left[\left[ {H(X_i ) \notin Y_i } \right]\right]} \end{aligned}$$

  where $\left[\left[ \cdot \right]\right]$ is an indicative function, for any predicate $\pi ,$ let $\left[\left[ \pi \right]\right]$ be 1 if $\pi$ holds and 0 otherwise.

• (2) coverage: This measure evaluates how far we need, on the average, to go down the list of labels in order to cover all the true labels of an object. Formally, it is defined to be

  $$\begin{aligned} {\mathop {\text{ coverage}}}_S (f) = \frac{1}{m^{\prime \prime }}\sum \limits _{i = m^{\prime }+1}^{m^{\prime }+m^{\prime \prime }} \mathop {\max }\limits _{l \in Y_i } \mathrm{rank}_f (X_i ,l) - 1 \end{aligned}$$

• (3) ranking loss: This measure evaluates the average fraction of label pairs that are reversely ordered for the object.

  $$\begin{aligned} \text{ rloss}_S (f) = \frac{1}{m^{\prime \prime }}\sum \limits _{i = m^{\prime }+1}^{m^{\prime }+m^{\prime \prime }} {\frac{1}{{|Y_i ||\bar{Y}_i |}}|\{ (l_1 ,l_2 )|f(X_i ,l_1 ) \le f(X_i ,l_2 ),(l_1 ,l_2 ) \in Y \times \bar{Y}\} } \end{aligned}$$

• (4) average precision: This measure evaluates the average fraction of labels ranked above a particular label $l \in Y$ which actually are in $Y.$ It is a performance originally used in information retrieval area [23]. Formally, it is defined to be

  $$\begin{aligned} {\text{ avgprec}}_S (f) = \frac{1}{m^{\prime \prime }}\sum \limits _{i = m^{\prime }+1}^{m^{\prime }+m^{\prime \prime }} {\frac{1}{{|Y_i |}}\sum \limits _{l \in Y_i } {\frac{{|\{ l^{\prime } \in Y_i |\text{ rank}_f (X_i ,l^{\prime }) \le rank_f (X_i ,l)\} |}}{{\text{ rank}_f (X_i ,l)}}} } \end{aligned}$$

  As for average precision, the bigger the values the better the performance, we report the results of 1-average precision; thus, for all evaluation metric results, the smaller the values the better the performance.

 

4.2 Effect of the restart parameter

In this subsection, we study the performance of different algorithms under 10-fold cross-validation. Figures 4 and 5 show the performance of Markov-Miml algorithm with respect to different values of $\alpha$ (the restart parameter in (1)) for text and image data sets, respectively. We observe from the figures that the curves of all evaluation metrics drop significantly as $\alpha$ increases from range [0.50, 0.91]. But the change of the performance is insensitive in the range [0.92,0.99]. In the following experiments, we do not specifically tuned optimal values of $\alpha$ for the two data sets. We just simply set the value of $\alpha$ to be 0.95.

Fig. 4

The performance of Markov-Miml algorithm (on the text data) with respect to the value of $\alpha$

Fig. 5

The performance of Markov-Miml algorithm (on the image data) with respect to the value of $\alpha$

4.3 Convergence of algorithm

Figure 6 shows the convergence of Markov-Miml algorithm. We see from the figure that the changes of probability matrix $||\mathbf{P}_t - \mathbf{P}_{t-1}||,$ decrease when iteration number increases, and the successive difference after several iterations (text data about 10 iterations and image data about 30 iterations), is less than $10^{-15}$ which is small enough for convergence criterion. The computational time is about a second under the MATLAB implementation for both image and text data sets.

Fig. 6

The convergence of Markov-Miml algorithm. a image data, b text data

4.4 Performance of Markov-Miml

We compare the performance as well as the running time of Markov-Miml with Miml-knn, MimlBoost and Miml Svm. In the experiment, we randomly select 90 % of data as training set and use the remaining 10 % of data as test set. 10 trials (each with a different random seed) are made for the test. The mean as well as standard deviation of each compared methods over the same 10 trials are reported.

The main computational cost and storage of the proposed algorithm is to build and store the whole transition probability matrix $\mathbf{Q}.$ In the implementation, we figure out that there are many entries of the affinity matrix $\mathbf{A}$ being close to zero. Therefore, it may not be necessary to store these entries such that both the computational cost of matrix–matrix multiplication and the storage in Algorithm 1 can be reduced. We generate a sparse transition probability matrix $\mathbf{A}$ as follows:

$$\begin{aligned} a_{i,j,s,t} = \left\{ {\begin{array}{ll} {\exp [{{ - ||x_s^{(i)} ,x_t^{(j)} ||} \mathord {\left. {} \right. } {2\sigma ^2 }}]\mathrm{{,}}}&\quad {\mathrm{{if}}\ x_t^{(j)} \in \mathcal N _k \mathrm{{,}}} \\ {0\mathrm{{,}}}&\quad {\mathrm{{otherwise}}\mathrm{{.}}} \\ \end{array}} \right. \end{aligned}$$

where $\mathcal N _{\kappa }$ is the set of $\kappa$ nearest neighbors of instance $x_s^{(i)}.$ The $\kappa$ nearest neighbors can be efficient searched by using $kd$-tree implementation. In Tables 3 and 4, we test several different values of $\kappa$ (from 50 to 1,500) for the classification performance of the Markov-Miml algorithm.

Table 3 The performance of different algorithms on the text data

Table 4 The performance of different algorithms on the image data

Tables 3 and 4 show the performance of different MIML learning algorithms on the text and image data set, respectively. The results in these two tables can be divided into two parts. The upper part shows how the performance of Markov-Miml varies with different values of $\kappa .$ When $\kappa =$ all, it means the original matrix $\mathbf{Q}$ is used and all the entries are employed. The bottom part shows the results of Miml-knn, Miml Svm, MimlBoost, and M$^3$ Miml algorithms. The value following “$\pm$” gives the standard deviation. We see from Tables 3 and 4 that Markov-Miml consistently achieves highly competitive performance with other MIML learning algorithms across all evaluation metrics and data sets. If we examine the results for each of data set individually, for the results of text data in Table 3, we see that the performance of M$^3$ Miml is better than that of Markov-Miml in terms of one-error and average precision metrics, while Markov-Miml, that is, $k=1{,}000,$ 1,500, and all, is better than that of M$^3$ Miml in terms of coverage and ranking loss metrics. For the results of image data in Table 4, we see that Markov-Miml has the highest overall performance. Moreover, the performance of Markov-Miml is not changed significantly for different values of $\kappa .$

Also, we compare the running time of Markov-Miml with other MIML learning methods in Tables 3 and 4. Markov-Miml with $\kappa =$ all shows that Markov-Miml is slightly slower than Miml-knn and Miml Svm (183.3 seconds vs. 139.0 seconds and 180.0 seconds on the text data), but it is still much faster than M$^3$ Miml and MIMBoost (183.3 seconds vs. 3.60 hours and 60.0 hours on the text data). Moreover, the running time of Markov-Miml decreases when the number of neighbors $\kappa$ decreases. When $\kappa$ is equal to 50, the classification accuracy is still comparable with the other MIML learning methods, but the running times are greatly reduced. Even when $\kappa = 500,$ the running times of Markov-Miml are 67.79 and 149.83 s for text and image MIML data, respectively, which are 2.5 times faster than Miml Svm, and hundreds of times faster than M$^3$ Miml.

In summary, the Markov-Miml algorithm is a good alternative for solving MIML problems by studying classification performance and computational time. According to the results in Tables 3 and 4, a not large value of $\kappa$ (e.g., $\kappa =100$) is a suitable choice in the proposed algorithm in terms of classification and computational time required.

4.5 Effect of size of training data

In this experiment, we test the performance of Markov-Miml algorithm with respect to the number of training examples. We randomly pick up 10, 20, 30, 40, 50, 60, 70, 80 % of the data set as training data. The remaining data set is used for testing data. The performance is measured by averaging 10 trials by randomly selected data using this procedure. In Figs. 7 and 8, the performance of Markov-Miml and other three MIML learning algorithms (Miml-knn, Miml Svm, and M$^3$ Miml) on two data sets, respectively, are reported. Here, we do not test MimlBoost as it is very time-consuming for running MimlBoost in this experiment.

Fig. 7

The performance of different algorithms on the text data with respect to the number of training examples. In each subfigure, the lower value the curve is, the better the performance is

Fig. 8

The performance of different algorithms on the image data with respect to the number of training examples. In each subfigure, the lower value the curve is, the better the performance is

We can see from these figures that Markov-Miml outperforms Miml-knn and Miml Svm in general, especially when only 10 percentage of the data set is employed. For the text data, Markov-Miml achieves one-error improvement of 10 % (0.156 vs. 0.256) compared with Miml Svm and 13 % (0.156 vs. 0.286) compared with Miml-knn. For the image data, Markov-Miml achieves one-error improvement of 8.8 % (0.403 vs. 0.491) compared with Miml Svm and 19.4 % (0.403 vs. 0.597) compared with Miml-knn. Markov-Miml is also competitive with M$^3$ Miml on both text data and image data.

We also compare the running time of different algorithms with varying number of training examples, see Table 5. In the table, the first number and the second number under the column of Markov-Miml algorithm ($\kappa$ = all) refer to the computational time required to construct the Markov transition matrix $\mathbf{Q}$ and to run iteration method for solving the linear system $(1-\alpha ) \mathbf{Q} \mathbf{P} + \alpha \mathbf{D} = \mathbf{P}$ to generate a ranking of labels, respectively. We see that both numbers are not changed when different numbers of training examples are used. Also, the construction of the Markov transition matrix takes significantly more time than the computation of solving linear system. As the total number of objects is the same for different percentages of training examples, the size of $\mathbf{Q}$ is the same and the cost would be the same. We see from the table that the computational time required by Markov-Miml is significantly less than that by M$^3$ Miml. Because we set $\kappa$ = all in the experiments, the computational time required by Markov-Miml is more than those by Miml-knn and Miml Svm.

Table 5 Running time (in seconds) of different algorithms with respect to the number of trained examples

In Figs. 9 and 10, we also show the performance of Markov-Miml varies with respect to different values of $\kappa$ and percentages of training data. For the text data, Markov-Miml is not sensitive to specific setting of $\kappa .$ For the image data, the performance of Markov-Miml is affected for small values of $\kappa$ and small percentages of training data. According to these experimental results, we find that a not large value of $\kappa$ (e.g., $\kappa =100$) is a suitable choice for Markov-Miml in terms of classification and computational time required.

Fig. 9

The performance of Markov-Miml algorithm with various $\kappa$ values on the text data with respect to the number of training examples

Fig. 10

The performance of Markov-Miml algorithm with various $\kappa$ values on the image data with respect to number of training examples

5 Conclusion

In this paper, we have proposed an algorithm (Markov-Miml) to determine the rank of class labels for objects in MIML data. The experimental results have demonstrated that the proposed algorithm is efficient and effective. Here, we point out several possible future works.

• (i) We set values of parameter $\alpha$ empirically in this paper. In order to make use of the proposed algorithm more practically and effectively, this parameter can be learned via training data set by setting an optimization procedure for parameter selection.

• (ii) MIML learning is a general framework considering ambiguity in the input (instance) space and output (label) space. Many real-world problems involving ambiguous objects can be properly formalized under MIML learning. Traditional supervised learning is evidently a degenerated version of MIML learning. Thus, we can consider extending the existing research directions on traditional supervised learning underlying the MIML framework, such as the incremental learning or translated learning in MIML data.

Appendix

Proof of Theorem 1:

By Perron–Frobenius Theorem [22], we know that 1 is the spectral radius of $\mathbf{Q},$ that is, 1 is the maximal eigenvalue of $\mathbf{Q}$ in magnitude. The maximal eigenvalue of $(1-\alpha )\mathbf{Q}$ is equal to $1-\alpha .$ It implies that the matrix $I - (1-\alpha ) \mathbf{Q}$ is invertible. Thus, $\mathbf{P} = (I- (1-\alpha ) \mathbf{Q})^{-1} \alpha \mathbf{D}$ is well defined. It shows that there exists a unique matrix $\mathbf{P}$ satisfying $\mathbf{P} = (1-\alpha ) \mathbf{Q} \mathbf{P} + \alpha \mathbf{D}.$ By using the series of expansion of $(I- (1-\alpha ) \mathbf{Q})^{-1}$ as follows:

$$\begin{aligned} \sum _{k=0}^{\infty } (1-\alpha )^k \mathbf{Q}^k \end{aligned}$$

and the fact that the entries of $\mathbf{Q}$ are nonnegative, we have the entries of $\mathbf{P}$ must be nonnegative. We note that when $\mathbf{Q}$ is irreducible, there exists a positive integer $k^{\prime }$ such that the entries $\mathbf{Q}^k \mathbf{D}$ are even positive. Because $\sum _{k=0}^{\infty } (1-\alpha )^k \alpha = 1$ and each column of $\mathbf{Q}^k \mathbf{D}$ consists of $N$ probability distribution vectors, the results follows.

Note that $\mathbf{P}_t - \mathbf{P} = ((1-\alpha ) \mathbf{Q}) ( \mathbf{P}_{t-1} - \mathbf{P} ),$ and the spectral radius of $(1-\alpha )\mathbf{Q}$ is less than 1. The sequence converges for any initial starting vector $\mathbf{P}_0$ satisfying the required property in the theorem. $\square$