Minimizing response time in time series classification

Abstract

Providing a timely output is one of the important criteria in applications of time series classification. Recent studies have been motivated to explore models of early prediction, prediction based on truncated temporal observations. The truncation of input improves the response time, but generally reduces the reliability of the prediction. The trade-off between the earliness and the accuracy is an inherent challenge of learning an early prediction model. In this paper, we present an optimization-based approach for learning an ensemble model for timely prediction with an intuitive objective function. The proposed model is comprised of time series classifiers with different response time, and a sequential aggregation procedure to determine the single timing of its output. We formalize the training of the ensemble classifier as a quadratic programming problem and present an iterative algorithm which minimizes an empirical risk function and the response time required to achieve the minimal risk simultaneously. We conduct an empirical study using a collection of behavior and time series datasets to evaluate the proposed algorithm. In the comparisons of the traditional and time-sensitive performance measures, the ensemble framework showed significant advantages over the existing methods on early prediction.

Appendices

Appendix 1: Proofs of theorems

1.1 Proof of Theorem 1

Proof

For any given $\varTheta$, the smallest sum of $\xi _{t,k}$ gives the largest violation among all $Z\in \mathbf {Z}$. That is,

$$\begin{aligned} \mathop {\min }\frac{C}{\eta }\sum _{t,k}\xi _{t,k}= & {} \mathop {\max }\frac{C}{\eta }\sum _{t,k} z_{t,k}\left( \theta _k-y_t(\mathbf {w}_k^*{}^\top \mathbf {v}_t)\right) \\= & {} \xi ^*+\max {V}(Z,\varTheta ) \end{aligned}$$

Since the largest $V(Z,\varTheta )$ is given by the optimal solution, Problem 4 can be viewed as an optimization problem for the loss $V(Z,\varTheta )$, regularized by the sum of the scaled margins.

Given that $\mathbf {w}^*$ is fixed, $\xi _{t,k}$ can be minimized individually.

$$\begin{aligned} \mathop {\min }\limits _{Z}\sum _{t,k}\xi _{t,k}= \sum _{t,k}\mathop {\max }\limits _{Z}z_{t,k}\left( \theta _k-y_t(\mathbf {w}_k^*{}^\top \mathbf {v}_t)\right) \end{aligned}$$

When $\mathbf {v}_k(t)$ is correctly classified, $\xi _{t,k}$ reduces to 0. It is, thus, constrained by (17) that $z_{j,t}$ is 0 for all $j>k$, ensuring that the solution $Z^*$ is feasible.

1.2 Proof of Theorem 2

Proof

For every $\mathbf {w}$, the smallest feasible $\xi$ for Problem 3 is the maximum violation over $\mathbf {Z}$. That is,

$$\begin{aligned} {\min }C\xi =\mathop {\max }\limits _{Z\in \mathbf {Z}}C\sum _{t,k}\frac{1}{\eta } \left( z_{t,k}\theta _k-z_{t,k}y_i(\mathbf {w}_k^\top \mathbf {v}_t)\right) \end{aligned}$$

(21)

At fixed $\mathbf {w}$ and $\varTheta$, the summation in (21) can be taken individually for each $k$, that is,

$$\begin{aligned} {\min }C\xi= & {} C\sum _{k}\mathop {\max }\limits _{Z\in \mathbf {Z}} \frac{1}{\eta }\sum _{t=1}^\eta \left( z_{t,k}\theta _k-z_{t,k}y_t(\mathbf {w}_k^\top \mathbf {v}_t)\right) \\= & {} C\sum _{k=1}^\lambda \xi _k^* \end{aligned}$$

It follows that for any $\mathbf {w}=(\mathbf {w}_1,\ldots ,\mathbf {w}_\lambda )$, the objective values of Problems 3 and 5 are equivalent with the optimal $\xi$ and $\{\xi _k\}_{k=1}^\lambda$. Subsequently, their minima are equivalent as well.

1.3 Proof of Theorem 3

Proof

Problem 4 maximizes $V(Z,\varTheta )$ and subsequently its first term in (14),

$$\begin{aligned} \xi '=\frac{1}{\eta }\sum _{t,k}z_{t,k}\left( \theta _k-y_t(\mathbf {w}_k^*{}^\top \mathbf {v}_t)\right) \end{aligned}$$

From (13), $\xi '$ is the minimum slack needed to satisfy all constraints of Problem 3 for the tentative $\mathbf {w}$. Upon the convergence of $V(Z,\varTheta )$, $\mathbf {w}$ is, therefore, the optimal solution of Problem 3 for the tentative $\varTheta$. If $(Z,\varTheta )$ is locally optimal for the tentative $\mathbf {w}$, the solution to Problem 4 is identical to $Z$ in the integer domain.

For the objective to improve in each iteration, it suffices that the constraint corresponding to the newly added $Z$ is violated by the tentative solution and satisfied by the desired solution. In Problem 4, (17) constrains $z_{t,k}$ to 0 when the margin for $\mathbf {v}_k(t)$ is above the threshold. Conversely, among the elements of $Z$, only those corresponding to incorrectly classified instances take nonzero values. When substituting such $Z$ into (13), the left-hand side of the inequality becomes the average margin for such instances and violates the tentative upper-bound. Meanwhile, the solution which gives the correct prediction at earliest possible timing can trivially satisfy (13).

Appendix 2: Adopted optimization procedures

This section describes the optimization procedures we adopted from existing algorithms for addressing subproblems in the proposed method.

Problem 5 is a quadratic programming problem for training a linear SVM. In our experiment, we adopted the algorithm from [20] and used an implementation described in Algorithm 3.

Next, we describe the outline of the Interior Point Method we implemented for solving Problem 4. First, Problem 4 is reformulated into a centering problem of the following form.

$$\begin{aligned} \mathop {\min }\limits _Xpf(X)-\sum _{t,k}\log (-g_{t,k}(X))-\sum _{j=1}^k\log (-h_j(X)) \end{aligned}$$

(22)

where variable $X$ represents the parameters and $f$ is the objective function of Problem 4, i.e.,

$$\begin{aligned} f(X)=\sum _k\theta _k^2+\frac{C}{\eta }\sum _{t,k}\xi _{t,k} \end{aligned}$$

while $g$ and $h$ are barrier functions converted from the inequality constraints (16) and (17), respectively.

$$\begin{aligned} \begin{matrix} g_{t,k}=z_{t,k}y_t(\mathbf {w}_k^\top \mathbf {v}_t)-z_{t,k}\theta _k+\xi _{t,k},&h_j=\xi {t,j-1}-z_{t,j} \end{matrix} \end{aligned}$$

The first term in (22), $pf(X)$ can be interpreted as the potential of a force field $F(X)=-t\nabla {f}(X)$, and similarly, $-\log (-g_{t,k}(X))$ and $-\log (-h_j(X))$ the potentials of force fields $G_{t,k}(X)=\frac{1}{g(X)}\nabla {g}(X)$ and $H_{j}(X)=\frac{1}{h(X)}\nabla {h}(X)$, respectively.

Let $X_p^*$ denote the solution of the centering problem for a given $p$. The forces are balanced at $X_p^*$ such that

$$\begin{aligned} F(X^*_p)+\sum \limits _{t,k}G(X^*_p)+\sum _jH(X^*_p)=0 \end{aligned}$$

The barrier method in the following procedure approaches the minimum of the original problem by moving along the balancing center of the force fields by iteratively updating $t$ [9].

Appendix 3: Baseline methods

1.1 Early Classification of Time Series

The state-of-the-art ECTS method [41] is an extension of the nearest neighbor algorithm which constructs the nearest neighbor rules using the prefix, i.e., the truncated segments, of the time series. The prefix of a test instance is classified using the prefixes of the training instances of the same lengths.

ECTS has a set of parameters called the minimum prediction lengths (MPL), assigned to each training instance. The MPL adds a restriction on the nearest neighbor rule regarding the number of observed points so as to avoid premature errors. The restriction is that a prefix of a test instance can be classified only when the $MPL$ of the nearest training instance is smaller than its length. The MPL of each training instance is determined by testing a condition of consistency of called serial on the class clusters in the single-linkage clustering of training data.

ECTS can be directly applied to the early window classification problem which is the special case of the early prediction problem. The prediction window of ECTS is naturally given by the smallest prediction window in $\fancyscript{L}$ that is larger than $MPL$. ECTS is subject to overfitting to noise due to its dependence on the nearest neighbor rule, as noted in [41]. It has a parameter $MinSup$ which can be adjusted to control overfitting, and $MinSup=0$ is suggested when there is no risk. In our empirical study, we presumed the risk of overfitting and tested the values $\{5,10,20\}$ for $MinSup$. The performances were similar among these values.

1.2 Empirical thresholding

Empirical Thresholding [34] is a meta-learning framework for cost-sensitive classification. ET combines an existing classifier with an empirically learned threshold parameter to make a prediction.

ET uses the scores of an external classifier to make a meta-prediction with the minimal cost given the classifier. It is assumed that the problem is a binary classification and the output of the classifier is the numerical score which reflects the likelihood that each instance is assigned to the positive class. The training of a ET model requires a training set and a validation set. The classifier is trained with the training data, the scores over the validation data are computed, and a threshold for minimizing the cost is chosen. To select $\theta$ for an ensemble of classifiers, it requires a combinatorial search of an exponential order.

In order to train a classifier $f$ and a corresponding threshold $\theta$, ET conducts a $p$-fold cross-validation using the training data. The training data are divided into $p$ pairs of training and validation sets. $f$ is learned from each training set, the cost is evaluated over the validation set with all candidates of $\theta$, and those achieving the least cost are chosen.

For our empirical study, we construct an ensemble of classifiers for early window classification using ET. A set of classifiers $\{f_k\}_{k=1}^\lambda$ are trained individually, and a threshold $\theta _k$ is chosen for each $k$. Choosing a combination of $k$ thresholds by cross-validation is infeasible as the order of the grid search is exponential. Alternatively, we implemented ET to choose one threshold in a step in the ascending order of the prediction window $\ell _k$. At step $k$, one chooses $\theta _k$ while the values of $\{\theta _{k'}:k'<k\}$ are fixed to those chosen in prior steps. $\{\theta _{k'}:k'<k\}$ are fixed to the values such that their predictions are reserved for all instances. In our empirical study in Sect. 5.6, the error rate is employed as the cost when evaluating the standard performance measures, and AER is used as the cost when evaluating the adjusted measures.

Appendix 4: Performance measure comparisons

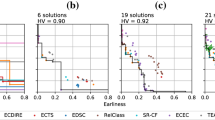
Figure 7 illustrates the error, rejection, and adjusted error rates of GET, which were excluded from Fig. 7a, b in Sect. 5.7. The rejection rate is much smaller, and the error and adjusted error rates are on a significantly larger scale than the other two.

Fig. 7

Performance measure comparisons with GET. a Control Chart, b CBF