Abstract
Local community detection, which aims to find a target community containing a set of query nodes, has recently drawn intense research interest. The existing local community detection methods usually assume all query nodes are from the same community and only find a single target community. This is a strict requirement and does not allow much flexibility. In many real-world applications, however, we may not have any prior knowledge about the community memberships of the query nodes, and different query nodes may be from different communities. To address this limitation of the existing methods, we propose a novel memory-based random walk method, MRW, that can simultaneously identify multiple target local communities to which the query nodes belong. In MRW, each query node is associated with a random walker. Different from commonly used memoryless random walk models, MRW records the entire visiting history of each walker. The visiting histories of walkers can help unravel whether they are from the same community or not. Intuitively, walkers with similar visiting histories are more likely to be in the same community. Moreover, MRW allows walkers with similar visiting histories to reinforce each other so that they can better capture the community structure instead of being biased to the query nodes. We provide rigorous theoretical foundations for the proposed method and develop efficient algorithms to identify multiple target local communities simultaneously. Comprehensive experimental evaluations on a variety of real-world datasets demonstrate the effectiveness and efficiency of the proposed method.












Similar content being viewed by others
Change history
11 October 2019
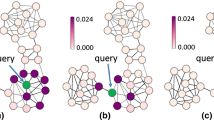
In the published article, Figure 9(a) and Figure 9(b) are the same figure.
Notes
The Lambert-W function is a transcendental function defined by solutions of the equation \(W(x)e^{W(x)}=x\). For real values of the argument, x, it has two branches, \(W_0\) and \(W_{-1}\), the principal and the negative branches [11].
The functionalities of the Brodmann areas can be obtained from http://www.fmriconsulting.com/brodmann/Interact.html.
References
Ahn Y-Y, Ahnert SE, Bagrow JP, Barabási A-L (2011) Flavor network and the principles of food pairing. Sci Rep 1:196
Akakin HC, Gurcan MN (2012) Content-based microscopic image retrieval system for multi-image queries. IEEE Trans Inf Technol Biomed 16(4):758–769
Akbas E, Zhao P (2017) Truss-based community search: a truss-equivalence based indexing approach. Proc VLDB Endow 10(11):1298–1309
Akoglu L, Chau DH, Vreeken J, Tatti N, Tong H, Faloutsos C (2013) Mining connection pathways for marked nodes in large graphs. In: SDM
Alamgir M, Von Luxburg U (2010) Multi-agent random walks for local clustering on graphs. In: ICDM
Andersen R, Chung F, Lang K (2006) Local graph partitioning using pagerank vectors. In: FOCS
Andersen R, Lang KJ (2006) Communities from seed sets. In: WWW
Bagrow JP, Bollt EM (2005) Local method for detecting communities. Phys Rev E 72(4):046108
Baranzini SE, Galwey NW, Wang J et al (2009) Pathway and network-based analysis of genome-wide association studies in multiple sclerosis. Human Mol Genet 18(11):2078–2090
Barbieri N, Bonchi F, Galimberti E, Gullo F (2015) Efficient and effective community search. Data Min Knowl Discov 29(5):1406–1433
Barry D, Parlange J-Y, Li L, Prommer H, Cunningham C, Stagnitti F (2000) Analytical approximations for real values of the lambert w-function. Math Comput Simul 53(1):95–103
Benson AR, Gleich DF, Leskovec J (2015) Tensor spectral clustering for partitioning higher-order network structures. In: SDM
Bian Y, Ni J, Cheng W, Zhang X (2017) Many heads are better than one: local community detection by the multi-walker chain. In: ICDM
Bian Y, Ni J, Cheng W, Zhang X (2019) The multi-walker chain and its application in local community detection. Knowl Inf Syst 60(3):1663–1691
Cho D-Y, Kim Y-A, Przytycka TM (2012) Network biology approach to complex diseases. PLoS Comput Biol 8(12):e1002820
Clauset A (2005) Finding local community structure in networks. Phys Rev E 72(2):026132
Crossley NA, Mechelli A, Vértes PE, Winton-Brown TT, Patel AX, Ginestet CE, McGuire P, Bullmore ET (2013) Cognitive relevance of the community structure of the human brain functional coactivation network. Proc Natl Acad Sci 110:11583–11588
Cui W, Xiao Y, Wang H, Lu Y, Wang W (2013) Online search of overlapping communities. In: SIGMOD, pp 277–288
Fang Y, Cheng R, Li X, Luo S, Hu J (2017) Effective community search over large spatial graphs. Proc VLDB Endow 10(6):709–720
Fortunato S (2010) Community detection in graphs. Phys Rep 486(3–5):75–174
He K, Shi P, Hopcroft JE, Bindel D (2016) Local spectral diffusion for robust community detection. In: 12th workshop on mining and learning with graphs
He K, Sun Y, Bindel D, Hopcroft J, Li Y (2015) Detecting overlapping communities from local spectral subspaces. In: ICDM
Huang X, Cheng H, Qin L, Tian W, Yu JX (2014) Querying k-truss community in large and dynamic graphs. In: SIGMOD
Huang X, Lakshmanan LV, Xu J (2017) Community search over big graphs: Models, algorithms, and opportunities. In: ICDE
Huang X, Lakshmanan LV, Yu JX, Cheng H (2015) Approximate closest community search in networks. Proc VLDB Endow 9(4):276–287
Kloster K, Gleich DF (2014) Heat kernel based community detection. In: KDD
Kloumann IM, Kleinberg JM (2014) Community membership identification from small seed sets. In: KDD
Kong X, Yu PS (2014) Brain network analysis: a data mining perspective. ACM SIGKDD Explor Newsl 15(2):30–38
Lee C, Jang W-D, Sim J-Y, Kim C-S (2015) Multiple random walkers and their application to image cosegmentation. In: CVPR
Lee S-H, Jang W-D, Park BK, Kim C-S (2016) Rgb-d image segmentation based on multiple random walkers. In: ICIP
Li Y, He K, Bindel D, Hopcroft JE (2015) Uncovering the small community structure in large networks: a local spectral approach. In: WWW
Newman ME (2001) The structure of scientific collaboration networks. Proc Natl Acad Sci 98(2):404–409
Ruchansky N, Bonchi F, García-Soriano D, Gullo F, Kourtellis N (2015) The minimum wiener connector problem. In: SIGMOD
Ruchansky N, Bonchi F, Garcia-Soriano D, Gullo F, Kourtellis N (2017) To be connected, or not to be connected: that is the minimum inefficiency subgraph problem. In: CIKM
Shan J, Shen D, Nie T, Kou Y, Yu G (2016) Searching overlapping communities for group query. World Wide Web 19(6):1179–1202
Spielman DA, Teng S-H (2013) A local clustering algorithm for massive graphs and its application to nearly-linear time graph partitioning. SIAM J Comput 42(1):1–26
Tong H, Faloutsos C (2006) Center-piece subgraphs: problem definition and fast solutions. In: KDD
Tong H, Faloutsos C, Pan J-Y (2006) Fast random walk with restart and its applications. In: ICDM
Wang K, Li M, Hakonarson H (2010) Analysing biological pathways in genome-wide association studies. Nat Rev Genet 11(12):843
Whang JJ, Gleich DF, Dhillon IS (2013) Overlapping community detection using seed set expansion. In: CIKM
Wu Y, Bian Y, Zhang X (2016) Remember where you came from: on the second-order random walk based proximity measures. Proc VLDB Endow 10(1):13–24
Wu Y, Jin R, Li J, Zhang X (2015) Robust local community detection: on free rider effect and its elimination. In: VLDB
Wu Y, Zhang X, Bian Y, Cai Z, Lian X, Liao X, Zhao F (2018) Second-order random walk-based proximity measures in graph analysis: formulations and algorithms. VLDB J 27(1):127–152
Xia M, Wang J, He Y (2013) Brainnet viewer: a network visualization tool for human brain connectomics. PLoS ONE 8(7):e68910
Yan Y, Bian Y, Luo D, Lee D, Zhang X (2019) Constrained local graph clustering by colored random walk. In: The world wide web conference, pp 2137–2146
Yang J, Leskovec J (2012) Defining and evaluating network communities based on ground-truth. In: ICDM
Yin H, Benson AR, Leskovec J, Gleich DF (2017) Local higher-order graph clustering. In: KDD
Yuan L, Qin L, Zhang W, Chang L, Yang J (2018) Index-based densest clique percolation community search in networks. TKDE 30(5):922–935
Zhou D, Zhang S, Yildirim MY, Alcorn S, Tong H, Davulcu H, He J (2017) A local algorithm for structure-preserving graph cut. In: KDD
Acknowledgements
This work was partially supported by the National Science Foundation grants IIS-1664629 and CAREER.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 More theoretical results of the visiting history vector
In this section, we first show that the visiting history vector \(\mathbf {v}^{(t)}\) (we omit the subscript “i” for simplicity) is a weighted sum of \(\mathbf {e}^{(\tau )}(1\le \tau \le t)\). Then we provide a tighter error bound on \(\Vert \mathbf {v}^{(t+1)}-\mathbf {v}^{(t)}\Vert _1\). These results are used in the speeding-up strategies introduced in Sect. 5.
1.1.1 Expansion of the visiting history vector
We expand the visiting history vector \(\mathbf {v}^{(t)}\) into a linear combination of vectors \(\mathbf {e}^{(\tau )}(0\le \tau \le t)\) and show that \(\mathbf {v}^{(t)}\) is stochastic.
Theorem 4
Based on Eq. (3), for \(K\ge 1\) and \(t\ge 1\), we have
where
and
Please refer to Appendix 8.4 for the proof.
Next we show \(\mathbf {v}^{(t)}\) is stochastic. Note that in the following analysis, we use \(\theta ^{(t)}_{\tau }\) to represent \(\theta ^{(t)}_{\tau }(\beta ) \) for simplicity.
Lemma 2
Let \(\varvec{\psi }^{(t)}\) be the column vector \([\psi ^{(t)}_{0},\dots ,\psi ^{(t)}_{t}]^\intercal \). For \(t\ge 1\), \(\varvec{\psi }^{(t)}\) is positive and \(\parallel \varvec{\psi }^{(t)}\parallel _1=1\).
Proof
From Theorem 4, we have \(0<\theta ^{(t)}_{\tau }\le 1\) for \(1\le \tau \le t\) and \(\theta ^{(t)}_{\tau }>\theta ^{(t)}_{\tau '}\) for \(1\le \tau '<\tau \le t\). Thus, \(\varvec{\psi }^{(t)}\) is positive. Furthermore, we have
If \(1\le t\le K\),
If \(t\ge K+1\),
Therefore, \(\parallel \varvec{\psi }^{(t)}\parallel _1=1\). \(\square \)
The stochastic property of \(\mathbf {v}^{(t)}\) can be directly derived from Lemma 2 and Eq. (7) which is summarized in the following theorem.
Theorem 5
For \(t\ge 0\), \(\mathbf {v}^{(t)}\) is nonnegative and \(\parallel \mathbf {v}^{(t)}\parallel _1=1\).
1.1.2 A tighter error bound
Next we provide a tight error bound on \(\parallel \mathbf {v}^{(t+1)}-\mathbf {v}^{(t)}\parallel _1\) to show its fast convergence. Based on Eqs. (8) and (9), when t is large, \(\theta ^{(t)}_{\tau }(\beta )\) and \(\psi ^{(t)}_{\tau }(\beta )\) will be small. For simplicity, in the following analysis, we use \(\theta ^{(t)}_{\tau }\) and \(\psi ^{(t)}_{\tau }\)to represent \(\theta ^{(t)}_{\tau }(\beta ) \) and \(\psi ^{(t)}_{\tau }(\beta )\), respectively. The following theorem first provides some properties of \(\psi ^{(t)}_{\tau }\) regarding t and then gives the error bound on \(\parallel \mathbf {v}^{(t+1)}-\mathbf {v}^{(t)}\parallel _1\).
Theorem 6
-
(i)
When \(t>t_\beta =\log \epsilon /\log \beta \) for a \(\epsilon >0\), we have \(|\psi ^{(t+1)}_{0}-\psi ^{(t)}_{0}|<\epsilon \), \(\psi ^{(t+1)}_{t+1}<\frac{\epsilon }{K}\) and \(|\psi ^{(t+1)}_{\tau }-\psi ^{(t)}_{\tau }|<\frac{\epsilon }{K}\) for \(1\le \tau \le t\).
-
(ii)
\(\parallel \mathbf {v}^{(t+1)}-\mathbf {v}^{(t)}\parallel _1 \le 2\beta ^t(1-\frac{1}{K}\sum \nolimits _{\tau =1}^{K-1}\theta ^{(t)}_{\tau })\)
To prove Theorem 6, we first show some properties of \(\theta ^{(t)}_{\tau }\).
Lemma 3
For \(t\ge \tau \ge 1\), \(t>\tau _0\ge 1\), we have
- (i)
\((1-\theta ^{(t)}_{\tau -1})(1-\beta ^{t-\tau }) = 1 - \theta ^{(t)}_{\tau }\)
- (ii)
\((1-\theta ^{(t)}_{\tau _0})(1-\theta ^{(t-\tau _0)}_{\tau }) = 1 - \theta ^{(t)}_{\tau _0+\tau }\)
Lemma 3 can be directly derived from the definition of \(\theta ^{(t)}_{\tau }\) in Eq. (9). From Lemma 3 we have the following additional properties.
Corollary 1
For \(t\ge \tau \ge 1\), \(t>\tau _0\ge 1\),
- (i)
\(\theta ^{(t)}_{1}=\beta ^{t-1}\); \(\theta ^{(t)}_{t}=1\)
- (ii)
\((1-\theta ^{(t)}_{\tau -1})\beta ^{t-\tau } = \theta ^{(t)}_{\tau } - \theta ^{(t)}_{\tau -1}\)
- (iii)
\((1-\theta ^{(t)}_{\tau _0})\theta ^{(t-\tau _0)}_{\tau } = \theta ^{(t)}_{\tau _0+\tau } - \theta ^{(t)}_{\tau _0}\);
\((1-\theta ^{(t-\tau _0)}_{\tau })\theta ^{(t)}_{\tau _0} = \theta ^{(t)}_{\tau _0+\tau } - \theta ^{(t-\tau _0)}_{\tau }\)
Now we prove Theorem 6.
Proof
(of Theorem 6) Based on the properties of Corollary 1, we have \(\theta ^{(t+1)}_{\tau +1}-\theta ^{(t)}_{\tau }=(1-\theta ^{(t)}_{\tau })\theta ^{(t+1)}_{1}\) for \(t\ge \tau \ge 1\).
Now, we divide the proof into several cases based on the value of \(\tau \).
- (a)
When \(\tau =0\), \(\psi ^{(t)}_{0}=1-\frac{1}{K}\sum \limits _{j=1}^{K}\theta ^{(t)}_{t+1-j}\),
$$\begin{aligned} \psi ^{(t+1)}_{0}-\psi ^{(t)}_{0}=\frac{-1}{K}\sum \limits _{j=1}^{K}(\theta ^{(t+1)}_{t+2-j}-\theta ^{(t)}_{t+1-j})=\frac{-1}{K}\sum \limits _{j=1}^{K}(1-\theta ^{(t)}_{t+1-j})\theta ^{(t+1)}_{1}<0 \end{aligned}$$ - (b)
When \(1\le \tau \le t-K\), \(\psi ^{(t)}_{\tau }=\frac{1}{K}(\theta ^{(t)}_{t+1-\tau }-\theta ^{(t)}_{t+1-K-\tau })\),
$$\begin{aligned} \psi ^{(t+1)}_{\tau }-\psi ^{(t)}_{\tau }&=\frac{1}{K}[(\theta ^{(t+1)}_{t+2-\tau }-\theta ^{(t)}_{t+1-\tau })-(\theta ^{(t+1)}_{t+2-K-\tau }-\theta ^{(t)}_{t+1-K-\tau })]\\&=\frac{1}{K}[(1-\theta ^{(t)}_{t+1-\tau })-(1-\theta ^{(t)}_{t+1-K-\tau })]\theta ^{(t+1)}_{1}\\&=\frac{1}{K}(\theta ^{(t)}_{t+1-K-\tau }-\theta ^{(t)}_{t+1-\tau })\theta ^{(t+1)}_{1}\\&<0 \end{aligned}$$ - (c)
When \(\tau =t-K+1\),
$$\begin{aligned} \psi ^{(t+1)}_{t-K+1}-\psi ^{(t)}_{t-K+1}&=\frac{1}{K}[(\theta ^{(t+1)}_{K+1}-\theta ^{(t+1)}_{1})-\theta ^{(t)}_{K}]\\&=\frac{1}{K}[(1-\theta ^{(t)}_{K})\theta ^{(t+1)}_{1}-\theta ^{(t+1)}_{1}]\\&=-\frac{1}{K}\theta ^{(t)}_{K}\theta ^{(t+1)}_{1}\\&<0 \end{aligned}$$ - (d)
When \(t-K+2\le \tau \le t\), \(\psi ^{(t)}_{\tau }=\frac{1}{K}\theta ^{(t)}_{t+1-\tau }\),
$$\begin{aligned} \psi ^{(t+1)}_{\tau }-\psi ^{(t)}_{\tau }&=\frac{1}{K}(\theta ^{(t+1)}_{t+2-\tau }-\theta ^{(t)}_{t+1-\tau })\\&=\frac{1}{K}(1-\theta ^{(t)}_{t+1-\tau })\theta ^{(t+1)}_{1}\\&>0 \end{aligned}$$ - (e)
When \(\tau =t+1\), \(\psi ^{(t+1)}_{t+1}=\frac{1}{K}\theta ^{(t+1)}_{1}\).
For statement (i) in Theorem 6, when \(t>t_\beta =\log \epsilon /\log \beta \), \(\theta ^{(t+1)}_{1}=\beta ^t<\epsilon \), so \(|\psi ^{(t+1)}_{0}-\psi ^{(t)}_{0}|<\epsilon \), \(\psi ^{(t+1)}_{t+1}<\frac{\epsilon }{K}\) and \(|\psi ^{(t+1)}_{\tau }-\psi ^{(t)}_{\tau }|<\frac{\epsilon }{K}\) for \(1\le \tau \le t\).
For statement (ii), since \(\mathbf {v}^{(t)} =\sum \nolimits _{\tau =0}^{t}\psi ^{(t)}_{\tau }\mathbf {e}^{(\tau )}\), we have
\(\square \)
1.2 The Proof of Theorem 2
In the following proof, we omit the subscript “i” for simplicity.
Proof
where \({\Delta }^{(\tau +1)}=\Vert \mathbf {x}^{(\tau +1)}-\mathbf {x}^{(\tau )}\Vert _1\).
From Lemma 1, we know that
If \(\alpha \ne \beta \), let \(c=\max \{\alpha ,\beta \}\), then
Since \(t_\beta =\log _\beta \epsilon \), we have \(\alpha ^{t_\beta }=\epsilon ^{\log _\beta \alpha }\) and \(\beta ^{t_\beta }=\epsilon \), then \(c^{t_\beta }=O(\epsilon ^{\min \{1,\log _\beta \alpha \}})\)
As a result, if \(\alpha \ne \beta \), \(\Vert \mathbf {x}^{(t)}-\mathbf {x}^{(t_\beta )}\Vert _1=O(\epsilon ^{\min \{1,\log _\beta \alpha \}})\).
If \(\alpha =\beta \), we have
Therefore, \(\Vert \mathbf {x}^{(t)}-\mathbf {x}^{(t_\beta )}\Vert _1=O(\epsilon |\log \epsilon |)\) if \(\alpha =\beta \). \(\square \)
1.3 Convergence property of the reinforcement process
In this section, we show the convergence property of \(\mathbf {x}_i^{(t)}\).
Theorem 7
\(\lim \nolimits _{t\rightarrow \infty } \Vert \mathbf {x}_i^{(t+1)}-\mathbf {x}_i^{(t)}\Vert _1 = 0\) for \(q_i\in Q\).
Proof
From \(\mathbf {x}_i^{(t-1)}\) to \(\mathbf {x}_i^{(t)}\), there are two steps: (1) form \(\mathbf {x}_i^{(t-1)}\) to \(\mathbb {x}_i^{(t-1)}\) based on Eq. (6), and (2) from \(\mathbb {x}_i^{(t-1)}\) to \(\mathbf {x}_i^{(t)}\) based on Eq. (2).
In the first step, we can rewrite Eq. (6) as \(\mathbb {x}_i^{(t-1)}={\mathbb {Q}_i^{(t-1)}}^\intercal \mathbf {x}_i^{(t-1)}\), where
and \(\mathbf {y}_{i}^{(t)}=\sum \nolimits _{j=1}^S\mathbf {R}^{(t)}(j,i)\mathbf {x}_{j}^{(t)}\). We know that \({\mathbf {y}_{i}^{(t)}}^\intercal \mathbf {1}=1\).
In the second step, we can rewrite Eq. (2) as \(\mathbf {x}_i^{(t)}={\mathbb {P}_i^{(t)}}^\intercal \mathbb {x}_i^{(t-1)}\), where \(\mathbb {P}_i^{(t)}=\alpha \mathbf {P}+(1-\alpha )\mathbf {1}{\mathbf {v}_i^{(t-1)}}^\intercal \). According to Eq. (3), after a enough long time \(\tau _1\), for \(t>\tau _1\), \(\mathbf {v}_i^{(t)}\) will converge, so will \(\mathbb {P}_i^{(t)}\). Let \(\mathbb {P}_i\) denote the converged \(\mathbb {P}_i^{(t)}\).
As a result, \(\mathbf {x}_i^{(t)}=\mathbb {P}_i^\intercal \mathbb {x}_i^{(t-1)}=[\mathbb {Q}_i^{(t-1)}\mathbb {P}_i]^\intercal \mathbf {x}_i^{(t-1)}\) and \(\mathbb {Q}_i^{(t-1)}\) and \(\mathbb {P}_i\) are stochastic, i.e., \(\mathbb {Q}_i^{(t-1)}\mathbf {1}=\mathbb {P}_i\mathbf {1}=\mathbf {1}\).
Since the reinforcement process is a dynamic process between time points 0 and t, we can construct a graph to record the intermediate steps as follows. If at certain time point \(\tau \) (\(0\le \tau \le t\)), the score vectors of \(q_i\) and \(q_j\) have positive similarity (bigger than a very small threshold, e.g., 0.01), then there is an edge between them. In this graph, if a node \(q_i\) is isolated, that means the score vector of \(q_i\) has no positive similarity (bigger than a very small threshold, e.g., 0.01) with the score vector of any other query node at all time. Its convergence is guaranteed according to Theorem 1.
Let \(Q'\) represent the node set of any other connected component containing at least 2 nodes. For a query node \(q_i\in Q'\), let \(T=\{\tau |\sum \nolimits _{q_j\in Q'}\mathbf {R}^{(\tau )}(j,i)=0\}\). Then for \(\tau \in T\), \(\mathbb {Q}_i^{(\tau )}=\mathbf {I}\). Note that \(T\ne \emptyset \), since we have \(\mathbb {Q}_i^{(0)}=\mathbf {I}\). Next we extend \(\mathbf {x}_i^{(t)}\).
Based on the Perron–Frobenius theorem, after a enough long time \(\tau _2\), for \(t>\tau _2\), \(\mathbb {P}_i^t=\mathbf {1x}_i^\intercal \), i.e., the row vectors of \(\mathbb {P}_i^t\) will be an identical vector \(\mathbf {x}_i^\intercal \) [13]. We set \(\tau _0 = \max \{\tau _1,\tau _2\}\). Then when \(t>\tau _0\), we have
Next we check the difference between \(\mathbf {x}_i^{(t+1)}\) and \(\mathbf {x}_i^{(t)}\).
Since after \(t_c\) steps, \(\mathbf {R}^{(t)}\) does not change, we have
Let \(\Delta ^{(t+1)}=\max _{q_j\in {Q'}}\Delta _j^{(t+1)}\), we have
Let \(\Delta '^{(t+1)}=\gamma \sum \nolimits _{k=1}^{\tau _0}(1-\gamma )^{k-1}\Delta ^{(t+1-k)}\), we have \(\Delta ^{(t+1)}<\Delta '^{(t+1)}\). Moreover,
Thus, for any \(q_i\in Q'\), \(\lim \nolimits _{t\rightarrow \infty }\Delta _i^{(t)}=\lim \nolimits _{t_\rightarrow \infty }\Delta ^{(t)}=\lim \nolimits _{t_\rightarrow \infty }\Delta '^{(t)}=0\). \(\square \)
1.4 The Proof of Theorem 4
Proof
We use induction to prove
When \(t=1\), based on Eq. (3) and \(\mathbf {v}^{(0)}=\mathbf {e}^{(0)}\), we have
On the other hand, based on Eq. (11), we have
Suppose that for \(t\ge 1\), Eq. (11) holds. Now we check \(\mathbf {v}^{(t+1)}\). When \(1\le t\le K-2\),
Since \( t\le K-2\), then for \(1\le \tau \le t\), \(\theta ^{(t)}_{t+1-K-\tau }=0 \). Next, based on Eq. (11),
According to Corollaries 1 (i) and (iii), we have \(\beta ^t=\theta ^{(t+1)}_{1}\) and \((1-\theta ^{(t+1)}_{1})\theta ^{(t+1-1)}_{t+1-\tau }=\theta ^{(t+1)}_{t+2-\tau }-\theta ^{(t+1)}_{1}\) for \(1\le \tau \le t\). Then we substitute \(\mathbf {v}^{(t)}\) into \(\mathbf {v}^{(t+1)}\).
This means when \(1\le t\le K-1\), Eq. (11) holds. In the following inductive steps, we check \(\mathbf {v}^{(t+1)}\) for \(t\ge K-1\).
Based on Eq. (3), we have
If \(t-K+1\le \tau \le t\), then \(\theta ^{(t)}_{t+1-K-\tau }=0\). Now we divide the second term into two parts: \(1\sim (t-K)\) and \((t-K+1)\sim t\).
Since when \(t-K+2\le \tau \le t+1\), \(\theta ^{(t+1)}_{t+2-K-\tau }=0\), we can combine the last two items to get
Therefore, when \(t\ge 1\), Eq. (11) is always valid. \(\square \)
Rights and permissions
About this article
Cite this article
Bian, Y., Luo, D., Yan, Y. et al. Memory-based random walk for multi-query local community detection. Knowl Inf Syst 62, 2067–2101 (2020). https://doi.org/10.1007/s10115-019-01398-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-019-01398-3