Spike coding from the perspective of a neurone

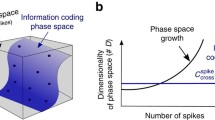
Abstract

In this paper, we compare existing methods for quantifying the coding capacity of a spike train, and review recent developments in the application of information theory to neural coding. We present novel methods for characterising single-unit activity based on the perspective of a downstream neurone and propose a simple yet universally applicable framework to characterise the order of complexity of neural coding by single units. We establish four orders of complexity in the capacity for neural coding. First-order coding, quantified by firing rates, is conveyed by frequencies and is thus entirely described by first moment processes. Second-order coding, represented by the variability of interspike intervals, is quantified by the log interval entropy. Third-order coding is the result of spike motifs that associate adjacent inter-spike intervals beyond chance levels; it is described by the joint interval histogram, and is measured by the mutual information between adjacent log intervals. Finally, nonstationarities in activity represent coding of the fourth-order that arise from the effects of a known or unknown stimulus.

Appendix

The entropy of a gamma probability density function

Consider a gamma probability density function ${\mathcal{G}}(\alpha, \beta)$ expressed with respect to time w, using α and β as shaping and scaling parameters, respectively.

$${\mathcal{G}}(\alpha, \beta) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} w^{\alpha-1} {\text{e}}^{-w/\beta} $$

(52)

where the gamma function Γ(α) is given by a definite integral expressed with respect to z over its support set ${\mathcal{S}}_Z$ defined over the interval [0, ∞].

$$\Gamma (\alpha) = \int\limits_{{\mathcal{S}}_Z} z^{\alpha - 1} {\text{e}}^{-z} {\text{d}}z $$

(53)

It is possible to estimate α and β from the first two moments (Wadsworth 1990), but precise values can only be obtained using computational algorithms such as maximum likelihood estimation (Mann et al. 1974; Gross and Clark 1975). By substituting the gamma probability density function for f _w (w|I) into Eq. 8, the differential entropy s[w] can be expressed in ‘nats’.

$$s[{\mathbf{w}}] = -\int\limits_{{\mathcal{S}}_W} {\mathcal{G}} (\alpha, \beta) \log_e {\mathcal{G}} (\alpha, \beta) {\text{d}}w $$

(54)

$$s[{\mathbf{w}}] = -\int\limits_{{\mathcal{S}}_W} {\mathcal{G}} (\alpha, \beta) \log_e \left(\frac{1}{\beta^{\alpha} \Gamma (\alpha)}w^{\alpha-1} {\text{e}}^{-w/\beta} \right) {\text{d}}w $$

(55)

$$s[{\mathbf{w}}] = -\left(-\alpha \log_e \beta - \log_e \Gamma (\alpha) + (\alpha - 1) E(\log_e w) - \frac{E(w)}{\beta} \right) $$

(56)

For a gamma probability density function ${\mathcal{G}} (\alpha, \beta),$ the expectation E(w) is given by αβ (Papoulis and Pillia 2002).

$$s[{\mathbf{w}}] = \alpha \log_e \beta + \log_e \Gamma (\alpha) - (\alpha - 1) E(\log_e w) + \alpha $$

(57)

The expectation term E(log _e w) can be expressed with respect to ${\mathcal{G}}(\alpha, \beta).$

$$E(\log_e w) = \int\limits_{{\mathcal{S}}_W} {\mathcal{G}} (\alpha, \beta) \log_e w{\text{d}}w $$

(58)

$$E(\log_e w) = \int\limits_{{\mathcal{S}}_W} \frac{1}{\beta^{\alpha} \Gamma (\alpha)} w^{\alpha-1} {\text{e}}^{-w/\beta} \log_{e} w {\text{d}}w $$

(59)

To expand the integral, it is useful to change the variable w for z, where z=w/β, thus w=βz, therefore dw=βdz, and ${\mathcal{S}}_Z$ is defined over the interval [0, ∞].

$$ E(\log_e w) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} \int\limits_{{\mathcal{S}}_Z} (\beta z)^{\alpha-1} {\text{e}}^{-z} \log_{e} (\beta z) \beta {\text{d}}z $$

(60)

$$ E(\log_e w) = \frac{\beta^{\alpha}}{\beta^{\alpha} \Gamma (\alpha)} \int\limits_{{\mathcal{S}}_Z} z^{\alpha-1} {\text{e}}^{-z} (\log_{e} \beta + \log_{e} z) {\text{d}} z $$

(61)

$$ E(\log_e w) = \left(\frac{\log_e \beta}{\Gamma (\alpha)} \int\limits_{{\mathcal{S}}_Z} z^{\alpha-1} {\text{e}}^{-z} {\text{d}}z \right) + \left(\frac{1}{\Gamma (\alpha)} \int\limits_{{\mathcal{S}}_Z} z^{\alpha-1} {\text{e}}^{-z} \log_e z {\text{d}}z \right) $$

(62)

The first integral expression can be substituted with the gamma function expressed in Eq. 53.

$$ E(\log_e w) = \frac{\log_e \beta}{\Gamma (\alpha)} \Gamma (\alpha) + \frac{1}{\Gamma (\alpha)} \int\limits_{{\mathcal{S}}_Z} z^{\alpha-1} {\text{e}}^{-z} \log_e z {\text{d}}z $$

(63)

$$ E(\log_e w) = \log_e \beta + \frac{1}{\Gamma (\alpha)} \int_{{\mathcal{S}}_Z} z^{\alpha-1} {\text{e}}^{-z} \log_e z {\text{d}}z $$

(64)

The remaining integral expression corresponds to the differential of the gamma function, where:

$$ \frac{{\text{d}}}{{\text{d}} \alpha} \Gamma (\alpha) = \int\limits_{{\mathcal{S}}_Z} z^{\alpha - 1} {\text{e}}^{-z} \log_e z {\text{d}}z $$

(65)

Equation 64 can thus be expressed with respect to the differential term:

$$E(\log_e w) = \log_e \beta + \frac{1}{\Gamma (\alpha)} \frac{{\text{d}}}{{\text{d}} \alpha} \Gamma (\alpha)$$

(66)

$$E(\log_e w) = \log_e \beta + \Psi (\alpha)$$

(67)

where the psi function Ψ(α) is the derivative of the log gamma function:

$$\Psi(\alpha) = \frac{{\text{d}}}{{\text{d}} \alpha} \log_e \Gamma(\alpha)$$

(68)

$$\therefore \Psi(\alpha) = \frac{1}{\Gamma (\alpha)} \frac{{\text{d}}\Gamma(\alpha)}{{\text{d}} \alpha}$$

(69)

The expression for E(log _e w) in Eq. 67 can thus be substituted into Eq. 57.

$$s[{\mathbf{w}}] = \alpha \log_e \beta + \log_e \Gamma (\alpha) - (\alpha-1) (\log_e \beta + \Psi (\alpha)) + \alpha $$

(70)

$$s[{\mathbf{w}}] = \alpha \log_e \beta + \log_e \Gamma (\alpha) - \alpha \log_e \beta + \log_e \beta - (\alpha-1) \Psi (\alpha) + \alpha $$

(71)

$$\therefore s[{\mathbf{w}}] = \log_e [ \beta \Gamma (\alpha) ] + (1 - \alpha) \Psi (\alpha) + \alpha $$

(72)

The log interval entropy of a gamma process

First, the probability density function f _x (x|I) of the logarithmic intervals x is expressed with respect to the probability density function f _w (w|I) of the linear intervals w, where w = e^x = dw/dx.

$$ f_{x} (x | I) = f_{w}(w | I) \frac{{\text{d}}w}{{\text{d}}x} $$

(73)

$$ f_{x} (x | I) = f_{w}(w | I) {\text{e}}^{x} $$

(74)

The probability density function ${\mathcal{G}}(\alpha, \beta)$ can be used to represent f _w (w|I) for a gamma process.

$$ f_{x} (x | I) = {\mathcal{G}} (\alpha, \beta) {\text{e}}^{x} $$

(75)

$$\therefore f_{x} (x | I) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} w^{\alpha} {\text{e}}^{-w/\beta} $$

(76)

The entropy s[x] can be expressed by substitution into Eq. 23.

$$ s[{\mathbf{x}}] = -\int\limits_{{\mathcal{S}}_X} {\mathcal{G}} (\alpha, \beta) \log_e \left(\frac{1}{\beta^{\alpha} \Gamma (\alpha)} w^{\alpha} {\text{e}}^{-w/\beta} \right) {\text{d}}x $$

(77)

$$ s[{\mathbf{x}}] = -\left(-\alpha \log_e \beta - \log_e \Gamma (\alpha) + \alpha E(\log w) - \frac{E(w)}{\beta} \right) $$

(78)

For a gamma probability density function ${\mathcal{G}}(\alpha, \beta),$ the expectation E(w) is given by α β (Papoulis and Pillia 2002).

$$ s[{\mathbf{x}}] = \alpha \log_e \beta + \log_e \Gamma (\alpha) - \alpha E(\log w) + \alpha $$

(79)

To express the expectation term E(log w), it is first useful to introduce a new variable y, where y=x−log _e β. Since dy/dx = 1, the probability density function f _y (y|I) is identical to f _x (x|I) as shown in Eq. 76, and may be expressed with respect to y by the substitution x=y + log _e β.

$$f_{y}(y | I) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} w^{\alpha} {\text{e}}^{-w/\beta} $$

(80)

$$f_{y}(y | I) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} {\text{e}}^{\alpha x} {\text{e}}^{-{\text{e}}^{x}/\beta} $$

(81)

$$f_{y}(y | I) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} {\text{e}}^{\alpha y + \alpha \log_e \beta} {\text{e}}^{-{\text{e}}^{y + \log_e \beta}/\beta} $$

(82)

$$f_{y}(y | I) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} {\text{e}}^{\alpha y} {\text{e}}^{\alpha \log_e \beta} {\text{e}}^{-{\text{e}}^{y} {\text{e}}^{\log_e \beta}/\beta} $$

(83)

$$f_{y}(y | I) = \frac{1}{\beta^{\alpha} \Gamma (\alpha)} {\text{e}}^{\alpha y} \beta^{\alpha} {\text{e}}^{-{\text{e}}^{y} \beta/\beta} $$

(84)

$$f_{y}(y | I) = \frac{1}{\Gamma (\alpha)} {\text{e}}^{\alpha y} {\text{e}}^{-{\text{e}}^{y}}$$

(85)

Since the probability density function f _y (y|I) is independent of β, and identical to f _x (x|I) except shifted negatively by log _e β, the entropy of f _x (x|I) is also independent of β. This can be proved by expressing the expectation E(y) by the integral of the product of f _y (y|I) and y over the support set ${\mathcal{S}}_Y$ that is defined over the interval [−∞, ∞].

$$ E(y) = \int\limits_{{\mathcal{S}}_Y} f_{y}(y | I) y {\text{d}}y $$

(86)

$$ E(y) = \int\limits_{{\mathcal{S}}_Y} \frac{1}{\Gamma (\alpha)} {\text{e}}^{\alpha y} {\text{e}}^{-{\text{e}}^{y}} y {\text{d}}y $$

(87)

$$ E(y) = \frac{1}{\Gamma (\alpha)} \int\limits_{{\mathcal{S}}_Y} {\text{e}}^{\alpha y} {\text{e}}^{-{\text{e}}^{y}} y {\text{d}}y $$

(88)

Equation 66 can be expressed with respect to y where z = e^y and dz = e^ydy.

$$\frac{{\text{d}}}{{\text{d}}\alpha} \Gamma (\alpha) = \int\limits_{{\mathcal{S}}_Z} z^{\alpha - 1} {\text{e}}^{-z} \log_e z {\text{d}}z $$

(89)

$$\therefore \frac{{\text{d}}}{{\text{d}}\alpha} \Gamma (\alpha) = \int\limits_{{\mathcal{S}}_Y} {\text{e}}^{\alpha y} {\text{e}}^ {- {\text{e}}^y} y {\text{d}}y $$

(90)

Equation 90 expresses the integral term of Eq. 88 as the derivative of the gamma function. It can be divided by the gamma function to express the psi function Ψ (α) as defined in Eq. 69.

$$ E(y) = \frac{1}{\Gamma (\alpha)} \frac{{\text{d}} \Gamma (\alpha)}{{\text{d}} \alpha} = \Psi (\alpha) $$

(91)

Since x is y + log _e β, its expectation E(x) can be expressed with respect to E(y).

$$ E(x) = E(y) + \log_e \beta $$

(92)

$$ E(x) = \Psi (\alpha) + \log_e \beta $$

(93)

The expression for E(x) can thus be substituted into Eq. 79.

$$s[{\mathbf{x}}] = \alpha \log_e \beta + \log_e \Gamma (\alpha) - \alpha (\Psi (\alpha) + \log_e \beta) + \alpha $$

(94)

$$s[{\mathbf{x}}] = \alpha \log_e \beta + \log_e \Gamma (\alpha) - \alpha \Psi (\alpha) - \alpha \log_e \beta + \alpha $$

(95)

$$\therefore s[{\mathbf{x}}] = \log_e \Gamma (\alpha) - \alpha \Psi (\alpha) + \alpha $$

(96)

Approximation of the log interval entropy of a gamma process

If α is a positive integer, the gamma function Γ (α) can be expressed by factorial (a−1)!. Using Stirling’s formula (Harris and Stocker 1998), Γ (α+1) can be approximated for large values of α.

$$\Gamma (\alpha+1) = \alpha ! \approx \sqrt{2 \pi \alpha} \alpha^{\alpha} {\text{e}}^{-\alpha} $$

(97)

Since Γ (α+1) equals α Γ (α) (Press et al. 2002), it is possible to approximate log _e Γ (α).

$$ \log_e \Gamma (\alpha) \approx \log_e \left(\frac{1}{\alpha} \sqrt{2 \pi \alpha} \alpha^{\alpha} {\text{e}}^{-\alpha} \right) $$

(98)

$$ \log_e \Gamma (\alpha) \approx \log_e ( (2 \pi \alpha)^{\frac{1}{2}} \alpha^{\alpha-1} {\text{e}}^{-\alpha}) $$

(99)

$$ \log_e \Gamma (\alpha) \approx \frac{1}{2} \log_e ( 2 \pi \alpha) + (\alpha-1) \log_e \alpha -\alpha $$

(100)

$$ \log_e \Gamma (\alpha) \approx \frac{1}{2} \log_e ( 2 \pi) + \frac{1}{2} \log_e \alpha + \alpha \log_e \alpha - \log_e \alpha -\alpha $$

(101)

$$\therefore \log_e \Gamma (\alpha) \approx \frac{1}{2} \log_e (2 \pi) - \frac{1}{2} \log_e \alpha + \alpha \log_e \alpha -\alpha $$

(102)

The function Ψ (α) can be expressed with respect to Euler’s constant γ by summation.

$$\Psi (\alpha) = -\gamma + \sum\limits_{i=1}^{\alpha-1} \frac{1}{i} $$

(103)

where γ is Euler’s constant that can be expressed with respect to an infinite summation.

$$\gamma = {\mathop {\lim }\limits_{j \to \infty} } \left(- \log_e j + \frac{1}{1} + \frac{1}{2} + \cdots + \frac{1}{j} \right) $$

(104)

$$\gamma = {\mathop {\lim }\limits_{\delta w \to \infty} } \left(-\log_e j + \sum\limits_{i = 1}^{j} \frac{1}{i} \right) $$

(105)

Although the summation of reciprocals is divergent (Blakey 1949), the negative logarithmic term converges the value of the expression to a single quantity (≈ 0.5772). If α is large, it can be used to provide an approximation for γ.

$$\gamma \approx - \log_e \alpha + \sum\limits_{i = 1}^{\alpha}\frac{1}{i} $$

(106)

The approximation of γ can be substituted into Eq. 103.

$$ \Psi (\alpha) \approx \log_e \alpha - \sum\limits_{i = 1}^{\alpha} \frac{1}{i} + \sum\limits_{i=1}^{\alpha-1} \frac{1}{i} $$

(107)

$$ \Psi (\alpha) \approx \log_e \alpha - \left(\sum\limits_{i = 1}^{\alpha-1} \frac{1}{i} \right) - \frac{1}{\alpha} + \sum\limits_{i=1}^{\alpha-1} \frac{1}{i} $$

(108)

$$\therefore \Psi (\alpha) \approx \log_e \alpha - \frac{1}{\alpha} $$

(109)

Equations 102 and 109 can thus be used to approximate s[x] expressed in Eq. 28.

$$ s[{\mathbf{x}}] \approx \left(\frac{1}{2} \log_e (2 \pi) - \frac{1}{2} + \log_e \alpha + \alpha \log_e \alpha -\alpha \right) - \alpha \left(\log_e \alpha - \frac{1}{\alpha}\right) + \alpha $$

(110)

$$ s[{\mathbf{x}}] \approx \frac{1}{2} \log_e (2 \pi) - \frac{1}{2} \log_e \alpha + \alpha \log_e \alpha - \alpha - \alpha \log_e \alpha + \alpha \frac{1}{\alpha} + \alpha $$

(111)

$$ s[{\mathbf{x}}] \approx \frac{1}{2} \log_e (2 \pi) - \frac{1}{2} \log_e \alpha + 1 $$

(112)

$$ s[{\mathbf{x}}] \approx \frac{1}{2} \log_e \left(\frac{2 \pi}{\alpha} \right) + \log_e e $$

(113)

$$\therefore s[{\bf x}] \approx \frac{1}{2} \log_e \left(\frac{2 \pi e}{\alpha}\right) $$

(114)