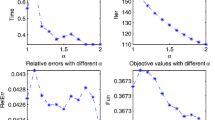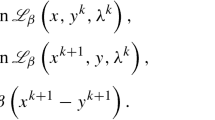Skip to main content
SpringerLink
Log in

Alternating direction method of multipliers with difference of convex functions

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

In this paper, we consider the minimization of a class of nonconvex composite functions with difference of convex structure under linear constraints. While this kind of problems in theory can be solved by the celebrated alternating direction method of multipliers (ADMM), a direct application of ADMM often leads to difficult nonconvex subproblems. To address this issue, we propose to convexify the subproblems through a linearization technique as done in the difference of convex functions algorithm (DCA). By assuming the Kurdyka-Łojasiewicz property, we prove that the resulting algorithm sequentially converges to a critical point. It turns out that in the applications of signal and image processing such as compressed sensing and image denoising, the proposed algorithm usually enjoys closed-form solutions of the subproblems and thus can be very efficient. We provide numerical experiments to demonstrate the effectiveness of our algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Boley, D.: Local linear convergence of the alternating direction method of multipliers on quadratic or linear programs. SIAM J. Optim. 23(4), 2183–2207 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bolte, J., Daniilidis, A., Lewis, A.: The łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17(4), 1205–1223 (2007)

    Article  MATH  Google Scholar 

  3. Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Programm. 146(1-2), 459–494 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bregma, L.M.: The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7(3), 200–217 (1967)

    Article  MathSciNet  Google Scholar 

  5. Chen, G., Teboulle, M.: A proximal-based decomposition method for convex minimization problems. Math. Programm. 64(1), 81–101 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  6. Deng, W., Lai, M.-J., Peng, Z., Yin, W.: Parallel multi-block admm with o (1/k) convergence. Journal of Scientific Computing (2014)

  7. Deng, W., Yin, W.: On the global and linear convergence of the generalized alternating direction method of multipliers. Journal of Scientific Computing, pp. 1–28 (2016)

  8. Eckstein, J., Yao, W.: Understanding the convergence of the alternating direction method of multipliers Theoretical and computational perspectives. Pacific Journal of Optimization (2015)

  9. Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput. Math. Appl. 2(1), 17–40 (1976)

    Article  MATH  Google Scholar 

  10. Gasso, G., Rakotomamonjy, A., Canu, S.: Recovering sparse signals with a certain family of nonconvex penalties and dc programming. IEEE Trans. Signal Process. 57(12), 4686–4698 (2009)

    Article  MathSciNet  Google Scholar 

  11. Glowinski, R., Marroco, A.: Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de dirichlet non linéaires. Rev. Fr. d’automatique, Inf., Rech. Opérationnelle Anal. Numérique 9(R2), 41–76 (1975)

    MATH  Google Scholar 

  12. Goldstein, T., Osher, S.: The split bregman method for l1-regularized problems. SIAM J. Imaging Sci. 2(2), 323–343 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. He, B., Yuan, X.: On non-ergodic convergence rate of douglas–rachford alternating direction method of multipliers. Numer. Math. 130(3), 567–577 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. He, B., Yuan, X.: On the o(1/n) convergence rate of the douglas-rachford alternating direction method. SIAM J. Numer. Anal. 50(2), 700–709 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Hong, M., Luo, Z.-Q.: On the linear convergence of the alternating direction method of multipliers. arXiv preprint arXiv:1208.3922 (2012)

  16. Kurdykam, K.: On gradients of functions definable in o-minimal structures. In: Annales de l’institut Fourier, vol. 48, pp. 769–784. L’Institut, 1950-, Chartres (1998)

  17. Li, G., Pong, T.K.: Splitting methods for nonconvex composite optimization. arXiv preprint arXiv:1407.0753 (2014)

  18. Lin, Z., Liu, R., Su, Z.: Linearized alternating direction method with adaptive penalty for low-rank representation. In: Advances in Neural Information Processing Systems, pp. 612–620 (2011)

  19. Łojasiewicz, S.: Sur la géométrie semi-et sous-analytique. Ann. Inst. Fourier 43(5), 1575–1595 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  20. Lou, Y., Yin, P., He, Q., Xin, J.: Computing sparse representation in a highly coherent dictionary based on difference of l 1 and l 2. J. Sci. Comput. 64(1), 178–196 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Lou, Y., Yin, P., Xin, J.: Point source super-resolution via non-convex l 1 based methods. J. Sci. Comput. 68(3), 1082–1100 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  22. Lou, Y., Zeng, T., Osher, S., Xin, J.: A weighted difference of anisotropic and isotropic total variation model for image processing. SIAM J. Imaging Sci. 8(3), 1798–1823 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mordukhovich, Boris S: Variational analysis and generalized differentiation I: Basic theory, vol. 330. Springer Science & Business Media (2006)

  24. Ng, M.K., Weiss, P., Yuan, X.: Solving constrained total-variation image restoration and reconstruction problems via alternating direction methods. SIAM J. Sci. Comput. 32(5), 2710–2736 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Osher, S., Burger, M., Goldfarb, D., Xu, J., Yin, W.: An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 4(2), 460–489 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  26. Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1(3), 123–231 (2013)

    Google Scholar 

  27. Tyrrell Rockafellar, R., Wets, R.J.-B.: Variational Analysis, vol. 317. Springer Science & Business Media (2009)

  28. Rockafellar, R.T.: Convex Analysis. Princeton University Press, USA (2015)

    MATH  Google Scholar 

  29. Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Phys. D: Nonlinear Phenom. 60(1), 259–268 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  30. Wang, F., Xu, Z., Xu, H.-K.: Convergence of alternating direction method with multipliers for non-convex composite problems. arXiv:1410.8625 (2014)

  31. Wang, H., Banerjee, A.: Bregman alternating direction method of multipliers. In: Advances in Neural Information Processing Systems, pp. 2816–2824 (2014)

  32. Wang, X., Yuan, X.: The linearized alternating direction method of multipliers for dantzig selector. SIAM J. Sci. Comput. 34(5), A2792–A2811 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 1(3), 248–272 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  34. Yu, W., Yin, W., Zeng, J.: Global convergence of admm in nonconvex nonsmooth optimization. arXiv:1511.06324 (2015)

  35. Wen, Z., Goldfarb, D., Yin, W.: Alternating direction augmented lagrangian methods for semidefinite programming. Math. Programm. Comput. 2(3-4), 203–230 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Xu, Y., Yin, W., Wen, Z., Zhang, Y.: An alternating direction algorithm for matrix completion with nonnegative factors. Frontiers Math. China 7(2), 365–384 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  37. Yang, J., Zhang, Y.: Alternating direction algorithms for l1-problems in compressive sensing. Siamj. Sci. Comput. 33, 250278 (2011)

    Google Scholar 

  38. Yang, J., Zhang, Y., Yin, W.: A fast alternating direction method for tvl1-l2 signal reconstruction from partial fourier data. IEEE J. Select. Top. Signal Process. 4(2), 288–297 (2010)

    Article  Google Scholar 

  39. Yin, P., Lou, Y.i, He, Q., Xin, J.: Minimization of 1-2 for compressed sensing. SIAM J. Sci. Comput. 37(1), A536–A563 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  40. Yin, P., Xin, J.: Iterative l 1 minimization for non-convex compressed sensing. Journal of Computational Mathematics, to appear

  41. Yin, W.: Analysis and generalizations of the linearized bregman method. SIAM J. Imaging Sci. 3(4), 856–877 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  42. Yin, W., Osher, S., Goldfarb, D., Darbon, J.: Bregman iterative algorithms for ℓ 1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 1(1), 143–168 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors are thankful to the editors and anonymous referees for their useful suggestions. T. Sun, L. Chen, and H. Jiang are grateful for the support from the National Science Foundation of China (No.61402495).

Author information

Authors and Affiliations

  1. College of Science, National University of Defense Technology, Changsha, Hunan, 410073, People’s Republic of China

    Tao Sun

  2. Department of Mathematics, University of California, Los Angeles, CA, 90095, USA

    Penghang Yin

  3. College of Science & The State Key Laboratory for High Performance Computation, National University of Defense Technology, Changsha, Hunan, 410073, People’s Republic of China

    Lizhi Cheng

  4. College of Computer, National University of Defense Technology, Changsha, Hunan, 410073, People’s Republic of China

    Hao Jiang

Authors
  1. Tao Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Penghang Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lizhi Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hao Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tao Sun.

Additional information

Communicated by: Stephen Wright

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, T., Yin, P., Cheng, L. et al. Alternating direction method of multipliers with difference of convex functions. Adv Comput Math 44, 723–744 (2018). https://doi.org/10.1007/s10444-017-9559-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10444-017-9559-3

Keywords

Mathematics Subject Classification (2010)

Search

Navigation