Abstract
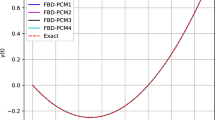
We prove the wellposedness of a nonlinear variable-order fractional differential equation and the regularity of its solutions. The regularity of the solutions is determined solely by the values of the variable order and its high-order derivatives at time t = 0 (in addition to the usual regularity assumptions on the variable order and the coefficients). If the variable-order reduces to an integer order at t = 0, then the solution has full regularity as the solution to a first-order ordinary differential equation. In this case, we prove that the corresponding finite difference scheme discretized on a uniform mesh has an optimal-order convergence rate. However, if the variable order does not reduce to an integer order at t = 0, then the solution has a singularity at time t = 0, as Stynes et al. proved in [15] for the constant-order time-fractional diffusion equations. The corresponding finite difference scheme discretized on a uniform mesh has only a suboptimal-order convergence rate. Instead, we prove that the finite difference scheme discretized on a graded mesh determined by the value of the variable order at time t = 0 has an optimal-order convergence rate in terms of the number of the time steps. Numerical experiments substantiate these theoretical results.
Similar content being viewed by others
References
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces. Elsevier, San Diego (2003)
Applebaum, D.: Lévy Processes and Stochastic Calculus. Cambridge University Press, United Kingdom (2009)
Diethelm, K.: The analysis of fractional differential equations, ser. Lecture notes in mathematics, vol. 2004. Springer, Berlin (2010)
Diethelm, K.: On the asymptotic behavior of solutions to fractional order differential equations, International Conference on Modeling, Analysis, and Numerics for Nonlocal Applications, Santa Fe, New Mexico (2017)
Diethelm, K., Ford, N.: A note on the well-posedness of terminal value problems for fractional differential equations. J. Integral Eqn. Appl., in press
Fu, H., Ng, M.K., Wang, H.: A divide-and-conquer fast finite difference method for space–time fractional partial differential equation. Comput. Math. Appl. 73, 1233–1242 (2017)
Jiang, S., Zhang, J., Zhang, Q., Zhang, Z.: Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 21, 650–678 (2017)
Ke, R., Ng, M.K., Sun, H. -W.: A fast direct method for block triangular Toeplitz-like with tri-diagonal block systems from time-fractional partial differential equations. J. Comput. Phys. 303, 203–211 (2015)
Kilbas, A., Srivastava, H., Trujillo, J.: Theory and applications of fractional differential equations, vol. 204. Elsevier, New York (2006)
Li, Z., Wang, H., Xiao, R., Yang, S.: A variable order fractional differential equation model of shape memory polymers, Chaos. Solitons Fractals 102, 473–485 (2017)
Lorenzo, C.F., Hartley, T.T.: Variable order and distributed order fractional operators. Nonlinear Dyn. 29, 57–98 (2002)
Meerschaert, M.M., Sikorskii, A.: Stochastic Models for Fractional Calculus, De Gruyter Studies in Mathematics (2011)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)
Shao, J.: New integral inequalities with weakly singular kernel for discontinuous functions and their applications to impulsive fractional differential systems. J. Appl. Math. 2014, 1–5 (2014)
Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded mesh for a time-fractional diffusion equation. SIAM Numer. Anal. 55, 1057–1079 (2017)
Sun, H., Chen, W., Chen, Y.: Variable-order fractional differential operators in anomalous diffusion modeling. Physica A: Stat. Mech. Appl. 388, 4586–4592 (2009)
Sun, H., Chen, W., Wei, H., Chen, Y.: A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 193, 185–192 (2011)
Umarov, S.R., Steinberg, S.T.: Variable order differential equations with piecewise constant order-function and diffusion with changing modes. ZAA 28, 131–150 (2009)
Wu, X., Deng, W., Barkai, E.: Tempered fractional Feynman-Kac equation: theory and examples. Physical Rev. Lett. 93, 032151 (2016)
Zeng, F., Zhang, Z., Karniadakis, G.: A generalized spectral collocation method with tunable accuracy for variable-order fractional differential equations. SIAM Sci. Comp. 37, A2710–A2732 (2015)
Zhuang, P., Liu, F., Anh, V., Turner, I.: Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term. SIAM Numer. Anal. 47, 1760–1781 (2009)
Acknowledgments
The authors would like to express their most sincere thanks to the referees for their very helpful comments and suggestions, which greatly improved the quality of this paper.
Funding
This work was funded by the OSD/ARO under MURI Grant W911NF-15-1-0562 and the National Science Foundation under Grant DMS-1620194.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: Martin Stynes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wang, H., Zheng, X. Analysis and numerical solution of a nonlinear variable-order fractional differential equation. Adv Comput Math 45, 2647–2675 (2019). https://doi.org/10.1007/s10444-019-09690-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10444-019-09690-0