Ambient residual penalty approximation of partial differential equations on embedded submanifolds

Abstract

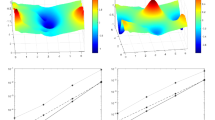
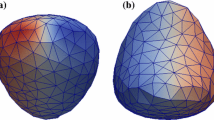
In this paper, we present a novel approach to the approximate solution of elliptic partial differential equations on compact submanifolds of $\mathbb {R}^{d}$, particularly compact surfaces and the surface equation ${\Delta }_{\mathbb {M}} u - \lambda u=f$. In the course of this, we reconsider differential operators on such submanifolds to deduce suitable penalty based functionals. These functionals are based on the residual of the equation in an integral representation, extended by a penalty on the first-order normal derivative. The general framework we develop is accompanied by error analysis and exemplified by numerical examples employing tensor product B-splines.

Appendix

1.1 A.1 Parameterising compact submanifolds

For technical reasons it is convenient to give some of the arguments in the following proofs using an inverse atlas for the submanifold. Therefore, we will briefly recall a suitable inverse atlas, using [34, Sect. 9.1] and almost copying the corresponding statements in [35, Sect. 6]:

As our submanifolds are required to be compact, we can assume to be equipped with some finite inverse atlas $\{(\varphi _{i},{\omega ^{0}_{i}})\}_{i\in I}$ where each ${\omega ^{0}_{i}}\subseteq {\mathbb R}^{k}$ is a ball of fixed radius δ₀ > 0. On each of these balls, φ_i is a so-called exponential map$\exp _{\xi _{i},{\mathbb M}}$ of ${\mathbb M}$ around $\xi _{i}\in {\mathbb M}$ with ξ_i = φ_i(0). For any arbitrary $\xi \in {\mathbb M}$, the exponential map is defined as

$$ \exp_{\xi,{\mathbb M}}(x):=\begin{cases} \xi&\textup{ if } x=0\\ \gamma_{\xi, x}(\| x\|_{2})&\textup{ otherwise} \end{cases}, $$

where γ_{ξ, x} is the uniquely defined arc-length parameterisation for the geodesic that contains ξ and has direction v_x for some suitable identification v_x in ${\mathrm T}_{\xi }{\mathbb M}$ of x in ${\mathbb R}^{k}$. The validity of this construction is a consequence of the compactness of ${\mathbb M}$ and the fact that the so-called injectivity radiusδ(y) in which the exponential map is an injective map to $\mathbb {M}$ is itself a smooth function of $y\in {\mathbb M}$ (cf. [5, Paragr. 3], [8, Prop. 88]). In particular, we can thereby determine a minimax injectivity radius $\delta _{{\mathbb M}}$ that is valid over all of ${\mathbb M}$.

Moreover, by the same arguments we can demand that δ₀ > 0 is chosen such that there are $\delta _{1}<\delta _{0}<\delta _{2}<\delta _{{\mathbb M}}$ and the balls with radii δ₁, δ₂ yield an inverse atlas as well. For future reference, we term those balls as parameter spaces by ${\omega ^{1}_{i}}{\subset \omega ^{0}_{i}}{\subset \omega ^{2}_{i}}$.

Furthermore, suitably shrinking δ₁, δ₀, δ₂ further if necessary, we can also demand that there are smooth maps T_i and N_i that assign orthonormal frames of the tangent and normal space in $\varphi _{i}(x)\in {\mathbb M}$ to $x{\in \omega _{i}^{j}}$, respectively, for j = 0, 1, 2.

By another compactness argument, we can then deduce that all three maps φ_i, T_i, N_i are C-bounded on the balls of radius δ₂. That is, for any multi-index α and all i ∈ I there is a constant c_α > 0 such that it holds |D^αg(x)| < c_α for g = φ_i, T_i, N_i and any $x{\in \omega _{i}^{2}}$ (cf. [32]).

1.2 A.2 Proof of Lemma 2

First of all, we recall right from above that there is a locally smooth map $N:\varphi (\omega )\subseteq {\mathbb M}\to {\mathbb R}^{d\times (d-k)}$ that assigns an orthonormal frame ν¹(y), ... , ν^d−k(y) of the normal space ${\mathrm N}_{y}{\mathbb M}$ to each y ∈ φ(ω). We conclude immediately by the definition of the tangential Hessian that locally for any $v,w\in {\mathrm T}{\mathbb M}$

$$ H_{f,{\mathbb M}}(v,w)=v^{t} H_{F}w-v^{t} D\left( N\cdot\nabla_{{\mathrm N}} F\right) w. $$

Looking closer at the remaining D(N ⋅∇_NF), we find by the product rule

$$ D(N\cdot\nabla_{{\mathrm N}} F) =\sum\limits_{i=1}^{d-k}\nu^{i}\cdot D\left( \mathrm D_{\nu^{i}}F\right) +\sum\limits_{i=1}^{d-k}\left( \mathrm D_{\nu^{i}}F\right){\kern1.7pt}(D\nu^{i}). $$

Multiplication of this by cotangent v^t from the left and by tangent w from the right will annihilate the first sum. This in mind, we can reinsert and obtain

$$ H_{f,{\mathbb M}}(x)(v,w)=v^{t} H_{f}(x)w-v^{t}\left( \sum\limits_{i=1}^{d-k}\left( \mathrm D_{\nu^{i}}F\right)(x){\kern1.7pt}(D\nu^{i})(x)\right) w. $$

As the bilinear form induced by Dνⁱ(x) can be assumed to be bounded for any i = 1, ... , d − k, because N can be chosen to be C-bounded, we directly deduce that

$$ \begin{array}{@{}rcl@{}} \left| v^{t} D\left( N\cdot\frac{\partial F}{\partial_{{\mathrm N}}}\right) w\right| &\le& \max\limits_{1\le i\le d-q}\left|\mathrm D_{\nu^{i}}F(x)\right|\cdot \sum\limits_{i=1}^{d-k}\left| v^{t} D\nu^{i}(x) w \right| \\ &\le& c \max\limits_{\nu\in {\mathrm N}_{x}{\mathbb M}\atop \|\nu\|_{2}=1}|\mathrm D_{\nu} F(x)| \cdot\|v\|_{2}\cdot\|w\|_{2}. \end{array} $$

Hence, we obtain the desired result.

1.3 A.3 Proof of ${\mathrm H}^{1}({\mathbb M})={\mathrm H}^{1}_{\textsc {t}}({\mathbb M}),{\mathrm H}^{2}({\mathbb M})={\mathrm H}^{2}_{\textsc {t}}({\mathbb M})$

Since we have a finite inverse atlas, we restrict ourselves here to one pair (φ, ω) from the inverse atlas, and we understand the norms $\left |\!\!{}\left | f\right |\!\!{}\right |_{{\mathrm H}_{\textsc {t}}^{1}({\mathbb M})}$ and $\left |\!\!{}\left | f\right |\!\!{}\right |_{{\mathrm H}_{\textsc {t}}^{2}({\mathbb M})}$ in the Sobolev case as metric closures of the smooth functions. Then by the transformation law

$$ c_{1}\left|\!\!{\kern2.2pt}\left| f\circ\varphi\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}(\omega)}^{2}\le\int\limits_{\varphi(\omega)} |f|^{2}\le c_{2}\left|\!\!{\kern2.2pt}\left| f\circ\varphi\right|\!\!{\kern2.2pt}\right|_{\mathrm{L}_{2}(\omega)}^{2}. $$

By considering additionally the chain rule and the fact that the jacobian J_φ(x) maps $x\in {\mathbb M}$ onto a basis frame for the tangent space, and this map is C-bounded, we can further deduce that

$$ c_{1}\int\limits_{\omega} |\nabla (f\circ\varphi)|^{2}\le\int\limits_{\varphi(\omega)} |\nabla_{{\mathbb M}} f|^{2}\le c_{2}\int\limits_{\omega} |\nabla (f\circ\varphi)|^{2}. $$

So we need to take care about the second-order terms only. Recalling the notation ${\mathrm {E\!\!{}x}}_{{\mathrm N}} f$, we have for arbitrary coordinate directions x_i, x_j with respect to ω that by the chain rule

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{2} ({{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\circ\varphi)}{\partial x_{i} \partial x_{j}}&=& \left( \frac{\partial\varphi_{1}}{\partial x_{i}}, ... , \frac{\partial\varphi_{d}}{\partial x_{i}}\right)\cdot H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f}(\varphi(x)) \cdot\left( \frac{\partial\varphi_{1}}{\partial x_{j}}, ... , \frac{\partial\varphi_{d}}{\partial x_{j}}\right)^{t}\\ &&+ {\sum}_{\ell=1}^{d} \partial_{\ell} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f \frac{\partial^{2}\varphi_{\ell}}{\partial x_{i}\partial x_{j}}. \end{array} $$

By definition, the set

$$ \left\{\partial_{i}\varphi:=\left( \frac{\partial\varphi_{1}}{\partial x_{i}}, ... , \frac{\partial\varphi_{d}}{\partial x_{i}}\right)^{t}\right\}_{i=1}^{k} $$

forms a pointwise basis of the tangent space, and the corresponding basis transform has a bounded spectrum due to C-boundedness by conception of the inverse atlas. So we can deduce by standard linear algebra arguments on basis changes that for bases τ¹, ... , τ^k (making up the frame Tⁱ(x)) and ∂₁φ, ... , ∂_kφ of $\mathrm {T}_{x}(\mathbb {M})$

$$ \begin{array}{@{}rcl@{}} \left( \frac{\partial^{2} ({{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\circ\varphi)}{\partial x_{i} \partial x_{j}}\right)^{2} &\le&\left( \left|(\partial_{i}\varphi)^{t}\cdot H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f}(\varphi(x))\cdot(\partial_{j}\varphi)\right| + \left|{\sum}_{\ell=1}^{d} \partial_{\ell} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\frac{\partial^{2}\varphi_{\ell}}{\partial x_{i}\partial x_{j}}\right|\right)^{2}\\ &\le& c \left|(\partial_{i}\varphi)^{t}\cdot H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f}(\varphi(x))\cdot(\partial_{j}\varphi)\right|^{2} \!\!\!+ c \left|{\sum}_{\ell=1}^{d} \partial_{\ell} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f \frac{\partial^{2}\varphi_{\ell}}{\partial x_{i}\partial x_{j}}\right|^{2}\\ &\le& c {\sum}_{i,j=1}^{k}H_{f,{\mathbb M}}(\tau^{i},\tau^{j})^{2}+ c \left\langle \nabla_{{\mathbb M}} f,\nabla_{{\mathbb M}} f\right\rangle^{2}, \end{array} $$

where we used further that $\nabla _{{\mathbb M}} f=\nabla {{\mathrm {E\!\!{}x}}_{\mathrm N}} f$ by conception. Thereby, we can deduce in turn that

$$ \int\limits_{\omega} {\sum}_{i,j=1}^{k}\left( \frac{\partial^{2} ({{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\circ\varphi)}{\partial x_{i} \partial x_{j}}\right)^{2}\le c\left|\!\!{\kern2.2pt}\left| f\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}_{\textsc{t}}^{2}({\mathbb M})}^{2}, $$

which gives one part of the required inequality. For the other, we argue by contradiction: We assume that we have a sequence $(f_{n})_{n\in \mathbb {N}}$ of functions with corresponding $\mathrm {E\!\!{}x}_{\mathrm {N}} f_{n}=\mathrm {E\!\!{}x}_{\mathrm {N}} f_{n}$ such that $\left |\!\!{}\left | f_{n}\right |\!\!{}\right |_{{\mathrm H}_{\textsc {t}}^{2}({\mathbb M})}^{2}\ge 1$ but

$$ \left|\!\!{\kern2.2pt}\left| f_{n}\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{2}({\mathbb M})}<\frac{1}{n}\quad\forall n\in{\mathbb N}. $$

Without restriction, we demand these functions to be smooth. Then, we can directly deduce from the known equivalence of $\left |\!\!{}\left | f\right |\!\!{}\right |_{\mathrm {H}^{1}(\mathbb {M})}$ and $\left |\!\!{}\left | f\right |\!\!{}\right |_{\mathrm {H}^{1}_{\textsc {t}}(\mathbb {M})}$, and from Sobolev embeddings, that also

$$ \left|\!\!{\kern2.2pt}\left| f_{n}\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{1}_{\textsc{t}}({\mathbb M})}< c\frac{1}{n}, $$

so again it boils down to the second-order term only. There we see now that in particular

$$ \int\limits_{\omega} \left( \frac{\partial^{2} ({{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}\circ\varphi)}{\partial x_{i} \partial x_{j}}\right)^{2} <\frac{1}{n}. $$

(A.3.1)

On the other hand, we can deduce with $\partial _{i,j}\varphi := \left (\frac {\partial ^{2}\varphi _{1}}{\partial x_{i}\partial x_{j}}, ... , \frac {\partial ^{2}\varphi _{d}}{\partial x_{i}\partial x_{j}}\right )^{t}$ and the chain rule

$$ \begin{array}{@{}rcl@{}} \left( \frac{\partial^{2} ({{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}\circ\varphi)}{\partial x_{i} \partial x_{j}}\right)^{2} &=& \left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)+\left\langle \partial_{i,j}\varphi,\nabla_{{\mathbb M}} f_{n}\right\rangle\right)^{2}\\ &\ge& \left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)^{2}\\ &&- 2\left|\left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)\cdot\left\langle \partial_{i,j}\varphi,\nabla_{{\mathbb M}} f_{n}\right\rangle\right|. \end{array} $$

Integrating over both after summing over all i, j gives

$$ \frac{1}{n}> \int\limits_{\omega}\sum\limits_{i,j=1}^{k}\left( \frac{\partial^{2} ({{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}\circ\varphi)}{\partial x_{i} \partial x_{j}}\right)^{2} $$

$$ \begin{array}{@{}rcl@{}} &\ge& \int\limits_{\omega}\sum\limits_{i,j=1}^{k}\left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)^{2}{\kern1.7pt}d\omega\\ &&-2\int\limits_{\omega}\sum\limits_{i,j=1}^{d}\left|\left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)\cdot\left\langle \partial_{i,j}\varphi,\nabla_{{\mathbb M}} f_{n}\right\rangle\right|{\kern1.7pt}d\omega. \end{array} $$

(A.3.2)

On the other hand, Hölder’s inequality and (A.3.1) gives that

$$ \begin{array}{@{}rcl@{}} &&{\sum}_{i,j=1}^{k}\int\limits_{\omega}\left|\left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)\cdot\left\langle \partial_{i,j}\varphi,\nabla_{{\mathbb M}} f_{n}\right\rangle\right|\\ \!\!&\le&\!\! c {\sum}_{i,j=1}^{k}\left( \int\limits_{\omega} \left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)^{2} \right)^{\frac{1}{2}}\!\cdot\!\left( \int\limits_{\omega} \left\langle \partial_{i,j}\varphi,\partial_{i,j}\varphi\right\rangle\left\langle \nabla_{{\mathbb M}} f_{n},\nabla_{{\mathbb M}} f_{n}\right\rangle \right)^{\frac{1}{2}}\\ \!\!&\le&\!\! c \left|\!\!{\kern2.2pt}\left| f_{n}\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{2}}\left|\!\!{\kern2.2pt}\left| f_{n}\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{1}}\le c\cdot\frac{1}{n}. \end{array} $$

Inserting this in (A.3.2) and rearranging terms gives that

$$ \int\limits_{\omega}{\sum}_{i,j=1}^{k}\left( (\partial_{i}\varphi)^{t}H_{{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f_{n}}(\varphi(x))(\partial_{j}\varphi)\right)^{2}\le c\cdot\frac{1}{n}, $$

whereby we have deduced a contradiction.

1.4 A.4 Proving spline approximation of normal derivatives

1.4.1 A.4.1 Extended parameter spaces and parameterisations

With the assertions of Appendix A.1, we can use the inverse atlas for ${\mathbb M}$ to deduce a set of corresponding parameterisations {Φ_i}_i∈I and parameter spaces $\{{{\Omega }_{i}^{h}}\}_{i\in I}$ that parameterise $\mathbb {U}_{h}({\mathbb M})$ in a very convenient way: We choose ${{\Omega }_{i}^{h}}:=\omega _{i}\times {\mathrm B}^{(d-k)}_{h}(0)$ for open ball ${\mathrm B}^{(d-k)}_{h}(0)\subseteq {\mathbb R}^{(d-k)}$ of radius h and ν^j the j th basis vector of the normal frame according to N_i by

$$ {\Phi}_{i}:{{\Omega}_{i}^{h}}\to\mathbb{U}_{h}({\mathbb M}),\qquad{\Phi}_{i}(x,z) = \varphi_{i}(x)+{\sum}_{j=1}^{(d-k)} z_{j} \nu^{j}(x). $$

(A.4.1)

Moreover, we can in particular deduce the following lemma according to [35, Lem. 6.1], [34, Sect. 2.2], [36, Lem. 3]:

Lemma 6

Let$m\in {\mathbb N}$, let${\mathbb M}\subseteq {\mathbb R}^{d}$be a smooth compact submanifold, contained in a family$\mathbb {U}_{h}({\mathbb M})$of tubular neighbourhoods with 0 < h < h₀. Let (φ_i, ω_i)_i∈Iand$({\Phi }_{i},{{\Omega }_{i}^{h}})_{i\in I}$be the inverse atlases as introduced above. Then there are fixed a₁, a₂ > 0 independent of h such that for any$f\in {\mathrm H}^{m}({\mathbb M})$and fixed b₁, b₂ > 0 independent of h

$$ a_{1} h^{{(d-k)}/2} \|f\circ\varphi_{i}\|_{{\mathrm H}^{m}(\omega_{i})}\le \|\mathrm{E\!\!{\kern2.8pt}x}_{\mathrm{N}}f\|_{\mathrm{H}^{m}({\Phi}_{i}({{\Omega}_{i}^{h}}))}\le a_{2} h^{{(d-k)}/2}\|f\circ\varphi_{i}\|_{\mathrm{H}^{m}(\omega_{i})}, $$

whereby in particular for suitable c₁, c₂ > 0

$$ c_{1} h^{{(d-k)}/2} \|f\|_{{\mathrm H}^{m}({\mathbb M})}\le \|{\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}}f\|_{{\mathrm H}^{m}(\mathbb{U}_{h}({\mathbb M}))}\le c_{2} h^{{(d-k)}/2}\|f\|_{{\mathrm H}^{m}({\mathbb M})}. $$

1.4.2 A.4.2 The integer order case in Theorem 3

We will first concentrate on the integer order case, and deduce the fractional afterwards via some function space interpolation arguments. The proofs are quite similar to those provided in [35] for the standard norm approximation. We can reuse much of the lemmas and argumentation from there, with just a couple of suitable adaptions.

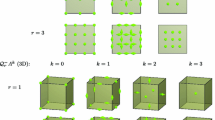
First of all, we recall a spline quasi-interpolation operator Q_h can be chosen such that it meets all the requirements presented in [32, 34, 35]. Revising this, we start with the set $\{B_{i,h}^{m}\}_{i\in {\mathbb Z}^{d}}$ of tensor product B-splines of order $m\in {\mathbb N}$ over the uniform grid $h{\mathbb Z}^{d}$, Then we choose a set of corresponding functionals $\{{\Lambda }_{i,h}\}_{i\in {\mathbb Z}^{d}}$ bounded on ${\mathrm L}_{2}({\mathbb R}^{d})$ such that Λ_{i, h}g = 0 for any g with support in the complement of the open ball ${\mathrm B}_{mdh}(ih):=\{x:\left |\!\!{}\left | x-ih\right |\!\!{}\right |_{2}<mdh\}$ and define

$$ {\mathrm Q}_{h} f = {\sum}_{i\in {\mathbb Z}^{d}} ({\Lambda}_{i,h}f) B_{i,h}^{m}. $$

For this kind of operator, the following lemma holds (cf. [35, Lem. 6.4/6.8], [34, Lem. 3.17/3.28]):

Lemma 7

Let $0<n \le m\in {\mathbb N}$ and 0 ≤ μ < n. Let B_h[ζ] := ζ + (−h, h)^d be the box centred at $\zeta \in {\mathbb R}^{d}$. Let ${{\mathrm S}_{h}^{m}}({\mathbb R}^{d})$ be the tensor product spline space of order m with grid width h. Then there is a spline quasi-interpolation operator Q_h such that for a constant c independent of h or $f\in {\mathrm H}^{n}({\mathrm B}_{bh}[\zeta ])$ and some b ≥ a ≥ 1

$$ \| f- p_{\zeta,f}\|_{{\mathrm H}^{\mu}({\mathrm B}_{ah}[\zeta])} \le c h^{n -\mu} \| f\|_{{\mathrm H}^{n }({\mathrm B}_{bh}[\zeta])}, $$

where p_{ζ, f} is the polynomial that coincides with Q_hf on one spline cell that contains ζ.

This operator is subsequently applied to ${\mathrm {E\!\!{}x}}_{{\mathrm N}} f$ in order to accomplish the desired proof of Theorem 3. To this end, we let $\{{\textsc c}_{h}(\zeta )\}_{\zeta \in {\mathrm {Z}_{a,h}}}$ be the set of cells of length h that belong to basis functions whose support intersects $\mathbb {U}_{h}({\mathbb M})$. Let therein the set Z_{a, h} contain the centres of these cells, so that again each cell has the form ζ + (−h/2, h/2)^d.

Let then $S_{h} ={\mathrm Q}_{h} {\mathrm {E\!\!{}x}}_{{\mathrm N}} f$ on these cells and let s_h be its trace on ${\mathbb M}$. Let c_h be an arbitrary cell. Then $(S_{h})_{|{\textsc c}_{h}}=P_{{\textsc c}_{h}}$ for some polynomial $P_{{\textsc c}_{h}}$ of order m, and we call by $p_{{\textsc c}_{h}}={\mathrm {T\!\!{}r}}_{{\mathbb M}} P_{{\textsc c}_{h}}$ the trace of $P_{{\textsc c}_{h}}$, seen as a polynomial on ${\mathbb R}^{d}$, on all of ${\mathbb M}$. Because any cell is compactly contained in the respective box B_h[ζ] := ζ + (−h, h)^d, we have that

$$ \begin{array}{@{}rcl@{}} \|\nabla_{{\mathrm N}} S_{h}\|_{{\mathrm L}_{2}({\mathbb M})}&\le c {\sum}_{\zeta\in{\mathrm{Z}_{a,h}}}\|\nabla_{{\mathrm N}} P_{{\textsc c}_{h}}\|_{{\mathrm L}_{2}({\mathbb M}\cap{\mathrm B}_{h}[\zeta])}. \end{array} $$

By [35, Sect. 3.2] and [34, Sect. 9.1.2] it is ensured that there is a suitable pair $({\Phi }_{i},{\Omega }_{i}^{ah}=\omega _{i}\times {\mathrm B}_{ah}^{(d-k)}(0))$ corresponding to some (φ_i, ω_i) from the inverse atlas and a suitable, globally valid a > 0 such that for $\xi ={\Phi }_{i}^{-1}(\zeta )$ it holds ${\Phi }_{i}^{-1}({\mathrm B}_{h}[\zeta ])\subseteq {\mathrm B}_{c_{1} h}[\xi ]\subset {\Omega }_{i}^{ah}$. With this choice, we proceed by omitting the index i ∈ I and the index c_h. To obtain the desired relation, we now have to look at the map N = (ν¹, ... , ν^(d−k)) that gives us a normal frame on the image of ω that is smooth and C-bounded on ω. We decompose then $\left |\!\!{}\left |(\nabla _{{\mathrm N}} P)\right |\!\!{}\right |_{2}^{2}$ as follows in a finite sum of normal directional derivatives: It holds in any φ(x) for x ∈ ω that

$$ \left|\!\!{\kern2.2pt}\left|\nabla_{{\mathrm N}} P\right|\!\!{\kern2.2pt}\right|_{2}^{2}={\sum}_{\ell=1}^{(d-k)} |\mathrm D_{\nu^{\ell}} P|^{2}\le c \left( {\sum}_{\ell=1}^{(d-k)} |\mathrm D_{\nu^{\ell}} P|\right)^{2}= c\left|\!\!{\kern2.2pt}\left|\nabla_{{\mathrm N}} P\right|\!\!{\kern2.2pt}\right|_{1}^{2}, $$

Consequently, we have with the triangle inequality, suitably increased c and ξ_ω as the orthogonal projection of ξ onto ω that

$$ \begin{array}{@{}rcl@{}} &\left|\!\!{\kern2.2pt}\left| (\nabla_{{\mathrm N}} P)\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}(\varphi(\omega)\cap{\mathrm B}_{h}[\zeta])} \le c{\sum}_{i=1}^{(d-k)} \left|\!\!{\kern2.2pt}\left| \left( \mathrm D_{\nu^{i}} P\right)\circ\varphi\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}(\omega\cap{\mathrm B}_{c_{2} h}[\xi_{\omega}])}. \end{array} $$

Now we have to notice that on each Ω we have by the definition of Φ via (A) and of N with its component column ν = ν^j that (D_νP) ∘Φ = ∂_j(P ∘Φ) for some standard coordinate direction j. We can thus obtain because of $\mathrm D_{\nu } {{\mathrm {E\!\!{}x}}_{\mathrm N}} f =0$ and Lemma 6 that

$$ \begin{array}{@{}rcl@{}} &&\left|\!\!{\kern2.2pt}\left| (\mathrm D_{\nu} P)\circ\varphi\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}(\omega\cap{\mathrm B}_{c_{2}h}[\xi_{\omega}])}\\ &\le& c h^{-\frac{{(d-k)}}{2}}\left|\!\!{\kern2.2pt}\left| {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}}(\mathrm D_{\nu} P)\circ{\Phi}\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}({\mathrm B}_{c_{2}h}[\xi_{\omega}])}\\ &=& c h^{-\frac{{(d-k)}}{2}}\left|\!\!{\kern2.2pt}\left| {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}}(\mathrm D_{\nu} P)\circ{\Phi}-(\mathrm D_{\nu} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f )\circ{\Phi}\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}({\mathrm B}_{c_{2}h}[\xi_{\omega}])}\\ &\le& c h^{-\frac{{(d-k)}}{2}}\left|\!\!{\kern2.2pt}\left| (\mathrm D_{\nu} P)\circ{\Phi}-(\mathrm D_{\nu} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f )\circ{\Phi}\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}({\mathrm B}_{c_{2}h}[\xi_{\omega}])}\\ &+& c h^{-\frac{{(d-k)}}{2}}\left|\!\!{\kern2.2pt}\left| (\mathrm D_{\nu} P)\circ{\Phi}-{\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}}(\mathrm D_{\nu} P)\circ{\Phi}\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}({\mathrm B}_{c_{2}h}[\xi_{\omega}])}. \end{array} $$

(A.4.2)

We invoke now the approximation order for tp-spline quasi-interpolation as presented in Lemma 7. The first summand can then be bounded by using the evident relation $|\mathrm D_{\nu } (P-{{\mathrm {E\!\!{}x}}_{\mathrm N}} f)|\le \left |\!\!{}\left | \nabla (P-{{\mathrm {E\!\!{}x}}_{\mathrm N}} f)\right |\!\!{}\right |_{2}$ in the form

$$ \left|\!\!{\kern2.2pt}\left| (\mathrm D_{\nu} (P-{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f))\circ{\Phi}\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}({\mathrm B}_{c_{2}h}[\xi_{\omega}])}\le\left|\!\!{\kern2.2pt}\left| (P-{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f)\circ{\Phi}\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{1}({\mathrm B}_{c_{2}h}[\xi_{\omega}])} $$

(A.4.3)

$$ \le c \left|\!\!{\kern2.2pt}\left| P-{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{1}({\mathrm B}_{ah}[\zeta])}\le h^{r-1}\left|\!\!{\kern2.2pt}\left| {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{r}({\mathrm B}_{bh}[\zeta])}. $$

Therein, b ≥ a > 0 are suitable fixed constants that can be chosen valid for any i ∈ I. For the second summand, we proceed via a version of Friedrichs’ inequality for arbitrary codimensions (cf. [35, Lem. 6.9] or [34, Thm. 9.24]) to obtain for $R := (\mathrm D_{\nu } P)\circ {\Phi }-({\mathrm {E\!\!{}x}}_{{\mathrm N}}(\mathrm D_{\nu } P))\circ {\Phi }$ the relation

$$ \begin{array}{@{}rcl@{}} \|R\|^{2}_{{\mathrm L}_{2}({\mathrm B}_{c_{2} h}[\xi_{\omega}])}\le c h^{2}{\sum}_{|\beta|=1}\|\partial_{z}^{\beta} R\|_{{\mathrm L}_{2}({\mathrm B}_{c_{2} h}[\xi_{\omega}])}^{2}. \end{array} $$

(A.4.4)

To achieve that, we notice that it holds $({\mathrm {E\!\!{}x}}_{{\mathrm N}}(\mathrm D_{\nu } P))({\Phi }(x,z))=({\mathrm {E\!\!{}x}}_{{\mathrm N}}(\mathrm D_{\nu } P))({\Phi }(x,0))$, whereby in particular $\partial _{z}^{\beta } (({\mathrm {E\!\!{}x}}_{{\mathrm N}}(\mathrm D_{\nu } P))\circ {\Phi })=0=\partial _{z}^{\beta }\partial _{j}({{\mathrm {E\!\!{}x}}_{\mathrm N}} f\circ {\Phi })$. Consequently we can deduce by virtue of Friedrichs’ inequality for functions that finite dimensional polynomials in certain coordinates [35, Lemma 6.9] that it holds

$$ \begin{array}{@{}rcl@{}} \|R\|^{2}_{{\mathrm L}_{2}({\mathrm B}_{c_{2} h}[\xi_{\omega}])}&\le c h^{2}{\sum}_{|\beta|=1}\|\partial_{z}^{\beta} \partial_{j}(P \circ{\Phi} - {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f \circ{\Phi})\|_{{\mathrm L}_{2}({\mathrm B}_{c_{2} h}[\xi_{\omega}])}^{2}\\ &\le c h^{2}{\sum}_{|\eta|=2}\|\partial_{z}^{\eta} (P \circ{\Phi} - {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f \circ{\Phi})\|_{{\mathrm L}_{2}({\mathrm B}_{c_{2} h}[\xi_{\omega}])}^{2}. \end{array} $$

Now we apply the approximation power of splines to (A.4.4), and deduce

$$ \left|\!\!{\kern2.2pt}\left| R\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}({\mathrm B}_{c_{2} h}[\xi_{\omega}])}\le c h \left|\!\!{\kern2.2pt}\left| P-{{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{2}({\mathrm B}_{ah}[\zeta])}\le h^{r-1}\left|\!\!{\kern2.2pt}\left| {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{r}({\mathrm B}_{bh}[\zeta])}. $$

(A.4.5)

Consequently, we can bound in (A.4.2) by (A.4.3) and (A.4.5) that

$$ \| \nabla_{{\mathrm N}} P\|_{{\mathrm L}_{2}({\mathrm B}_{h}[\zeta]\cap{\mathbb M})}\le c {h}^{r-1-{(d-k)}/2} \| {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}} f \|_{{\mathrm H}^{r}({\mathrm B}_{b h}[\zeta])}. $$

(A.4.6)

It remains to sum over all cells. To accomplish that, we have to choose b large enough to work out for each cell in at least one extended parameter space; this will be no problem if h₀ is small enough. And we have to choose h₀ small enough to achieve that $\mathbb {U}_{dbh}(\mathbb {M})$ has the closest point property. Then because b was fixed over a fixed extended parameter space and the number of these is finite, we can choose b maximal among them to become independent of the extended parameter spaces. Because clearly any $z\in \mathbb {U}_{dbh}(\mathbb {M})$ can be in at most n₀ balls B_bh[ζ] for some fixed n₀, we deduce

$$ {\sum}_{\zeta\in{\mathrm{Z}_{a,h}}}\| {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}} f \|_{{\mathrm H}^{r}({\mathrm B}_{b h}[\zeta])}\le c \| {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}} f \|_{{\mathrm H}^{r}(\mathbb{U}_{db h}({\mathbb M}))} $$

(A.4.7)

and obtain thereby with (A.4.6) and Lemma 6 that

$$ {\sum}_{\zeta\in{\mathrm{Z}_{a,h}}}\| \nabla_{{\mathrm N}} P\|_{{\mathrm L}_{2}({\mathrm B}_{h}[\zeta]\cap{\mathbb M})}\le c {h}^{r -1-{(d-k)}/2} \| {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}} f \|_{{\mathrm H}^{r}(\mathbb{U}_{db h}({\mathbb M}))}\le c {h}^{r -1}\| f \|_{{\mathrm H}^{r}({\mathbb M})}. $$

1.4.3 A.4.3 The fractional order case in Theorem 3

To deduce the fracional convergence orders for normal derivatives, we restrict ourselves now to an arbitrary $(\varphi _{i},{\omega _{i}^{0}})$ with corresponding $(\varphi _{i},{\omega _{i}^{2}})$. This is feasible, as all the orders provided for the integer case are valid there as well: The integer proof essentially just took place on one such parameter space. The only modification to make affects the cells considered: We would no longer use all cells that intersect ${\mathbb M}$, but only those that intersect $\varphi ({\omega _{i}^{0}})$. And we would further assume h small enough that ${\mathrm B}_{b h}[\zeta ]\cap \mathbb {U}_{db h}({\mathbb M})={\mathrm B}_{b h}[\zeta ]\cap \mathbb {U}_{db h}(\varphi _{i}({\omega _{i}^{2}}))$ for relevant cell centres ζ whose corresponding cells intersect $\varphi _{i}({\omega _{i}^{0}})$. Thereby we circumvent the need to use function space interpolation on submanifolds and just apply it on the parameter space, a Euclidean domain. Then, the required validity of the convergence order for integers gives that it holds in particular:

$$ \| \nabla_{{\mathrm N}} S_{h}\circ\varphi_{i}\|_{{\mathrm L}_{2}({\omega_{i}^{0}})} \le c h^{\ell -1} \| f\circ\varphi_{i}\|_{{\mathrm H}^{\ell }({\omega_{i}^{2}})}. $$

(A.4.8)

To see this, we note that the quasi-interpolation operator Q_h is local in the following sense: For sufficiently small h we have that $\| (g - f)\circ \varphi _{i}\|_{{\mathrm H}^{\ell }({\omega _{i}^{2}})}=0$ implies $\| \nabla _{{\mathrm N}}({\mathrm Q}_{h}({\mathrm {E\!\!{}x}}_{{\mathrm N}} g - {\mathrm {E\!\!{}x}}_{{\mathrm N}} f))\circ \varphi _{i}\|_{{\mathrm L}_{2}({\omega _{i}^{0}})}=0$ for any $g\in {\mathrm H}^{\ell }({\mathbb M})$. This is a consequence of the required locality of quasi-interpolation operator Q_h and the choice of the ${\omega _{i}^{0}},{\omega _{i}^{2}}$.

For the actual proof of the fractional case, we can now proceed via the so-called interpolation property for fractional Sobolev spaces (cf. [33, Th. 1.1.6], [43, Th. 6.30], [9, Def. 2.4.1], [46, Sect. 2.4.1]):

Lemma 8

Let ${\Omega }_{1},{\Omega }_{2}\subseteq {\mathbb R}^{d}$ be sets with a smooth or without a boundary. Let r = 𝜃r₁ + (1 − 𝜃)r₂ for 𝜃 ∈ (0, 1) and reals $0\le r_{1}\le r_{2}<\infty$ and let ϱ = 𝜃ϱ₁ + (1 − 𝜃)ϱ₂ for reals $0\le {\varrho }_{1}\le {\varrho }_{2}<\infty$. If ${\mathrm {\Lambda }}:{\mathrm H}^{r_{i}}({\Omega }_{1})\mapsto {\mathrm H}^{{\varrho }_{i}}({\Omega }_{2})$ is bounded for i = 1, 2, then ${\mathrm {\Lambda }}:{\mathrm H}^{r}({\Omega }_{1})\mapsto {\mathrm H}^{{\varrho }}({\Omega }_{2})$ is bounded as well and

$$ \| {\mathrm {\Lambda}}\|_{{\mathrm H}^{r}\to{\mathrm H}^{{\varrho}}}\le c\| {\mathrm {\Lambda}}\|_{{\mathrm H}^{r_{1}}\to{\mathrm H}^{{\varrho}_{1}}}^{\theta} \| {\mathrm {\Lambda}}\|_{{\mathrm H}^{r_{2}}\to{\mathrm H}^{{\varrho}_{2}}}^{(1-\theta)}. $$

Now we apply the interpolation property to ${\mathrm {\Lambda }}={\mathrm {T\!\!{}r}}_{{\mathbb M}}\nabla _{{\mathrm N}}{\mathrm Q}_{h} {\mathrm {E\!\!{}x}}_{{\mathrm N}}$. First, we choose suitable integers r₁ = ⌊r⌋, r₂ = ⌈r⌉. Then we choose 0 < 𝜃 < 1 such that r = 𝜃r₁ + (1 − 𝜃)r₂. We obtain for ϱ₁ = ϱ₂ = 0 in the interpolation property for the operator ${\mathrm {T\!\!{}r}}_{{\mathbb M}}\nabla _{{\mathrm N}}{\mathrm Q}_{h} {\mathrm {E\!\!{}x}}_{{\mathrm N}}$ the relation

$$ \begin{array}{@{}rcl@{}} \| (\nabla_{{\mathrm N}} S_{h})\circ\varphi_{i}\|_{{\mathrm L}_{2}({\omega_{i}^{0}})}&\le c h^{\theta(r_{1} - 1)+(1-\theta)(r_{2} - 1)}\| f\circ\varphi_{i}\|_{{\mathrm H}^{r }({\omega_{i}^{2}})}\\ &\le c h^{m -{\varrho}}\| f\circ\varphi_{i}\|_{{\mathrm H}^{r }({\omega_{i}^{2}})}. \end{array} $$

The presence of the operation “$\circ {}\varphi _{i}$” therein does no harm, as we can always demand that an arbitrary $g\in {\mathrm H}^{ r }({\omega _{i}^{2}})$ has the form $g=\tilde g\circ \varphi _{i}$. This gives the desired fractional relation.

1.4.4 A.4.4 Corollary 1

This corollary deals with the fact that it is also important to have approximation results just for the approximation of the normal derivatives in the ambient space. Effectively, we have already provided most of the necessary steps in the proof of Appendix 6.4.2, but we recapitulate the relevant arguments here briefly: For any tubular neighbourhood $\mathbb {U}_{h}({\mathbb M})$ that is sufficiently narrow and $r\in {\mathbb N}$ we have the relation

$$ \begin{array}{@{}rcl@{}} \left|\!\!{\kern2.2pt}\left| \nabla_{{\mathrm N}} ({\mathrm Q}_{h} {\mathrm{E\!\!{\kern2.8pt}x}}_{{\mathrm N}} f)\right|\!\!{\kern2.2pt}\right|_{{\mathrm L}_{2}(\mathbb{U}_{h}({\mathbb M}))}&\le& \left|\!\!{\kern2.2pt}\left| ({\mathrm Q}_{h} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f - {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f)\right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{1}(\mathbb{U}_{h}({\mathbb M}))} \\ &\le& \left|\!\!{\kern2.2pt}\left| ({\mathrm Q}_{h} {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f - {{\mathrm{E\!\!{\kern2.8pt}x}}_{\mathrm N}} f)\right|\!\!{\kern2.2pt}\right|_{\mathrm{H}^{1}(\mathrm{C}_{h}(\mathbb{U}_{h}(\mathbb{M})))}\\ &\le& c h^{r-1} \left|\!\!{\kern2.2pt}\left| f \right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{r}(\mathbb{U}_{bdh}({\mathbb M}))} \le c h^{r-1+{(d-k)}/2} \left|\!\!{\kern2.2pt}\left| f \right|\!\!{\kern2.2pt}\right|_{{\mathrm H}^{r}({\mathbb M})}. \end{array} $$

Therein, ${\mathrm C}_{h}(\mathbb {U}_{h}({\mathbb M}))$ is the set of all cells that intersect $\mathbb {U}_{h}({\mathbb M})$, clearly also a superset of the cells ${\mathrm C}_{h}({\mathbb M})$ that intersect ${\mathbb M}$ itself. The first inequality in the second line is due to Lemma 7 and the same summation argument as in (A.4.7), while the second inequality is due to Lemma 6. To deduce the fractional relation with $f\in {\mathrm H}^{r}({\mathbb M})$ for $r\notin {\mathbb N}$, we just have to apply the interpolation property from Lemma 8 once more.