A Bayesian model and numerical algorithm for CBM availability maximization

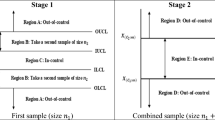
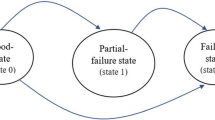
Abstract

In this paper, we consider an availability maximization problem for a partially observable system subject to random failure. System deterioration is described by a hidden, continuous-time homogeneous Markov process. While the system is operational, multivariate observations that are stochastically related to the system state are sampled through condition monitoring at discrete time points. The objective is to design an optimal multivariate Bayesian control chart that maximizes the long-run expected average availability per unit time. We have developed an efficient computational algorithm in the semi-Markov decision process (SMDP) framework and showed that the availability maximization problem is equivalent to solving a parameterized system of linear equations. A numerical example is presented to illustrate the effectiveness of our approach, and a comparison with the traditional age-based replacement policy is also provided.

Appendices

Appendix 1

The Kolmogorov’s backward differential equations are given by:

Taking Laplace transform of the above equations gives:

where $\tilde{P}_{ij}(s): = \int_{0}^{\infty} e^{ -st}P_{ij}(t)dt$ denotes the Laplace transform of P _ij (t). Solving for $\tilde{P}_{ij}(s)$ gives:

where:

Taking the inverse Laplace transform of above equation gives:

Finally, using the fact that $\sum_{j \in S_{X}} P_{ij}(t) = 1$, i=0,1, the probability transition matrix is explicitly given by  (3).

Appendix 2

Provost and Rudiuk (1996) showed that any indefinite quadratic form in normal vectors Q=U ^T AU, where U∼N _d (μ,Σ), can be expressed as the difference of two linear combinations of independent non-central chi-square variables. In particular, let Σ=LL ^T, and λ ₁,…,λ _d denote the eigenvalues of L ^T AL. Then:

where $W = \sum_{i = 1}^{p} \lambda_{i}\chi_{1}^{2}(\delta_{i}^{2})$ and $V= \sum_{i = p + 1}^{k} ( - \lambda_{i})\chi_{1}^{2}(\delta_{i}^{2})$, and eigenvalues λ _i >0 for i=1,…,p,λ _i <0 for i=p+1,…,k, and λ _i =0 for i=k+1,…,d. The random variables $\chi_{1}^{2}(\delta_{i}^{2})$ are distributed i.i.d. chi-square with one degree of freedom and non-centrality parameter $\delta_{i}^{2}$. Using this fact, the authors were able to derive an explicit formula for the exact distribution function of Q=U ^T AU, which is stated below.

Theorem 1

(Provost and Rudiuk 1996)

Let $Q = W - V = \sum_{j = 1}^{t} l_{j}T_{j} - \sum_{j = t + 1}^{t + w}l_{j}T_{j}$ where l _j are positive real numbers and the T _j are independent non-central chi-square variables with α _j degrees of freedom and non-centrality parameter d _j ,j=1,…,t+w. Let $\alpha = \sum_{j = 1}^{t} \alpha_{j} / 2$ and $\alpha ' = \sum_{j = t+ 1}^{t + w} \alpha_{j} / 2$, and b=(β ⁻¹+β′⁻¹)/2, where β and β′ satisfy that |1−β/l _j |<1,j=1,…,t, and |1−β′/l _j |<1,j=t+1,…,t+w. Then provided α and α′ are not both nonnegative integers plus 1/2, for q≤0, the distribution function of Q is given by:

and for q>0, the distribution function of Q is given by:

where constants are given by: