Sourcing from suppliers with random yield for price-dependent demand

Abstract

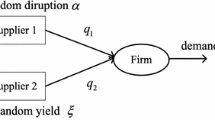
We study a multi-period inventory planning problem. In each period, the firm under consideration can source from two possibly unreliable suppliers for a price-dependent demand. Our analysis suggests that the optimal procurement policy is neither a simple reorder-point policy nor a complex one without any structure, as previous studies suggest. Instead, we prove the existence of a reorder point for each supplier. No order is placed to that supplier for any inventory level above the reorder point and a positive order is issued to that supplier for almost every inventory level below the reorder point. We characterize conditions under which the optimal policy reveals monotone response to changes in the inventory level. Furthermore, two special cases of our model are examined in detail to demonstrate how our analysis generalizes a number of well-known results in the literature.

Appendix: Proofs

Proof of Lemma 1

When t=T, we have V _T+1(I)=0 and

$$J_T(I,q_1,q_2,d) = R(d) - c_1q_1 - c_2q_2 - \mathbb {E}H (I + u_1 q_1 + u_2 q_2-\varepsilon d - \omega)$$

is concave. Because concavity is preserved under maximization, V _T (I) is concave. Now suppose that V _t+1(I) is concave. It follows immediately that J _t (I,q ₁,q ₂,d) is concave and thus V _t (I) is concave. It then follows that L _t (y) is concave and thus $J^{B}_{t}(I,q_{1},q_{2}, d)$ is jointly concave.

Since L _t in (4) is concave, L _t (I+u ₁ q ₁+u ₂ q ₂−εd) is submodular in (I,q _i ) and supermodular in (q _i ,d) and (I,d), i=1,2. Hence, J _t and $J_{t}^{B}$ are submodular in (I,q _i ) and supermodular in (q _i ,d) and (I,d). □

Lemma A.1

Suppose that F(I,q ₁,q ₂,d) is jointly concave in (I,q ₁,q ₂,d). Let

Then $q_{1}^{*}(I)$, $q_{2}^{*}(I)$, and d ^∗(I) are continuous in I.

Proof

By definition, $(q_{1}^{*}(I), q_{2}^{*}(I), d^{*}(I))$ is a maximizer of F(I,q ₁,q ₂,d). Because F(I,q ₁,q ₂,d) is jointly concave in (I,q ₁,q ₂,d), Θ is a convex set (Bertsimas and Tsitsiklis 1997). Therefore, $q_{1}^{*}(I) = \min_{\tilde{q}_{1}}\{\tilde{q}_{1} | (I,\tilde{q}_{1}, \tilde{q}_{2}, \tilde{d}) \in \Theta\}$ is continuous in I.

Now we note that $F(I, q^{*}_{1}(I), q_{2}, d)$ is jointly concave in (I,q ₂,d). Let

$$\Theta_1 = \Bigl\{(I, \tilde{q}_2, \tilde{d})| F(I, q_1^*(I), \tilde{q}_2, \tilde{d} ) = \max_{ q_2\geq0, \underline{\underline{d}}\leq d\leq\overline{\overline{d}}} F(I, q_1, q_2, d)\Bigr\}.$$

Then Θ₁ is a convex set and $q_{2}^{*}(I) = \min\{\tilde{q}_{2}|(I,\tilde{q}_{2}, \tilde{d}) \in\Theta_{1}\}$ is continuous in I.

Finally, we have $F(I, q^{*}_{1}(I), q^{*}_{2}(I), d)$ being jointly concave in (I,d). Let

$$\Theta_2 = \Bigl\{\tilde{d}| F(I, q_1^*(I), q_2^*(I), \tilde{d} ) =\max_{\underline{\underline{d}}\leq d \leq\overline{\overline {d}}} F(I, q_1, q_2, d)\Bigr\}.$$

Then Θ₂ is a convex set and $d^{*}(I) = \min\{\tilde{d} |(I,\tilde{d}) \in\Theta_{2}\}$ is continuous in I. □

Proof of Lemma 2

Define $y_{1} = I + \bar{u}_{1} q_{1}$ and

(8)

We observe that the right-hand side does not depend on I and is concave in (y ₁,q ₂,d). Let $\tilde{d}(y_{1})$ and $\tilde{q}_{2}(y_{1})$ denote the maximizer of Φ _t for a given y ₁. It follows that $\Phi_{t}(y_{1}, \tilde{q}_{2}(y_{1}), \tilde{d}(y_{1}))$ is concave in y ₁ and has a maximizer, which we denote by $\bar{y}^{B}_{t,1}$. We also denote $\bar{q}^{B}_{t,2}=\tilde{q}_{2}^{B}(\bar{y}^{B}_{t,1})$ and $\bar{d}^{B}_{t}=\tilde{d}(\bar{y}^{B}_{t,1})$. Thus, the optimal ordering decision for supplier 1 follows a base-stock policy, i.e., $q^{B}_{t,1}(I) = (\bar{y}^{B}_{t,1} - I)^{+}/\bar{u}_{1}$. Moreover, when $I \leq\bar{y}^{B}_{t,1}$, we must have $I+\bar{u}_{1} q^{B}_{1} (I) = \bar{y}^{B}_{t,1}$, which implies $q^{B}_{t,2}(I) =\tilde{q}_{2}^{B}(\bar{y}^{B}_{t,1}) = \bar{q}^{B}_{t,2}$ and $d^{B}_{t}(I) = \tilde{d}(\bar{y}^{B}_{t,1}) = \bar{d}^{B}_{t}$. □

Proof of Lemma 3

We suppose $q^{*}_{t,1}(I)> 0$ and $q^{B}_{t,1}(I)=0$. Then, we must have

The first inequality follows from the facts that for model $\mathcal {G}$, $(0, q^{B}_{t,2}(I), d^{B}_{t}(I))$ is a feasible solution and $(q^{*}_{t,1}(I), q^{*}_{t,2}(I), d^{*}_{t}(I))$ is the optimal solution. The second inequality follows from the concavity of L _t and Jensen’s inequality. If the inequality is strict, then the above relation suggests that in model $\mathcal{B}$, $(q^{*}_{t,1}(I),q^{*}_{t,2}(I), d^{*}_{t}(I))$ yields a higher profit than $(0,q^{B}_{t,2}(I),d^{B}_{t}(I))$. This contradicts the optimality of $(0,q^{B}_{t,2}(I),d^{B}_{t}(I))$. If equality holds in the above relation, then $q^{*}_{t,1}(I) = 0$ is also an optimal solution. Therefore, we conclude the proof. □

Proof of Lemma 4

We prove the result for supplier 1 and that for supplier 2 follows in a similar way. To see (i), we note that $\tilde{q}_{t,1}(I)<0$ implies, for a small enough δ,

The second inequality follows from Jensen’ inequality. The last inequality follows from the maximality of V _t (I−δ). Hence, we obtain part (i).

We show part (ii) by contradiction. There does not exists a δ>0 satisfying $\frac{V_{t}(I+\delta)- V_{t}(I)}{\delta} \geq c_{1}$. We must have $\frac{V_{t}(I+\delta)- V_{t}(I)}{\delta} < c_{1}$ for any δ≥0 and thus for any $\delta\in[0, q^{*}_{t,1}(I) \overline {\overline{u}}_{1}]$. It follows, for each realization of $u_{1} = \check{u}_{1} \neq0$,

(9)

The second inequality follows from the maximality of V _t . Taking expectation over $\check{u}_{1}$, we obtain

Since equality holds in the above relation, we must have equality in (9) for each $\check{u}_{1}$. It follows that V _t (I+δ)−V _t (I)=c ₁ δ for $\delta\in[0, q^{*}_{t,1}(I)\overline{\overline{u}}_{1}]$. This leads to a contradiction. □

Proof of Lemma 5

The result would follow if there exists an $I^{UB}_{t}$ such that $q^{*}_{i,t}(I) =0$, i=1,2, for any $I \geq I^{UB}_{t}$. Note from Lemma 4(ii) and the concavity of V _t (I), $q^{*}_{i,t}(I) =0$ if $\frac{V_{t}(I+\delta )-V_{t}(I)}{\delta} \leq\min\{c_{1},c_{2}\} = c_{1}$ for any δ>0. We show that there exists an $I^{UB}_{t}$ such that $\frac{V_{t}(I+\delta )-V_{t}(I)}{\delta} \leq\min\{c_{1},c_{2}\} = c_{1}$ for $I \geq I^{UB}_{t}$ and any δ>0. This is clearly true for period T+1. Suppose it is true for period t+1. Note that $\frac{H(I+\nu)-H(I)}{\nu} \geq 0$ for I≥0 and ν>0. Hence, there exists an $I^{UB}_{t}$ such that

$$\frac{\mathbb {E}[L_t(I^{UB}_t+\delta- \varepsilon\overline{\overline{d}})- L_t(I^{UB}_t - \varepsilon\overline{\overline{d}}) ]}{\delta}\leq0 + \alpha c_1 \leq c_1.$$

This implies

Hence, we conclude the proof. □

Proof of Lemma 6

We prove the result by contradiction. Suppose that the result is not true. Then by the continuity of $q^{*}_{1,t}(I)$ established in Lemma A.1, there exists a γ ⁻ such that $q^{*}_{t,1}(\bar{I}-\delta_{1}) =0$ for any δ ₁∈(0,γ ⁻). Now choose a $\delta_{1} \in[\underline{\delta}, \overline {\delta}] \in(0, \gamma^{-})$ satisfying $\underline{\delta} <\overline{\delta}$. Because $q^{*}_{t,1}(\bar{I}-\delta_{1})=0$, we must have

Because $q^{*}_{t,1}(\bar{I} +\delta) >0$, we have from Lemma 3, $q^{B}_{t,1}(\bar{I}+\delta) >0$ and thus $q^{B}_{t,1}(\bar{I} - \delta_{1}) >0$. Moreover, from Lemma 2, we must have the base-stock level $\bar{y}^{B}_{t,1} >\bar{I}$, and $q^{B}_{t,1}(I) = (\bar{y}^{B}_{t,1} - I )/\bar{u}_{1}$ for $I\leq\bar{I}$. Now define $\tilde{J}_{t}^{B}(I, q_{1}) = \max_{q_{2} \geq0,\underline{\underline{d}}\leq d \leq\overline{\overline{d}}} J^{B}_{t}(I, q_{1}, q_{2}, d)$. Then $\tilde{J}_{t}^{B}(I, q_{1})$ is jointly concave in (I,q ₁) and the smallest maximizer of $\tilde{J}_{t}^{B}(\bar{I}-\delta _{1}, q_{1})$ is $q^{B}_{t,1}(\bar{I} - \delta_{1}) = (\bar{y}^{B}_{t,1} - \bar{I}+ \delta_{1})/\bar{u}_{1} > \delta_{1}/\bar{u}_{1}$. Therefore,

(10)

where $\kappa= \tilde{J}_{t}^{B}(\bar{I}, 0) - \tilde{J}_{t}^{B}(\bar{I},-\underline{\delta}/\bar{u}_{1}) >0$ as the base-stock level $\bar{y}^{B}_{t,1} > \bar{I}$. To see the second equality, we note that $\kappa=\tilde{J}_{t}^{B}(\bar{I} - \delta_{1}, \delta_{1}/\bar{u}_{1}) - \tilde{J}^{B}_{t}(\bar{I} -\delta_{1}, (\delta_{1} - \underline{\delta}) / \bar{u}_{1})\leq \tilde{J}_{t}^{B}(\bar{I} - \delta_{1}, \delta_{1}/\bar{u}_{1}) - \tilde{J}^{B}_{t}(\bar{I} -\delta_{1}, 0)$. Therefore, (10) implies

$$ V_t(\bar{I}) -V_t(\bar{I}-\delta_1) > c_1 \delta_1.$$

(11)

Let $\tilde{q}_{t,1}(I)$ be the smallest unconstrained maximizer of $J_{t}(I, q_{1}, q^{*}_{t,2}(I), d^{*}_{t}(I))$. Because $q_{t,1}^{*}(\bar{I} -\delta_{1}) =0$, we must have $\tilde{q}_{t,1}(\bar{I}-\delta_{1}) \leq0$. Now if $\tilde{q}_{t,1}(\bar{I} -\delta_{1}) <0$, then from Lemma 4 and the concavity of V _t (I), we have $V_{t}(\bar{I}) -V_{t}(\bar{I} -\delta_{1}) \leq c_{1} \delta_{1}$, which contradicts (11). Hence, we obtain $\tilde{q}_{t,1}(\bar{I} - \delta _{1}) = 0$ for $\delta_{1} \in[\underline{\delta},\overline{\delta}]$.

Now we note that V _t is concave so that there can be at most countable points at which V _t is not differentiable (Phelps 1993). For a differentiable point $I \in[\bar{I} - \overline {\delta}, \bar{I} - \underline{\delta}]$, we have

is well defined. Because $\tilde{q}_{t,1}(I) = 0$, we derive by the envelope theorem

This implies that $V^{\prime}_{t}(I) = \bar{c}_{1}/\bar{u}_{1} = c_{1}$. This contradicts (11). □

Proof of Lemma 7

Because V _t (I) is concave, it can have at most countable number of non-differentiable points. Let N denote the set of non-differentiable points. We show that X ₁⊂N. Suppose this is not true. Then there exist an $\bar{I}$ with $V^{\prime}_{t}(I)$ well-defined over the neighborhood of $\bar{I}$ such that $\bar{I}$ satisfies the conditions in Lemma 6. In other words, $q^{*}_{t,1}(\bar{I}) = 0$ and $q^{*}_{t,1}(\bar{I} +\delta) >0$ for any arbitrarily small δ. From the proof of Lemma A.1, $\tilde{q}_{1,t}(I)$ is continuous. Hence, we must have $\tilde{q}_{t,1}(\bar{I})= q^{*}_{t,1}(\bar{I}) =0$. By the envelope theorem, we have

$$V^\prime_t(\bar{I}) = \frac{\partial \mathbb {E}L_t(\bar{I} + u_2q_{t,2}^*(\bar{I}) -\varepsilon d^*_t(\bar{I}))}{\partial\bar{I}}.$$

Hence, the right-hand side of the above is well defined. The first-order condition of $\tilde{q}_{t,1}(\bar{I})=\nobreak 0$ leads to

$$- \bar{c}_1 + \bar{u}_1 \frac{\partial \mathbb {E}L_t(\bar{I} + u_2q_{t,2}^*(\bar{I}) -\varepsilon d^*_t(\bar{I}))}{\partial\bar{I}} = 0.$$

Now consider the benchmark problem $\mathcal{B}$. The above relation implies that

$$\frac{\partial J^B_t(\bar{I}, q_1,q_{t,2}^*(\bar{I}), d^*_t(\bar{I}))}{\partial q_1}\bigg|_{q_1=0} = - \bar{c}_1 + \bar{u}_1\frac {\partial \mathbb {E}L_t(\bar{I} + u_2 q_{t,2}^*(\bar{I}) -\varepsilon d^*_t(\bar{I}))}{\partial\bar{I}} = 0.$$

It is also clear that

$$J^B_t(\bar{I}, 0,q_{t,2}^*(\bar{I}), d^*_t(\bar{I})) = \max_{q_2 \geq0,\underline{\underline{d}} \leq d \leq\overline{\overline{d}}}J^B_t(\bar{I}, 0,q_2, d).$$

Therefore, $q^{B}_{t,1}(\bar{I}) = 0$, $q^{B}_{t,2}(\bar{I}) = q_{t,2}^{*}(\bar{I})$ and $d^{B}_{t}(\bar{I}) = d^{*}_{t}(\bar{I})$. By Lemma 2, we must have $q^{B}_{t,1}(I) = 0$ for any $I \geq\bar{I}$. Moreover, by Lemma 3, we deduce that $q^{*}_{t,1}(I) = 0$ for any $I \geq\bar{I}$. This leads to a contradiction. □

Lemma A.2

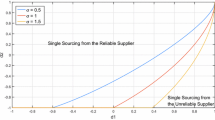
If the pricing decision is made before observing (u ₁,u ₂) and after observing (ε,ω), then the optimal price is decreasing in the inventory level and the optimal orders follow a near reorder-point policy.

Proof

Let $\tilde{V}_{t}(I)$ be the optimal profit function in period t when the inventory level is I. The optimality equation is given by

Note that $\tilde{J}_{t}(I,q_{1},q_{2},d)$ is supermodular in (I,d). Hence, the optimal price is increasing in I. Finally, the optimal ordering decisions can be derived in a way similar to that of Theorem 1. □

Proof of Theorem 2

To see part (i), we note that the optimal profit function V _t (I) is differentiable in I when εd+ω has a continuous distribution. The result follows immediately from the proof of Lemma 7.

For part (ii-a), we first show that $d^{*}_{t}(I)$ is increasing in I. We have

$$V_t(I)= \max_{d \in[\underline{\underline{d}} ,\overline{\overline {d}}]} \{R(d) + G_t(I-d)\}, $$

(12)

where

$$G_t(z)= \max_{ q_1 \geq0, q_2 \geq0}\{ - \bar{c}_1 q_1 - \bar{c}_2 q_2+ \mathbb {E}L_t(z + u_1 q_1 + u_2 q_2)\}.$$

Since L _t is concave, it is clear that G _t (z) is concave in z and thus G _t (I−d) is supermodular. We deduce that R(d)+G _t (I,d) is supermodular, which leads to the desired result.

Next we prove that the change in $d^{*}_{t}(I)$ is less than the corresponding change in I. We can write (12) as

$$V_t(I)= \max_{z \in[I- \overline{\overline{d}}, I - \underline {\underline{d}}] } R(I - z) + G_t(z).$$

Since R and G _t are concave, R(I−z)+G _t (z) is supermodular in (I,z). It follows that the maximizer $z_{t}^{*}(I)= I-d^{*}_{t}(I)$ is increasing in I. Hence, we obtain the desired result.

To prove part (ii-b), let $\theta_{i}=\operatorname{Pr}\{u_{i} = \overline {\overline{u}}_{i}\}$, i=1,2, and z=I−d. We have

$$J_t(I, q_1, q_2, I-z) = R(I-z) + (1-\theta_1)(1-\theta_2) L_t(z) +\overline{G}_t(z, q_1, q_2),$$

where

Note that for fixed (I,d), the optimal (q ₁,q ₂) maximizes $\overline{G}_{t}(z, q_{1}, q_{2})$ and depends on (I,d) only via z=I−d. Now define $y_{1} = z + \overline{\overline{u}}_{1} q_{1}$. Then,

(13)

where

$$Q(z, q_2) = \max_{y_1 \geq z} - c_1\theta_1 y_1 + \theta _1(1-\theta_2) L_t(y_1)+ \theta_1\theta_2 L_t(y_1 + \overline{\overline{u}}_2 q_2).$$

Let $\bar{y}_{1}(q_{2})$ denote the unconstrained maximizer of Q(y ₁,q ₂). Then, for given (z,q ₂) the optimal y ₁ is $\max\{\bar{y}_{1}(q_{2}),z\}$. It is easily seen that Q(y ₁,q ₂) is jointly concave and thus Q(z,q ₂) is concave. If $\bar{y}_{1}(q_{2}) \geq z$, then Q(z,q ₂) submodular in (z,q ₂) because L _t is concave. If, however, $\bar{y}_{1}(q_{2}) < z$, then Q(z,q ₂) is concave in q ₂ and constant in z. In either case, the function inside the maximum of (13) is submodular in (q ₂,z) and thus the optimal q ₂(z) is decreasing in z. We further recall part (i) that the optimal $z^{*}_{t}(I) = I - d^{*}_{t}(I)$ is increasing in I. We deduce that $q_{2,t}^{*}(I) = q_{2}(z^{*}_{t}(I))$ is decreasing in I. Now note that $q^{*}_{1,t} (I) = \max\{\bar{y}_{1}(q_{2}(z^{*}_{t}(I)))-z_{1}^{*}(I), 0\}/\overline{\overline{u}}_{1}$. Since $q^{*}_{1,t}=0$ when $I \geq I^{*}_{t,1}$, we focus on the case $I < I^{*}_{t,1}$. Let $y_{2} = z +\overline{\overline{u}}_{2} q_{2}$. For $I < I^{*}_{t,1}$,

(14)

where

$$\tilde{Q}(q_2) = \max_{y_1} \{- c_1\theta_1 q_1 + \theta_1(1-\theta_2) L_t(y_1)+ \theta_1\theta_2 L_t(y_1 + \overline{\overline{u}}_2 q_2) \}.$$

Because L _t is concave, $\tilde{Q}$ is concave. It follows that the function inside the maximum of (14) is supermodular in (y ₂,z) and thus the optimal y ₂(z) is increasing in z. We further recall part (i) that the optimal $z^{*}_{t}(I) = I - d^{*}_{t}(I)$ is increasing in I. We deduce that $z^{*}_{t}(I)+ \overline{\overline{u}}_{2} q^{*}_{2,t}(I)$ is increasing in I. Also, we can rewrite $\tilde{Q}$ as follows,

$$\tilde{Q}(q_2) = \max_{q_1}\{ - c_1\theta_1 q_1 + \theta_1(1-\theta _2) L_t( z + \overline{\overline{u}}_1 q_1)+ \theta_1\theta_2 L_t(z + \overline{\overline{u}}_2 q_2 +\overline {\overline{u}}_1 q_1)\}. $$

(15)

The function inside the maximum of (15) is submodular in (z,q ₁) and $(z + \overline{\overline{u}}_{2} q_{2} , q_{1})$. Because both $z^{*}_{t}(I)+\overline{\overline{u}}_{2} q^{*}_{2,t} (I)$ and $z^{*}_{t}(I)$ increase in I, $q^{*}_{1,t} (I)$ decrease in I. We conclude the proof. □

Proof of Theorem 3

We prove the result using contradiction by assuming that $q^{*}_{t,2}(I^{a}) \leq q^{*}_{t,2}(I^{b})$. We must have

The first inequality follow from the optimality of $(q^{*}_{t,1}(I^{b}),q^{*}_{t,2}(I^{b}))$ for J _t (I ^b,q _t,1,q _t,2,d _t ). The second inequality follows from the concavity of L _t . The third equality comes from the optimality of $(q^{*}_{t,1}(I^{a}),q^{*}_{t,2}(I^{a}))$ for J _t (I ^a,q _t,1,q _t,2,d _t ).

Moreover, in the view of above proof, we can obtain that the results of (i) and (ii-a) hold for multiple suppliers and the result of (ii-b) only holds for two suppliers. We conclude the proof. □

Proof of Theorem 4

Suppose that $d^{*}_{t}(I^{a}) \geq d^{*}_{t}(I^{b})$ and $q^{*}_{t,1}(I^{a}) <q^{*}_{t,1}(I^{b})$ for I ^a<I ^b. Then we must have

The first inequality follow from the optimality of $(q^{*}_{t,1}(I^{b}),d^{*}_{t}(I^{b}))$ for J _t (I ^b,q _t,1,0,d _t ). The second inequality follows from the concavity of L _t . The third equality comes from the optimality of $(q^{*}_{t,1}(I^{a}),d^{*}_{t}(I^{a}))$ for J _t (I ^a,q _t,1,0,d _t ). We reach a contradiction. We conclude the proof. □

Proof of Theorem 5

If a=0, then u ₁=b is deterministic. From Lemma 2, we know $q^{*}_{t,1}(I)$ follows a base-stock policy and is thus decreasing in I. Now note that for $I \leq\bar{y}^{B}_{t,1}$, $q^{*}_{t,2}(I) = \bar{q}^{B}_{t,2}$ is constant in I. For $I > \bar{y}^{B}_{t,1}$, we have $q^{*}_{t,1}(I) = 0$ and J _t (I,0,q ₂,d) is submodular in (I,q ₂) by Lemma 1. Hence, $q^{*}_{t,2}(I)$ is decreasing in I. In particular, if a=b=0, then u ₁=0. In this case, the problem reduces to one with only supplier 2 and thus $q^{*}_{t,2}(I)$ is decreasing in I as pointed out by Henig and Gerchak (1990).

Now we examine the case when a≠0. To see part (i), we first note that $q^{*}_{t,2}(I)=0$ for $I \geq I^{*}_{t,2}$. In this case, $q^{*}_{t,1}(I)$ is decreasing in I since J _t (I,q ₁,0,d) is submodular in (I,q ₁) by Lemma 1. If $I< I^{*}_{t,2}$, then $q^{*}_{t,2}(I) = \tilde{q}_{t,2}(I)$ where $\tilde{q}_{t,2}(I)$ is defined in Lemma 4. Now define x≡aq ₁+q ₂ (or q ₂=x−aq ₁) and $\mathcal{J}_{t}(I, q_{1}, x) =J_{t}(I, q_{1}, x-a q_{1}, d)$. Also let $\mathcal{W}_{t}(I,q_{1})= \max _{x}\mathcal{J}_{t}(I,q_{1},x)$ with $\tilde{x}(I,q_{1})$ denoting the corresponding maximizer. It is easily seen that $\mathcal{J}_{t}$ is concave and thus $\mathcal{W}_{t}$ is concave. The result would follow provided that $\mathcal{W}_{t}(I,q_{1})$ is submodular in (I,q ₁), i.e. for any I ^a≤I ^b and $q_{1}^{a}\leq q_{1}^{b}$,

$$ \mathcal{W}_t(I^a,q_1^a) + \mathcal{W}_t(I^b,q_1^b) \leq\mathcal {W}_t(I^a,q_1^b) + \mathcal{W}_t(I^b,q_1^a).$$

(16)

It is clear that (16) holds when I ^a=I ^b. Therefore, we focus on the case when I ^a<I ^b. Define $x^{a}=\tilde{x}(I^{a},q_{1}^{a})$ and $x^{b}=\tilde{x}(I^{b},q_{1}^{b})$. We deduce

(17)

The inequality follows from the maximality of $\mathcal{W}_{t}$.

Moreover, by the concavity of $\mathcal{W}_{t}(I,q)$, we obtain

(18)

(19)

Relations in (17), (18) and (19) imply

$$\frac{\mathcal{W}_t(I^b,q_1^b) - \mathcal{W}_t(I^a,q_1^b)}{I^b - I^a}\leq \frac{\mathcal{W}_t(I^b,q_1^a) - \mathcal{W}_t(I^a,q_1^a)}{I^b - I^a},$$

which leads to (16).

To see part (ii), we note that $u_{2} = - \frac{1}{a} u_{1} - \frac{b}{a}$. Hence, a similar argument as that in part (i) yields the result.

To see parts (iii), we note that u ₁=au ₂ when b=0. We have

The right-hand side is separable in q ₁ and x. Hence, the optimal $x^{*}_{t}(I)$ maximizes the last two terms for x≥0. Since L _t is concave, it is clear that $x^{*}_{t}(I)$ is decreasing in I. Also $q^{*}_{t,1}(I)$ maximize $a \bar{u}_{2}( c_{2}- c_{1}) q_{1}$ over $q_{1} \in[0,x^{*}_{t}(I)/a]$. If c ₂≥c ₁, we must have $q^{*}_{t,1}(I)=x^{*}_{t}(I)/a$ is decreasing in I, which, in turn, implies $q^{*}_{t,2}(I) = x^{*}_{t}(I) - a q^{*}_{t,1}(I) = 0$. If, however, c ₂<c ₁, then $q^{*}_{t,I} = 0$ and $q^{*}_{t,2}(I) = x^{*}_{t}(I)$ is decreasing in I.

For $b = -a (\overline{\overline{u}}_{2} + \underline{\underline {u}}_{2})$ and a<0, we have $q^{*}_{t,1}(I)$ is decreasing in I from the part (i). From the Theorem 1, Lemma 4 and the fact c ₁≤c ₂, we know that $\tilde{q}_{t,1}(I)\geq0$ and $\tilde{q}_{t,2}(I)\geq0$ when $I\leq I^{*}_{t,2}$. From the continuity of $q^{*}_{t,2}(I)$, we only need to prove that there exists $\bar{q}_{t,2}$ and an optimal solution satisfying that $q^{*}_{t,2}(I)= \bar{q}_{t,2} - \frac{I}{\overline{\overline{u}}_{2} +\underline{\underline{u}}_{2}}$ when $I\leq I^{*}_{t,2}$. Define $y_{1} =I - a (\overline{\overline{u}}_{2} + \underline{\underline{u}}_{2})q_{1}$ and

We observe that the right-hand side does not depend on I and is concave in (y ₁,x). Let $(\bar{y}_{1}, \bar{x})$ to denote the maximizer of Φ _t . We must exist an optimal solution satisfying $I - a(\overline{\overline{u}}_{2} + \underline{\underline{u}}_{2}) q^{*}_{1}(I)= \bar{y}_{1}$ and $a q^{*}_{1}(I) + q^{*}_{2}(I) = \bar{x}$ when $I\leq I^{*}_{t,2}$. Define $\bar{q}_{t,2} = \bar{x} + \frac{\bar{y}_{1}}{\overline {\overline{u}}_{2} + \underline{\underline{u}}_{2}}$. Thus, $q^{*}_{2}(I) =\bar{x} - a q^{*}_{1}(I) = \bar{x} - \frac{I- \bar{y}_{1}}{\overline{\overline {u}}_{2} + \underline{\underline{u}}_{2}} = \bar{q}_{t,2} - \frac {I}{\overline{\overline{u}}_{2} + \underline{\underline{u}}_{2}}$. We conclude the proof. □

Proof of Theorem 6

The proof is similar to the one for Theorem 5. The added complexity here is that we have to consider the decision d _t (I) which is bounded from above. □

Example 3

(Li and Zheng 2006)

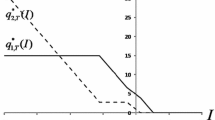
T=1, c ₁=1, H(x)=h(max{x,0})²+s(max{−x,0})² with h=2, s=9, p(d)=20−d, Pr {u ₂=0}=1, Pr {ε=0}=Pr {ε=2}=0.5 and ω=0. The yield rate u ₁ is uniform (0,0.5). See Fig. 3.

Fig. 3

The example provided in Li and Zheng (2006)