Lifetime properties of a cumulative shock model with a cluster structure

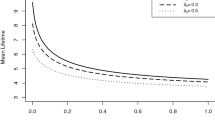
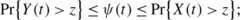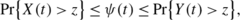Abstract

This paper studies a generalized cumulative shock model with a cluster shock structure. The system considered is subject to two types of shocks, called primary shocks and secondary shocks, where each primary shock causes a series of secondary shocks. The lifetime behavior of such a system becomes more complicated than that of a classical model with only one class of shocks. Under a non-homogeneous Poisson process of primary shocks, we analyze the lifetime behavior of the system with light-tailed and heavy-tailed distributed secondary shocks. We show some important characteristics of lifetime of this type of system. Our model, as an extension of the classical shock models, has wide applications in maintenance engineering, operations management, and insurance risk assessment.

Appendix

The proofs of Theorems 1–4 are based on some preliminaries. Using the definitions of the cumulative shock process {X(t)} and the ultimate failure probability ψ,

(A.1)

we define a new process {X′(t)}, the variant version of {X(t)}, as

$$ X^{\prime}(t)=\sum_{i=1}^{N(t)} \Biggl(rX_{i}+\sum_{j=1}^{M_{i}(C_{i})}Y_{ij}\Biggr), \quad t\geq0, $$

(A.2)

where r=−1, 0 or 1. On the relation between {X(t)} and {X′(t)}, we have the following result.

Lemma A.1

For each t>0, X′(t)≥X(t).

Lemma A.1 says that {X′(t)} is “larger” than {X(t)}. However, we can show, for an arbitrary δ>0, that

where Λ(t) is the cumulative intensity function of the primary shock process {N(t)}, and the symbol “$\xrightarrow{\mathrm{p}}$” stands for convergence in probability. It means that the difference in probability between {X(t)} and {X′(t)} becomes negligible after a long period of time.

Also, we define a discrete process {Z _n } as

(A.3)

Then Z _n is the embedded process of {X′(t)} and records the state of {X′(t)} at time instant S _n , while the nth primary shock occurs and {X′(t)} has a downward jump. It is clear that, for n=0,1,… ,

(A.4)

where $\xi_{i}=rX_{i}+\sum_{j=1}^{M_{i}(C_{i})}Y_{ij}$, i=1,2,… , are i.i.d. random variables by Assumptions (ii)–(iv).

Now we prove Theorems 1–4.

Proof of Theorem 1

When r=1 or 0, {Z _n } is a renewal process with the renewal interval

For a given z>0, define the “lifetimes” τ′ and N for the processes {X′(t)} and {Z _n }, respectively,

(A.5)

(A.6)

It is clear that τ′=S _N , where S _N is the Nth shock arrival instant of the primary process {N(t)}, and N is an almost surely finite stopping-time of {Z _n } with the discrete distribution

(A.7)

where F _ξ is the common distribution function of ξ _i and the symbol “∗” represents convolution operation.

It follows from Lemma A.1, (A.5) and (A.6) that the system lifetime τ satisfies

then

$$ E[\tau]\geq E\bigl[\tau^{\prime}\bigr]=E[S_{N}]. $$

(A.8)

Now we can estimate the lower bound of E[τ] by computing E[S _N ]. Since {N(t)} is a non-homogeneous Poisson, for s>0, we have

Hence,

Using (A.8), we have

$$ E[\tau]\geq\int_{0}^{\infty}\sum _{n=0}^{\infty}\sum_{k=0}^{n-1}p_{n} \frac{\varLambda^{k}(s)}{k!}e^{-\varLambda(s)}\,ds, $$

(A.9)

where p _n =Pr{N=n} is given by (A.7). □

Proof of Theorem 2

If {N(t)} is a homogeneous Poisson with intensity λ>0, let B _n =S _n −S _n−1, n=1,2,… , be the inter-arrival time, then E[B _n ]=1/λ. Hence,

$$ E[S_{N}]=E \Biggl[\sum_{n=1}^{N}B_{n} \Biggr]=E[N]E[B_{1}]=\frac{ 1}{\lambda}E[N]. $$

(A.10)

To find E[N], based on renewal process {Z _n } and using Wald Identity, we have

Secondly, because of exponentially distributed Y _ij with parameter μ>0, for an arbitrary x≥z, we obtain

Thus the density function of Z _N is $f_{{ Z_{N}}}(x)=\mu e^{-\mu(x-z)}$, and

Then the expected stopping-time is

$$ E[N]=\frac{z+\frac{1}{\mu}}{E[\xi_{1}]}=\frac{1+\mu z}{E[M_{1}(C_{1})]+\mu rE[X_{1}]}. $$

(A.11)

Using (A.8), (A.10) and (A.11), we have

where r=1 or 0. □

Proof of Theorem 3

In the case of r=−1, we have

where $\xi_{i}=\sum_{j=1}^{M_{i}(C_{i})}Y_{ij}-X_{i}$, i=1,2,… are i.i.d. random variables. Thus {Z _n } is a random walk starting from the origin. Also, by Assumption (v), {Z _n } is transient and has an average downward drift. Let

be the probability that {Z _n } eventually exceeds level z. Since {Z _n } is the embedded process of {X′(t)}, they have a same limiting probability. Then, it follows from Lemma A1 that the probabilities of {X(t)} and {Z _n } eventually exceeding z satisfy

$$ \psi\leq p_{Z}. $$

(A.12)

Thus we can evaluate the upper-bound of ψ by estimating p _Z . The next lemma gives an exponential-type estimation of p _Z .

Lemma A.2

Under Assumptions (ii)–(v), if $E[e^{sY_{ij}}]$ exists, then

where θ>0 is determined by the equation

(A.13)

Proof

For some y>0 and n=0,1,… , define

where θ is a positive number satisfying (A.13). Then κ is obviously a stopping time with respect to the natural filtration of {Z _n }:

and {M _n } is a martingale with respect to . Therefore, we have

By applying the martingale stopping theorem to {M _n } and κ, we have

Conditioning on Z _κ in $E[M_{\kappa}]=E[e^{\theta Z_{\kappa}}]$, we obtain

$$ E \bigl[e^{\theta Z_{\kappa}}\bigm|Z_{\kappa}>z \bigr]q+E \bigl[e^{\theta Z_{\kappa}}\bigm| Z_{\kappa}\leq-y \bigr](1-q)=1, $$

(A.14)

where q denotes the probability that the random walk {Z _n } exceeds z before it reaches −y.

Let y→∞, the second term on the left hand side of (A.14) tends to 0, then

Note that, when y goes to positive infinity, the limiting probability of {Z _n } exceeding z before reaching −y is just the probability of exceeding z, so lim _y→∞ q=p _Z (u). Using the Jensen’s Inequality, we have

This means p _Z ≤e ^−θz with θ>0 satisfying (A.13).

Using (A.12) and Lemma A.2, we complete the proof of Theorem 3. □

Proof of Theorem 4

According to the proof of Theorem 3, we need to show

(A.15)

where θ>0. For this, we take y→∞ in (A.14) and get

(A.16)

First, for the exponential distribution, we can calculate the conditional expectation of the denominator in (A.16). For some x≥0, we have

where $\sum_{n}=\sum_{n=0}^{\infty}$, p _n =Pr{κ=n}, $p_{\Delta}=\prod_{i=1}^{n}\Pr\{M_{i}(C_{i})=m_{i}\}$, $\sum_{\Delta}=\sum_{m_{1}}\sum_{m_{2}}\cdots\allowbreak \sum_{m_{n}}$, $\Delta^{\prime}=\Delta_{i=1}^{\prime n}(\sum_{j=1}^{m_{i}}Y_{ij}-X_{i})-Y_{nm_{n}}$, and F _Δ′ denotes the distribution function of Δ′. Thus we have the conditional density

and the conditional expectation

Therefore, (A.15) is obtained by putting this result in (A.16).

Next, to determine the parameter θ, we use $E[e^{\theta Y_{11}}]=\frac{\beta}{\beta-\theta}$ and get

where q _k =Pr{M ₁(C ₁)=k}. Since {M _n } is a martingale, $E[e^{\theta\xi_{1}}]=E[M_{1}]$ =E[M ₀]=1, then

That is, θ satisfies Eq. (11). □

Proof of Theorem 5

We prove Theorem 5 in several steps and start with a representation of the primary shock process,

where K _i (t)=M _i ((t−S _i )∧C _i ) and

(A.17)

Also, we rewrite ψ(t), the failure probability of the system within finite horizon (0,t] defined in (5), as

To complete the proof, we need the following two lemmas.

Lemma A.3

Given t<∞, the probability ψ(t) satisfies

• (i) for r=1,0,

  

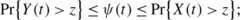
• (ii) for r=−1,

  

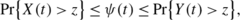
  where Y(t) is given by (A.17).

Proof

Obviously. □

Lemma A.4

Under Assumption (vii), if the magnitudes $Y_{11}^{I}$ and $Y_{11}^{\mathit{II}}$ of the two classes of adjunctive shocks have the regular-tailed distributions $F_{\alpha}^{I}(y)$ and $F_{\alpha}^{\mathit{II}}(y)$, respectively, with a common index α>0, then, for given t<∞,

Proof

The proof is based on the classification and the main technique is using the closure properties of regular-tailed distribution family. By Assumption (vii), we know that Class I and Class II of shocks are mutually independent. This implies that the primary shock process {N(t)} is formed by two independent shock processes {N ^I(t)} and {N ^II(t)} relating to the two classes, which are also non-homogeneous Poisson and satisfy N ^I(t)+N ^II(t)=N(t) for each t>0. The relation between the adjunct shock processes $\{M_{i}^{I}(t)\}$ and $\{M_{i}^{\mathit{II}}(t)\}$ is similar.

First, we calculate the probability Pr{X(t)>z}. For given t<∞,

where $K^{I}_{i}(t)=M^{I}_{i}((t-S^{I}_{i})\wedge C^{I}_{i})$, $K^{\mathit{II}}_{i}(t)=M^{\mathit{II}}_{i}((t-S^{\mathit{II}}_{i})\wedge C^{\mathit{II}}_{i})$. Conditioning on N ^I(t) and N ^II(t), denoting p _n =Pr{N ^I(t)=n}, p _m =Pr{N ^II(t)=m}, and $\sum_{s}=\sum_{s=0}^{\infty}$, the above computation continues as

where $K^{I}_{i}(U^{I}_{t})=M^{I}_{i}((t-U^{I}_{i})\wedge C^{I}_{i})$, $K^{\mathit{II}}_{i}(U^{\mathit{II}}_{t})=M^{\mathit{II}}_{i}((t-U^{\mathit{II}}_{i})\wedge C^{\mathit{II}}_{i})$, $U^{I}_{1},\dots,U^{I}_{n}$ are i.i.d. random variables defined in (0,t], and similarly $U^{\mathit{II}}_{1},\dots,U^{\mathit{II}}_{m}$ are also i.i.d random variables. Next, conditioning on $K^{I}_{i}(U^{I}_{t})$, $K^{\mathit{II}}_{i}(U^{\mathit{II}}_{t})$ respectively, denoting $q_{k_{i}}=\Pr\{K^{I}_{i}(U^{I}_{t})=k_{i}\}$ for i=1,2,…,n and $q_{l_{i}}=\Pr\{K^{\mathit{II}}_{i}(U^{\mathit{II}}_{t})=l_{i}\}$ for i=1,2,…,m, the above computation continues as

Denoting $\sum_{\Delta}=\sum_{k_{1}}\cdots\sum_{k_{n}}\sum_{l_{1}}\cdots\sum_{l_{m}}$, $q_{\Delta}=q_{k_{1}}\cdots q_{k_{n}}q_{l_{1}}\cdots q_{l_{m}}$, and $\Delta'=r\sum^{n}_{i=1}X^{I}_{i}+r\sum^{m}_{i=1}X^{\mathit{II}}_{i}$. Let k=k ₁+⋯+k _n , l=l ₁+⋯+l _m , we can write the above as

(A.18)

Since $I=\sum^{k}_{j=1}Y^{I}_{1j}$ is a sum of finite number of independent random variables with a common regular-tailed distribution, it follows from the closure properties of regular-tailed distribution family that I is still identically regular-tailed distributed; and so are $\mathit{II}=\sum^{l}_{j=1}Y^{\mathit{II}}_{1j}$. Furthermore, by the same property, the sum I+II also has the same regular-tailed distribution. However, the sum Δ′ is a random variable taking finite value. From the property of the regular-tailed distribution, (A.18) becomes the following as z→∞.

The above result can be written as follows:

Here $\sum_{k_{1}}k_{1}q_{k_{1}}=E[K^{I}_{1}(U^{I}_{t})],\dots,\sum_{k_{n}}k_{n}q_{k_{n}}=E[K^{I}_{n}(U^{I}_{t})]$, and $\sum_{l_{1}}l_{1}q_{l_{1}}=E[K^{\mathit{II}}_{1}(U^{\mathit{II}}_{t})],\allowbreak \dots,\sum_{l_{m}}l_{m}q_{l_{m}}=E[K^{\mathit{II}}_{m}(U^{\mathit{II}}_{t})]$.

(A.19)

Now, we can compute the probability Pr{Y(t)>z} in the same way and have

(A.20)

It follows from (A.19) and (A.20) that Lemma A.4 holds. □

Combining the results of Lemmas A.3 and A.4 with (A.19) and (A.20), we have, for a given t<∞,

This completes the proof of Theorem 5. □

Proof of Theorem 6

It is clear that Lemma A.3 is valid. Also, the result of (A.18) still holds under the conditions of Theorem 5. That is, for a given t,

as u→∞. Here the meanings of all symbols are the same as before.

However, using the current conditions, the sums $I=\sum_{j=1}^{k}Y_{1j}^{I}$ and $\mathit{II}=\sum_{j=1}^{l}Y_{1j}^{\mathit{II}}$ have regular-tailed distributions with the different indexes α and β, respectively. Since α<β, from the properties of regular-tailed distribution family, we know that I+II must be regular-tailed distributed and have the index α. Then, we repeat a procedure similar to the proof of Lemma A4 and have

(A.21)

and

(A.22)

Hence, the proof of Theorem 6 is completed by combining Lemma A.3, (A.21) and (A.22). □