Spatially explicit forest harvest scheduling with difference equations

Abstract

Spatially explicit harvest scheduling models optimize the layout of harvest treatments to best meet management objectives such as revenue maximization subject to a variety of economic and environmental constraints. A few exceptions aside, the mixed-integer programming core of every exact model in the literature requires one decision variable for every applicable prescription for a management unit. The only alternative to this “brute-force” method has been a network approach that tracks the management pathways of each unit over time via four sets of binary variables. Named after their linear programming-based aspatial predecessors, Models I and II, along with Model III, which has no spatial implementation, each of these models rely on static volume and revenue coefficients that must be calculated pre-optimization. We propose a fundamentally different approach that defines stand volumes and revenues as variables and uses difference equations and Boolean algebra to transition forest units from one planning period to the next. We show via three sets of computational experiments that the new model is a computationally promising alternative to Models I and II.

Appendices

Appendix A: Benchmark models

We present Model I, the first benchmark model, differently from existing literature in that we use a prescription-based rather than harvest timing-based formulation. The decision variables denote the choice whether a sequence of actions (e.g., harvests) should be applied to a management unit or not. Traditionally, integer versions of Model I have been presented with variables that represented “cut or not cut” decisions for each unit. The more general, prescription-based formulation was needed in our experiments because both Models II and IV allow any number of harvests to be applied to a given stand over a particular planning horizon. Among other things, one consequence of this generalization of Model I is that the prescription variables need to be mapped to harvest timing-based cluster variables for the Cluster Packing formulation to work (see Constraints (A.8)–(A.9)). Finally, our presentation of Model II is also new in that here, an ARM-based extension is used. Snyder and ReVelle’s (1996, 1997) Model II construct was URM-based.

1.1 A.1 Model I

To define the integer version of Johnson and Scheurman’s (1977) Model I, we let S denote the set of management units, t=1,2,…,T the time periods in the planning horizon, and k the minimum rotation age. We note that based on the assumption that harvests can occur only in the midpoints of the planning periods, the number of times a unit can potentially be harvested over the planning horizon is T/k. Model I requires the definition of the set of all possible prescriptions that can be assigned to a management unit: P={(0,…,0),(1,0,…,0),…}, where every prescription p∈P is a vector of length T. The elements of vector p represent the binary decisions of whether the management unit should be harvested in a particular planning period or not. The first element of the vector corresponds to period 1, the second to period 2, and so on. A value of one indicates that a harvest is to occur in the corresponding period, whereas zero indicates that no harvest should occur. Let 0–1 variable x _sp represent the decision whether unit s should follow prescription p. If it should, x _sp =1, 0 otherwise. Decision variables are created only for those prescriptions that would not lead to premature harvests. In other words, all prescription variables with first harvests that occur before the unit reaches its minimum rotation age are excluded from the model during pre-processing.

Further, for management unit s∈S, we let a _s denote the area, e _s the regeneration cost, and $v_{\mathit{sp}}^{t}$ the volume per unit area in period t given prescription p. We use h _t as an accounting variable for the volume harvested from the entire forest in period t, we use c for unit volume timber price, i for the real interest rate, and r _sp for the revenues associated with harvesting unit s according to prescription p. Finally, bounds f _min and f _max denote the allowable percent decrease and increase in harvest volume in consecutive planning periods. Such bounds are often used by practitioners to promote some level of operational sustainability. Then,

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)

defines the spatial version of Model I. The objective function (A.1) maximizes the net discounted timber revenues associated with the entire forest across the planning horizon of T periods with the revenue coefficients being

$$ r_{\mathit{sp}} = \sum_{t} \bigl( c \cdot a_{s} \cdot v_{\mathit{sp}}^{t} - e_{s} \bigr) \cdot ( 1 + i )^{ - t} ,\quad \forall s \in S,\ p \in P. $$

(A.7)

Constraint (A.2) ensures that each unit is assigned exactly one prescription. Constraint (A.3) calculates the harvest volume in each time period and Constraints (A.4) and (A.5) ensure that the harvest volume in adjacent planning periods does not fluctuate by more than a lower and an upper bound, f _min and f _max, respectively. Finally, Constraint (A.6) defines the decision variables as binary.

Model I can easily incorporate spatial constraints such as maximum or average harvest opening size restrictions. All of the three existing ARMs, McDill et al.’s (2002) Path, Goycoolea et al.’s (2005) Cluster Packing and Constantino et al.’s (2008) Bucket formulation, were introduced in the literature based on the Model I construct. Goycoolea et al.’s (2005) Cluster Packing is the only ARM, however, that can handle maximum average clear-cut size restrictions (Murray et al. 2004), which are often present in forest regulations. Cluster Packing requires an a priori enumeration of all contiguous clusters of management units whose combined area does not exceed the maximum allowable clear-cut size. Formally, a set of management units s∈θ that forms a connected sub-graph of graph G(S,E), where E denotes the edges representing the adjacency among the units (S), and for which inequality ∑ _s∈θ a _s ≤A _max (A _max = the maximum harvest opening size) holds, is called a feasible cluster. Let Θ denote the set of all feasible clusters that arise from a given problem instance. To incorporate Goycoolea et al.’s (2005) Cluster Packing approach in Model I, the management unit-based prescription variables x _sp ∈{0,1} must be mapped to cluster variables to account for the feasible clusters. Let u _θt ∈{0,1} denote the decision whether all management units in cluster θ should be cut in period t:

$$ \sum_{s \in \theta } \sum_{p \in P_{\theta t}} x_{\mathit{sp}} \ge| \theta| \cdot u_{\theta t},\quad \forall\theta\in \varTheta,\ t \le T; $$

(A.8)

$$ \sum_{s \in \theta } \sum_{p \in P_{\theta t}} x_{\mathit{sp}} - \sum_{s \in A_{\theta }} \sum _{p \in P_{\theta t}} x_{\mathit{sp}} - u_{\theta t} \le| \theta| - 1, \quad \forall\theta\in\varTheta,\ t \le T; $$

(A.9)

where P _θt is the set of all prescriptions applicable to cluster θ that involve a harvest in period t and A _θ is the set of management units that are adjacent to cluster θ. Constraint (A.8) allows, while Constraint (A.9) forces cluster θ to be “declared” cut in period t if all the units in the cluster, but none adjacent to it, are assigned prescriptions that involve a harvest in period t. To avoid double-counting the harvested areas, and to ensure that the maximum harvest opening size is never exceeded in any of the solutions, one constraint needs to written for each maximal clique of management units in each planning period. A set of mutually adjacent management units forms a maximal clique if no other unit exists that is adjacent to every member of the clique. Let K denote the set of all maximal cliques that arise from a problem with κ being one such clique. To prevent maximum harvest opening size violations, it is necessary that

$$ \sum_{\theta \in \varTheta _{\kappa }} u_{\theta t} \le 1, \quad \forall \kappa\in\mathrm{K} ,\ t \le T, $$

(A.10)

where Θ _κ is the set of feasible clusters that contain at least one management unit that is also a member of maximal clique κ. Constraint (A.10) requires that only one feasible cluster containing one or more units in clique κ is assigned to be clear-cut in period t. This precludes harvest arrangements where adjacent units are cut as parts of two or more feasible clusters of units whose combined area exceeds the maximum harvest opening size. Constraint (A.10), which is the multi-harvest version of the original Cluster Packing adjacency Constraint (Goycoolea et al. 2005), also prevents a unit from being part of multiple clusters in a given period. Finally, to enforce that the average harvest opening size over the entire planning horizon does not exceed $\bar{A}_{\max }$, we add the following forest-wide inequality (Murray et al. 2004):

$$ \sum_{\theta ,t} ( a_{\theta } - \bar{A}_{\max } ) \cdot u_{\theta t} \le 0 . $$

(A.11)

In Constraint (A.11), a _θ is the area of cluster θ and $\bar{A}_{\max }$ is the maximum allowable average clear-cut size.

If only maximum harvest opening size restrictions are present, McDill et al.’s (2002) Path Formulation can also be used by replacing (A.8)–(A.11) with the following set of adjacency constraints:

$$ \sum_{s \in C,\,p \in P_{\mathit{st}}} x{}_{\mathit{sp}} \le \vert C \vert - 1, \quad \forall C \in\varLambda^{ + },\ t \le T, $$

(A.12)

where P _st is the set of all prescriptions applicable to unit s that involve a harvest in period t. In the computational experiments, (A.1)–(A.7) were used for the Radiata problem, (A.1)–(A.11) for the Loblolly, and (A.1)–(A.7) and (A.12) for El Dorado.

1.2 A.2 Model II

To give a formal definition of Model II, we let variable sets b _st ,ℓ _st ∈{0,1} ∀s,t denote the decision whether unit s should be cut in period t the first time and whether it should be cut in period t the last time, respectively. If unit s is to be cut the first time in period t, then b _st =1, 0 otherwise. If unit s is to be cut the last time in period t, then ℓ _st =1, 0 otherwise. Further, we let variable set g _s,t′,t ∈{0,1} ∀s,t denote the decision whether unit s should be harvested in period t after it had last been cut in period t′. If it is, then g _s,t′,t =1, 0 otherwise. Lastly, we let n _s ∈{0,1} ∀s,t represent the “do-nothing” scenario. If unit s is not to be cut during the planning horizon, then n _s =1, 0 otherwise. Strictly speaking, variable set n _s ∈{0,1} is not needed for Model II except for the convenience of keeping track of uncut forest tracts.

As in Model I, we seek to maximize net timber revenues over the planning horizon subject to logical constraints that allow exactly one first harvest or no harvest of a unit, and harvest volume flow Constraints (A.16)–(A.18) that are analogous to inequalities (A.3)–(A.5) in Model I. We calculate the revenue coefficient associated with the first harvest of unit s in period t using relation $r_{\mathit{st}}^{b} = ( c \cdot a_{s} \cdot v_{\mathit{st}}^{b} - e_{s} ) \cdot( 1 + i )^{ - t}$, where $v_{\mathit{st}}^{b}$ is the harvest volume of unit s in period t given that this is the first time unit s is cut. Similarly, we use formula $r_{s,t',t}^{g} = ( c \cdot a_{s} \cdot v_{s,t',t}^{g} - e_{s} ) \cdot( 1 + i )^{ - t}$ to calculate the revenues associated with cutting unit s in period t after having cut it already in period t′. Parameter $v_{s,t',t}^{g}$ represents the unit area volume associated with the harvest of unit s in period t given that the previous harvest occurred in period t′. Then, the following function and set of inequalities define Model II:

(A.13)

(A.14)

(A.15)

(A.16)

(A.17)

(A.18)

(A.19)

(A.20)

(A.21)

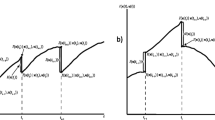
where Identity (A.15) is a “network flow” constraint that ensures whenever a management unit is cut in a particular period, whether it is the first, second or an intermediate harvest, there must be another variable that either declares this harvest to be the last for that unit or it forces it to be cut again during the planning horizon. In other words, this constraint forces each management unit to have a sound prescription plan with no discrepancies. Along with the logical Constraints (A.14), the flow constraints create a network representation of the harvest scheduling problem with nodes representing the starting (source), the ending (sink) and the intermediate states of the units (Fig. 1). Whatever harvest decision takes the unit to a given harvest-period state, there has to be another decision that moves it along to another state. This decision is either a declaration that this harvest was the unit’s last, or the unit could be cut again in a subsequent period. Finally, Constraints (A.19)–(A.21) define the four sets of decision variables as binary.

Model II is also compatible with all the three exact ARMs: McDill et al.’s (2002) Path, Goycoolea et al.’s (2005) Cluster Packing and Constantino et al.’s (2008) Bucket Formulation. Path constraints can be added as:

$$ \sum_{s \in C} \biggl( b_{\mathit{st}} + \sum_{t' \le t - k} g_{s,t',t} \biggr) \le \vert C \vert - 1, \quad \forall C \in\varLambda^{ + },\ t \le T. $$

(A.22)

Objective (A.13) and Constraints (A.14)–(A.22) were used to model the El Dorado problem with Model II in the computational experiment.

To incorporate Goycoolea et al.’s (2005) Cluster Packing Formulation, the decision variables in Model II are redefined to handle Cluster Packing. Variable sets b _st , ℓ _st , and g _s,t′,t are replaced with b _θt , ℓ _θt , and g _θ,t′,t to represent the decision whether cluster θ should be cut in period t first, whether it should be cut in period t last, and whether it should be cut in period t after it had already been cut in period t′, respectively. Variable b _θt takes the value of one if cluster θ is to be cut for the first time in period t,0 otherwise. Variable ℓ _θt takes the value of one if cluster θ is to be cut for the last time in period t, 0 otherwise. Lastly, g _θ,t′,t =1 if cluster θ is to be cut in period t after it had been cut in period t′, 0 otherwise. To incorporate harvest opening size restrictions using Goycoolea et al.’s (2005) model, objective function (A.13) and Constraints (A.14)–(A.21) remain the same except that all decision variables are replaced with the cluster variables as described above. To account for the logical condition that a given management unit can only be assigned to at most one feasible cluster that is cut in a particular period for the first time, we replace the logical constraint set (A.14) with

$$ n_{s} + \sum_{t,\theta :s \in \theta } b_{\theta t} = 1, \quad \forall s \in S. $$

(A.23)

Variable n _s is added to the sum of cluster assignments to account for the option of not cutting unit s during the planning horizon. We also replace the network flow constraints to allow a unit to be assigned to different clusters in each period:

$$ \sum_{\theta :s \in \theta } b_{\theta t} + \sum _{t' \le t - k,\theta :s \in \theta } g_{\theta ,t',t} = \sum_{t^* \ge t + k,\theta :s \in \theta } g_{\theta ,t,t^*} + \sum_{\theta :s \in \theta } \ell_{\theta t} , \quad \forall s \in S,\ t \le T. $$

(A.24)

To prevent adjacent management units from being assigned to multiple clusters that are cut at the same time, we add inequality set

$$ \sum_{\theta \in \varTheta _{\kappa }} \biggl( b_{\theta t} + \sum _{t' \le t - k} g_{\theta ,t',t} \biggr) \le 1, \quad \forall\kappa\in \mathrm{K} ,\ t \le T. $$

(A.25)

Constraints (A.25) are analogous to Constraints (A.10) in Model I; they ensure that maximum harvest opening size restrictions are never violated. Finally, to enforce the forest-wide maximum allowable average harvest opening size restriction ($\overline{A}_{\max }$), we require that:

$$ \sum_{\theta ,t} \biggl[ ( a_{\theta } - \bar{A}_{\max } ) \cdot\biggl( b_{\theta t} + \sum _{t' \le t - k} g_{\theta ,t',t} \biggr) \biggr] \le 0. $$

(A.26)

Appendix B: Goal programming to fit Model IV

We let ω _a denote the unit area volume of a management unit at age a (in periods) available from the original data, and we let $\omega_{a}^{*}$ denote the volume at age a coming from the logistic curve (1). For simplicity, we assume that the growth of each management unit is the same: volumes ω _a , accounting variables $\omega_{a}^{*}$ and the five parameters that are optimized for best fit have no s sub- or superscripts. This, of course, does not mean that Function (1) cannot be fitted for each management unit individually.

The objective of the GP, Function (A.1), minimizes the sum of absolute deviations, δ _a , between the fitted, $\omega_{a}^{*}$, and the original data, ω _a :

(B.1)

(B.2)

(B.3)

(B.4)

(B.5)

(B.6)

(B.7)

(B.8)

(B.9)

(B.10)

(B.11)

(B.12)

(B.13)

Constraints (B.2) and (B.3) calculate the absolute deviation, δ _a between $\omega_{a}^{*}$ and ω _a with the help of objective function (B.1), which maximizes the sum of the deviations. Constraint (B.4) sets the value of the fitted $\omega_{1}^{*}$ to be equal to ϕ _min. Constraints (B.5) and (B.6) work together to determine if the fitted volume at a particular age is above or below the inflection point β. If the volume is strictly above the inflection point, then y _a =1. Indicator y _a is zero otherwise. Note that the goal program will not allow the inflection point to be equal to the volume in any particular period, unless using the difference equation for the taper (B.9)–(B.10) vs. the exponential segment of the curve (B.7)–(B.8) does not make any difference in the objective function value. Recall that in the goal program, both the inflection point and the fitted volumes are variables. Constraints (B.5) through (B.10) establish the relationship between the five function parameters (ϕ _min, ϕ _max, γ _exp, γ _taper and β) that are to be optimized and the fitted volumes: $\omega_{a}^{*}\ \forall a \in A$. Along with inequalities (B.5)–(B.6), Constraints (B.7)–(B.10) capture Function (1). Lastly, Constraints, (B.11)–(B.13) define the domains of the variables.

While GP (B.1)–(B.13) is a quadratically constrained, non-convex,¹ and non-smooth² optimization problem, it is trivial to solve since it has only five decision variables (ϕ _min, ϕ _max, γ _exp, γ _taper and β) and only |A| accounting variables for the fitted volumes ($\omega_{a}^{*}$), the deviations (δ _a ) and the indicators y _a , each. Moreover, there is only one pair of goal constraints per data point, (B.2)–(B.3), and only a few extra constraints to account for the relationship between the volumes in consecutive age classes (B.4)–(B.10). GP (B.1)–(B.13) can be converted to a smooth optimization problem by optimizing for each binary combination of y _a ’s and selecting the combination that leads to the smallest total deviation. In this study, we used MS Excel Solver to fit Function (1).

Appendix C: Modeling intermediate treatments with Model IV

In this appendix, we discuss how Model IV can incorporate intermediate treatment decisions that are hard to capture in Models I and II parsimoniously: Should a management unit be thinned in a particular planning period with a given intensity or not? Should fertilization be applied to increase site productivity or should the trees be pruned? Thinning reduces the volume of the unit at the time of treatment and puts it on a steeper growth trajectory for merchantable timber. Thinings are applied in an attempt to maximize revenues or to improve forest health, or both. In addition to stimulating growth, fertilization can also increase site productivity, and pruning can change the quality of timber products.

The potential timings of treatments introduce additional prescriptions that are applicable to a management unit leading to an explosion of 0–1 variables in Model I. While the explosion is less dramatic in Model II, it is still an exponential function of the number of periods where intermediate treatments can occur. This is because additional sets of “first-”, “last-” and “intermediate harvest” variables are needed to link harvest decisions to intermediate treatments in prior or subsequent periods. If, in addition to the timing, the intensity of the treatments is also variable, then the combinatorial explosion is even more significant.

In Model IV, the number of extra decision variables that are needed to capture intermediate treatments increases only linearly as a function of the number of planning periods. To illustrate how Model IV can keep model size small, we consider a binary thinning decision τ _st in management unit s in period t with a preset thinning intensity of α∈[0,1]. Let variable τ _st take the value of one if unit s is to be thinned in period t, 0 otherwise. We assume that the expected post-thinning growth rates of the unit are known: $\gamma_{\exp '}^{s}$ in the exponential and $\gamma_{\mathrm{taper}'}^{s}$ in the taper section with an inflection point of β ^s. First, Constraints (6)–(9) in Model IV are modified so that they would inactivate should thinning occur in period t:

(C.1)

(C.2)

$$ v_{s,t + 1} - \phi_{\max }^{s}(y_{\mathit{st}} + \tau_{\mathit{st}}) \le\bigl( 1 + \gamma_{\exp }^{s} \bigr) \cdot v_{\mathit{st}},\quad \forall s \in S,\ t \le T - 1, $$

(C.3)

$$ v_{s,t + 1} + \phi_{\max }^{s}(y_{\mathit{st}} + x_{\mathit{st}} + \tau_{\mathit{st}}) \ge\bigl( 1 + \gamma_{\exp }^{s} \bigr) \cdot v_{\mathit{st}},\quad \forall s \in S,\ t \le T - 1. $$

(C.4)

If τ _st =1, the value of v _s,t+1 is unrestricted in inequalities (C.1)–(C.4) regardless of the value of indicator y _st because $v_{s,t + 1} \le\phi_{\max }^{s}$ and because $0 \le\gamma_{\mathrm{taper}}^{s} \le 1$. If τ _st =0, Constraints (C.1)–(C.4) work the same way as Constraints (6)–(9). To define the post-thinning growth of the units, we add:

$$ v_{s,t + 1} - \phi_{\max }^{s} \cdot( 1 + y_{\mathit{st}} - \tau_{\mathit{st}} ) \le\alpha\bigl( 1 + \gamma_{\exp '}^{s} \bigr) \cdot v_{\mathit{st}},\quad \forall s \in S,\ t \le T - 1; $$

(C.5)

$$ v_{s,t + 1} + \phi_{\max }^{s} \cdot ( 1 + y_{\mathit{st}} - \tau_{\mathit{st}} ) \ge\alpha \bigl( 1 + \gamma_{\exp '}^{s} \bigr) \cdot v_{\mathit{st}},\quad \forall s \in S,\ t \le T - 1; $$

(C.6)

(C.7)

(C.8)

These constraints are structurally similar to (6)–(9) or (C.1)–(C.4). The only difference is in the post-thinning growth rates. If τ _st =1, it is the value of y _st that determines whether the v _s,t+1 is going to be equal to the right-hand side of inequality (C.5)–(C.6) or (C.7)–(C.8). Note that the volume in period t is adjusted based on the intensity of thinning in period t:α. If τ _st =0, the value of v _s,t+1 becomes unrestricted regardless of the value of y _st . In this case, Constraints (C.1)–(C.4) become active and work the same way as the original Constraints (6)–(9).

The number of decision variables per unit that need to be introduced in Model IV to account for thinning decisions with set intensities is equal to the number of planning periods that are eligible for thinning. The number of extra constraints, Constraints (C.5)–(C.8), is four times the number of eligible periods. If the range of volumes that correspond to planning periods eligible for thinning falls exclusively below or above the inflection point, then either (C.5)–(C.6) or (C.7)–(C.8) may be dropped. Lastly, alternative thinning intensities, as well as fertilization and pruning decisions may be modeled the same way as thinning decisions. For fertilization and pruning, coefficient α will be one since no merchantable volume is removed from the unit. The post-treatment growth rates in volume (for fertilization) or revenues (for pruning) will drive the transition of the units from one period to the next in accordance with Constraints (C.5)–(C.8).