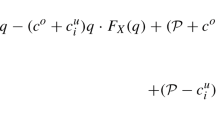Abstract
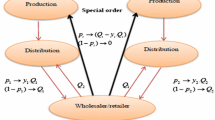
Multi-sourcing is considered as a common practice to hedge against supply disruption risk. In this context, this paper proposes two models for optimal order allocation in newsvendor setting, where both supply and demand are uncertain. The first model considers a risk neutral decision maker who maximizes the total expected profit under disruption risk. The second one is for a risk averse decision maker who does so under service level constraints. Analytical closed form solutions for both the models are derived. To overcome the computational complexity of the exact optimal solution, two algorithms are developed to generate optimal order quantity and the corresponding set of suppliers. The solutions with exact optimization algorithms and the proposed ones are illustrated and compared with numerical examples. The results show that the proposed algorithms give the exact optimal solution while being tractable. Finally, a case study is used to illustrate the applicability of the proposed model.





Similar content being viewed by others
Notes
Source: various reports from Government of Odisha,
http://www.dowrorissa.gov.in/HistoryofFLOOD/HistoryofFLOOD.pdf;
http://www.orissa.gov.in/disaster/src/ANNUAL_REP_04-05/Annual_Report_200910.pdf;
http://www.orissa.gov.in/disaster/src/ANNUAL_REP_04-05/ANNUAL_REPORT201112.pdf;
http://www.imd.gov.in/section/hydro/distrainfall/orissa.html
References
Agrawal, N., & Nahmias, S. (1997). Rationalization of the supplier base in the presence of yield uncertainty. Production and Operations Management, 6(3), 291–308.
Anupindi, R., & Akella, R. (1993). Diversification under supply uncertainty. Management Science, 39(8), 944–963.
Awasthi, A., Chauhan, S. S., Goyal, S. K., & Proth, J. M. (2009). Supplier selection problem for a single manufacturing unit under stochastic demand. International Journal of Production Economics, 117(1), 229–233.
Berger, P. D., Gerstenfeld, A., & Zeng, A. Z. (2004). How many suppliers are best? A decision-analysis approach. Omega, 32(1), 9–15.
Blackhurst, J., Craighead, C. W., Elkins, D., & Handfield, R. B. (2005). An empirically derived agenda of critical research issues for managing supply-chain disruptions. International Journal of Production Research, 43(19), 4067–4081.
Burke, G. J., & Vakharia, A. J. (2004). Supply chain management. The Internet Encyclopedia. New York: Wiley.
Burke, G. J., Carrillo, J. E., & Vakharia, A. J. (2007). Single versus multiple supplier sourcing strategies. European Journal of Operational Research, 182(1), 95–112.
Chaturvedi, A., & Martínez-de-Albéniz, V. (2011). Optimal procurement design in the presence of supply risk. Manufacturing & Service Operations Management, 13(2), 227–243.
Chopra, S., Reinhardt, G., & Mohan, U. (2007). The importance of decoupling recurrent and disruption risks in a supply chain. Naval Research Logistics (NRL), 54(5), 544–555.
Costantino, N., & Pellegrino, R. (2010). Choosing between single and multiple sourcing based on supplier default risk: A real options approach. Journal of Purchasing and Supply Management, 16(1), 27–40.
Chen, W., Feng, Q., & Seshadri, S. (2013). Sourcing from suppliers with random yield for price-dependent demand. Annals of Operations Research, 208(1), 557–579.
Christopher, M., & Lee, H. (2004). Mitigating supply chain risk through improved confidence. International Journal of Physical Distribution & Logistics Management, 34(5), 388–396.
Dada, M., Petruzzi, N. C., & Schwarz, L. B. (2007). A newsvendor’s procurement problem when suppliers are unreliable. Manufacturing & Service Operations Management, 9(1), 9–32.
Federgruen, A., & Yang, N. (2008). Selecting a portfolio of suppliers under demand and supply risks. Operations Research, 56(4), 916–936.
Federgruen, A., & Yang, N. (2009). Optimal supply diversification under general supply risks. Operations Research, 57(6), 1451–1468.
Gürler, Ü., & Parlar, M. (1997). An inventory problem with two randomly available suppliers. Operations Research, 45(6), 904–918.
Khouja, M. (1999). The single-period (news-vendor) problem: Literature review and suggestions for future research. Omega, 27(5), 537–553.
Kleindorfer, P. R., & Saad, G. H. (2005). Managing disruption risks in supply chains. Production and operations management, 14(1), 53–68.
Knemeyer, A. M., Zinn, W., & Eroglu, C. (2009). Proactive planning for catastrophic events in supply chains. Journal of Operations Management, 27(2), 141–153.
Minner, S. (2003). Multiple-supplier inventory models in supply chain management: A review. International Journal of Production Economics, 81, 265–279.
Meena, P. L., Sarmah, S. P., & Sarkar, A. (2011). Sourcing decisions under risks of catastrophic event disruptions. Transportation research part E: Logistics and transportation review, 47(6), 1058–1074.
Norrman, A., & Jansson, U. (2004). Ericsson’s proactive supply chain risk management approach after a serious sub-supplier accident. International Journal of Physical Distribution & Logistics Management, 34(5), 434–456.
Oke, A., & Gopalakrishnan, M. (2009). Managing disruptions in supply chains: A case study of a retail supply chain. International Journal of Production Economics, 118(1), 168–174.
Parlar, M., & Wang, D. (1993). Diversification under yield randomness in inventory models. European Journal of Operational Research, 66(1), 52–64.
Qin, Y., Wang, R., Vakharia, A. J., Chen, Y., & Seref, M. M. (2011). The newsvendor problem: Review and directions for future research. European Journal of Operational Research, 213(2), 361–374.
Ruiz-Torres, A. J., & Mahmoodi, F. (2007). The optimal number of suppliers considering the costs of individual supplier failures. Omega, 35(1), 104–115.
Sarkar, A., & Mohapatra, P. K. (2009). Determining the optimal size of supply base with the consideration of risks of supply disruptions. International Journal of Production Economics, 119(1), 122–135.
Sawik, T. (2011). Selection of supply portfolio under disruption risks. Omega, 39(2), 194–208.
Schmitt, A. J., & Snyder, L. V. (2012). Infinite-horizon models for inventory control under yield uncertainty and disruptions. Computers & Operations Research, 39(4), 850–862.
Silver, E., Pyke, D., & Peterson, R. (1998). Inventory management and production planning and scheduling. New York: Wiley.
Tang, C. S. (2006). Perspectives in supply chain risk management. International Journal of Production Economics, 103(2), 451–488.
Tang, C., & Tomlin, B. (2008). The power of flexibility for mitigating supply chain risks. International Journal of Production Economics, 116(1), 12–27.
Tomlin, B., & Wang, Y. (2005). On the value of mix flexibility and dual sourcing in unreliable newsvendor networks. Manufacturing & Service Operations Management, 7(1), 37–57.
Tomlin, B. (2006). On the value of mitigation and contingency strategies for managing supply chain disruption risks. Management Science, 52(5), 639–657.
Tomlin, B., & Wang, Y. (2012). The handbook of integrated risk management in global supply chains. Operational strategies for managing supply chain disruption risk (pp. 79–101). New York: Wiley.
Treleven, M., & Bergman Schweikhart, S. (1988). A risk/benefit analysis of sourcing strategies: Single vs. multiple sourcing. Journal of Operations Management, 7(3), 93–114.
Xanthopoulos, A., Vlachos, D., & Iakovou, E. (2012). Optimal newsvendor policies for dual-sourcing supply chains: A disruption risk management framework. Computers & Operations Research, 39(2), 350–357.
Yang, S., Yang, J., & Abdel-Malek, L. (2007). Sourcing with random yields and stochastic demand: A newsvendor approach. Computers & Operations Research, 34(12), 3682–3690.
Yang, G., & Qian, C. (2008). The optimal number of suppliers considering the quantity discount and supplier failure. In IEEE International Conference on Service Operations and Logistics, and Informatics, 2008. IEEE/SOLI 2008. (Vol. 2, pp. 2327–2329).
Yu, H., Zeng, A. Z., & Zhao, L. (2009). Single or dual sourcing: Decision-making in the presence of supply chain disruption risks. Omega, 37(4), 788–800.
Wu, D. D., Kefan, X., Gang, C., & Ping, G. (2010). A risk analysis model in concurrent engineering product development. Risk Analysis, 30(9), 1440–1453.
Wu, D., & Olson, D. L. (2008). Supply chain risk, simulation, and vendor selection. International Journal of Production Economics, 114(2), 646–655.
Wu, D. D., Olson, D. L., & Birge, J. R. (2011). Introduction to special issue on “Enterprise risk management in operations”. International Journal of Production Economics, 134(1), 1–2.
Wu, D., & Olson, D. L. (2010a). Enterprise risk management: Coping with model risk in a large bank. Journal of the Operational Research Society, 61(2), 179–190.
Wu, D. D., & Olson, D. (2010b). Enterprise risk management: A DEA VaR approach in vendor selection. International Journal of Production Research, 48(16), 4919–4932.
Wu, D., Wu, D. D., Zhang, Y., & Olson, D. L. (2013). Supply chain outsourcing risk using an integrated stochastic-fuzzy optimization approach. Information Sciences, 235, 242–258.
http://www.dowrorissa.gov.in/HistoryofFLOOD/HistoryofFLOOD.pdf. Accessed on 27th November, 2013.
http://www.orissa.gov.in/disaster/src/ANNUAL_REP_0405/Annual_Report_2009-10.pdf. Accessed on 27th November, 2013.
http://www.orissa.gov.in/disaster/src/ANNUAL_REP_0405/ANNUAL_REPORT2011-12.pdf. Accessed on 27th November, 2013.
http://www.imd.gov.in/section/hydro/distrainfall/orissa.html. Accessed on \(27^{{\rm th}}\) November, 2013.
http://en.wikipedia.org/wiki/1999_Odisha_cyclone. Accessed on \(24^{{\rm th}}\) November, 2013.
Acknowledgments
The authors would like to thank the editors and the anonymous reviewers for their constructive comments and suggestions, which have improved the quality and presentation of this paper. We would also like to thank all the resource persons, who have facilitated in our data collection.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix
Proof of Proposition 1
The expected profit function for two supplier case takes the following form:
Applying first order condition with respect to \(Q_{1}\) to the above equation, setting to zero and with further algebraic manipulation, we obtain the following equation.
This can be rewritten as;
Similar form will also be obtained, if the partial derivatives with respect to the other variables are considered. In general, for \(n\) variable problem, we can have \(n\) such equations of the following form:
The second order condition for two supplier case leads to a set of four equations each of which can be generalized in the following form:
where \(l_i =1\) if the function is first differentiated with respect to ith variable otherwise \(l_i =0;l_j =1\)if the function is first differentiated with respect to jth variable otherwise \(l_j =0;\)
For example when \(n=2\),
Please note that the above derivative is the product of \((-(s-r+k))\) which is always negative, and a positive term. All the elements of the Hessian matrix will be of this form. Therefore, the first order principal determinant of this matrix is in the following form.
The second order principal determinant is given by,
It may be noted that the second order determinant is the product of the square of a negative number (positive), and a positive term. Proceeding in this manner for specific cases of \(n\), it can be shown that the \(i{th}\) order principal determinant will have the form \(\left| {D_i } \right| =(-(s-r+k))^{i}\left[ {\hbox {a positive term}} \right] \), the sign of which will depend on the power ‘\(i\)’. Hence all the odd principal determinants are negative and the even ones are positive. Hence the function is proved to be negative definite and thus concave to the optimal order lot sizes.
Appendix 2
Proof of Proposition 2
For the model \((P_\beta )\) to be a convex programming problem in \(Q_1,Q_2 ,...,Q_n \), the objective function to be maximized should be concave and service constraint function should be convex. The objective function \(G_\beta \left( {Q_1 ,Q_2 ,...Q_n } \right) \) is proved to be concave in \(Q_1 ,Q_2 ,...,Q_n \) as above. For the convexity of the service level constraint, hessian matrix \(\nabla ^{2}G_\beta \left( {Q_1 ,Q_2 ,...,Q_n } \right) \) should be calculated.
The first order principal determinant is given by,
Continuing the arguments as the proof of Proposition 1 and with simple algebraic manipulation for a specific ‘\(n\)’ it can be shown that the higher order principal determinants will have the form which is always positive.
Hence, \(H\) is positive definite as its leading principal minors are positive. Therefore, function \(G_\beta \) is proved to positive definite and thus strictly convex. Thus, the model \(\left( {P_\beta } \right) \) is a convex programming problem. Corresponding Lagrangian relaxation problem as follows:
With
The solution of the first order conditions of the Lagrangian relaxation problem gives the global maximum value for problem \(LP_\beta \) and subsequently to the problem \(P_\beta \). The first order conditions of the above equation leads to Eqns 4 and 5.
Rights and permissions
About this article
Cite this article
Ray, P., Jenamani, M. Sourcing decision under disruption risk with supply and demand uncertainty: A newsvendor approach. Ann Oper Res 237, 237–262 (2016). https://doi.org/10.1007/s10479-014-1649-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-014-1649-8