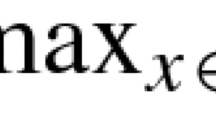Abstract
This study considers dynamic decisions of a retailer who seeks to determine the selling price and promotion expenditures associated with a perishable product, as well as to set the order quantity and the inter-replenishment time (cycle length). We propose an EOQ model in which the retailer faces a general demand function that is separable into multiplicative components of selling price, products’ age and promotion expenditure. We find analytical expressions for the optimal price and promotion trajectories; and we show that the former increases and the latter decreases in the products’ age, and that both are independent of the cycle length. Moreover, we show that the selling price is independent of the promotion expenditure, but not vice versa. It is also proved that under these optimal trajectories, the profit rate is strictly pseudo-concave in the cycle length. A comparison between dynamic and stationary strategies is given.


Similar content being viewed by others
References
Aust, G., & Buscher, U. (2012). Vertical cooperative advertising and pricing decisions in a manufacturer–retailer supply chain: A game-theoretic approach. European Journal of Operational Research, 223(2), 473–482.
Avinadav, T., & Arponen, T. (2009). An EOQ model for items with a fixed shelf-life and a declining demand rate based on time-to-expiry technical note. Asia-Pacific Journal of Operational Research, 26(06), 759–767.
Avinadav, T., Herbon, A., & Spiegel, U. (2013). Optimal inventory policy for a perishable item with demand function sensitive to price and time. International Journal of Production Economics, 144(2), 497–506.
Avinadav, T., Herbon, A., & Spiegel, U. (2014). Optimal ordering and pricing policy for demand functions that are separable into price and inventory age. International Journal of Production Economics, 155, 406–417.
Bakker, M., Riezebos, J., & Teunter, R. H. (2012). Review of inventory systems with deterioration since 2001. European Journal of Operational Research, 221(2), 275–284.
Bazaraa, M. S., Sherali, H. D., & Shetty, C. M. (2006). Nonlinear programming theory and application. New York: Wiley.
Cárdenas-Barrón, L. E., & Sana, S. S. (2014). A production-inventory model for a two-echelon supply chain when demand is dependent on sales teams’ initiatives. International Journal of Production Economics, 155, 249–258.
Costa, A. M., dos Santos, L. M. R., Alem, D. J., & Santos, R. H. (2014). Sustainable vegetable crop supply problem with perishable stocks. Annals of Operations Research, 219(1), 265–283.
De, S.K., & Sana, S.S. (2013). Backlogging EOQ model for promotional effort and selling price sensitive demand—An intuitionistic fuzzy approach. Annals of Operations Research, 1–20.
Diabat, A., Abdallah, T., & Le, T. (2014). A hybrid tabu search based heuristic for the periodic distribution inventory problem with perishable goods. Annals of Operations Research, 1–26.
Goyal, S. K., & Giri, B. C. (2001). Recent trends in modeling of deteriorating inventory. European Journal of Operational Research, 134(1), 1–16.
Goyal, S. K., & Gunasekaran, A. (1995). An integrated production-inventory-marketing model for deteriorating items. Computers & Industrial Engineering, 28(4), 755–762.
Hadley, G., & Whitin, T. M. (1963). Analysis of Inventory Systems. Englewood Cliffs, NJ: Prentice-Hall.
Herbon, A. (2014). Dynamic pricing vs. acquiring information on consumers’ heterogeneous sensitivity to product freshness. International Journal of Production Research, 52(3), 918–933.
Herbon, A., Levner, E., & Cheng, T. C. E. (2014). Perishable inventory management with dynamic pricing using time–temperature indicators linked to automatic detecting devices. International Journal of Production Economics, 147, 605–613.
Liu, G., Zhang, J., & Tang, W. (2014). Joint dynamic pricing and investment strategy for perishable foods with price-quality dependent demand. Annals of Operations Research, 1–20.
Maihami, R., & Nakhai Kamalabadi, I. (2012). Joint pricing and inventory control for non-instantaneous deteriorating items with partial backlogging and time and price dependent demand. International Journal of Production Economics, 136(1), 116–122.
Nahmias, S. (1982). Perishable inventory theory: A review. Operations Research, 30(4), 680–708.
Olsson, F. (2014). Analysis of inventory policies for perishable items with fixed leadtimes and lifetimes. Annals of Operations Research, 217(1), 399–423.
Rajan, A., Rakesh, & Steinberg, R. (1992). Dynamic pricing and ordering decisions by a monopolist. Management Science, 38(2), 240–262.
Sana, S. S. (2011a). An EOQ model for salesmen’s initiatives, stock and price sensitive demand of similar products—A dynamical system. Applied Mathematics and Computation, 218(7), 3277–3288.
Sana, S. S. (2011b). An EOQ model of homogeneous products while demand is salesmen’s initiatives and stock sensitive. Computers & Mathematics with Applications, 62(2), 577–587.
Sana, S. S. (2012). An economic order quantity model for nonconforming quality products. Service Science, 4(4), 331–348.
Sana, S. S. (2013). Sales team’s initiatives and stock sensitive demand—A production control policy. Economic Modelling, 31, 783–788.
Sana, S. S., & Panda, S. (2015). Optimal sales team’s initiatives and pricing of pharmaceutical products. International Journal of Systems Science: Operations & Logistics, 2(3), 168–176.
SeyedEsfahani, M. M., Biazaran, M., & Gharakhani, M. (2011). A game theoretic approach to coordinate pricing and vertical co-op advertising in manufacturer–retailer supply chains. European Journal of Operational Research, 211(2), 263–273.
Sheshinski, E., & Weiss, Y. (1977). Inflation and costs of price adjustment. The Review of Economic Studies, 287–303.
Soysal, G. P., & Krishnamurthi, L. (2012). Demand dynamics in the seasonal goods industry: An empirical analysis. Marketing Science, 31(2), 293–316.
Tsao, Y. C., & Sheen, G. J. (2008). Dynamic pricing, promotion and replenishment policies for a deteriorating item under permissible delay in payments. Computers & Operations Research, 35(11), 3562–3580.
Valliathal, M., & Uthayakumar, R. (2011). Optimal pricing and replenishment policies of an EOQ model for non-instantaneous deteriorating items with shortages. The International Journal of Advanced Manufacturing Technology, 54(1–4), 361–371.
Wei, Y., & Chen, Y. F. (2011). Joint determination of inventory replenishment and sales effort with uncertain market responses. International Journal of Production Economics, 134(2), 368–374.
Xie, J., & Wei, J. C. (2009). Coordinating advertising and pricing in a manufacturer–retailer channel. European Journal of Operational Research, 197(2), 785–791.
Yadavalli, V.S.S., Sundar, D.K., & Udayabaskaran, S. (2015). Two substitutable perishable product disaster inventory systems. Annals of Operations Research, 1–18.
Yang, C. T. (2014). An inventory model with both stock-dependent demand rate and stock-dependent holding cost rate. International Journal of Production Economics (in press).
Zhang, J. L., Chen, J., & Lee, C. Y. (2008). Joint optimization on pricing, promotion and inventory control with stochastic demand. International Journal of Production Economics, 116(2), 190–198.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
Proof of Lemma 4
Since \(\pi \left( {p(t),a(t),T} \right) =\Pi \left( {p(t),a(t),T} \right) /T\), then
By applying Leibniz’s rule to the profit function
we obtain
so the necessary condition for maximizing \(\pi (p(t),a(t),T)\) is
Hence, if \(\pi \left( {p^{*}(t),a^{*}(t),T^{*}} \right) >0\) then \(C(T^{*})<p(T^{*})\le p_{\max } \). \(\square \)
Appendix 2
Proof of Lemma 5
Differentiating Z(t) results in
Using algebraic manipulations and substituting Eq. (7), we obtain
By Eq. (6), \(r\left( {p^{*}(t)} \right) -C(t)=0\), so
By using the result of Corollary 1(ii), we obtain \(Z^{\prime }(t)<0\). \(\square \)
Rights and permissions
About this article
Cite this article
Avinadav, T., Chernonog, T., Lahav, Y. et al. Dynamic pricing and promotion expenditures in an EOQ model of perishable products. Ann Oper Res 248, 75–91 (2017). https://doi.org/10.1007/s10479-016-2216-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-016-2216-2