Integrated districting, fleet composition, and inventory planning for a multi-retailer distribution system

Abstract

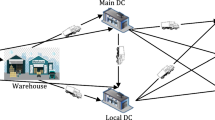
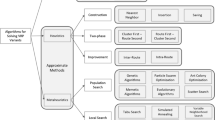
We study an integrated districting, fleet composition, and inventory planning problem for a multi-retailer distribution system. In particular, we analyze the districting decisions for a set of retailers such that the retailers within the same district share truck capacity for their shipment requirements. The number of trucks of each type dedicated to a retailer district and retailer inventory planning decisions are jointly determined in a district formation problem. We provide a mixed-integer-nonlinear programming formulation for this problem and develop a column generation based heuristic approach for its set partitioning formulation. To do so, we first characterize important properties of the optimal fleet composition and inventory planning decisions for a given retailer district. Then, we utilize these properties within a branch-and-price method to solve the integrated districting, fleet composition, and inventory planning problem. A set of numerical studies demonstrates the efficiency of the solution methods discussed for the investigated subproblems. An additional set of numerical studies compares the branch-and-price method to a commercial solver and an evolutionary heuristic method. Further numerical studies illustrate the economic as well as environmental benefits of the integrated modeling approach for various settings.

Appendix

1.1 Proof of Property 1

Suppose that $\sum _{k=1}^m p_k\widehat{z}_k^\mathbf{x }-\min _k\{p_k:\widehat{z}_k^\mathbf{x }\ge 1\}\ge \widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i$ and consider the following solution for P-x: $\widetilde{\mathbf{z }}^\mathbf{x }$, $\widehat{T}_\mathbf{x }$, and $\widehat{\mathbf{f }}^\mathbf{x }$ such that $\widetilde{z}_k^\mathbf{x }=\widehat{z}_k^\mathbf{x }$$\forall k: k\ne \min _k\{p_k:\widehat{z}_k^\mathbf{x }\ge 1\}$ and $\widetilde{z}_k^\mathbf{x }=\widehat{z}_k^\mathbf{x }-1$ for $k=\min _k\{p_k:\widehat{z}_k^\mathbf{x }\ge 1\}$. Then, one can observe that $\widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i\le \sum _{k=1}^m p_k\widetilde{z}_k^\mathbf{x }$, i.e., $\widetilde{\mathbf{z }}^\mathbf{x }$, $\widehat{T}_\mathbf{x }$, and $\widehat{\mathbf{f }}^\mathbf{x }$ define a feasible solution for P-x. Furthermore, it follows from Eq. (3) that $C_\mathbf{x }(\widetilde{\mathbf{z }}^\mathbf{x },\widehat{T}_\mathbf{x },\widehat{\mathbf{f }}^\mathbf x )< C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x },\widehat{T}_\mathbf{x },\widehat{\mathbf{f }}^\mathbf x )$, which contradicts that $\widehat{\mathbf{z }}^\mathbf{x },\widehat{T}_\mathbf{x },\widehat{\mathbf{f }}^\mathbf x$ is an optimal solution of P-x. $\square$

1.2 Summary of the notation used

Notation	Description	Metric
Indices
i	Index for retailers	$i=1,2,\ldots ,n$
j	Index for districts	$j=1,2,\ldots ,n$
k	Index for truck types	$k=1,2,\ldots ,m$
Retailer parameters
$h_i$	Holding cost of retailer i per unit per unit time	$/unit/time
$b_i$	Backordering cost of retailer i per unit per unit time	$/unit/time
$a_i$	Fixed order cost of retailer i	$/order
$\lambda _i$	Demand rate of retailer i	Units/time,
Truck parameters
$r_k$	Shipment cost of a type k truck	$
$p_k$	Shipment capacity of a type k truck	Units
Decision variables
$t_i$	Retailer i’s replenishment cycle length	Time
$f_i$	Retailer i’s fill rate
$x_{ij}$	1 if retailer i belongs to district j, 0 otherwise	Binary
$z^j_k$	Number of type k trucks in district j’s fleet composition	Integer
$T_j$	Common replenishment cycle length for district j	Time

1.3 Proof of Property 2

First note that for any given $\mathbf z ^\mathbf{x }$ and $T_\mathbf{x }$, $f_i^0=\frac{b_i}{b_i+h_i}$$\forall i\in S_\mathbf{x }$ minimizes $C_\mathbf{x }(\mathbf z ^\mathbf{x },T_\mathbf{x },\mathbf f ^\mathbf x )$, i.e., $\widehat{\mathbf{f }}^\mathbf x =\mathbf f ^0$. Let $C_\mathbf{x }(\mathbf z ^\mathbf{x },T_\mathbf{x },\mathbf f ^0)=\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)+\varOmega _\mathbf{x }(\mathbf z ^\mathbf{x },T_\mathbf{x })$, where $\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)=\frac{T_\mathbf{x }}{2}\left( \sum _{i\in S_\mathbf{x }}\lambda _i[h_i(f_i^0)^2+b_i(1-f_i^0)^2]\right) +\frac{\sum _{i\in S_\mathbf{x }}a_i}{T_\mathbf{x }}$ and $\varOmega _\mathbf{x }(\mathbf z ^\mathbf{x },T_\mathbf{x })=\frac{\sum _{k=1}^mr_kz_k^\mathbf{x }}{T_\mathbf{x }}$.

Lemma 1

$\Pi _\mathbf{x }(T^L_\mathbf{x },\mathbf f ^0)<\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)$ for $T_\mathbf{x }<T^L_\mathbf{x }$ and $\Pi _\mathbf{x }(T^U_\mathbf{x },\mathbf f ^0)<\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)$ for $T_\mathbf{x }>T^U_\mathbf{x }$.

Proof

It can be shown that $\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)$ is a strictly convex function of $T_\mathbf{x }$ and $T_\mathbf{x }^0=\sqrt{ \frac{2\sum _{i\in S_\mathbf{x }}a_i }{\sum _{i\in S_\mathbf{x }}\lambda _i\left( \frac{h_ib_i}{h_i+b_i}\right) }}$ minimizes $\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)$. Furthermore, note that

$$\begin{aligned} T^L_\mathbf{x }=\frac{p_{k^*}}{\sum _{i\in S_\mathbf{x }}\lambda _i}\left\lfloor \frac{\sum _{i\in S_\mathbf{x }}\lambda _i}{p_{k^*}} T_\mathbf{x }^0 \right\rfloor \le T_\mathbf{x }^0\ \ and\ \ T^U_\mathbf{x }=\frac{p_{k^*}}{\sum _{i\in S_\mathbf{x }}\lambda _i}\left\lceil \frac{\sum _{i\in S_\mathbf{x }}\lambda _i}{p_{k^*}} T_\mathbf{x }^0 \right\rceil \ge T_\mathbf{x }^0. \end{aligned}$$

The result then follows from the convexity of $\Pi _\mathbf{x }(T_\mathbf{x },\mathbf f ^0)$ with respect to $T_\mathbf{x }$. $\square$

Lemma 2

Given $t>0$, let $\widehat{\mathbf{z }}^\mathbf{x |t}$ be an optimal solution of P-x|t, where

Then $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x | T^L_\mathbf{x }},T^L_\mathbf{x })=\varOmega _\mathbf{x } (\widehat{\mathbf{z }}^\mathbf{x |T^U_\mathbf{x }},T^U_\mathbf{x }) =\frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$.

Proof

We first prove that $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x | T^U_\mathbf{x }},T^U_\mathbf{x })=\frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$. Consider the linear relaxation of P-x|t:

and let $\overline{\mathbf{z }}^\mathbf{x |t}$ be an optimal solution of LR-P-x|t. Note that $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |t},t)\ge \varOmega _\mathbf{x }(\overline{\mathbf{z }}^\mathbf{x |t},t)$ by definition. Letting $\beta$ be the dual variable associated with the single constraint in LR-P-x|t, one can note that the dual of LR-P-x|t is:

One can easily observe that the optimal solution (and optimum objective function value) of D-LR-P-x|t is $\min _{k}\{r_k/p_k\}\sum _{i\in S_\mathbf{x }}\lambda _i=\frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$. Therefore, we have $\varOmega _\mathbf{x }(\overline{\mathbf{z }}^\mathbf{x |t},t)= \frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$, which implies that $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |t},t)\ge \frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$ for any given $t>0$.

Now, let $t=T^L_\mathbf{x }$ and let us define $\overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}$ such that $\overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}_{k^*} =\frac{T^L_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i }{p_{k^*}}$ and $\overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}_{k}=0$$\forall k\ne k^*$. It then follows that $\varOmega _\mathbf{x }(\overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }},T^L_\mathbf{x })=\frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$. That is, $\overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}$ is indeed the optimal solution of LR-P-x$|T^L_\mathbf{x }$. Furthermore, note that $\overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}$ is an integer vector; hence, it is feasible for P-x$|T^L_\mathbf{x }$. Therefore, $\widehat{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}= \overline{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }}$ and $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x | T^L_\mathbf{x }},T^L_\mathbf{x })=\frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$. Similarly, it can be shown that $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x | T^U_\mathbf{x }},T^U_\mathbf{x })=\frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i$. $\square$

Note that $C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x },\widehat{T}_\mathbf{x },\widehat{\mathbf{f }}_\mathbf{x }) =C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |\widehat{T}_\mathbf{x }},\widehat{T}_\mathbf{x },\mathbf f ^0) =\Pi _\mathbf{x }(\widehat{T}_\mathbf{x },\mathbf f ^0)+\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |\widehat{T}_\mathbf{x }},\widehat{T}_\mathbf{x })$. Now suppose that $\widehat{T}_\mathbf{x }<T^L_\mathbf{x }$. It then follows from Lemma 1 that $\Pi _\mathbf{x }(T^L_\mathbf{x },\mathbf f ^0)<\Pi _\mathbf{x }(\widehat{T}_\mathbf{x },\mathbf f ^0)$. Furthermore, we know that $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |\widehat{T}_\mathbf{x }},\widehat{T}_\mathbf{x })\ge \frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i = \varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }},T^L_\mathbf{x })$ (see the proof of Lemma 2). Therefore, we have $C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x },\widehat{T}_\mathbf{x },\widehat{\mathbf{f }}_\mathbf{x })> C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |T^L_\mathbf{x }},T^L_\mathbf{x },\mathbf f ^0)$, which is a contradiction that $\widehat{T}_\mathbf{x }$ is optimum to P-x. Similarly, suppose that $\widehat{T}_\mathbf{x }>T^U_\mathbf{x }$. It then follows from Lemma 1 that $\Pi _\mathbf{x }(T^U_\mathbf{x },\mathbf f ^0)<\Pi _\mathbf{x }(\widehat{T}_\mathbf{x },\mathbf f ^0)$. Furthermore, from the proof of Lemma 2, we know that $\varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |\widehat{T}_\mathbf{x }},\widehat{T}_\mathbf{x })\ge \frac{r_{k^*}}{p_{k^*}}\sum _{i\in S_\mathbf{x }}\lambda _i = \varOmega _\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |T^U_\mathbf{x }},T^U_\mathbf{x })$. Therefore, we have $C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x },\widehat{T}_\mathbf{x },\widehat{\mathbf{f }}_\mathbf{x })> C_\mathbf{x }(\widehat{\mathbf{z }}^\mathbf{x |T^U_\mathbf{x }},T^U_\mathbf{x },\mathbf f ^0)$, which is a contradiction that $\widehat{T}_\mathbf{x }$ is optimum to P-x. $\square$

1.4 Proof of Property 3

We first prove that $\varUpsilon ^L_\mathbf{x }\le \sum _{k=1}^m\widehat{z}_k^\mathbf{x }$ by contradiction. First of all, it follows from Eq. (6) that $\varUpsilon ^L_\mathbf{x }\le \frac{T^L_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i}{\max _k\{p_k\}}$. Furthermore, we know from Property 2 that $T^L_\mathbf{x }\le \widehat{T}_\mathbf{x }$. It then follows that $\varUpsilon ^L_\mathbf{x }\le \widehat{T}_\mathbf{x } \frac{\sum _{i\in S_\mathbf{x }}\lambda _i}{\max _k\{p_k\}}$, which implies that (i) $(\varUpsilon ^L_\mathbf{x }-1)\max _k\{p_k\}< \widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i$. To get a contradiction, suppose that $\sum _{k=1}^m\widehat{z}_k^\mathbf{x }\le \varUpsilon ^L_\mathbf{x }-1$. It then follows that $\sum _{k=1}^m p_k\widehat{z}_k^\mathbf{x }\le (\varUpsilon ^L_\mathbf{x }-1)\max _k\{p_k\}$. Considering inequality (i), we then have (ii) $\sum _{k=1}^m p_k\widehat{z}_k^\mathbf{x }<\widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i$. Inequality (ii) contradicts Property 1; therefore, one should have $\varUpsilon ^L_\mathbf{x }\le \sum _{k=1}^m\widehat{z}_k^\mathbf{x }$.

Next, we prove that $\sum _{k=1}^m\widehat{z}_k^\mathbf{x }\le \varUpsilon ^U_\mathbf{x }$ by contradiction. First of all, it follows from Eq. (7) that $\varUpsilon ^U_\mathbf{x }\ge \frac{T^U_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i}{\min _k\{p_k\}}$. Furthermore, we know from Property 2 that $\widehat{T}_\mathbf{x }\le T^U_\mathbf{x }$. It then follows that (iii) $\varUpsilon ^U_\mathbf{x }\min _k\{p_k\} \ge \widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i$. To get a contradiction, suppose that $\sum _{k=1}^m\widehat{z}_k^\mathbf{x }\ge \varUpsilon ^U_\mathbf{x }+1$. It then follows that $\sum _{k=1}^m p_k\widehat{z}_k^\mathbf{x }\ge \varUpsilon ^U_\mathbf{x }\min _k\{p_k\}+\min _k\{p_k:\widehat{z}_k^\mathbf{x }\ge 1\}$. Considering inequality (iii), we then have (iv) $\sum _{k=1}^m p_k\widehat{z}_k^\mathbf{x }\ge \widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i +\min _k\{p_k:\widehat{z}_k^\mathbf{x }\ge 1\}$. Inequality (iv) implies that $\sum _{k=1}^m p_k\widehat{z}_k^\mathbf{x }-\min _k\{p_k:\widehat{z}_k^\mathbf{x }\ge 1\}\ge \widehat{T}_\mathbf{x }\sum _{i\in S_\mathbf{x }}\lambda _i$, which contradicts Property 1; therefore, one should have $\sum _{k=1}^m\widehat{z}_k^\mathbf{x }\le \varUpsilon ^U_\mathbf{x }$. $\square$

1.5 Proof of Property 4

First note that Eq. (10) can be written as follows:

$$\begin{aligned} G(\widetilde{\mathbf{x }},\widetilde{\mathbf{z }},\widetilde{T},\mathbf f )= \sum _{i=1}^n\widetilde{x}_i\left( \frac{\widetilde{T}}{2} \lambda _i\left[ h_if_i^2+b_i(1-f_i)^2\right] +\frac{1}{\widetilde{T}}a_i -\pi _i \right) +\frac{1}{\widetilde{T}}\sum _{k=1}^mr_k\widetilde{z}_k, \end{aligned}$$

where the second term is a positive value. Furthermore, note that $\widetilde{f}_i^*=\frac{b_i}{b_i+h_i}$. Let $\alpha _i(\widetilde{T})=\frac{\widetilde{T}}{2}\lambda _i[h_if_i^2+b_i(1-f_i)^2]+\frac{1}{\widetilde{T}}a_i -\pi _i$. One can then observe that if $\alpha _i(\widetilde{T}^*)\ge 0$, then $\widetilde{x}^*_i=0$ since we want to minimize $G(\widetilde{\mathbf{x }},\widetilde{\mathbf{z }},\widetilde{T},\mathbf f )$. It can be remarked that $\alpha _i(\widetilde{T})$ is a quadratic convex function of $\widetilde{T}$, and it follows from the quadratic equation that $\alpha _i(\widetilde{T})<0$ when $\tau _i^L<\widetilde{T}<\tau _i^U$, where $\tau _i^L$ and $\tau _i^U$ are defined in Eqs. (11) and (12), respectively. Therefore, $\widetilde{x}^*_i=0$ if $\widetilde{T}^*\notin (\tau _i^L,\tau _i^U)$. $\square$

1.6 Proof of Property 5

Noting that $\widetilde{f}_i^{\widetilde{T}}=\frac{b_i}{b_i+h_i}$$\forall i$, LR-PP-$\widetilde{T}$ is equal to

where $\alpha _i=\lambda _i h_i b_i \widetilde{T}/2(h_i+b_i)+a_i/\widetilde{T}-\pi _i$, $\widehat{r}_k=r_k/\widetilde{T}>0$, and $\beta _i=\lambda _i \widetilde{T}>0$. One can easily note that $\sum _{i=1}^n \beta _i\widetilde{x}_i=\sum _{k=1}^mp_k\widetilde{z}_k$ in the solution of LR-PP-$\widetilde{T}$ since $\widehat{r}_k>0$ and $\beta _i>0$. This indicates that $\widetilde{x}_i^{\widetilde{T}}=0$ if $\alpha _i\ge 0$.

Now, without loss of generality, suppose that $\alpha _i< 0$$\forall i$ and let us consider the dual of LR-PP-$\widetilde{T}$

where $\phi$ is the dual variable associated with the first constraint of LR-PP-$\widetilde{T}$ and $w_i$ is the dual variable associated with $\widetilde{x}_i\le 1$ constraint. Note that $\max \left\{ \sum _{i=1}^nw_i:\mathbf w \le \mathbf 0 \right\} \le 0$. Thus, $w_i=0$$\forall i$ and $0\ge \phi \ge max\{-\widehat{r}_k/p_k\}$ is an optimal solution to D-LR-PP-$\widetilde{T}$. It then follows that there is a dual optimal solution such that $\beta _i \phi +w_i< \alpha _i\ \forall i$, which implies that $\widetilde{x}_i=1$ in the optimal primal solution from complementary slackness. Therefore, $\widetilde{x}_i^{\widetilde{T}}=1$ if $\alpha _i< 0$. $\square$