Optimal recovery strategy of manufacturers: Remanufacturing products or recycling materials?

Abstract

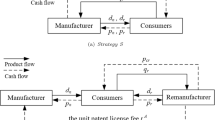
Manufacturers are increasingly taking positive actions to handle used products by adopting “recycling materials” (RM), “remanufacturing product” (RP) or the hybrid strategy combining with both RM and RP (RMP). Under each strategy, in addition to the optimal quantity and price of new product, manufacturers may also face important decisions on the optimal quantity and price of remanufactured product and (or) recycling materials. To address such challenging issues, we consider a manufacturer who sells a new product to consumers, and examine the optimal recovery strategy and associated decisions by developing three models, i.e., models without incorporating recovery strategy, with considering recovery strategy and both recovery strategy and government subsidy. We further explore the impacts of product quality and government subsidy on the optimal decisions. Our results show that, neither recovery strategy including not implementing recovery strategy is always superior to the others, which depends on cost savings from remanufacturing products and benefits of recycling materials. Interestingly, the manufacturer with a higher product quality prefers to choose RP but RM otherwise. Government subsidy increases the manufacturer’s profit under each recovery strategy. In general, government subsidy helps to increase consumer surplus but reduce environment impact. However, as government subsidy increases, the manufacturer may prefer to implement RMP rather than RP, which may result in less consumer surplus and more environmental impact. Therefore, a higher subsidy unexpectedly may lead to a lower social welfare. This suggests that, the government should design an appropriate and more practical subsidy policy to dispose used products.

Appendix

1.1 Proof of Theorem 1

It can be verified that $\Pi^{R}$ is strictly concave in $q_{n}^{R}$, $q_{r}^{R}$, and $q_{d}^{R}$. The Lagrangian and the Karush–Kuhn–Tucker optimality conditions of model R are:

$$ \begin{aligned} L\left( {q_{n}^{R} ,q_{r}^{R} ,q_{d}^{R} } \right) & = t\left( {Q - q_{n}^{R} - \alpha q_{r}^{R} } \right)q_{n}^{R} + \alpha t\left( {Q - q_{n}^{R} - q_{r}^{R} } \right)q_{r}^{R} + bq_{d}^{R} - ct^{2} q_{n}^{R} \\ & \quad - (c - \Delta )t^{2} q_{n}^{R}- \;\beta \left( {q_{d}^{R} + q_{r}^{R} } \right)^{2} + \lambda_{1} \left( {q_{n}^{R} - q_{d}^{R} - q_{r}^{R} } \right) + \lambda_{2} q_{r}^{R} + \lambda_{3} q_{d}^{R} \\ \end{aligned} $$

$$ \frac{\partial L}{{\partial q_{n}^{R} }} = \lambda_{1} - t\left( {2q_{n}^{R} + 2\alpha q_{r}^{R} + ct - Q} \right) = 0 $$

(A.1)

$$ \frac{\partial L}{{\partial q_{r}^{R} }} = \lambda_{2} - \lambda_{1} + t\left( {\alpha Q - t(c - \Delta ) - 2\alpha \left( {q_{r}^{R} + q_{n}^{R} } \right)} \right) - 2\beta \left( {q_{r}^{R} + q_{d}^{R} } \right) = 0 $$

(A.2)

$$ \frac{\partial L}{{\partial q_{d}^{R} }} = \lambda_{3} - \lambda_{1} + b - 2\beta \left( {q_{r}^{R} + q_{d}^{R} } \right) = 0 $$

(A.3)

$$ \lambda_{1} \left( {q_{n}^{R} - q_{d}^{R} - q_{r}^{R} } \right) = 0 $$

(A.4)

$$ \lambda_{2} q_{r}^{R} = 0 $$

(A.5)

$$ \lambda_{3} q_{d}^{R} = 0 $$

(A.6)

According to the Karush–Kuhn–Tucker condition method, we can derive four optimal strategies, which are characterized as follows.

Case NR ($\lambda_{1} = 0$, $\lambda_{2} > 0$, and $\lambda_{3} > 0$):

When $\lambda_{2} > 0$, and $\lambda_{3} > 0$, we can have $q_{r}^{R} = 0$, and $q_{d}^{R} = 0$, respectively. Therefore, from Eq. (A.1), we can obtain

$$ q_{n}^{R*} = \frac{1}{2}(Q - ct),\quad q_{r}^{R*} = 0,\quad q_{d}^{R*} = 0,\quad {\text{and}}\quad \lambda_{2} = t^{2} (c(1 - \alpha ) - \Delta ),\quad \lambda_{3} = b. $$

(A.7)

Substituting them into the linear inverse demand functions in model R, we have:

$$ p_{n}^{R*} = \frac{1}{2}t(Q + ct),\quad {\text{and}}\quad p_{r}^{R*} = \frac{t\alpha (Q + ct)}{2}. $$

The values of $\lambda_{2}$ and $\lambda_{3}$ must be positive, and the first constraint of model R must be nonnegative, leading to the necessary condition in this case: $\Delta < c(1 - \alpha ).$

Case RM ($\lambda_{1} = 0$, $\lambda_{2} > 0$, and $\lambda_{3} = 0$):

$$ {\text{When}}\;\lambda_{2} > 0,\;{\text{we}}\;{\text{have}}\;q_{r}^{R} = 0. $$

(A.8)

Based on Eqs. (A.1)–(A.3) and (A.7), we can derive:

$$ q_{n}^{R*} = \frac{1}{2}(Q - ct),\quad q_{r}^{R*} = 0,\quad q_{d}^{R*} = b/2\beta ,\quad {\text{and}}\quad \lambda_{2} = b - t^{2} (\Delta - c(1 - \alpha )). $$

Substituting them into the linear inverse demand functions in model R, we obtain:

$$ p_{n}^{R*} = \frac{1}{2}t(Q + ct),\quad {\text{and}}\quad p_{r}^{R*} = \frac{t\alpha (Q + ct)}{2}. $$

The value of $\lambda_{2}$ must be positive, and the first and third constraints of model R must be nonnegative, which leads to the necessary condition in this case: $c(1 - \alpha ) \le \Delta < \frac{b}{{t^{2} }} + c(1 - \alpha ).$

Case RMP ($\lambda_{1} = 0$, $\lambda_{2} = 0$, and $\lambda_{3} = 0$):

From Eqs. (A.1)–(A.3), we can obtain: $q_{n}^{R*} = \frac{{b + Qt(1 - \alpha ) - t^{2} \Delta }}{2t(1 - \alpha )}$, $q_{d}^{R*} = \frac{b\beta + t((1 - \alpha )(ct\beta + b) - t\beta \Delta )}{2t(1 - \alpha )\alpha \beta }\quad {\text{and}}\quad q_{r}^{R*} = \frac{{t^{2} (\Delta - c(1 - \alpha )) - b}}{2t(1 - \alpha )\alpha }.$

Substituting optimal prices into the linear inverse demand functions in model R, we have:

$$ p_{n}^{R*} = \frac{1}{2}t(Q + ct),\quad {\text{and}}\quad p_{r}^{R*} = \frac{1}{2}(b + t(ct + Q\alpha - t\Delta )). $$

In this case, the constraints in model R must be nonnegative; thus, the necessary condition for this case is: $\frac{b}{{t^{2} }} + c(1 - \alpha ) \le \Delta < \frac{{b\alpha (1 - \alpha ) + (b + ct^{2} (1 - \alpha ))\beta }}{{\beta t^{2} }}.$.

Case RP ($\lambda_{1} = 0$, $\lambda_{2} = 0$, and $\lambda_{3} > 0$):

$$ {\text{When}}\;\lambda_{3} > 0\;{\text{we}}\;{\text{have}}:\;q_{d}^{R} = 0. $$

(A.9)

From Eqs. (A.1)–(A.3) and (A.8), we can obtain:

$$ \begin{aligned} q_{n}^{{R*}} &= \frac{{Q(t(1 - \alpha )\alpha + \beta ) - t(c\beta + t\alpha \Delta )}}{{2t(1 - \alpha )\alpha + 2\beta }},\quad q_{r}^{{R*}} = \frac{{t^{2} (c(1 - \alpha ) - \Delta )}}{{2t(1 - \alpha )\alpha + 2\beta }},\quad q_{d}^{{R*}} = 0,\quad {\text{and}} \\ {\lambda _{3}} & = \frac{{\beta (t^{2} (\Delta - c(1 - \alpha ))}}{{t(1 - \alpha ) + \beta }} - b.\end{aligned}$$

Substituting optimal prices into the linear inverse demand functions in model R, we have:

$$ p_{n}^{R*} = \frac{1}{2}t(Q + ct),\quad {\text{and}}\quad p_{r}^{R*} = \frac{{t\alpha ((1 - \alpha )(ct^{2} + Q - \Delta t) + (Q + ct)\beta ).}}{2t(1 - \alpha )\alpha + 2\beta } $$

The value of $\lambda_{3}$ must be positive, and the first and second constraints of model R must be nonnegative, leading to the necessary condition in this case $\Delta \ge \frac{{b\alpha (1 - \alpha ) + (b + ct^{2} (1 - \alpha ))\beta }}{{\beta t^{2} }}.$

The proof of model RS is similar to that of model R, and thus omitted here. We provide optimal decisions and outcomes of models R and RS in Tables 2 and 3, respectively. □

1.2 Proof of Corollary 1

We explore the monotonicity of threshold interval lengths by using partial differentiation techniques. For example, taking the first-order partial derivatives of $\bar{\Delta }_{2} - \bar{\Delta }_{1}$ with respect to $t$, we have $\frac{{\partial (\bar{\Delta }_{2} - \bar{\Delta }_{1} )}}{\partial t} = - \frac{2b}{{t^{3} }}$. Therefore, $\bar{\Delta }_{2} - \bar{\Delta }_{1}$ decreases with $t$. All the first-order partial derivatives of threshold interval lengths are given in Table 4. According to these results of first-order partial derivatives, we can reach the findings in Corollary 1. □

Table 4 The first-order partial derivatives of threshold interval lengths

1.3 Proof of Proposition 2

We use partial differentiation techniques to examine the sensitivities of optimal solutions to product quality level $t$. The proof is similar to the proof of Corollary 1, and thus omitted here. □

1.4 Proof of Corollary 2

Substituting optimal solutions under strategy NR into the profit function in model R, we have $\Pi^{NR} = \frac{{(Q - ct)^{2} t}}{4}$. It can be verified that $\Pi^{NR}$ is strictly concave in $t$. By solving the first-order condition $\frac{{\partial \Pi^{NR} }}{\partial t} = 0$, we can have the optimal product quality level is $\bar{t}_{NR}^{*} = Q/3c$. Similarly, we can derive the optimal product quality level under strategy RM is $\bar{t}_{RM}^{*} = Q/3c.$

Substituting optimal solutions under strategy RMP into the profit function in model R, we have

$$ \begin{aligned} \Pi^{R} & = \frac{1}{4t(1 - \alpha )\alpha \beta }\left( {b^{2} (t(1 - \alpha )\alpha + \beta ) + t(1 - \alpha )\left( {c^{2} t^{3} \beta + \alpha (Qt(Q - 2ct)\beta )} \right)} \right. \\ & \quad \left. { - 2ct^{4} ((1 - \alpha )\beta \Delta + t^{4} \beta \Delta^{2} + 2bt((1 - \alpha )ct\beta + t\beta \Delta ))} \right). \\ \end{aligned} $$

It can be verified that $\Pi^{R}$ is strictly concave in $t$, because $\frac{{\partial^{2} \Pi^{R} }}{{\partial t^{2} }} > 0$. Taking the first-order partial derivatives of $\Pi^{R}$ with respect to $t$, we can have $\frac{{\partial \Pi^{R} }}{\partial t} = \frac{Q\alpha (Q - 2ct)}{4} + \frac{R}{{4\alpha t^{2} (1 - \alpha )}}$, where $R = 3t^{4} (1 - \alpha )((2c - 1)\Delta + (1 - \alpha )c^{2} ) + b(2t^{2} (\Delta - c(1 - \alpha )) + b) > 0$. Therefore, we have $\bar{t}_{RMP} > \frac{Q}{2c} > \bar{t}_{RM} = \bar{t}_{NR}$. Similarly, we can have $\frac{{\partial \Pi^{R} }}{\partial t} = Q(Q - 2ct) + \frac{T}{{4(\alpha t(1 - \alpha ) + \beta )^{3} }}$, where

$$ \begin{aligned} T & = c^{2} t^{2} \left( {t(1 - \alpha )(8 + \alpha )\beta^{2} + 3\beta^{2} } \right) + \left( {3\alpha^{2} t^{2} (1 - \alpha )^{2} + 9\alpha \beta t(1 - \alpha )} \right)\left( {c^{2} t + (2c + t)\Delta } \right) \\ & \quad + \;(2c - \Delta )t(2(\alpha t(1 - \alpha ) + 2\beta ) + \beta (t(\alpha (1 - \alpha ) + \beta ) + 8\beta^{2} \Delta t(2c + t) > R > 0. \\ \end{aligned} $$

Therefore, we can derive that $\bar{t}_{RP} > \bar{t}_{RMP} > \bar{t}_{RM} = \bar{t}_{NR} .$ □

1.5 Proof of Proposition 3

We use partial differentiation techniques to investigate the sensitivities of optimal solutions to government subsidy $s$. The proof is similar to the proof of Corollary 1, and thus omitted here. □

1.6 Proof of Proposition 4

According to Eqs. (5), (6), we can derive $CS^{R} = \frac{1}{8t(Q - ct)^{2}}$, and $CS^{RS} = \frac{1}{8t(Q - ct)^{2}}$ under RM, we can derive $CS^{R} = \frac{{t(b^{2} + t^{2} (1 - \alpha )(c^{2} t^{2} + (Q - 2)(Q - 2 + 2ct)\alpha ) + 2ct^{4} (1 - \alpha )\Delta + t^{4} \Delta^{2} + 2bt^{2} (c(1 - \alpha ) + \Delta ))}}{8t(1 - \alpha )\alpha }$, and $CS^{RS} = \frac{{t(b^{2} + t^{2} (1 - \alpha )(c^{2} t^{2} + (Q - 2)(Q - 2 + 2ct)\alpha ) + 2ct^{4} (1 - \alpha )\Delta + t^{4} \Delta^{2} + 2bt^{2} (c(1 - \alpha ) + \Delta ))}}{8t(1 - \alpha )\alpha }$ under RMP, respectively. By comparing the values of $CS^{R}$ and $CS^{RS}$, we can obtain $CS^{R} = CS^{RS}$ under RM and RMP. Thus, the proof of Proposition 4a is completed. Similarly, we can easily prove Proposition 4b, c. □

1.7 Proof of Proposition 5

According to Eq. (7), we can derive $RR^{R} = \frac{b}{(Q - ct)t\beta }$ and $RR^{RS} = \frac{b + s}{(Q - ct)t\beta }$ under RM. By comparing the values of $RR^{R}$ and $RR^{RS}$, we can find $RR^{R} < RR^{RS}$. Similarly, based on Eqs. (10), (11), we can derive $H^{NR} = \frac{{e_{d} (Q - ct)}}{2}$ under NR, and $H^{R} = \frac{{e_{d} ((Q - ct)\beta - b)}}{2\beta }$, $H^{RS} = \frac{{e_{d} ((Q - ct)\beta - b - s)}}{2\beta }$ under RM, respectively. By comparing the values of $H^{NR}$, $H^{R}$ and $H^{RS}$, we can find $H^{R} > H^{RS}$. Similarly, we can have $RR^{R} < RR^{RS}$ and $H^{R} > H^{RS}$ under RMP and RP. Thus, we can obtain Proposition 5a.

Substituting optimal quantities into $RR$ under NR, RM, RMP and RP, respectively, we can obtain $RR_{NR} = 0$, $RR_{RM} = \frac{b}{(Q - ct)t\beta }$, $RR_{RMP} = \frac{bt(1 - \alpha )}{\beta (b + t(Q + Q\alpha - \Delta t))}$, and $RR_{RP} = \frac{{t^{2} (\Delta - c(1 - \alpha ))}}{Q(t\alpha (1 - \alpha ) + \beta ) - t(c\beta + t\alpha \Delta )}$, respectively. Taking the first-order partial derivatives of $RR_{RM}$, $RR_{RMP}$, $RR_{RP}$ with respect to $\Delta$, respectively, we have $\frac{{\partial RR_{RM} }}{\partial \Delta } = 0$,$\frac{{\partial RR_{RMP} }}{\partial \Delta } = \frac{{bt^{3} (1 - \alpha )}}{{\beta (b + t(Q + Q\alpha - \Delta t))^{2} }} > 0$, $\frac{{\partial RR_{RP} }}{\partial \Delta } = \frac{{t^{2} (t\alpha (Q + ct)(1 - \alpha ) + \beta (Q - ct))}}{{(Q(t\alpha (1 - \alpha ) + \beta ) - t(c\beta + t\alpha \Delta ))^{2} }} > 0$. Therefore, $RR_{RM}$ is independent of $\Delta$, but $RR_{RMP}$ and $RR_{RP}$ increase with $\Delta$. Substituting $\bar{\Delta }_{1}$ and $\bar{\Delta }_{2}$ into $RR$ under RM, we can obtain $RR_{{RM/\bar{\Delta }_{1} }} = \frac{b}{(Q - ct)t\beta }$ and $RR_{{RMP/\bar{\Delta }_{2} }} = \frac{b}{(Q - ct)t\beta }$. Similarly, we can obtain $RR_{{RMP/\bar{\Delta }_{2} }} = \frac{b}{(Q - ct)t\beta }$, $RR_{{RMP/\bar{\Delta }_{3} }} = \frac{b}{(Q - ct)t\beta - b\alpha }$ and $RR_{{RP/\bar{\Delta }_{3} }} = \frac{b}{(Q - ct)t\beta - b\alpha }$.

Thus, we have $RR_{RM} = \frac{b}{(Q - ct)\beta }$ when $\bar{\Delta }_{1} \le \Delta < \bar{\Delta }_{2}$; $\frac{b}{(Q - ct)t\beta } \le RR_{RMP} < \frac{b}{(Q - ct)t\beta - b\alpha }$ when $\bar{\Delta }_{2} \le \Delta < \bar{\Delta }_{3}$ and $\frac{b}{(Q - ct)t\beta - b\alpha } \le RR_{RP}$ when $\bar{\Delta }_{3} \le \Delta$. By comparing the values of $RR_{NR}$, $RR_{RMP}$, $RR_{RM}$ and $RR_{RP}$, we have $RR_{NR} < RR_{RM} \le RR_{RMP} < RR_{RP}$. Using the same techniques, we can obtain $H_{NR} > H_{RM} \ge H_{RMP} > H_{RP}$. Thus, we can prove Proposition 5b. □