The impacts of dual overconfidence behavior and demand updating on the decisions of port service supply chain: a real case study from China

Abstract

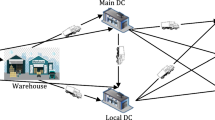
In this paper, the impacts of dual overconfidence behavior and demand updating on the decisions of port service supply chain are studied with the real case study method. A port service supply chain consists of Tianjin Port, a shipping company, and a customer is investigated. A dual overconfidence behavior-based decision model under a demand updating background is built. Then the effects of Tianjin Port’s overconfidence (TPO) behavior and the shipping company’s overconfidence (SCO) behavior on the port service level (PSL), carrying volume and utilities are analyzed. Numerical analysis with real case data is conducted. Several important conclusions are obtained in this paper. Firstly, it is identified that the SCO leads to a decrease in the shipping company’s utilities, while dual overconfidence behavior causes the increase of Tianjin Port’s utilities. Secondly, it is found that the effect of the SCO on the PSL and the effect of TPO on the PSL offset each other which will lead to a threshold in TPO. This threshold is affected by the SCO, and demand updating amplifies this effect. Thirdly, demand updating not only adds to the shipping company’s carrying volume and PSL, but also increases the utilities of both parties. Lastly, it is unexpectedly found that there are interactions between demand updating and dual overconfidence behavior.

Appendices

Appendix A : Proof of Lemma 1

$$ \frac{{\partial Q_{k1}^{*} }}{\partial k} = \left( {b - a} \right)\frac{\gamma w + g}{{f\left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)k^{2} (p + h + g)}} > 0 $$

$$ \frac{{\partial \beta_{l1}^{*} }}{\partial k} = \frac{{\left( {w - v - c} \right)\left( {h\left( {\bar{\beta }} \right) - h\left( {\underline{\beta } } \right)} \right)}}{{le \cdot f\left( {\frac{{k\left( {p + h + g} \right) - \gamma w - g}}{{k\left( {p + h + g} \right)}}} \right)}} \cdot \frac{\gamma w + g}{{k^{2} \left( {p + h + g} \right)}} > 0 $$

$$ \frac{{\partial \beta_{l1}^{*} }}{\partial l} = - \frac{{\left( {w - v - c} \right)\left( {h\left( {\bar{\beta }} \right) - h\left( {\underline{\beta } } \right)} \right)F^{ - 1} \left( {\frac{{k\left( {p + h + g} \right) - \gamma w - g}}{{k\left( {p + h + g} \right)}}} \right)}}{{l^{2} e}} < 0 $$

Similarly, $\frac{{\partial Q_{k2}^{*} }}{\partial k} > 0$, $\frac{{\partial \beta_{l2}^{*} }}{\partial k} > 0$, and $\frac{{\partial \beta_{l2}^{*} }}{\partial l} < 0$ can be proved

Appendix B: Proof of proposition 1

$$ Q_{k1}^{*} - Q_{1}^{*} = \left( {b - a} \right)\left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\} $$

(1)

$$ \begin{aligned} \because \frac{(p + h + g)k - \gamma w - g}{k(p + h + g)} - \frac{p + h - \gamma w}{p + h + g} \hfill \\ \;\;\; = \frac{{\left( {k - 1} \right)(g + \gamma w)}}{k(p + h + g)} \hfill \\ \end{aligned} $$

As $F^{ - } \left( x \right)$ is a monotonically increasing function, therefore: when $k > 1$, $F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) > F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})$, and $Q_{k1}^{*} - Q_{1}^{*} > 0$ when $\frac{\gamma w + g}{p + h + g} < k < 1$, $F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) < F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})$, and $Q_{k1}^{*} - Q_{1}^{*} > 0$

$$ Q_{k2}^{*} - Q_{2}^{ *} = \left( {b - a} \right)\left( F^{ - 1} \left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right) - F^{ - 1} \left( {\frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right) \right) $$

(2)

,We must compare the value of $\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}$ and

$$ \frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}} $$

Further, we have:

$$ \begin{aligned} &\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)} - \frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} - I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}} \hfill \\ &\quad= \frac{\gamma w + g}{k(p + h + g)}\left( {k\left( {1 - I} \right) + \left( {I_{k} - 1} \right)} \right) \hfill \\&\quad \because k\left( {1 - I} \right) > \frac{{k\left( {\gamma w + g} \right)}}{p + h + g},I_{k} - 1 < - \frac{\gamma w + g}{{k\left( {p + h + g} \right)}} \\&\quad \therefore \frac{\gamma w + g}{p + h + g} < k < 1,Q_{k2}^{*} < Q_{2}^{*} ;k > 1,Q_{k2}^{*} > Q_{2}^{*}\end{aligned} $$

Appendix C: Proof of proposition 2

$$ \beta_{l1}^{*} - \beta_{1}^{*} = \frac{{(w - v - c)\left( {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - lF^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right)}}{le} \cdot \left( {h(\bar{\beta }) - h(\underline{\beta } )} \right) $$

We must compare the value of $F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)$ and $lF^{ - 1} (\frac{p + h - \gamma w}{p + h + g})$

As $F^{ - 1} \left( x \right)$ is a monotonically increasing function, therefore:

We only must compare the value of $\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}$ and $\frac{p + h - \gamma w}{p + h + g}$

• (1) When $k > 1$ and $l_{\hbox{min} } < l < 1$

  We have $F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) > lF^{ - 1} (\frac{p + h - \gamma w}{p + h + g})$, so $\beta_{l1}^{*} > \beta_{1}^{*}$

• (2) When $\frac{\gamma w + g}{p + h + g} < k < 1$ and $1 < l < l_{\hbox{max} }$

  We have $F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) < lF^{ - 1} (\frac{p + h - \gamma w}{p + h + g})$, so $\beta_{l1}^{*} < \beta_{1}^{*}$

• (3) When $\frac{\gamma w + g}{p + h + g} < k < 1$ and $l_{\hbox{min} } < l < 1$, we have:

$$ \begin{aligned}& F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - lF^{ - 1} (\frac{p + h - \gamma w}{p + h + g})\\ & \quad > l\left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\} \hfill \\ &\therefore \beta_{l1}^{*} - \beta_{1}^{*} > \frac{{(w - v - c)\left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\}}}{e} \cdot \left( {h(\beta_{0} + \tilde{\beta }) - h(\beta_{0} - \tilde{\beta })} \right) \hfill \\ & \because \frac{\gamma w + g}{p + h + g} < k < 1 \hfill \\ & \therefore \left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\} < 0 \hfill \\ \end{aligned} $$

and we cannot confirm the positive and negative of $\beta_{l1}^{*} - \beta_{1}^{*}$

Let $\beta_{l1}^{*} - \beta_{1}^{*} = 0$, we have

$$ l = \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}} $$

$$ \begin{aligned} \because \frac{\gamma w + g}{p + g + h} < k < 1 \hfill \\ \therefore 0 < l = \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}} < 1 \hfill \\ \end{aligned} $$

In the case of $\frac{\gamma w + g}{p + h + g} < k < 1$

we have $0 < l < \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}} < 1$, and $\beta_{l1}^{*} > \beta_{1}^{*}$

In the case of $\frac{\gamma w + g}{p + h + g} < k < 1$

we have $\frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}} < l < 1$, and $\beta_{l1}^{*} < \beta_{1}^{*}$

(4) When $k > 1$ and $1 < l < l_{\hbox{max} }$

$$ \begin{aligned}& F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - lF^{ - 1} (\frac{p + h - \gamma w}{p + h + g})\\ & \quad < l\left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\} \hfill \\ & \therefore \beta_{l1}^{*} - \beta_{1}^{*} < \frac{{(w - v - c)\tau \left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\}}}{e} \hfill \\ & \because k > 1 \hfill \\ & \therefore \frac{{(w - v - c)\tau \left\{ {F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right\}}}{e} > 0 \hfill \\ \end{aligned} $$

Further, we cannot confirm the positive and negative of $\beta_{l1}^{*} - \beta_{1}^{*}$

Let $\beta_{l1}^{*} - \beta_{1}^{*} = 0$; we have $l = \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}}$

$$ \begin{aligned}& \because k > 1 \hfill \\ & \therefore l = \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}} > 1 \hfill \\ \end{aligned} $$

In the case of $k > 1$

We have $1 < l < \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}}$, and $\beta_{l1}^{*} > \beta_{1}^{*}$

In the case of $k > 1$

We have $1 < \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}} < l$, and $\beta_{l1}^{*} < \beta_{1}^{*}$

In summary

When $l < \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}},\beta_{l1}^{*} > \beta_{1}^{*}$;

While $l > \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}},\beta_{l1}^{*} < \beta_{1}^{*}$

Since $\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}{ = 1} - \frac{{\left( {\gamma w + g} \right)}}{k(p + h + g)}$ increases monotonically with $k$, $F^{ - 1} \left( x \right)$ is an increase function as well.

We can prove that $F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)$ increases monotonically with $k$.

Therefore $A_{1} = \frac{{F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}}{{F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})}}$ increases monotonically with $k$.

Similarly, we can prove the relationship between $\beta_{l2}^{*}$ and $\beta_{2}^{*}$, and $A_{2}$ increases monotonically with $k$, as described in Proposition 2.

Appendix D: Proof of Lemma 2

We need to compare $A_{1}$ and 1; $A_{1} = \frac{{F^{ - 1} \left( {\frac{{k\left( {p + h + g} \right) - \left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}}} \right)}}{{F^{ - 1} \left( {\frac{p + h - \gamma w}{{\left( {p + h + g} \right)}}} \right)}}$

We first compare the value of $\frac{{k\left( {p + h + g} \right) - \left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}}$ and $\frac{p + h - \gamma w}{{\left( {p + h + g} \right)}}$.

We have:

$$ \begin{aligned} \frac{{k\left( {p + h + g} \right) - \left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}} - \frac{p + h - \gamma w}{{\left( {p + h + g} \right)}} \hfill \\ = \frac{{\left( {k - 1} \right)\left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}} \hfill \\ \end{aligned} $$

Therefore, when $\frac{g + \gamma w}{p + h + g} < k < 1$, $A < 1$; and when $\frac{g + \gamma w}{p + h + g} \ge 1$, $A \ge 1$.

$$ \frac{\partial A}{\partial k} = \frac{g + \gamma w}{{F^{ - 1} \left( {\frac{p + h - \gamma w}{{\left( {p + h + g} \right)}}} \right) \cdot f\left( {\frac{{k\left( {p + h + g} \right) - \left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}}} \right) \cdot k^{2} \left( {p + h + g} \right)}} > 0 $$

Appendix E: Proof of proposition 3

In the context of no demand updating, compared with the rational situation, in the case of dual overconfidence conditions, the utility change of the shipping company is as follows:

$$ \Delta \varPi_{S1} = \varPi_{S1}^{k} - \varPi_{S1} = \left( {p + h - \gamma w} \right)\left( {Q_{k1}^{*} - Q_{1}^{*} } \right) - \left( {p + h + g} \right)\left( {\hat{\beta }_{1} \int_{0}^{{\frac{{Q_{k1}^{*} }}{{\hat{\beta }_{1} }}}} {F\left( x \right)dx - \hat{\beta }_{1} \int_{0}^{{\frac{{Q_{1}^{*} }}{{\hat{\beta }_{1} }}}} {F\left( x \right)dx} } } \right) $$

After updating the demand, compared with the rational situation, in the case of dual overconfidence conditions, the utility change of the shipping company is as follows:

$$ \Delta \varPi_{S2} = \varPi_{S2}^{k} - \varPi_{S2} = \left( {p + h - \gamma w} \right)\left( {Q_{k2}^{*} - Q_{2}^{*} } \right) - \left( {p + h + g} \right)\left( {\hat{\beta }_{2} \int_{0}^{{\frac{{Q_{k2}^{*} }}{{\hat{\beta }_{2} }}}} {G\left( x \right)dx - \hat{\beta }_{2} \int_{0}^{{\frac{{Q_{2}^{*} }}{{\hat{\beta }_{2} }}}} {G\left( x \right)dx} } } \right) $$

Take the first derivative of $\Delta \varPi_{\text{S1}}$ with respect to $k$, and we have:

$$ \begin{aligned} \frac{{\partial \Delta \varPi_{S1} }}{\partial k} = \left( {p + h - \gamma w} \right)\frac{{\partial Q_{k1}^{*} }}{\partial k} - \left( {p + h + g} \right)F\left( {\frac{{Q_{k1}^{*} }}{{\hat{\beta }_{1} }}} \right)\frac{{\partial Q_{k1}^{*} }}{\partial k} \hfill \\ \;\;\;\;\;\;\;\;\;\;\; = \left( {\gamma w + g} \right)\left( {\frac{ 1}{k} - 1} \right)\frac{{\partial Q_{k1}^{*} }}{\partial k} \hfill \\ \;\;\;\;\;\;\;\;\;\;\; = \left( {\gamma w + g} \right)\left( {\frac{ 1}{k} - 1} \right)\left( {b - a} \right)\frac{{\left( {\frac{\gamma w + g}{{k^{2} (p + h + g)}}} \right)}}{{F\left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)}} \hfill \\ \end{aligned} $$

When $k = 1$, $\frac{{\partial \Delta \varPi_{S1} }}{\partial k} = 0$; when $\frac{g + \gamma w}{p + g + h} < k < 1$, $\frac{{\partial \Delta \varPi_{S1} }}{\partial k} > 0$; when $k > 1$, $\frac{{\partial \Delta \varPi_{S1} }}{\partial k} < 0$.

In addition, since $k = 1$, we obtain $\Delta \varPi_{S1} = 0$, that is, $\varPi_{S1}^{k} = \varPi_{S1}$.

Therefore $\Delta \varPi_{S1} \le 0$.

The proof of $\Delta \varPi_{S2}$ is similar to $\Delta \varPi_{S1}.$

Appendix F: A Proof of proposition 4

$$ \begin{aligned}& Q_{2}^{*} - Q_{1}^{*} = \left( {b - a} \right)\left( {F^{ - 1} \left( {\frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right) \hfill \\ &\quad\because \frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}} - \frac{p + h - \gamma w}{p + h + g} = I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}} > 0 \hfill \\ &\quad\therefore F^{ - 1} \left( {\frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right) > F^{ - 1} \left(\frac{p + h - \gamma w}{p + h + g}\right) \hfill \\ &\therefore Q_{2}^{*} > Q_{1}^{*} \hfill \\ \end{aligned} $$

$$\begin{aligned} &\beta_{2}^{*} - \beta_{1}^{*} = \frac{{(w - v - c)\left( {h(\bar{\beta }) - h(\underline{\beta } )} \right)}}{e}\nonumber\\ &\quad \left[ {F^{ - 1} \left( {\frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right) - F^{ - 1} (\frac{p + h - \gamma w}{p + h + g})} \right] \end{aligned}$$

$$ \begin{aligned} & \because \frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}} - \frac{p + h - \gamma w}{p + h + g} = I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}} > 0 \hfill \\ & \therefore F^{ - 1} \left( {\frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right) > F^{ - 1} \left(\frac{p + h - \gamma w}{p + h + g}\right) \hfill \\ &\therefore \beta_{2}^{*} > \beta_{1}^{*} \hfill \\ \end{aligned} $$

$$ \begin{aligned} & \beta_{l2}^{*} - \beta_{l1}^{*}= \frac{{(w - v - c)\left( {h(\bar{\beta }) - h(\underline{\beta } )} \right)}}{le}\nonumber\\ &\quad \left[ {F^{ - 1} \left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right) - F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)} \right]\; \end{aligned}$$

$$ \begin{aligned} &\because \frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)} - \frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} = \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)} > 0 \hfill \\ &\therefore F^{ - 1} \left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right) > F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) \hfill \\ &\therefore \beta_{l2}^{*} > \beta_{l1}^{*} \hfill \\ \end{aligned} $$

$$ \begin{aligned}& Q_{k2}^{*} - Q_{k1}^{*} = \left( {b - a} \right)\nonumber\\ &\quad \left[ {F^{ - 1} \left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right) - F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right)} \right] \end{aligned}$$

$$ \begin{aligned} &\because \frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)} - \frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} = \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)} > 0 \hfill \\ &\therefore F^{ - 1} \left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right) > F^{ - 1} \left( {\frac{(p + h + g)k - \gamma w - g}{k(p + h + g)}} \right) \hfill \\ &\therefore Q_{k2}^{*} > Q_{k1}^{*} \hfill \\ \end{aligned} $$

Appendix G: Proof the proposition 5

$$ \begin{aligned} A_{2} - A_{1} = \frac{{F^{ - 1} \left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right)}}{{F^{ - 1} \left( {\frac{{k\left( {p + h + g} \right) - \left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}}} \right)}} - \frac{{F^{ - 1} \left( {\frac{{\left( {p + h - \gamma w} \right)}}{{\left( {p + h + g} \right)}} + I \cdot \frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right)}}{{F^{ - 1} \left( {\frac{p + h - \gamma w}{{\left( {p + h + g} \right)}}} \right)}} \hfill \\ \frac{{\partial \left( {A_{2} - A_{1} } \right)}}{\partial k} = \frac{{f\left( {\frac{{k\left( {p + h + g} \right) - \left( {g + \gamma w} \right)}}{{k\left( {p + h + g} \right)}}} \right)}}{{f\left( {\frac{{k(p + h + g) - \left( {\gamma w + g} \right)}}{k(p + h + g)} + \frac{{I_{k} \left( {\gamma w + g} \right)}}{k(p + h + g)}} \right)}} \cdot \frac{{2\left( {\frac{{\left( {g + \gamma w} \right)}}{{\left( {p + h + g} \right)}}} \right)}}{k} > 0 \hfill \\ \end{aligned} $$

Therefore, $A_{2} - A_{1}$ increases with k.

Further, when $k = 1$, $A_{2} - A_{1} = 0$, $A_{2} = A_{1}$.

Hence, when $k < 1$, $A_{2} - A_{1} < 0$, $A_{2} < A_{1}$.

Otherwise, when $k > 1$, $A_{2} - A_{1} > 0$, $A_{2} > A_{1}$.