The Dynkin game with regime switching and applications to pricing game options

Abstract

This paper is concerned with the Dynkin game (a zero-sum optimal stopping game). The dynamic of the system is modeled by a regime switching diffusion, in which the regime switching mechanism provides the structural changes of the random environment. The goal is to find a saddle point for the payoff functional up to one of the players exiting the game. Taking advantage of the method of penalization and the dynamic programming principle, the value function of the game problem is shown to be the unique viscosity solution to the associated variational inequalities. We also consider a financial example of pricing game option under a regime switching market. Both optimal stopping rules for the buyer and the seller and fair price of the option are numerically demonstrated in this example. All the results are markedly different from the traditional cases without regime switching.

1 Introduction

The Dynkin game is a problem that multiple players make decisions by using stopping times, according to their own advantages and trade-off with other peers, in the context of dynamic systems. The theory of the Dynkin game has been extensively studied along the line of classical variational inequalities method; see Bensoussan and Friedman (1974); Bensoussan (1982); Kamizono and Morimoto (2002); Akdim et al. (2006), among others. The other important approach is the utilization of doubly reflected backward stochastic differential equations (BSDEs for short). The pioneering work on this subject is Cvitanic and Karatzas (1996). Then the results were extended by Hamadène and Lepeltier (2000), Hamadène (2006), Bayraktar and Yao (2015), Grigorova et al. (2018), and so on. In contrast to the variational inequalities method, the doubly reflected BSDEs approach is able to deal with the finite horizon Dynkin game problems in non-Markovian context. For the infinite horizon case, there are few results, see for example, Hamadène et al. (1999), which are however not effective to treat the Dynkin game problems.

Note that all of the aforementioned literature on the Dynkin games are concerned with Itô diffusions. Due to the capacity for characterizing various random events and the tractability, which enables advanced mathematical analysis and feasible numerical schemes to be developed, regime switching models have drawn considerable attention from both academia researchers and practitioners in recent years. Some of such examples can be found in mathematical finance (Zhang 2001; Zhou and Yin 2003), stochastic manufacturing systems (Sethi and Zhang 1994; Zhang 1995), and risk management (Elliott and Siu 2010; Zhu 2011). To be precise, compared with the conventional diffusion models, regime switching models have two distinct advantages. First, the underlying Markov chain can be used to model discrete events that have greater long-term system impact. For example, in connection with financial markets, market trends can be easily captured in terms of a finite-state Markov chain. Such dynamic is nevertheless difficult to be incorporated into a pure diffusion model. Second, regime switching models require very limited data input when performing numerical simulations, e.g., in Zhang (2001), only the stock appreciation rate and volatility rate for each state of the Markov chain and the corresponding Q matrix are needed to compute the optimal trading rule. For further details and more illustrations about regime switching models, the reader is referred to the books by Yin and Zhang (2013) and Yin and Zhu (2010).

In this paper, we consider the Dynkin game problem with regime switching in an infinite horizon. The problem is formulated as follows. Let $({\varOmega },{\mathcal {F}},P)$ be a fixed probability space on which are defined a standard one-dimensional Brownian motion B(t), $t\ge 0$ and a Markov chain $\alpha (t)$, $t\ge 0$. Assume that $B(\cdot )$ and $\alpha (\cdot )$ are independent. The Markov chain is observable and takes values in a finite state space ${\mathcal {M}}=\{1,\dots ,M\}$. Denote $Q=(\lambda _{pq})_{p,q\in {\mathcal {M}}}$ the generator of $\alpha (\cdot )$ with $\lambda _{pq}\ge 0$ for $p\ne q$ and $\sum _{q\in {\mathcal {M}}}\lambda _{pq}=0$ for each $p\in {\mathcal {M}}$. Let $\{{\mathcal {F}}_{t}\}_{t\ge 0}$ be the natural filtration generated by $B(\cdot )$ and $\alpha (\cdot )$ and augmented by the null sets.

Consider a one-dimensional switching diffusion $(\alpha ^{p}(\cdot ),X^{p,x}(\cdot ))$ with initial state $(p,x)\in {\mathcal {M}}\times R$:

$$\begin{aligned} \left\{ \begin{aligned} dX^{p,x}(t)=&b(\alpha ^{p}(t),X^{p,x}(t))dt+ \sigma (\alpha ^{p}(t),X^{p,x}(t))dB(t),\quad t\ge 0,\\ X^{p,x}(0)=&x,\quad \alpha ^{p}(0)=p, \end{aligned} \right. \end{aligned}$$

(1)

where b and $\sigma$ are two suitable functions. Assume we have two players, $A_{1}$ and $A_{2}$. The system (1) works or is alive up to the time when one of the players decides to exit at a stopping time $\tau _{1}$ for $A_{1}$ or $\tau _{2}$ for $A_{2}$. The actions of the players are not free and their advantages are antagonistic, i.e., between $A_{1}$ and $A_{2}$ there is a payoff $J(\tau _{1},\tau _{2})$ given below which is a cost for $A_{1}$ and a reward for $A_{2}$:

$$\begin{aligned} \begin{aligned} J(\tau _{1},\tau _{2})&=E\bigg [\int _{0}^{\tau _{1}\wedge \tau _{2}}e^{-\rho t}f(\alpha ^{p}(t),X^{p,x}(t))dt\\&\quad +e^{-\rho (\tau _{1}\wedge \tau _{2})} \bigg (g(\alpha ^{p}(\tau _{1}),X^{p,x}(\tau _{1}))1_{\{\tau _{1}<\tau _{2}\}} +h(\alpha ^{p}(\tau _{2}),X^{p,x}(\tau _{2}))1_{\{\tau _{1} \ge \tau _{2}\}}\bigg )\bigg ], \end{aligned}\nonumber \\ \end{aligned}$$

(2)

where $\rho >0$ is a given discount factor, f, g, and h are given functions. Note that the Markov chain involved in (1) and (2) serves as a driving force to depict the environmental changes.

The problem under consideration is about finding a pair of stopping times $(\tau _{1}^{*},\tau _{2}^{*})$ with the payoff functional $J(\tau _{1},\tau _{2})$ satisfying

$$\begin{aligned} J(\tau _{1}^{*},\tau _{2})\le J(\tau _{1}^{*},\tau _{2}^{*})\le J(\tau _{1},\tau _{2}^{*}), \text{ for } \text{ any } (\tau _{1},\tau _{2}). \end{aligned}$$

The property of $(\tau _{1}^{*},\tau _{2}^{*})$ means that when the players $A_{1}$ and $A_{2}$ stop with $\tau _{1}^{*}$ and $\tau _{2}^{*}$, respectively, it is advantageous for both to keep the same stopping times. Otherwise, if one of them decides unilaterally to change a strategy, it is penalized if the other keeps its initial one. Actually, when $A_{1}$ chooses $\tau _{1}^{*}$ as the stopping time, then the best choice for $A_{2}$ is to stop at $\tau _{2}^{*}$. If $A_{2}$ deviates, it would get a less amount than what it would obtain if stops at $\tau _{2}^{*}$. Conversely if $A_{2}$ chooses to stop at $\tau _{2}^{*}$, then the best choice for $A_{1}$ is to stop at $\tau _{1}^{*}$; otherwise $A_{1}$ will pay a greater amount. We call such pair $(\tau _{1}^{*},\tau _{2}^{*})$ a saddle point for the game. Additionally, this existence implies in particular that

$$\begin{aligned} v(p,x)\doteq \inf _{\tau _{1}}\sup _{\tau _{2}}J(\tau _{1},\tau _{2}) =\sup _{\tau _{2}}\inf _{\tau _{1}}J(\tau _{1},\tau _{2}), \end{aligned}$$

i.e., the game has a value; for notational simplicity, we also denote $v_{p}(x)$ for v(p, x) interchangeably.

We shall follow the variational inequalities method to solve the game problem. Formally, the associated variational inequalities in the present case is a system of second order ordinary differential equations (ODEs) with double obstacles taking the following form:

$$\begin{aligned} \begin{aligned}&\min \bigg \{\max \bigg \{\rho v_{p}(x)-{\mathcal {L}}_{p}v_{p}(x)-f(p,x) -Qv(\cdot ,x)(p),v_{p}(x)-g(p,x)\bigg \},\\&\qquad v_{p}(x)-h(p,x)\bigg \}=0, \end{aligned} \end{aligned}$$

(3)

where ${\mathcal {L}}_{p}=b(p,x)\frac{\partial }{\partial x} +\frac{1}{2}\sigma ^{2}(p,x)\frac{\partial ^{2}}{\partial x^{2}}$ and $Qv(\cdot ,x)(p)=\sum _{q\ne p}\lambda _{pq}(v(q,x)-v(p,x))$. By means of the method of penalization (Morimoto 2003) and the dynamic programming principle (Fleming and Soner 2006; Yong and Zhou 1999), we will show that the value of the Dynkin game is exactly the unique viscosity solution of (3). In addition, the saddle point will be given explicitly.

An important application of the Dynkin game is the pricing of game options introduced in Kifer (2000); see also Ekström (2006), Dolinsky (2013), Dumitrescu et al. (2017), among others. A game option is a contract which allows both the buyer and the seller to terminate the contract at any time. In particular, the buyer can terminate the contract by exercising the right to buy (call option) or to sell (put option) the underlying security for certain agreed price. On the other hand, if the seller cancels the contract, a penalty is imposed and must be paid to the buyer. It turns out immediately that the pricing of game options falls into the framework of the Dynkin game. In this paper, we will apply the general theory of the Dynkin game to pricing game options in a regime switching market. Not only the fair price, but also the optimal stopping time for the buyer (respectively, seller) to exercise (respectively, cancel) the option will be numerically computed.

The main contributions of this paper include two aspects, as follows:

On the one hand, we develop the variational inequalities method for the Dynkin game problem under a regime switching model. Compared with the similar problem but under a pure diffusion model, which was initially treated by Morimoto (2003), we alternatively use a more intuitive approach, i.e., approximation scheme of stopping time, to show the dynamic programming principle is valid for the penalized problem. Moreover, the HJB equation or variational inequalities is now a coupled system of second order differential equations [see (6) and (3)] in lieu of a single differential equation when there is no regime switching. This feature adds much difficulty in the analysis, in particular, these equations are not proper in the sense of Crandall et al. (1992). Note that the properness was an essential assumption to derive the strong comparison result and hence the uniqueness of the viscosity solution in Crandall et al. (1992). Here we need to carefully handle the coupling term $Qv^{\varepsilon }(\cdot ,x)(p)$; see the proof of Theorem 2 for details.

On the other hand, it is worthy of being mentioned that, this paper is the first effort to study the pricing problem of game options in a regime switching market. Despite the widely accepted belief that market trends will significantly affect the decisions made by the agents, a quantitative measure is in general desirable. The numerical experiment conducted in this paper exhibits clearly the influence of regime switching of the market on the behaviors of the agents (buyer and seller). From this point of view, this paper should be distinguished from Kifer (2000), Hamadène (2006), Hamadène and Zhang (2010), etc., where the Markov chains are not involved, and Guo and Zhang (2004) and Guo and Zhang (2005), which studied the American option pricing problems (or, optimal selling rules for a stock) with regime switching, i.e., in their settings there is only one player that can make decision.

The plan of this paper is as follows. In the next section, we consider the penalized problem for the original Dynkin game problem. With the help of the dynamic programming principle, we show that the value function of penalized problem is the unique viscosity solution of the associated penalized HJB equation. In Sect. 3, it is proved that the unique viscosity solution of penalized HJB equation converges to that of variational inequalities (3). Then, in Sect. 4, we provide a numerical example concerned with the pricing of game options. Finally, we conclude the paper by making further remarks.

2 Penalized problem

Let ${\mathcal {A}}$ denote the Banach space of all bounded and uniformly continuous (with respect to the spatial variable x) functions $\varphi (p,x):{\mathcal {M}}\times R\mapsto R$ with norm $\Vert \varphi \Vert =\max _{p\in {\mathcal {M}}}\sup _{x\in R}|\varphi (p,x)|$. In this section, we consider a penalized problem parameterized by $\varepsilon >0$ for the original Dynkin game problem:

$$\begin{aligned} \begin{aligned} v^{\varepsilon }(p,x) =E\int _{0}^{\infty }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg ) (\alpha ^{p}(t),X^{p,x}(t))dt, \quad \varepsilon >0, \end{aligned}\nonumber \\ \end{aligned}$$

(4)

where $X^{p,x}(t)$ is given by (1). In fact, it is an equation with $v^{\varepsilon }$ as the unknown.

Throughout the paper, we make the following assumptions:

• (A1) There exists a positive constant L such that

  $$\begin{aligned} \begin{aligned}&|b(p,x)|+|\sigma (p,x)|\le L(1+|x|),\\&|b(p,x)-b(p,y)|+|\sigma (p,x)-\sigma (p,y)|\le L|x-y|, \end{aligned} \end{aligned}$$

  for any $p\in {\mathcal {M}}$ and $x,y\in R$.

• (A2) f, g, and $h\in {\mathcal {A}}$. In addition, for any $p\in {\mathcal {M}}$ and $x\in R$, we have $h(p,x)\le g(p,x)$.

• (A3) $\rho > L^{2}+2L$.

Based on the fixed point theorem, we can establish the wellposedness of (4).

Lemma 1

Assume (A1)–(A3). Then, Eq. (4) admits a unique solution $v^{\varepsilon }\in {\mathcal {A}}$.

At this step, it turns out that (1) and (4) can be regarded as a “control problem” involving no control variable (or trivial control variable). The following lemma presents the corresponding dynamic programming principle for this “control problem.”

Lemma 2

Assume (A1)–(A3). Then, for any $(p,x)\in {\mathcal {M}}\times R$ and any stopping time $\theta$, we have

$$\begin{aligned} \begin{aligned} v^{\varepsilon }(p,x)&=E\bigg [\int _{0}^{\theta } e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(\alpha ^{p}(t),X^{p,x}(t))dt \\&\quad +e^{-(\rho +\frac{2}{\varepsilon })\theta } v^{\varepsilon }(\alpha ^{p}(\theta ),X^{p,x}(\theta ))\bigg ]. \end{aligned} \end{aligned}$$

(5)

Proof

We divide the proof into two steps.

Step 1. At first, consider the case when $\theta$ takes at most countably many values $\{t_{1},t_{2},\ldots \}$ with $t_{m+1}>t_{m}$ and $t_{m}\rightarrow \infty$ as $m\rightarrow \infty$.

Note that

$$\begin{aligned} \begin{aligned}&E\int _{\theta }^{\infty } e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(\alpha ^{p}(t),X^{p,x}(t))dt\\&\quad =\sum _{m=1}^{\infty }E\bigg [1_{\{\theta =t_{m}\}} \int _{t_{m}}^{\infty }e^{-(\rho +\frac{2}{\varepsilon })t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg ) (\alpha ^{p}(t),X^{p,x}(t))dt\bigg ]. \end{aligned} \end{aligned}$$

Changing of variable $t \mapsto t+t_{m}$ leads to

$$\begin{aligned} \begin{aligned}&E\bigg [1_{\{\theta =t_{m}\}}\int _{t_{m}}^{\infty } e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(\alpha ^{p}(t),X^{p,x}(t))dt\bigg ]\\&\quad =E\bigg [1_{\{\theta =t_{m}\}}e^{-(\rho +\frac{2}{\varepsilon }) t_{m}} \int _{0}^{\infty }e^{-(\rho +\frac{2}{\varepsilon }) t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g\\&\qquad +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(\alpha ^{p}(t+t_{m}),X^{p,x}(t+t_{m}))dt\bigg ]. \end{aligned} \end{aligned}$$

Moreover, taking conditional expectation and using the Markov property yield

$$\begin{aligned} \begin{aligned}&E\bigg [\int _{0}^{\infty }e^{-(\rho +\frac{2}{\varepsilon }) t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg ) (\alpha ^{p}(t+t_{m}),X^{p,x}(t+t_{m}))dt \bigg |{\mathcal {F}}_{t_{m}}\bigg ]\\&\quad =E\bigg [\int _{0}^{\infty }e^{-(\rho +\frac{2}{\varepsilon }) t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g\\&\qquad +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(\alpha ^{p}(t+t_{m}),X^{p,x}(t+t_{m}))dt \bigg |\alpha ^{p}(t_{m}),X^{p,x}(t_{m})\bigg ]\\&\quad = v^{\varepsilon }(\alpha ^{p}(t_{m}),X^{p,x}(t_{m})). \end{aligned} \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned}&E\int _{\theta }^{\infty }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(\alpha ^{p}(t),X^{p,x}(t))dt\\&\quad =\sum _{m=1}^{\infty }E\bigg [1_{\{\theta =t_{m}\}} e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t_{m}} v^{\varepsilon }(\alpha ^{p}(t_{m}),X^{p,x}(t_{m}))\bigg ]\\&\quad =Ee^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )\theta } v^{\varepsilon }(\alpha ^{p}(\theta ),X^{p,x}(\theta )). \end{aligned} \end{aligned}$$

Hence, (5) holds.

Step 2. In this step, we consider a general stopping time $\theta$. For any $r=1,2,\ldots$, let

$$\begin{aligned} \begin{aligned} \theta _{r}=\sum _{l=1}^{\infty }\frac{l}{2^{r}} 1_{\left\{ \frac{l-1}{2^{r}}<\theta \le \frac{l}{2^{r}}\right\} }. \end{aligned} \end{aligned}$$

Then $\theta _{r}$ is also an ${\mathcal {F}}_{t}$-stopping time because $\{\theta _{r}\le t\}=\{\theta \le \frac{l_{0}}{2^{r}}\} \in {\mathcal {F}}_{\frac{l_{0}}{2^{r}}}\subset {\mathcal {F}}_{t}$, where $l_{0}=\sup \{l:\frac{l}{2^{r}}\le t\}$. Moreover, for each r, $\theta \le \theta _{r}<\theta +\frac{1}{2^{r}}$.

Denote

$$\begin{aligned} \begin{aligned} G(\theta )=&\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg ) (\alpha ^{p}(t),X^{p,x}(t))dt\\&+e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )\theta } v^{\varepsilon }(\alpha ^{p}(\theta ),X^{p,x}(\theta )). \end{aligned} \end{aligned}$$

It suffices to show that

$$\begin{aligned} |EG(\theta )-EG(\theta _{r})|\le E|G(\theta )-G(\theta _{r})| \end{aligned}$$

goes to 0 as $r\rightarrow \infty$.

In view of the right-continuity of $\alpha ^{p}(\cdot )$ and $X^{p,x}(\cdot )$, the uniform continuity of $v^{\varepsilon }$ with respect to x, and the dominated convergence theorem, we have

$$\begin{aligned} \begin{aligned}&E|G(\theta )-G(\theta _{r})|\\&\quad \le E\bigg [\int _{\theta }^{\theta _{r}}e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg |f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg |(\alpha ^{p}(t),X^{p,x}(t))dt\\&\qquad +\bigg |e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta } v^{\varepsilon }(\alpha ^{p}(\theta ),X^{p,x}(\theta )) -e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta _{r}} v^{\varepsilon }(\alpha ^{p}(\theta _{r}),X^{p,x}(\theta _{r}))\bigg |\bigg ] \end{aligned} \end{aligned}$$

converges to 0 as $r\rightarrow \infty$.

This completes the proof. $\square$

Taking advantage of the dynamic programming principle, we will show that $v^{\varepsilon }$ defined by (4) is the unique viscosity solution of the following penalized HJB equation:

$$\begin{aligned} \begin{aligned} \left( \rho {+}\frac{2}{\varepsilon }\right) v^{\varepsilon }_{p}(x) {-}{\mathcal {L}}_{p}v^{\varepsilon }_{p}(x) {-} \left( f{+}\frac{1}{\varepsilon }v^{\varepsilon }\wedge g {+}\frac{1}{\varepsilon }v^{\varepsilon }\vee h\right) (p,x) {-}Qv^{\varepsilon }(\cdot ,x)(p){=}0, \end{aligned} \end{aligned}$$

(6)

or equivalently,

$$\begin{aligned} \begin{aligned} \rho v^{\varepsilon }_{p}(x) {-}{\mathcal {L}}_{p}v^{\varepsilon }_{p}(x) {-}\left( f{-}\frac{1}{\varepsilon }(v^{\varepsilon }{-}g)^{+} {+}\frac{1}{\varepsilon }(v^{\varepsilon }{-}h)^{-}\right) (p,x) {-}Qv^{\varepsilon }(\cdot ,x)(p){=}0. \end{aligned} \end{aligned}$$

(7)

Definition 1

A function $v^{\varepsilon }\in {\mathcal {A}}$ is said to be a viscosity subsolution (resp., supersolution) of (6) if for any $p\in {\mathcal {M}}$,

$$\begin{aligned} \begin{aligned}&\left( \rho +\frac{2}{\varepsilon }\right) v^{\varepsilon }_{p}({\bar{x}}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}) -\left( f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\right) (p,{\bar{x}}) \\&\quad -Qv^{\varepsilon }(\cdot ,{\bar{x}})(p) \le 0, \quad (\text {resp., }\ge 0), \end{aligned} \end{aligned}$$

whenever $\varphi \in C^{2}$ (i.e., twice continuously differentiable) and $v^{\varepsilon }_{p}-\varphi$ has a (strict) local maximum (resp., minimum) at $x={\bar{x}}$. $v^{\varepsilon }$ is called a viscosity solution if it is both a viscosity subsolution and a viscosity supersolution.

Here we give an equivalent definition of viscosity solution of (6), which is useful for proving the uniqueness result. Denote $J^{2,+}v(x)$ the second order superdifferential of v at x:

$$\begin{aligned} \begin{aligned} J^{2,+}v(x)=\bigg \{(\eta ,{\varLambda })\in R\times R: \limsup _{y\rightarrow x}\frac{v(y)-v(x)-(y-x)\eta -\frac{1}{2}(y-x)^{2}{\varLambda }}{|y-x|^{2}}\le 0\bigg \}, \end{aligned} \end{aligned}$$

and the second order subdifferential of v at x is defined by

$$\begin{aligned} J^{2,-}v(x)=-J^{2,+}(-v)(x). \end{aligned}$$

We also denote the closures of $J^{2,+}v(x)$ and $J^{2,-}v(x)$ by ${\bar{J}}^{2,+}v(x)$ and ${\bar{J}}^{2,-}v(x)$, respectively.

Definition 2

A function $v^{\varepsilon }\in {\mathcal {A}}$ is said to be a viscosity subsolution (resp., supersolution) of (6) if for any $(p,x)\in {\mathcal {M}}\times R$ and for any $(\eta ,{\varLambda })\in J^{2,+}v^{\varepsilon }_{p}(x)$ (resp., $J^{2,-}v^{\varepsilon }_{p}(x)$),

$$\begin{aligned} \begin{aligned}&\left( \rho +\frac{2}{\varepsilon }\right) v^{\varepsilon }_{p}(x) -b(p,x)\eta -\frac{1}{2}\sigma ^{2}(p,x){\varLambda }-\left( f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\right) (p,x)\\&\quad -Qv^{\varepsilon }(\cdot ,x)(p) \le 0, \quad (\text {resp., }\ge 0). \end{aligned} \end{aligned}$$

(8)

$v^{\varepsilon }$ is called a viscosity solution if it is both a viscosity subsolution and a viscosity supersolution.

Remark 1

For any $(p,x)\in {\mathcal {M}}\times R$, (8) remains true, for reasons of continuity, if $(\eta ,{\varLambda })\in {\bar{J}}^{2,+}v^{\varepsilon }_{p}(x)$ (resp., ${\bar{J}}^{2,-}v^{\varepsilon }_{p}(x)$); see Crandall et al. (1992, Remark 2.4).

Theorem 1

Assume (A1)–(A3). Then, $v^{\varepsilon }$ defined by (4) is a viscosity solution of (6).

Proof

In view of Definition 1, it suffices to show that $v^{\varepsilon }$ is both a viscosity supersolution and a viscosity subsolution.

Viscosity supersolution property. For any fixed $p\in {\mathcal {M}}$, let $\varphi (x)\in C^{2}$ be such that $v^{\varepsilon }_{p}(x)-\varphi (x)$ attains its minimum at $x={\bar{x}}$ in a neighborhood $B_{\delta }({\bar{x}})=({\bar{x}}-\delta ,{\bar{x}}+\delta )$, for some $\delta >0$. Let $\tau _{\alpha }$ denote the first jump time of $\alpha ^{p}(\cdot )$ and $\tau _{\delta }=\inf \{t\ge 0: X^{p,{\bar{x}}}(t)\notin B_{\delta }({\bar{x}})\}$. Choose $\theta =\tau _{\alpha }\wedge \tau _{\delta }\wedge h$ with $h>0$. Define $\psi :{\mathcal {M}}\times R\rightarrow R$ as follows

$$\begin{aligned} \begin{aligned} \psi (q,x)=\left\{ \begin{array}{l@{\quad }l} \varphi (x)+v^{\varepsilon }_{p}({\bar{x}}) -\varphi ({\bar{x}}),&{} \quad q=p,\\ v^{\varepsilon }_{q}(x), &{} \quad q\ne p. \end{array}\right. \end{aligned} \end{aligned}$$

(9)

Applying Itô’s formula between 0 and $\theta$, we have

$$\begin{aligned} \begin{aligned}&E\bigg [e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta } \psi (\alpha ^{p}(\theta ),X^{p,{\bar{x}}}(\theta ))\bigg ] -\psi (p,{\bar{x}})\\&\quad =E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (-\bigg (\rho +\frac{2}{\varepsilon }\bigg )\psi (p,X^{p,{\bar{x}}}(t)) +{\mathcal {L}}_{p}\varphi (X^{p,{\bar{x}}}(t))\\&\qquad +Q\psi (\cdot ,X^{p,{\bar{x}}}(t))(p)\bigg )dt\bigg ]. \end{aligned} \end{aligned}$$

Moreover, $X^{p,{\bar{x}}}(t)\in B_{\delta }({\bar{x}})$ for $0\le t\le \theta$. Thus, by the definition of $\varphi$,

$$\begin{aligned} \begin{aligned} \varphi (X^{p,{\bar{x}}}(t))\le v^{\varepsilon }_{p}(X^{p,{\bar{x}}}(t)) -(v^{\varepsilon }_{p}({\bar{x}}) -\varphi ({\bar{x}})),\quad 0\le t\le \theta . \end{aligned} \end{aligned}$$

From the above two equations, we deduce that

$$\begin{aligned} \begin{aligned}&E\bigg [e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta } v^{\varepsilon }(\alpha ^{p}(\theta ),X^{p,{\bar{x}}}(\theta ))\bigg ] -v^{\varepsilon }(p,{\bar{x}})\\&\quad \ge E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) v^{\varepsilon }(p,X^{p,{\bar{x}}}(t)) +{\mathcal {L}}_{p}\varphi (X^{p,{\bar{x}}}(t))\\&\qquad +Qv^{\varepsilon }(\cdot ,X^{p,{\bar{x}}}(t))(p)\bigg )dt\bigg ]. \end{aligned} \end{aligned}$$

Furthermore, in view of (5), we have

$$\begin{aligned} \begin{aligned}&E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (\bigg (\rho +\frac{2}{\varepsilon }\bigg )v^{\varepsilon }(p,X^{p,{\bar{x}}}(t)) -{\mathcal {L}}_{p}\varphi (X^{p,{\bar{x}}}(t))\\&\qquad -\bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )(p,X^{p,{\bar{x}}}(t)) -Qv^{\varepsilon }(\cdot ,X^{p,{\bar{x}}}(t))(p)\bigg )dt\bigg ]\ge 0. \end{aligned} \end{aligned}$$

Dividing both sides of the above inequality by h and letting $h\rightarrow 0$, it follows that

$$\begin{aligned} \begin{aligned} \left( \rho +\frac{2}{\varepsilon }\right) v^{\varepsilon }(p,{\bar{x}}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}) -\left( f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\right) (p,{\bar{x}}) -Qv^{\varepsilon }(\cdot ,{\bar{x}})(p)\ge 0. \end{aligned} \end{aligned}$$

This leads to the desired viscosity supersolution property.

Viscosity subsolution property. We argue by contradiction. If it were not, from the continuity of $v^{\varepsilon }$, there would exist ${\bar{p}}$, ${\bar{x}}$, a constant $\delta >0$, and a function $\varphi \in C^{2}$ such that $v^{\varepsilon }_{{\bar{p}}}(x)-\varphi (x)$ attains its maximum at ${\bar{x}}$ in the neighborhood $B_{\delta }({\bar{x}})=({\bar{x}}-\delta ,{\bar{x}}+\delta )$, but, in $B_{\delta }({\bar{x}})$, we have

$$\begin{aligned} \begin{aligned} \left( \rho +\frac{2}{\varepsilon }\right) v^{\varepsilon }_{{\bar{p}}}({{x}}) -{\mathcal {L}}_{{\bar{p}}}\varphi ({{x}}) -\left( f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\right) ({\bar{p}},{{x}}) -Qv^{\varepsilon }(\cdot ,{{x}})({\bar{p}})\ge \delta . \end{aligned}\nonumber \\ \end{aligned}$$

(10)

Let $\tau _{\delta }=\inf \{t\ge 0: X^{{\bar{p}},{\bar{x}}}(t)\notin B_{\delta }({\bar{x}})\}$. Choose $\theta =\tau _{\alpha }\wedge \tau _{\delta }$ and define $\psi :{\mathcal {M}}\times R\rightarrow R$ as (9).

As in the proof of the viscosity supersolution property, applying Itô’s formula for $\psi$ between 0 and $\theta$, noting that $X^{{\bar{p}},{\bar{x}}}(t)\in B_{\delta }({\bar{x}})$ for $0\le t\le \theta$, and by the definition of $\varphi$, we arrive at

$$\begin{aligned} \begin{aligned}&E\bigg [e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta } v^{\varepsilon }(\alpha ^{{\bar{p}}}(\theta ),X^{{\bar{p}},{\bar{x}}}(\theta ))\bigg ] -v^{\varepsilon }({\bar{p}},{\bar{x}})\\&\quad \le E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) v^{\varepsilon }({\bar{p}},X^{{\bar{p}},{\bar{x}}}(t)) +{\mathcal {L}}_{{\bar{p}}}\varphi (X^{{\bar{p}},{\bar{x}}}(t))\\&\qquad +Qv^{\varepsilon }(\cdot ,X^{{\bar{p}},{\bar{x}}}(t))({\bar{p}})\bigg )dt\bigg ]. \end{aligned} \end{aligned}$$

(11)

Combining (10) and (11), we have

$$\begin{aligned} \begin{aligned} v^{\varepsilon }({\bar{p}},{\bar{x}})&\ge E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )({\bar{p}},X^{{\bar{p}},{\bar{x}}}(t))dt\\&\quad +e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )\theta } v^{\varepsilon }(\alpha ^{{\bar{p}}}(\theta ),X^{{\bar{p}},{\bar{x}}}(\theta ))\bigg ] +\delta E\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t}dt. \end{aligned} \end{aligned}$$

(12)

We now claim that there exists some positive constant $c_{0}$ such that

$$\begin{aligned} E\int _{0}^{\theta }e^{-\left( \rho +\frac{2}{\varepsilon }\right) t}dt\ge c_{0}. \end{aligned}$$

To this end, we take a smooth function $\phi (x)=c_{1}\left( 1-\frac{|x-{\bar{x}}|^{2}}{\delta ^{2}}\right)$ with

$$\begin{aligned} \begin{aligned} 0<c_{1}=\min \bigg \{1,\bigg (\rho +\frac{2}{\varepsilon } +\frac{2}{\delta }\max _{p\in {\mathcal {M}}}\sup _{x\in B_{\delta }({\bar{x}})}|b| +\frac{1}{\delta ^{2}}\max _{p\in {\mathcal {M}}}\sup _{x\in B_{\delta }({\bar{x}})} \sigma ^{2}\bigg )^{-1}\bigg \}. \end{aligned} \end{aligned}$$

By applying Itô’s formula to $e^{-(\rho +\frac{2}{\varepsilon }) t} \phi (X^{{\bar{p}},{\bar{x}}}(t))$ between 0 and $\theta$, we have

$$\begin{aligned} \begin{aligned} c_{1}&=\phi ({\bar{x}}) =E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (\bigg (\rho +\frac{2}{\varepsilon }\bigg )\phi (X^{{\bar{p}},{\bar{x}}}(t)) -{\mathcal {L}}_{{\bar{p}}}\phi (X^{{\bar{p}},{\bar{x}}}(t))\bigg )dt\\&\quad +e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta }\phi (X^{{\bar{p}},{\bar{x}}}(\theta ))\bigg ]\\&\le E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t}dt +e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) \theta }\phi (X^{{\bar{p}},{\bar{x}}}(\theta ))\bigg ]. \end{aligned} \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned}&E\left[ e^{-\left( \rho +\frac{2}{\varepsilon }\right) \theta } \phi (X^{{\bar{p}},{\bar{x}}}(\theta ))\right] \\&\quad =E\left[ e^{-\left( \rho +\frac{2}{\varepsilon }\right) \theta } \phi (X^{{\bar{p}},{\bar{x}}}(\theta )) (1_{\{\tau _{\alpha }<\tau _{\delta }\}} +1_{\{\tau _{\alpha }\ge \tau _{\delta }\}})\right] \\&\quad =E\left[ e^{-\left( \rho +\frac{2}{\varepsilon }\right) \tau _{\alpha }}\phi (X^{{\bar{p}},{\bar{x}}}(\tau _{\alpha }))\right] . \end{aligned} \end{aligned}$$

Since $\tau _{\alpha }$ is the first jump time of the Markov chain, so $\tau _{\alpha }>0$, a.s., then

$$\begin{aligned} \begin{aligned} E\left[ e^{-\left( \rho +\frac{2}{\varepsilon }\right) \tau _{\alpha }}\phi (X^{{\bar{p}},{\bar{x}}}(\tau _{\alpha }))\right] \doteq c_{2}<c_{1}. \end{aligned} \end{aligned}$$

Denote $c_{0}=c_{1}-c_{2}>0$, we have

$$\begin{aligned} \begin{aligned} E\int _{0}^{\theta }e^{-\left( \rho +\frac{2}{\varepsilon }\right) t}dt \ge c_{1}-c_{2}=c_{0}>0. \end{aligned} \end{aligned}$$

This proves the claim. Going back to (12), we obtain

$$\begin{aligned} \begin{aligned}&v^{\varepsilon }({\bar{p}},{\bar{x}}) \ge E\bigg [\int _{0}^{\theta }e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg ) t} \bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }\vee h\bigg )({\bar{p}},X^{{\bar{p}},{\bar{x}}}(t))dt\\&\quad +e^{-\bigg (\rho +\frac{2}{\varepsilon }\bigg )\theta } v^{\varepsilon }(\alpha ^{{\bar{p}}}(\theta ),X^{{\bar{p}},{\bar{x}}}(\theta ))\bigg ]+\delta c_{0}, \end{aligned} \end{aligned}$$

which is in contradiction with (5). Therefore, $v^{\varepsilon }$ is a viscosity subsolution.

Consequently, $v^{\varepsilon }$ is a viscosity solution of the penalized HJB Eq. (6). $\square$

The following theorem gives the uniqueness result of the viscosity solution of (6), which is proved by noting that a viscosity solution is both a viscosity subsolution and a viscosity supersolution.

Theorem 2

Assume (A1)–(A3). Then, (6) has at most one viscosity solution in ${\mathcal {A}}$.

Proof

Let $v^{\varepsilon }_{1}$ and $v^{\varepsilon }_{2}\in {\mathcal {A}}$ be two viscosity solutions of (6). We claim $v^{\varepsilon }_{1}\le v^{\varepsilon }_{2}$. If not, suppose there exists $({\bar{p}},{\bar{x}})\in {\mathcal {M}}\times R$ such that $v^{\varepsilon }_{1}({\bar{p}},{\bar{x}})-v^{\varepsilon }_{2}({\bar{p}},{\bar{x}})>0$, which implies $v^{\varepsilon }_{1}({\bar{p}},{\bar{x}})-v^{\varepsilon }_{2}({\bar{p}},{\bar{x}})\ge \kappa$, for some $\kappa >0$.

For any $0<\delta <1$ and $0<\gamma <1$, consider a function defined on ${\mathcal {M}}\times R\times R$:

$$\begin{aligned} \begin{aligned} {\varPsi }(p,x_{1},x_{2}) =v^{\varepsilon }_{1}(p,x_{1}) -v^{\varepsilon }_{2}(p,x_{2}) -\frac{1}{2\delta }|x_{1}-x_{2}|^{2} -\gamma (\psi (x_{1})+\psi (x_{2})), \end{aligned} \end{aligned}$$

(13)

where $\psi (x)=\frac{1}{2}\log (1+|x|^{2})$. It is easy to see that ${\varPsi }(p,x_{1},x_{2})$ has a global maximum at a point $(p_{0},x^{0}_{1},x^{0}_{2})$, since ${\varPsi }(p,\cdot ,\cdot )$ is continuous and $\lim _{|x_{1}|+|x_{2}|\rightarrow \infty }{\varPsi }=-\infty$, for each $p\in {\mathcal {M}}$. In particular,

$$\begin{aligned} \begin{aligned} {\varPsi }(p_{0},x^{0}_{1},x^{0}_{2}) \ge {\varPsi }({\bar{p}},{\bar{x}},{\bar{x}}) =v^{\varepsilon }_{1}({\bar{p}},{\bar{x}}) -v^{\varepsilon }_{2}({\bar{p}},{\bar{x}}) -2\gamma \psi ({\bar{x}}) \ge \kappa -2\gamma \psi ({\bar{x}}) \ge \frac{\kappa }{2}, \end{aligned} \end{aligned}$$

for sufficiently small $\gamma$. That is,

$$\begin{aligned} \begin{aligned} \frac{\kappa }{2} \le&v^{\varepsilon }_{1}(p_{0},x^{0}_{1}) -v^{\varepsilon }_{2}(p_{0},x^{0}_{2}) -\frac{1}{2\delta }|x^{0}_{1}-x^{0}_{2}|^{2} -\gamma (\psi (x^{0}_{1})+\psi (x^{0}_{2}))\\ \le&v^{\varepsilon }_{1}(p_{0},x^{0}_{1}) -v^{\varepsilon }_{2}(p_{0},x^{0}_{2}). \end{aligned} \end{aligned}$$

(14)

Besides, by the definition of $(p_{0},x_{1}^{0},x_{2}^{0})$, we have $2{\varPsi }(p_{0},x^{0}_{1},x^{0}_{2})\ge {\varPsi }(p_{0},x^{0}_{1},x^{0}_{1}) +{\varPsi }(p_{0},x^{0}_{2},x^{0}_{2})$, i.e.,

$$\begin{aligned} \begin{aligned} \frac{1}{\delta }|x_{1}^{0}-x_{2}^{0}|^{2} \le (v^{\varepsilon }_{1}(p_{0},x_{1}^{0}) -v^{\varepsilon }_{1}(p_{0},x_{2}^{0})) +(v^{\varepsilon }_{2}(p_{0},x_{1}^{0}) -v^{\varepsilon }_{2}(p_{0},x_{2}^{0})). \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} |x_{1}^{0}-x_{2}^{0}|\le \sqrt{K\delta }. \end{aligned} \end{aligned}$$

(15)

From the uniform continuity of $v^{\varepsilon }_{i}$, $i=1,2$, we also deduce that

$$\begin{aligned} \begin{aligned} \frac{|x_{1}^{0}-x_{2}^{0}|^{2}}{\delta }\rightarrow 0, \quad \delta \rightarrow 0. \end{aligned} \end{aligned}$$

Moreover, the choice of $(p_{0},x_{1}^{0},x_{2}^{0})$ implies ${\varPsi }(p_{0},0,0)\le {\varPsi }(p_{0},x^{0}_{1},x^{0}_{2})$, which yields

$$\begin{aligned} \begin{aligned} \gamma (\psi (x^{0}_{1})+\psi (x^{0}_{2})) \le v^{\varepsilon }_{1}(p_{0},x^{0}_{1}) -v^{\varepsilon }_{2}(p_{0},x^{0}_{2}) -\frac{1}{2\delta }|x^{0}_{1}-x^{0}_{2}|^{2} -{\varPsi }(p_{0},0,0)\le K. \end{aligned} \end{aligned}$$

Therefore, there exists a constant $K_{\gamma }$ (independent of $\delta$) such that

$$\begin{aligned} \begin{aligned} |x_{1}^{0}|+|x_{2}^{0}|\le K_{\gamma }. \end{aligned} \end{aligned}$$

(16)

In view of (15) and (16), there exists a subsequence of $\delta \rightarrow 0$ (still denoted by $\delta$) and $x_{0}$ such that $x_{1}^{0}\rightarrow x_{0}$ and $x_{2}^{0}\rightarrow x_{0}$. So letting $\delta \rightarrow 0$ in (14), we have

$$\begin{aligned} \begin{aligned} \frac{\kappa }{2} \le v^{\varepsilon }_{1}(p_{0},x_{0}) -v^{\varepsilon }_{2}(p_{0},x_{0}). \end{aligned} \end{aligned}$$

(17)

On the other hand, applying Theorem 3.2 in Crandall et al. (1992), there exist ${\varLambda }_{1}$ and ${\varLambda }_{2}$ such that

$$\begin{aligned} \begin{aligned} \bigg (\frac{x_{1}^{0}-x_{2}^{0}}{\delta },{\varLambda }_{1}\bigg ) \in&{\bar{J}}^{2,+}(v^{\varepsilon }_{1}(p_{0},x^{0}_{1}) -\gamma \psi (x^{0}_{1})),\\ \bigg (\frac{x_{1}^{0}-x_{2}^{0}}{\delta },{\varLambda }_{2}\bigg ) \in&{\bar{J}}^{2,-}(v^{\varepsilon }_{2}(p_{0},x^{0}_{2}) +\gamma \psi (x^{0}_{2})), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \left( \begin{array}{cc} {\varLambda }_{1} &{} 0 \\ 0 &{} -{\varLambda }_{2} \\ \end{array} \right) \le \frac{3}{\delta } \left( \begin{array}{ll} 1 &{} -\,1 \\ -\,1 &{} 1 \\ \end{array} \right) . \end{aligned} \end{aligned}$$

It follows immediately that

$$\begin{aligned} \sigma ^{2}(p_{0},x_{1}^{0}){\varLambda }_{1}-\sigma ^{2}(p_{0},x_{2}^{0}){\varLambda }_{2} \le \frac{3}{\delta }|\sigma (p_{0},x_{1}^{0})-\sigma (p_{0},x_{2}^{0})|^{2}. \end{aligned}$$

By writing the viscosity subsolution property of $v^{\varepsilon }_{1}(p,x)$ and the viscosity supersolution property of $v^{\varepsilon }_{2}(p,x)$ (noting Remark 1), we have

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{2}{\varepsilon }\bigg )v^{\varepsilon }_{1}(p_{0},x_{1}^{0})\\&\quad \le b(p_{0},x_{1}^{0})\bigg (\frac{x_{1}^{0}-x_{2}^{0}}{\delta }+\gamma \frac{\partial \psi }{\partial x}(x_{1}^{0})\bigg ) +\frac{\sigma ^{2}(p_{0},x_{1}^{0})}{2}\bigg ({\varLambda }_{1}+\gamma \frac{\partial ^{2} \psi }{\partial x^{2}}(x_{1}^{0})\bigg )\\&\qquad +\bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }_{1}\wedge g+\frac{1}{\varepsilon }v^{\varepsilon }_{1}\vee h\bigg )(p_{0},x_{1}^{0}) +Qv^{\varepsilon }_{1}(\cdot ,x_{1}^{0})(p_{0}) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{2}{\varepsilon }\bigg )v^{\varepsilon }_{2}(p_{0},x_{2}^{0})\\&\quad \ge b(p_{0},x_{2}^{0})\bigg (\frac{x_{1}^{0}-x_{2}^{0}}{\delta }-\gamma \frac{\partial \psi }{\partial x}(x_{2}^{0})\bigg ) +\frac{\sigma ^{2}(p_{0},x_{2}^{0})}{2}\bigg ({\varLambda }_{2}- \gamma \frac{\partial ^{2} \psi }{\partial x^{2}}(x_{2}^{0})\bigg )\\&\qquad +\bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }_{2}\wedge g+\frac{1}{\varepsilon }v^{\varepsilon }_{2}\vee h\bigg )(p_{0},x_{2}^{0}) +Qv^{\varepsilon }_{2}(\cdot ,x_{2}^{0})(p_{0}), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \frac{\partial }{\partial x}\psi (x) =\frac{x}{1+|x|^{2}}, \quad \frac{\partial ^{2}}{\partial x^{2}} \psi (x)=\frac{1-|x|^{2}}{(1+|x|^{2})^{2}} \end{aligned}$$

are bounded by 1.

From the above two inequalities, we have

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{2}{\varepsilon }\bigg )(v^{\varepsilon }_{1}(p_{0},x_{1}^{0})- v^{\varepsilon }_{2}(p_{0},x_{2}^{0}))\\&\quad \le \bigg (b(p_{0},x_{1}^{0})-b(p_{0},x_{2}^{0})\bigg ) \frac{x_{1}^{0}-x_{2}^{0}}{\delta } \\&\qquad +\gamma \bigg (b(p_{0},x_{1}^{0})\frac{\partial }{\partial x}\psi (x_{1}^{0}) +b(p_{0},x_{2}^{0})\frac{\partial }{\partial x}\psi (x_{2}^{0})\bigg )\\&\qquad +\frac{1}{2}\bigg (\sigma ^{2}(p_{0},x_{1}^{0}){\varLambda }_{1}- \sigma ^{2}(p_{0},x_{2}^{0}){\varLambda }_{2}\bigg )\\&\qquad +\frac{\gamma }{2}\bigg (\sigma ^{2}(p_{0},x_{1}^{0}) \frac{\partial ^{2}}{\partial x^{2}}\psi (x_{1}^{0}) +\sigma ^{2}(p_{0},x_{2}^{0})\frac{\partial ^{2}}{\partial x^{2}}\psi (x_{2}^{0})\bigg )\\&\qquad +\bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }_{1}\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }_{1}\vee h\bigg )(p_{0},x_{1}^{0}) -\bigg (f+\frac{1}{\varepsilon }v^{\varepsilon }_{2}\wedge g +\frac{1}{\varepsilon }v^{\varepsilon }_{2}\vee h\bigg )(p_{0},x_{2}^{0})\\&\qquad +Qv^{\varepsilon }_{1}(\cdot ,x_{1}^{0})(p_{0})- Qv^{\varepsilon }_{2}(\cdot ,x_{2}^{0})(p_{0}). \end{aligned} \end{aligned}$$

Letting $\delta \rightarrow 0$, we have

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{2}{\varepsilon }\bigg )(v^{\varepsilon }_{1}(p_{0},x_{0})- v^{\varepsilon }_{2}(p_{0},x_{0}))\\&\quad \le \gamma \bigg (b(p_{0},x_{0})\frac{\partial }{\partial x}\psi (x_{0}) +b(p_{0},x_{0})\frac{\partial }{\partial x}\psi (x_{0})\bigg )\\&\qquad +\frac{\gamma }{2}\bigg (\sigma ^{2}(p_{0},x_{0}) \frac{\partial ^{2}}{\partial x^{2}}\psi (x_{0}) +\sigma ^{2}(p_{0},x_{0})\frac{\partial ^{2}}{\partial x^{2}}\psi (x_{0})\bigg )\\&\qquad +Qv^{\varepsilon }_{1}(\cdot ,x_{0})(p_{0})- Qv^{\varepsilon }_{2}(\cdot ,x_{0})(p_{0}). \end{aligned} \end{aligned}$$

(18)

Since ${\varPsi }(p,x_{1},x_{2})$ reaches a maximum at $(p_{0},x_{1}^{0},x_{2}^{0})$, it follows that for all x and all $q\in {\mathcal {M}}$,

$$\begin{aligned} \begin{aligned} v^{\varepsilon }_{1}(q,x)-v^{\varepsilon }_{2}(q,x) -2\gamma \psi (x) =&{\varPsi }(q,x,x)\\ \le&{\varPsi }(p_{0},x^{0}_{1},x^{0}_{2})\\ \le&v^{\varepsilon }_{1}(p_{0},x^{0}_{1})-v^{\varepsilon }_{2}(p_{0},x^{0}_{2}) -\gamma (\psi (x^{0}_{1})+\psi (x^{0}_{2})). \end{aligned} \end{aligned}$$

Again, letting $\delta \rightarrow 0$, and recalling that $x_{1}^{0}\rightarrow x_{0}$ and $x_{2}^{0}\rightarrow x_{0}$,

$$\begin{aligned} \begin{aligned} v^{\varepsilon }_{1}(q,x)-v^{\varepsilon }_{2}(q,x)-2\gamma \psi (x) \le v^{\varepsilon }_{1}(p_{0},x_{0})-v^{\varepsilon }_{2}(p_{0},x_{0})-2\gamma \psi (x_{0}). \end{aligned} \end{aligned}$$

In particular, taking $x=x_{0}$ leads to

$$\begin{aligned} v^{\varepsilon }_{1}(q,x_{0})-v^{\varepsilon }_{2}(q,x_{0}) \le v^{\varepsilon }_{1}(p_{0},x_{0})-v^{\varepsilon }_{2}(p_{0},x_{0}). \end{aligned}$$

Hence we have

$$\begin{aligned} \begin{aligned}&Qv^{\varepsilon }_{1}(\cdot ,x_{0})(p_{0}) -Qv^{\varepsilon }_{2}(\cdot ,x_{0})(p_{0})\\&\quad =\sum _{q\ne p_{0}}\lambda _{p_{0}q} [(v^{\varepsilon }_{1}(q,x_{0}) -v^{\varepsilon }_{1}(p_{0},x_{0})) -(v^{\varepsilon }_{2}(q,x_{0}) -v^{\varepsilon }_{2}(p_{0},x_{0}))]\\&\quad =\sum _{q\ne p_{0}}\lambda _{p_{0}q} [(v^{\varepsilon }_{1}(q,x_{0})-v^{\varepsilon }_{2}(q,x_{0})) -(v^{\varepsilon }_{1}(p_{0},x_{0})-v^{\varepsilon }_{2}(p_{0},x_{0}))] \le 0. \end{aligned} \end{aligned}$$

(19)

In view of (18) and (19), we obtain

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{2}{\varepsilon }\bigg )(v^{\varepsilon }_{1}(p_{0},x_{0}) -v^{\varepsilon }_{2}(p_{0},x_{0}))\\&\quad \le \gamma \bigg (b(p_{0},x_{0})\frac{\partial }{\partial x}\psi (x_{0}) +b(p_{0},x_{0})\frac{\partial }{\partial x}\psi (x_{0})\bigg )\\&\qquad +\frac{\gamma }{2}\bigg (\sigma ^{2}(p_{0},x_{0}) \frac{\partial ^{2}}{\partial x^{2}}\psi (x_{0}) +\sigma ^{2}(p_{0},x_{0})\frac{\partial ^{2}}{\partial x^{2}}\psi (x_{0})\bigg ). \end{aligned} \end{aligned}$$

Letting $\gamma \rightarrow 0$, we arrive at $v^{\varepsilon }_{1}(p_{0},x_{0})- v^{\varepsilon }_{2}(p_{0},x_{0})\le 0$, which is a contradiction with (17). $\square$

Remark 2

Note that (6) can be also rewritten as the following form:

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{1}{\varepsilon }1_{\{v^{\varepsilon }\ge g\}} +\frac{1}{\varepsilon }1_{\{v^{\varepsilon }< h\}}\bigg )v^{\varepsilon }_{p}(x)\\&\quad - {\mathcal {L}}_{p}v^{\varepsilon }_{p}(x)-\bigg (f+\frac{1}{\varepsilon } 1_{\{v^{\varepsilon }\ge g\}}g+\frac{1}{\varepsilon }1_{\{v^{\varepsilon }< h\}}h\bigg )(p,x) -Qv^{\varepsilon }(\cdot ,x)(p)=0, \end{aligned} \end{aligned}$$

we derive that $v^{\varepsilon }(p,x)$ has another representation:

$$\begin{aligned} \begin{aligned} v^{\varepsilon }(p,x)&=E\int _{0}^{\infty }e^{-\bigg (\rho +\frac{1}{\varepsilon }1_{\{v^{\varepsilon }\ge g\}} +\frac{1}{\varepsilon }1_{\{v^{\varepsilon }< h\}}\bigg ) t}\\&\quad \times \bigg (f+\frac{1}{\varepsilon }1_{\{v^{\varepsilon }\ge g\}}g+\frac{1}{\varepsilon }1_{\{v^{\varepsilon }< h\}}h\bigg ) (\alpha ^{p}(t),X^{p,x}(t))dt. \end{aligned} \end{aligned}$$

Corollary 1

Assume (A1)–(A3). Then, for any $(p,x)\in {\mathcal {M}}\times R$, we have

$$\begin{aligned} \begin{aligned} v^{\varepsilon }(p,x)=\inf _{\tau _{1}}\sup _{\tau _{2}} G(\tau _{1},\tau _{2})=\sup _{\tau _{2}}\inf _{\tau _{1}} G(\tau _{1},\tau _{2})=G({\hat{\tau }}_{1},{\hat{\tau }}_{2}), \end{aligned} \end{aligned}$$

where ${\hat{\tau }}_{1}=\inf \{t\ge 0:v^{\varepsilon }\ge g\}$, ${\hat{\tau }}_{2}=\inf \{t\ge 0:v^{\varepsilon }\le h\}$, and

$$\begin{aligned} \begin{aligned} G(\tau _{1},\tau _{2})&=E\bigg \{\int _{0}^{\tau _{1}\wedge \tau _{2}}e^{-\rho t}f(\alpha ^{p}(t),X^{p,x}(t))dt\\&\qquad +e^{-\rho (\tau _{1}\wedge \tau _{2})} \bigg ([g+(v^{\varepsilon }-g)^{+}](\alpha ^{p}(\tau _{1}), X^{p,x}(\tau _{1}))1_{\{\tau _{1}<\tau _{2}\}}\\&\qquad +[h-(v^{\varepsilon }-h)^{-}](\alpha ^{p}(\tau _{2}), X^{p,x}(\tau _{2}))1_{\{\tau _{1}\ge \tau _{2}\}}\bigg )\bigg \}. \end{aligned} \end{aligned}$$

Proof

Only a sketch of the proof is given here. In view of the form of penalized HJB equation (7), we can write the corresponding “control problem” and then the dynamic programming principle. The desired conclusion follows if we observe that $(v^{\varepsilon }-g)^{+}=0$ for $t<{\hat{\tau }}_{1}$ and $v^{\varepsilon }=v^{\varepsilon }\vee g$ at ${\hat{\tau }}_{1}$, as well as $(v^{\varepsilon }-h)^{-}=0$ for $t<{\hat{\tau }}_{2}$ and $v^{\varepsilon }=v^{\varepsilon }\wedge h$ at ${\hat{\tau }}_{2}$. $\square$

3 Original problem

In this section, we show that the unique viscosity solution of (6), or simply the value function of penalized problem defined by (4) converges to the unique viscosity solution of variational inequalities (3), as $\varepsilon :=\varepsilon _{n}=2^{-n}\rightarrow 0$, which is exactly the value of the Dynkin game. To this end, define

$$\begin{aligned} \begin{aligned} G_{\beta }\varphi (p,x)=E\int _{0}^{\infty }e^{-\beta t} \varphi (\alpha ^{p}(t),X^{p,x}(t))dt,\quad \beta >0, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\mathcal {B}}=\{G_{\beta }(\beta \varphi ): \varphi \in {\mathcal {A}}, \beta >\rho \}. \end{aligned} \end{aligned}$$

Obviously, ${\mathcal {B}}\subset {\mathcal {A}}$. Further, the next lemma gives the density of ${\mathcal {B}}$ in ${\mathcal {A}}$, whose proof follows that for any $\varphi \in {\mathcal {A}}$, the sequence $\{G_{\beta }(\beta \varphi )\}\subset {\mathcal {B}}$ satisfies $\Vert G_{\beta }(\beta \varphi )-\varphi \Vert \rightarrow 0$ as $\beta \rightarrow \infty$.

Lemma 3

Under assumptions (A1)–(A3), ${\mathcal {B}}$ is dense in ${\mathcal {A}}$.

The following two lemmas are concerned with the stability and the range of $v^{\varepsilon }$, respectively. Lemma 4 can be proved by making use of a Picard-type iteration method introduced in Bensoussan (1982, Lemma 5.5).

Lemma 4

Under assumptions (A1)–(A3), let $v^{\varepsilon }_{i}$ be the solution of (4) corresponding to $g_{i}$ and $h_{i}\in {\mathcal {A}}$, $i=1,2$, then we have

$$\begin{aligned} \begin{aligned} \Vert v^{\varepsilon }_{1}-v^{\varepsilon }_{2}\Vert \le \Vert g_{1}-g_{2}\Vert +\Vert h_{1}-h_{2}\Vert . \end{aligned} \end{aligned}$$

Lemma 5

Under assumptions (A1)–(A3), for any g and $h\in {\mathcal {B}}$, there exists a constant $K>0$, independent of $\varepsilon$, such that

$$\begin{aligned} \begin{aligned} (v^{\varepsilon }-g)^{+}(p,x)+(v^{\varepsilon }-h)^{-}(p,x) \le K \varepsilon . \end{aligned} \end{aligned}$$

(20)

Proof

Let $g=G_{\beta }(\beta \varphi )\in {\mathcal {B}}$ for some $\varphi \in {\mathcal {A}}$. As the proofs of Theorems 1 and 2, it turns out that g is the unique viscosity solution of

$$\begin{aligned} \begin{aligned} \beta g-{\mathcal {L}}_{p}g-\beta \varphi -Qg(\cdot ,x)(p)=0, \end{aligned} \end{aligned}$$

or equivalently,

$$\begin{aligned} \begin{aligned} \left( \rho +\frac{2}{\varepsilon }\right) g-{\mathcal {L}}_{p}g -\left( {\tilde{\varphi }}+\frac{2}{\varepsilon }g\right) -Qg(\cdot ,x)(p)=0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\tilde{\varphi }}=(\rho -\beta )g+\beta \varphi \in {\mathcal {A}}. \end{aligned}$$

Compared with the expression of $v^{\varepsilon }$ in Remark 2, we rewrite the above equation as

$$\begin{aligned} \begin{aligned}&\bigg (\rho +\frac{1}{\varepsilon }1_{\{v\ge g\}} +\frac{1}{\varepsilon }1_{\{v< h\}}\bigg )g -{\mathcal {L}}_{p}g -\bigg ({\tilde{\varphi }} +\frac{1}{\varepsilon }1_{\{v\ge g\}}g+ \frac{1}{\varepsilon }1_{\{v< h\}}g\bigg )\\&\quad -Qg(\cdot ,x)(p)=0. \end{aligned} \end{aligned}$$

This implies that g admits another representation:

$$\begin{aligned} \begin{aligned} g(p,x)&=E\int _{0}^{\infty } e^{-\bigg (\rho +\frac{1}{\varepsilon }1_{\{v\ge g\}} +\frac{1}{\varepsilon }1_{\{v< h\}}\bigg ) t} \\&\quad \bigg ({\tilde{\varphi }} +\frac{1}{\varepsilon }1_{\{v\ge g\}}g+\frac{1}{\varepsilon }1_{\{v< h\}}g\bigg )(\alpha ^{p}(t),X^{p,x}(t))dt. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned}&v^{\varepsilon }(p,x)-g(p,x)\\&\quad =E\int _{0}^{\infty }e^{-\bigg (\rho +\frac{1}{\varepsilon }1_{\{v\ge g\}} +\frac{1}{\varepsilon }1_{\{v< h\}}\bigg ) t}\bigg (f-{\tilde{\varphi }} +\frac{1}{\varepsilon }1_{\{v< h\}}(h-g)\bigg )(\alpha ^{p}(t),X^{p,x}(t))dt\\&\quad \le E\int _{0}^{\infty }e^{-\bigg (\rho +\frac{1}{\varepsilon }1_{\{v\ge g\}}+\frac{1}{\varepsilon }1_{\{v< h\}}\bigg ) t}(f-{\tilde{\varphi }})(\alpha ^{p}(t),X^{p,x}(t))dt\\&\quad \le \frac{\varepsilon }{\rho \varepsilon +2}\Vert f-{\tilde{\varphi }}\Vert . \end{aligned} \end{aligned}$$

Similarly, for $h\in {\mathcal {B}}$, we can find a ${\tilde{\psi }}\in {\mathcal {A}}$ such that

$$\begin{aligned} v^{\varepsilon }-h \ge -\frac{\varepsilon }{\rho \varepsilon +2}\Vert f-{\tilde{\psi }}\Vert . \end{aligned}$$

Hence, we have

$$\begin{aligned} \begin{aligned} (v^{\varepsilon }-g)^{+}(p,x)+(v^{\varepsilon }-h)^{-}(p,x) \le \frac{\varepsilon }{\rho \varepsilon +2}(\Vert f-{\tilde{\varphi }}\Vert +\Vert f-{\tilde{\psi }}\Vert ). \end{aligned} \end{aligned}$$

Taking $K=\frac{\Vert f-{\tilde{\varphi }}\Vert +\Vert f-{\tilde{\psi }}\Vert }{2}$ completes the proof. $\square$

Theorem 3

Under assumptions (A1)–(A3). Then, we have $v^{\varepsilon }\rightarrow v$ in norm as $\varepsilon \rightarrow 0$, for some $v\in {\mathcal {A}}$.

Proof

First, suppose g and $h\in {\mathcal {B}}$. In view of Corollary 1 and Lemma 5, we have

$$\begin{aligned} \begin{aligned}&|v^{\varepsilon _{n+1}}(p,x)-v^{\varepsilon _{n}}(p,x)|\\&\quad \le E\bigg [e^{-\rho (\tau _{1}\wedge \tau _{2})} \bigg (|(v^{\varepsilon _{n+1}}-g)^{+}-(v^{\varepsilon _{n}}-g)^{+}| (\alpha ^{p}(\tau _{1}),X^{p,x}(\tau _{1}))1_{\{\tau _{1}<\tau _{2}\}}\\&\qquad +|(v^{\varepsilon _{n+1}}-h)^{-} -(v^{\varepsilon _{n}}-h)^{-}(\alpha ^{p}(\tau _{2}),X^{p,x}(\tau _{2})) 1_{\{\tau _{1}\ge \tau _{2}\}}\bigg )\bigg ]\\&\quad \le K(\varepsilon _{n+1}+\varepsilon _{n}). \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \sum _{n=1}^{\infty }\Vert v^{\varepsilon _{n+1}}-v^{\varepsilon _{n}}\Vert \le \sum _{n=1}^{\infty }K(\varepsilon _{n+1}+\varepsilon _{n})<\infty . \end{aligned} \end{aligned}$$

It means that $v^{\varepsilon _{n}}$ is a Cauchy sequence in ${\mathcal {A}}$ and the desired convergence follows.

In the case g and $h\in {\mathcal {A}}$, there exist sequences $\{g_{m}\}$ and $\{h_{m}\}\subset {\mathcal {B}}$ such that $g_{m}\rightarrow g$ and $h_{m}\rightarrow h$, due to the density. Let $v^{\varepsilon _{n}}_{m}$ be the solution of (4) corresponding to $g_{m}$ and $h_{m}$. By the above argument, we see that $v^{\varepsilon _{n}}_{m}\rightarrow v_{m}$ for some $v_{m}\in {\mathcal {A}}$, as $n\rightarrow \infty$.

In view of Lemma 4, it follows that

$$\begin{aligned} \begin{aligned} \Vert v^{\varepsilon _{n}}_{m_{1}}-v^{\varepsilon _{n}}_{m_{2}}\Vert \le \Vert g_{m_{1}}-g_{m_{2}}\Vert +\Vert h_{m_{1}}-h_{m_{2}}\Vert . \end{aligned} \end{aligned}$$

Letting $n\rightarrow \infty$, we have

$$\begin{aligned} \begin{aligned} \Vert v_{m_{1}}-v_{m_{2}}\Vert \le \Vert g_{m_{1}}-g_{m_{2}}\Vert +\Vert h_{m_{1}}-h_{m_{2}}\Vert , \end{aligned} \end{aligned}$$

which implies that $v_{m}$ is a Cauchy sequence in ${\mathcal {A}}$ and hence $v_{m}\rightarrow v\in {\mathcal {A}}$. Then we have

$$\begin{aligned} \begin{aligned} \Vert v^{\varepsilon _{n}}-v\Vert \le&\Vert v^{\varepsilon _{n}}-v^{\varepsilon _{n}}_{m}\Vert +\Vert v^{\varepsilon _{n}}_{m}-v_{m}\Vert +\Vert v_{m}-v\Vert \\ \le&\Vert g-g_{m}\Vert +\Vert h-h_{m}\Vert +\Vert v^{\varepsilon _{n}}_{m}-v_{m}\Vert +\Vert v_{m}-v\Vert . \end{aligned} \end{aligned}$$

We complete the proof by sending $n\rightarrow \infty$ and $m\rightarrow \infty$. $\square$

We present the definition of viscosity solution of the variational inequalities (3), which is somewhat different from Definition 1 or the ordinary definition of viscosity solution in Crandall et al. (1992).

Definition 3

A function $v\in {\mathcal {A}}$ is said to be a viscosity solution of (3) if it satisfies the following conditions:

• (i) For any $(p,x)\in {\mathcal {M}}\times R$,

  $$\begin{aligned} \begin{aligned} h(p,x)\le v(p,x)\le g(p,x). \end{aligned} \end{aligned}$$

  (21)

• (ii) For any $p\in {\mathcal {M}}$,

  $$\begin{aligned} \begin{aligned} \bigg (\rho v_{p}({\bar{x}})-{\mathcal {L}}_{p}\varphi ({\bar{x}}) -f(p,{\bar{x}})-Qv(\cdot ,{\bar{x}})(p)\bigg )(v_{p}({\bar{x}})-h(p,{\bar{x}}))^{+}\le 0, \end{aligned} \end{aligned}$$

  (22)

  whenever $\varphi \in C^{2}$ and $v_{p}-\varphi$ has a (strict) local maximum at $x={\bar{x}}$.

• (iii) For any $p\in {\mathcal {M}}$,

  $$\begin{aligned} \begin{aligned} \bigg (\rho v_{p}({\bar{x}})-{\mathcal {L}}_{p}\varphi ({\bar{x}}) -f(p,{\bar{x}})-Qv(\cdot ,{\bar{x}})(p)\bigg )(v_{p}({\bar{x}})-g(p,{\bar{x}}))^{-}\ge 0, \end{aligned} \end{aligned}$$

  (23)

  whenever $\varphi \in C^{2}$ and $v_{p}-\varphi$ has a (strict) local minimum at $x={\bar{x}}$.

Analogous to Definition 2, we can give an equivalent definition of viscosity solution of (3) through the second order superdifferential $J^{2,+}v_{p}(x)$ and second order subdifferential $J^{2,-}v_{p}(x)$, whose closures are denoted by ${\bar{J}}^{2,+}v_{p}(x)$ and ${\bar{J}}^{2,-}v_{p}(x)$, respectively. In addition, Remark 1 continues to hold.

Now we are in a position to show the existence and uniqueness of viscosity solution of variational inequalities (3).

Theorem 4

Under assumptions (A1)–(A3). Then, the limit function v is a viscosity solution of (3).

Proof

First, letting $\varepsilon \rightarrow 0$ in (20), we obtain

$$\begin{aligned} h(p,x)\le v_{p}(x)\le g(p,x) \end{aligned}$$

and then (21) holds.

Next, take a function $\varphi \in C^{2}$ such that $v_{p}-\varphi$ has a strict local maximum at ${\bar{x}}$ in a neighborhood $B_{\delta }({\bar{x}})$. Choose ${\bar{x}}_{n}\in B_{\delta }({\bar{x}})$ such that

$$\begin{aligned} v^{\varepsilon _{n}}_{p}({\bar{x}}_{n})-\varphi ({\bar{x}}_{n}) =\max _{x\in B_{\delta }({\bar{x}})}\{v^{\varepsilon _{n}}_{p}(x)-\varphi (x)\}. \end{aligned}$$

Then it follows ${\bar{x}}_{n}\rightarrow {\bar{x}}$ as $n\rightarrow \infty$.

In view of the viscosity subsolution property of $v^{\varepsilon _{n}}$ and recalling the form (7) of penalized HJB equation,

$$\begin{aligned} \begin{aligned}&\rho v^{\varepsilon _{n}}_{p}({\bar{x}}_{n}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}_{n}) -\left( f-\frac{1}{\varepsilon }(v^{\varepsilon _{n}}-g)^{+} +\frac{1}{\varepsilon }(v^{\varepsilon _{n}}-h)^{-}\right) (p,{\bar{x}}_{n})\\&\quad -Qv^{\varepsilon _{n}}(\cdot ,{\bar{x}}_{n})(p) \le 0, \end{aligned} \end{aligned}$$

from which we have

$$\begin{aligned} \begin{aligned} \rho v^{\varepsilon _{n}}_{p}({\bar{x}}_{n}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}_{n}) -\left( f+\frac{1}{\varepsilon }(v^{\varepsilon _{n}}-h)^{-}\right) (p,{\bar{x}}_{n}) -Qv^{\varepsilon _{n}}(\cdot ,{\bar{x}}_{n})(p)\le 0. \end{aligned} \end{aligned}$$

Noting that $(v^{\varepsilon _{n}}-h)^{-} (v^{\varepsilon _{n}}-h)^{+}=0$, multiplying both sides by $(v^{\varepsilon _{n}}_{p}({\bar{x}}_{n}) -h(p,{\bar{x}}_{n}))^{+}$, we obtain

$$\begin{aligned} \begin{aligned} \bigg (\rho v^{\varepsilon _{n}}_{p}({\bar{x}}_{n}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}_{n}) -f(p,{\bar{x}}_{n}) -Qv^{\varepsilon _{n}}(\cdot ,{\bar{x}}_{n})(p)\bigg ) (v^{\varepsilon _{n}}_{p}({\bar{x}}_{n}) -h(p,{\bar{x}}_{n}))^{+}\le 0. \end{aligned} \end{aligned}$$

Letting $n\rightarrow \infty$,

$$\begin{aligned} \begin{aligned} \bigg (\rho v_{p}({\bar{x}}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}) -f(p,{\bar{x}})-Qv(\cdot ,{\bar{x}})(p)\bigg ) (v_{p}({\bar{x}})-h(p,{\bar{x}}))^{+}\le 0. \end{aligned} \end{aligned}$$

Then (22) holds. Using the same argument we can also derive that

$$\begin{aligned} \begin{aligned} \bigg (\rho v_{p}({\bar{x}}) -{\mathcal {L}}_{p}\varphi ({\bar{x}}) -f(p,{\bar{x}})-Qv(\cdot ,{\bar{x}})(p)\bigg ) (v_{p}({\bar{x}})-g(p,{\bar{x}}))^{-}\ge 0, \end{aligned} \end{aligned}$$

for $\varphi \in C^{2}$ and $v_{p}-\varphi$ has a strict local minimum at $x={\bar{x}}$, which proves (23). $\square$

Theorem 5

Under assumptions (A1)–(A3). Then, (3) has at most one viscosity solution in ${\mathcal {A}}$.

Proof

Let $v_{i}\in {\mathcal {A}}$, $i=1,2$, be two viscosity solutions of (3). We first claim that for any $p\in {\mathcal {M}}$ and for any $(\eta _{1},{\varLambda }_{1})\in {\bar{J}}^{2,+}v_{1}(p,x)$,

$$\begin{aligned} \begin{aligned}&\bigg (\rho v_{1}(p,x)-b(p,x)\eta _{1} -\frac{1}{2}\sigma ^{2}(p,x){\varLambda }_{1} -f(p,x)\\&\quad -Qv_{1}(\cdot ,x)(p)\bigg )(v_{1}(p,x)-v_{2}(p,x))^{+}\le 0, \end{aligned} \end{aligned}$$

or equivalently,

$$\begin{aligned} \begin{aligned} \bigg (\rho v_{1}(p,{\bar{x}})-{\mathcal {L}}_{p}\varphi ({\bar{x}}) -f(p,{\bar{x}})-Qv_{1}(\cdot ,{\bar{x}})(p)\bigg )(v_{1}(p,{\bar{x}}) -v_{2}(p,{\bar{x}}))^{+}\le 0, \end{aligned} \end{aligned}$$

where $\varphi \in C^{2}$ and ${\bar{x}}$ is the maximum point of $v_{1}(p,\cdot )-\varphi (\cdot )$.

In fact, if $v_{1}\le v_{2}$, then $(v_{1}-v_{2})^{+}=0$. Otherwise, we have $v_{1}>v_{2}\ge h$, so $(v_{1}-h)^{+}>0$. By (22), we derive that

$$\begin{aligned} \begin{aligned} \left( \rho +\frac{2}{\varepsilon }\right) v_{1}(p,{\bar{x}}) -{\mathcal {L}}_{p}v_{1}(p,{\bar{x}}) -f(p,{\bar{x}})-Qv_{1}(\cdot ,{\bar{x}})(p)\le 0. \end{aligned} \end{aligned}$$

Similarly, by (23), we have for any $p\in {\mathcal {M}}$ and for any $(\eta _{2},{\varLambda }_{2})\in {\bar{J}}^{2,-}v_{2}(p,x)$,

$$\begin{aligned} \begin{aligned}&\bigg (\rho v_{2}(p,x)-b(p,x)\eta _{2} -\frac{1}{2}\sigma ^{2}(p,x){\varLambda }_{2} -f(p,x)\\&\quad -Qv_{2}(\cdot ,x)(p)\bigg )(v_{2}(p,x)-v_{1}(p,x))^{-}\ge 0. \end{aligned} \end{aligned}$$

Now, we prove this theorem by using the approach of Theorem 2. Here, we only give the sketch of the proof. Suppose there exists $({\bar{p}},{\bar{x}})\in {\mathcal {M}}\times R$ such that $v_{1}({\bar{p}},{\bar{x}})-v_{2}({\bar{p}},{\bar{x}})>0$, which implies $v_{1}({\bar{p}},{\bar{x}})-v_{2}({\bar{p}},{\bar{x}})>\kappa$ for some $\kappa >0$. We define ${\varPsi }(p,x_{1},x_{2})$ as (13). Then the maximizer $(p_{0},x_{1}^{0},x_{2}^{0})$ of ${\varPsi }(p,x_{1},x_{2})$ satisfies

$$\begin{aligned} \begin{aligned} \frac{\kappa }{2}\le v_{1}(p_{0},x^{0}_{1})-v_{2}(p_{0},x^{0}_{2}), \end{aligned} \end{aligned}$$

(24)

for sufficiently small $\gamma$; see (14). It follows from (15) and the uniform continuity of $v_{2}$ that

$$\begin{aligned} \begin{aligned} v_{1}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{1}^{0}) =&v_{1}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{2}^{0}) -(v_{2}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{2}^{0}))\\ \ge&v_{1}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{2}^{0}) -|v_{2}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{2}^{0})|\\ \ge&\frac{\kappa }{2}-|v_{2}(p_{0},x_{1}^{0}) -v_{2}(p_{0},x_{2}^{0})|\\ \ge&\frac{\kappa }{4}, \end{aligned} \end{aligned}$$

for sufficiently small $\delta$, which yields $(v_{1}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{1}^{0}))^{+}>0$. Hence,

$$\begin{aligned} \begin{aligned} \rho v_{1}(p_{0},x_{1}^{0}) -b(p_{0},x_{1}^{0})\eta _{1} -\frac{1}{2}\sigma ^{2}(p_{0},x_{1}^{0}){\varLambda }_{1} -f(p_{0},x_{1}^{0}) -Qv_{1}(\cdot ,x_{1}^{0})(p_{0})\le 0, \end{aligned} \end{aligned}$$

for any $(\eta _{1},{\varLambda }_{1})\in {\bar{J}}^{2,+}v_{1}(p_{0},x_{1}^{0})$. In like manner,

$$\begin{aligned} \begin{aligned} \rho v_{2}(p_{0},x_{2}^{0}) -b(p_{0},x_{2}^{0})\eta _{2} -\frac{1}{2}\sigma ^{2}(p_{0},x_{2}^{0}){\varLambda }_{2} -f(p_{0},x_{2}^{0}) -Qv_{2}(\cdot ,x_{2}^{0})(p_{0})\ge 0, \end{aligned} \end{aligned}$$

for any $(\eta _{2},{\varLambda }_{2})\in {\bar{J}}^{2,-}v_{2}(p_{0},x_{2}^{0})$.

Combining the above two inequalities, by the same arguments as in Theorem 2, we have

$$\begin{aligned} \begin{aligned} \rho (v_{1}(p_{0},x_{1}^{0})-v_{2}(p_{0},x_{2}^{0}))\rightarrow 0, \end{aligned} \end{aligned}$$

as $\delta$ and $\gamma$ go to 0, which is contrary with (24). $\square$

Using the similar procedure of Morimoto (2003, Theorem 3.8), we give a stochastic interpretation of the viscosity solution v of variational inequalities (3), which implies that v is the value of the Dynkin game.

Theorem 6

Under assumptions (A1)–(A3), we have

$$\begin{aligned} \begin{aligned} v(p,x) =\inf _{\tau _{1}}\sup _{\tau _{2}}J(\tau _{1},\tau _{2}) =\sup _{\tau _{2}}\inf _{\tau _{1}}J(\tau _{1},\tau _{2}) =J(\tau _{1}^{*},\tau _{2}^{*}), \end{aligned} \end{aligned}$$

where $\tau _{1}^{*}=\inf \{t\ge 0:v\ge g\}$ and $\tau _{2}^{*}=\inf \{t\ge 0:v\le h\}$.

4 An application to game option

In this section, we consider a numerical example on pricing of game put option in a regime switching market (see Guo and Zhang 2004 for the pricing of American put option with regime switching).

To apply our results, we first cast the pricing problem of game option into the Dynkin game framework. Let $\alpha ^{p}(\cdot )$ be a Markov chain taking value in ${\mathcal {M}}=\{1,2\}$. Suppose the stock price is modeled by a switching geometric Brownian motion:

$$\begin{aligned} \left\{ \begin{aligned} dX^{p,x}(t)=&b(\alpha ^{p}(t))X^{p,x}(t)dt+ \sigma (\alpha ^{p}(t))X^{p,x}(t)dB(t),\quad t\ge 0,\\ X^{p,x}(0)=&x,\quad \alpha ^{p}(0)=p, \end{aligned} \right. \end{aligned}$$

where x and p are the initial values of the stock price and Markov chain, respectively. Here, b(p), $p\in {\mathcal {M}}$, is the expected return and $\sigma (p)$, $p\in {\mathcal {M}}$, represents the stock volatility.

In this example, $\alpha ^{p}(t)=1$ represents a bull market and $\alpha ^{p}(t)=2$ a bear market. We assume $b(1)>0$ and $b(2)<0$. In addition, the generator of $\alpha ^{p}(\cdot )$ is given by

$$\begin{aligned} \begin{aligned} \left( \begin{array}{cc} -\lambda _{1} &{} \lambda _{1} \\ \lambda _{2} &{} -\lambda _{2} \\ \end{array} \right) , \end{aligned} \end{aligned}$$

for some $\lambda _{1}>0$ and $\lambda _{2}>0$.

A game option is an American option with the following additional feature that the option can be terminated not only the buyer (by exercising), but also the seller (by cancelling). In particular, the buyer pays a premium (the fair price of the option) to the seller and has the right to exercise the option any time. When he decides to exercise the option at $\tau$, he receives the payment amount $h(X^{p,x}(\tau ))$ from the seller.

On the other hand, the seller is allowed to cancel the option any time. If she cancels the option at $\tau$, she pays the buyer the amount $g(X^{p,x}(\tau ))$. Naturally, we impose $g(X^{p,x}(\tau ))\ge h(X^{p,x}(\tau ))$, which means that in this case the amount the seller pays is equal to at least the one that the buyer would earn if he decides to exercise at $\tau$. The difference $(g-h)(X^{p,x}(\tau ))$ is the penalty that the seller pays for her decision to cancel the option. In addition, we take the convention that if the buyer exercises and the seller cancels at the same time $\tau$, then the seller pays to the buyer the amount $h(X^{p,x}(\tau ))$.

In a word, in the game option each player can choose a stopping time ($\tau =\tau _{1}$ by the seller and $\tau =\tau _{2}$ by the buyer, respectively), then at the time $\tau _{1}\wedge \tau _{2}$, the seller pays the amount

$$\begin{aligned} \begin{aligned} g(X^{p,x}(\tau _{1}))1_{\{\tau _{1}<\tau _{2}\}} +h(X^{p,x}(\tau _{2}))1_{\{\tau _{1}\ge \tau _{2}\}} \end{aligned} \end{aligned}$$

to the buyer. Given a discount factor $\rho$, the payoff of the option is denoted as

$$\begin{aligned} \begin{aligned} J(\tau _{1},\tau _{2}) =E\bigg [e^{-\rho (\tau _{1}\wedge \tau _{2})} \bigg (g(X^{p,x}(\tau _{1})) 1_{\{\tau _{1}<\tau _{2}\}} +h(X^{p,x}(\tau _{2})) 1_{\{\tau _{1}\ge \tau _{2}\}}\bigg )\bigg ]. \end{aligned} \end{aligned}$$

We want to find a saddle point $(\tau _{1}^{*},\tau _{2}^{*})$ for the buyer and the seller such that for any $(\tau _{1},\tau _{2})$,

$$\begin{aligned} J(\tau _{1}^{*},\tau _{2}) \le J(\tau _{1}^{*},\tau _{2}^{*}) \le J(\tau _{1},\tau _{2}^{*}), \end{aligned}$$

and we define the fair price of the option as

$$\begin{aligned} \begin{aligned} v(p,x) \doteq J(\tau _{1}^{*},\tau _{2}^{*}) =\inf _{\tau _{1}}\sup _{\tau _{2}}J(\tau _{1},\tau _{2}) =\sup _{\tau _{2}}\inf _{\tau _{1}}J(\tau _{1},\tau _{2}). \end{aligned} \end{aligned}$$

Clearly, the game option is a special case of the Dynkin game. The corresponding variational inequalities (3) becomes

$$\begin{aligned} \begin{aligned}&\min \bigg \{\max \bigg \{\rho v_{p}(x) -b(p)x\frac{\partial }{\partial x}v_{p}(x) -\frac{1}{2}\sigma ^{2}(p)x^{2} \frac{\partial ^{2}}{\partial x^{2}}v_{p}(x) -Qv(\cdot ,x)(p), \\&\qquad v_{p}(x)-g(p,x)\bigg \}, v_{p}(x)-h(p,x) \bigg \}=0. \end{aligned} \end{aligned}$$

(25)

Using this equation, we can compute the fair price as well as the optimal stopping rules for the buyer and the seller.

Remark 3

Given the above variational system, the stopping region is defined as

$$\begin{aligned} {\mathcal {S}}=\{x: v(p,x)\le h(p,x)\}\cup \{x: v(p,x)\ge g(p,x)\}. \end{aligned}$$

${\mathcal {S}}$ is a closed set and corresponds to the region where it is optimal to stop. The complement of ${\mathcal {S}}$, defined by

$$\begin{aligned} {\mathcal {C}}=\{x: h(p,x)< v(p,x)< g(p,x)\}, \end{aligned}$$

is the continuation region where one should remain the current situation; see Pham (2009) for more discussions on stopping and continuation regions.

Next, we focus on the numerical test. Let the functions h and g be given by

$$\begin{aligned} h(x)=(K-x)^{+},\quad g(x)=1.5(K-x)^{+}, \end{aligned}$$

where K is the strike price of the option.

We set the parameters in this example as $[b(1),b(2)]=[1,-1]$, $[\sigma ^{2}(1),\sigma ^{2}(2)]=[0.01,0.1]$, $[\lambda _{1},\lambda _{2}]=[24,24]$, $\rho =3$, $K=9$. We use a finite difference method to solve the variational inequalities (25) (the step size for x is chosen to be 0.001).

Here, $b(1)=1>0$ and $b(2)=-1<0$ represent the stock appreciation rates of up-trend and down-trend, respectively. The up-trend volatility $\sigma (1)=\sqrt{0.01}$, which is smaller than its down-trend counterpart $\sigma (2)=\sqrt{0.1}$. It is typical in marketplace because when a market trends up, investors are cautious and they move slowly, leading to a smaller volatility. On the other hand, during a sharp market downturn, the participants get panic, the ensuing volatility tends to be higher. Moreover, $\lambda _{1}$ and $\lambda _{2}$ are the transition rates of going down and going up, respectively. For example, $\lambda _{1}=24$ means the bull market will switch to bear market after it runs for about half a month, when time is measured in years.

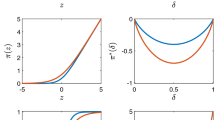
The values (fair prices) of the option for $p\in \{1,2\}$ on the interval $x\in [0,10]$ are plotted in Fig. 1. According to the numerical results, if in a bull market (i.e., $\alpha ^p(t)=1$), the option will be exercised by the buyer when the stock price goes below 4.20 or above 7.80. It is never optimal for the seller to cancel the option in a bull market. If in a bear market (i.e., $\alpha ^p(t)=2$), then things are different: the option will be exercised by the buyer when the stock price is smaller than 3.45. On the other hand, the seller cancels the option when the stock price goes above 8.05.

Fig. 1

Fair prices of game put option

Fig. 2

Fair price with no regime switching: Case 1

Fig. 3

Fair price with no regime switching: Case 2

Also, we note the following.

• (i) When the stock price is low enough, the option will always be exercised by the buyer to nail down profit regardless of market regimes (bull or bear). Naturally, the stock price level triggering exercise in a bear market is smaller than that in a bull market. That is, the buyer should stop somewhat earlier in a bull market due to the potential going up of the stock price. While in a bear market, there is still some room for the stock price to fall further and hence, the buyer can wait longer. As for the seller, the high penalty when the stock price is low prevents her from cancelling the option.

• (ii) When the stock is at a high price, the option will be terminated by the buyer in a bull market to beat the potential rise of the stock price and by the seller in a bear market to cut loss short owing to the down-trend of the market. We see that in this case the penalty is much less than that when the stock is at a low price, so that it could be put up with and actually gives the seller an opportunity to terminate the option. Even so, the stock price at which the seller to cancel is higher than that at which the buyer to exercise.

• (iii) In addition, the value (fair price) of the put option in a bear market is higher than that in a bull market. In fact, since both the buyer and the seller are not clairvoyant, the market trend observed at the time when they negotiate on the fair price of the option can strongly affect their judgements (though the stock price will fluctuate steadily seen from long-term). As a result, the fair price tends to be higher if the stock is going down.

Remark 4

In Guo and Zhang (2004), a “modified smooth fit” technique is used and a closed-form solution is obtained for American put options when the underlying Markov chain has only two states. In this example, we consider the American game options under the viscosity solution framework, and then numerical method is proceeded to demonstrate the effectiveness of our results. Compared with Guo and Zhang (2004), the viscosity solution framework allows us to study the option pricing problems in a more general setting such as the Markov chain has more than two states, where a closed-form solution is difficult to obtain; see Guo and Zhang (2004, Remark 3.5).

Remark 5

Finally, let us compare our results with those for the cases when there are no regime switching (i.e., $b(1)=b(2)$, $\sigma ^{2}(1)=\sigma ^{2}(2)$). The variational inequalities (3) now reduces to

$$\begin{aligned} \begin{aligned} \min \bigg \{\max \bigg \{\rho v(x) -bx\frac{\partial }{\partial x}v(x) -\frac{1}{2}\sigma ^{2}x^{2} \frac{\partial ^{2}}{\partial x^{2}}v(x), v(x)-g(x)\bigg \}, v(x)-h(x)\bigg \}=0, \end{aligned} \end{aligned}$$

according to which we compute the fair price of the option as well as the optimal stopping rules for both agents. Based on the parameters given above, we consider two different cases:

Case 1: Let $b=-1$, $\sigma ^{2}=0.1$. Besides, $\rho$ and K remain 3 and 9, respectively. The value (fair price) of the option on the interval $x\in [0,10]$ is plotted in Fig. 2. In this case, the option will be exercised by the buyer when the stock price moves below 2.735 and cancelled by the seller when the stock price goes above 6.72, respectively. We see that although the expected return rate of the stock is always negative, the seller will only cancel the option when the stock price is high. Here, a trade-off should be balanced by the seller between the penalty and the negative expected return rate.

Case 2: Let $b=1$, $\sigma ^{2}=0.01$. Also, $\rho$ and K remain 3 and 9, respectively. The value (fair price) of the option on the interval $x\in [0,10]$ is plotted in Fig. 3. In this case, the expected return rate is always positive, as a result, the option will be exercised by the buyer immediately all the time to avoid more potential loss (noting that there is no penalty imposed on the buyer).

5 Concluding remarks

In this paper, we solve the Dynkin game problems for switching diffusions in an infinite horizon. The value of the game is proved to be the unique viscosity solution of associated variational inequalities. Optimal stopping rules for both players are given in terms of the corresponding stopping regions, which are characterized by the “obstacle parts” of the variational inequalities. As an application, we provide a numerical example of the pricing of game put options.

For further research along this line, it would be interesting to extend the results to incorporate more realistic scenarios including the case of market trends being not completely observable, and the case where some other factors are involved, e.g., capital gains taxes and fixed transaction costs.