On two dominances of fuzzy variables based on a parametrized fuzzy measure and application to portfolio selection with fuzzy return

Abstract

Yang and Iwamura (Appl Math Sci 46:2271–2288, 2008) introduced a new fuzzy measure as a convex linear combination of possibility and necessity measures. This measure generalizes the credibility measure and the real parameter associated to the possibility measure is considered as the decision making’s optimism level. In this paper, we introduce by means of that measure, two new dominances as binary relations on fuzzy variables. The first one generalizes the first order dominance based on credibility measure and introduced recently by Tassak et al. (J Oper Res Soc 68:1491–1502, 2017) and the second one, based on the investor’s optimism level, is more stronger than the other. Moreover, we study some properties of those dominances and characterize them on the particular family of trapezoidal fuzzy numbers. We implement the second dominance in a numerical example to illustrate the impact of the investor’s attitude through the set of best portfolios.

Appendices

Appendix

Proof of Proposition 2

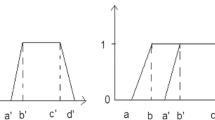
Let be $\lambda \in [0,1]$, $\xi _1=(a_1,b_1,c_1,d_1)$ and $\xi _2=(a_2,b_2,c_2,d_2)$ be two trapezoidal fuzzy variables whose respective distribution functions with respect to $M_{\lambda }$ are $\phi _{\lambda }^1$ and $\phi _{\lambda }^2$.

Let us assume that there exist $\alpha ,\beta \in [0,1]$ such that

$$\begin{aligned} \phi _{\alpha }^1(x)=\phi _{\beta }^2(x),\quad \forall x \in \mathbb {R} \end{aligned}$$

(9)

and let us prove that:

$$\begin{aligned} \phi ^1(x)=\phi ^2(x),\quad \forall x \in \mathbb {R}. \end{aligned}$$

• (1) First step

  Let us prove that $\left\{ \begin{array}{l} a_1=a_2,\\ b_1=b_2,\\ c_1=c_2,\\ d_1=d_2\\ \end{array} \right.$

  • (i) If $a_1\ne a_2$ (without loss of generality, we assume that $a_1 < a_2$).

    For x $\in ]a_1,a_2[$, according to (1) we have: $\phi _{\alpha }^1(x)\ne 0$ and $\phi _{\beta }^2(x)=0,$ that contradicts (9).

  • (ii) If $b_1\ne b_2$ (without loss of generality, we assume that $b_2 < b_1$).

    For $x_1,x_2\in ]b_2,b_1[$ such that $x_1\ne x_2$ and $x_1< c_1$, $x_2< c_2$, according to (1) we have: $\phi _{\alpha }^1(x_1)=0$ or $\phi _{\beta }^2(x_2)=0$ or $\phi _{\alpha }^1(x_1)= \phi _{\beta }^2(x_2)=\beta .$ The first two cases are obvious and we focus only on the third case: $\phi _{\alpha }^1(x_1)= \phi _{\beta }^2(x_2)=\beta \Longrightarrow \frac{\alpha (x_1-a_1)}{b_1-a_1}=\frac{\alpha (x_2-a_1)}{b_1-a_1}=\beta ,$ according to (1) and (9). We have: $(\frac{\alpha (x_1-a_1)}{b_1-a_1}=\frac{\alpha (x_2-a_1)}{b_1-a_1}=\beta ) \Rightarrow x_1=x_2$, which contradicts $x_1\ne x_2.$

  • (iii) If $c_1\ne c_2$ (without loss of generality, we assume that $c_2 < c_1$).

    For $x_1,x_2\in ]c_2,c_1[$ such that $x_1\ne x_2$ and $x_1> b_1$ , $x_2> b_2$, according to (1) we have: $\phi _{\alpha }^1(x_1)=1$ or $\phi _{\beta }^2(x_2)=1$ or $\phi _{\alpha }^1(x_1)= \phi _{\beta }^2(x_2)=\alpha .$ The first two cases are obvious and we focus only on the third case: $\phi _{\alpha }^1(x_1)= \phi _{\beta }^2(x_2)=\alpha \Longrightarrow \frac{\beta (d_2-x_1)+ x_1-c_2}{d_2-c_2}=\frac{\beta (d_2-x_2)+ x_2-c_2}{d_2-c_2}= \alpha$ according to (1) and (9). We have: ($\frac{\beta (d_2-x_1)+ x_1-c_2}{d_2-c_2}=\frac{\beta (d_2-x_2)+ x_2-c_2}{d_2-c_2}= \alpha ) \Longrightarrow x_1=x_2,$ that contradicts $x_1\ne x_2.$

  • (iv) If $d_1\ne d_2$ (without loss of generality, we assume that $d_1 < d_2$).

    For $x\in ]d_1,d_2[$, according to (1) we have: $\phi _{\alpha }^1(x_1)=1$ and $\phi _{\beta }^2(x)< 1,$ that contradicts (9).

    Finally, we have $a_1=a_2,b_1=b_2,c_1=c_2,d_1=d_2.$

• (2) Second step

  Let us prove that $\alpha =\beta$.

  According to the first step, we have $[b_2,c_2]=[b_1,c_1]$. Moreover, $x \in [b_1,c_1]\Longrightarrow \phi _{\alpha }^1(x_1)=\alpha$ and $x \in [b_2,c_2]\Longrightarrow \phi _{\beta }^2(x)=\beta$.

  Thus: ($x \in [b_1,c_1]\Longleftrightarrow x \in [b_2,c_2])$ and $\phi _{\alpha }^1(x_1) =\phi _{\beta }^2(x),$ that is, $\alpha =\beta$.

• (3) Third step

  Let us prove that $\phi ^1(x)=\phi ^2(x),\forall x \in \mathbb {R}.$

  By the fact that,

  $\phi _{\alpha }^1(x)=\phi _{\beta }^2(x),\forall x \in \mathbb {R}, \alpha =\beta$ and

  $$\begin{aligned} \left\{ \begin{array}{l} a_1=a_2,\\ b_1=b_2,\\ c_1=c_2,\\ d_1=d_2 \end{array} \right. \end{aligned}$$

  we can conclude according to (1) that: $\phi _{\alpha }^1(x_1)=\phi _{\lambda }^2(x),\forall x \in \mathbb {R},\forall \lambda \in [0,1]$, that means in the particular case where $\lambda =\frac{1}{2}$ (Liu 2004), $\phi ^1(x)=\phi ^2(x),\forall x \in \mathbb {R}.$ $\square$

Proof of Proposition 3

Proof of Theorem 1

Let be $\xi _1=(a_1,b_1,c_1,d_1)$ and $\xi _2=(a_2,b_2,c_2,d_)$ be two trapezoidal fuzzy variables with respective distribution functions $\phi _{\lambda _1}$ and $\phi _{\lambda _2}$ where $\lambda \in [0,1]$. $(\Rightarrow )$ We assume that $a_1< a_2$ or $a_1< b_2$ or $b_1< b_2$ or $c_1< c_2$ or $c_1< d_2$ or $d_1< d_2$ we prove that $\xi _1 \nsucceq _{d^{\lambda }_1} \xi _2,$ that is, there exists some $r_0\in \mathbb {R}$ such that $\phi _{\lambda _1}(x)(r_0)> \phi _{\lambda _2}(x)(r_0).$ We distinguish four cases:

• First case: $a_1< a_2$. Let consider $r\in ]a_1,a_2[;$ we have: $r> a_1\Rightarrow \phi _{\lambda _1}(r)> \phi _{\lambda _1}(a_1)=0$ and $r< a_2\Rightarrow \phi _{\lambda _2}(r)=0$, Thus $\phi _{\lambda _1}(r)>\phi _{\lambda _2}(r)$.

• Second case: $b_1< b_2$. Let consider $r\in ]b_1,b_2[,$ we have: $\phi _{\lambda _1}(r)>\phi _{\lambda _2}(r)$.

• Third case: $c_1< c_2$. Let consider $r\in ]c_1,c_2[,$ we have: $\phi _{\lambda _1}(r)>\phi _{\lambda _2}(r)$.

• Fourth case: $d_1< d_2$. Let consider $r\in ]d_1,d_2[,$ we have: $\phi _{\lambda _1}(r)>\phi _{\lambda _2}(r)$.

  Hence, we obtain: $\xi _1 \nsucceq _{d^{\lambda }_1} \xi _2$.

$(\Leftarrow )$ We assume that $a_1\ge a_2$,$b_1 \ge b_2$,$c_1\ge c_2$ and $d_1\ge d_2$ and we prove that $\xi _2$ is dominated by $\xi _1,$ that is, $\forall r \in \mathbb {R},\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

For that purpose, we have to study eight cases and conclude according to relation (1):

• First case: if $r\in ]-\infty , a_2]$, then: $\phi _{\lambda _2}(r)=\phi _{\lambda _1}(r)=0$ since $r\le a_2\le a_1$. Thus, $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

• Second case: if $r\in [a_2, a_1]$, then: $\phi _{\lambda _2}(r)=\frac{r-a_2}{2(b_2-a_2)}\ge 0$ and $\phi _{\lambda _1}(r)=0$. Thus, $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

• Third case: if $r \in [b_2, a_1]$ (with $a_1 \ge b_2$,) then we have: either $\phi _{\lambda _1}(r)=0$ and $\phi _{\lambda _2}(r)=\frac{1}{2}$ that is $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

In the same way, if $r\in [a_1, b_2]$ (with $a_1 < b_2$,) then we have: $\phi _{\lambda _1}(r)=\frac{r-a_1}{2(b_1-a_1)}$ and $\phi _{\lambda _2}(r)=\frac{r-a_2}{2(b_2-a_2)}$.

Let us prove that $\frac{r-a_1}{(b_1-a_1)}\le \frac{r-a_2}{2(b_2-a_2)}, \forall r\in [a_1, b_2]$.

Let us consider two functions f, g, respectively defined by: $f(r)=\frac{r-a_1}{(b_1-a_1)}$ and $g(r)=\frac{r-a_2}{(b_2-a_2)}$.

Let $r_0 \in ]a_1, b_2[$. $f(r_0)=g(r_0)\Leftrightarrow r_0=\frac{a_2(b_1-a_1)-a_1(b_2-a_2)}{(b_1-a_1)-(b_2-a_2)}$. $r_0-a_1=\frac{(b_1-a_1)(a_2-a_1)}{(b_1-a_1)-(b_2-a_2)}$ and $r_0-b_2=\frac{(b_2-b_1)(b_2-a_2)}{(b_1-a_1)-(b_2-a_2)}$ have the same sign because $a_1\ge a_2$ and $b_1\ge b_2$. This contradicts the fact that $r_0 \in ]a_1, b_2[$. On the other hand, $f(a_1)\le g(a_1)$, $f(b_2)\le g(b_2)$, f and g are strictly non-decreasing on $]a_1, b_2[$ and $f(r)\ne g(r), \forall r \in ]a_1, b_2[$, so $f(r)\le g(r), \forall r \in [a_1, b_2]$, that is $\frac{r-a_1}{(b_1-a_1)}\le \frac{r-a_2}{2(b_2-a_2)}$.

• Fourth case: if $r\in [\max (a_1,b_2), b_1]$, then we have: $\phi _{\lambda _2}(r)=\frac{1}{2}$ and $\phi _{\lambda _1}(r)=\frac{r-a_1}{2(b_1-a_1)}\le \frac{1}{2}$. Hence, $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

• Fifth case: if $r\in [b_1, c_2]$, then we have: $\phi _{\lambda _2}(r)=\phi _{\lambda _1}(r)=\frac{1}{2}$ since $b_2\le r\le b_1$ and $c_2\le r\le c_1.$ Hence, $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

• Sixth case: if $r\in [c_2,\min (c_1,d_2)]$, then we have: $\phi _{\lambda _2}(r)=1-\frac{r-d_2}{2(c_2-d_2)}\ge \frac{1}{2}$ and and $\phi _{\lambda _1}(r)=\frac{1}{2}$. Hence, $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

• Seventh case: if $r\in [\min (c_1,d_2), d_1]$, then by using a similar proof as presented in the third case, we get $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$.

• Eighth case: $\forall r\in [d_1, +\infty [, \phi _{\lambda _2}(r)=\phi _{\lambda _1}(r)=1.$ Hence, $\phi _{\lambda _1}(r)\le \phi _{\lambda _2}(r)$. $\square$