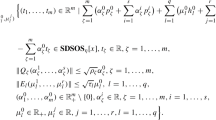Abstract
In this paper, we consider a convex quadratic multiobjective optimization problem, where both the objective and constraint functions involve data uncertainty. We employ a deterministic approach to examine robust optimality conditions and find robust (weak) Pareto solutions of the underlying uncertain multiobjective problem. We first present new necessary and sufficient conditions in terms of linear matrix inequalities for robust (weak) Pareto optimality of the multiobjective optimization problem. We then show that the obtained optimality conditions can be alternatively checked via other verifiable criteria including a robust Karush–Kuhn–Tucker condition. Moreover, we establish that a (scalar) relaxation problem of a robust weighted-sum optimization program of the multiobjective problem can be solved by using a semidefinite programming (SDP) problem. This provides us with a way to numerically calculate a robust (weak) Pareto solution of the uncertain multiobjective problem as an SDP problem that can be implemented using, e.g., MATLAB.
Similar content being viewed by others
References
Ben-Tal, A., Dick-Den, H., & Jean-Philippe, V. (2015). Deriving robust counterparts of nonlinear uncertain inequalities. Mathematical Programming, 149, 265–299.
Ben-Tal, A., El Ghaoui, L., & Nemirovski, A. (2009). Robust optimization. Princeton University Press.
Ben-Tal, A., & Nemirovski, A. (2001). Lectures on modern convex optimization: Analysis, algorithms, and engineering applications. SIAM.
Bertsimas, D., Brown, D. B., & Caramanis, C. (2011). Theory and applications of robust optimization. SIAM Review, 53(3), 464–501.
Blekherman, G., Parrilo, P. A., & Thomas, R. (2012). Semidefinite optimization and convex algebraic geometry. SIAM.
Boţ, R. I., Grad, S. M., & Wanka, G. (2009). Duality in vector optimization. Springer.
Burachik, R. S., & Jeyakumar, V. (2005). A dual condition for the convex subdifferential sum formula with applications. Journal of Convex Analysis, 12, 229–233.
Chinchuluun, A., & Pardalos, P. M. (2007). A survey of recent developments in multiobjective optimization. Annals of Operations Research, 154, 29–50.
Chuong, T. D. (2017). Robust alternative theorem for linear inequalities with applications to robust multi-objective optimization. Operations Research Letters, 45(6), 575–580.
Chuong, T. D. (2018). Linear matrix inequality conditions and duality for a class of robust multiobjective convex polynomial programs. SIAM Journal on Optimization, 28(3), 2466–2488.
Chuong, T. D. (2020). Robust optimality and duality in multiobjective optimization problems under data uncertainty. SIAM Journal on Optimization, 30(2), 1501–1526.
Chuong, T. D., & Jeyakumar, V. (2017). A generalized Farkas lemma with a numerical certificate and linear semi-infinite programs with SDP duals. Linear Algebra and its Applications, 515, 38–52.
Chuong, T. D., & Jeyakumar, V. (2021). Adjustable robust multi-objective linear optimization: Pareto optimal solutions via conic programming. (Submitted for publication).
Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197.
Doolittle, E. K., Kerivin, H. L. M., & Wiecek, M. M. (2018). Robust multiobjective optimization with application to Internet routing. Annals of Operations Research, 271, 487–525.
Ehrgott, M. (2005). Multicriteria optimization. Springer.
Ehrgott, M., Ide, J., & Schobel, A. (2014). Minmax robustness for multi-objective optimization problems. European Journal of Operational Research, 239(1), 7–31.
Eichfelder, G., Niebling, J., & Rocktaschel, S. (2020). An algorithmic approach to multiobjective optimization with decision uncertainty. Journal of Global Optimization, 77, 3–25.
Engau, A., & Sigler, D. (2020). Pareto solutions in multicriteria optimization under uncertainty. European Journal of Operational Research, 281, 357–368.
Georgiev, P. G., Luc, D. T., & Pardalos, P. M. (2013). Robust aspects of solutions in deterministic multiple objective linear programming. European Journal of Operational Research, 229, 29–36.
Goberna, M. A., Jeyakumar, V., Li, G., & Vicente-Perez, J. (2014). Robust solutions of multiobjective linear semi-infinite programs under constraint data uncertainty. SIAM Journal on Optimization, 24(3), 1402–1419.
Grant, M., & Boyd, S. (2014). CVX: Matlab software for disciplined convex programming, Version 2.1. http://cvxr.com/cvx
Hadka, D. (2014). MOEA framework user guide: A free and open source java framework for multiobjective optimization (Version 2.4). Retrieved May, 2018, from http://www.moeaframework.org/
Helton, J. W., & Nie, J. (2010). Semidefinite representation of convex sets. Mathematical Programming, 122(1), 121–64.
Ide, J., & Schobel, A. (2016). Robustness for uncertain multi-objective optimization: A survey and analysis of different concepts. OR Spectrum, 38(1), 235–271.
Jahn, J. (2004). Vector Optimization: Theory, applications, and extensions. Springer.
Jeyakumar, V. (2003). Characterizing set containments involving infinite convex constraints and reverse-convex constraints. SIAM Journal on Optimization, 13(4), 947–959.
Jeyakumar, V., & Li, G. (2010). Strong duality in robust convex programming: Complete characterizations. SIAM Journal on Optimization, 20, 3384–3407.
Kuroiwa, D., & Lee, G. M. (2012). On robust multiobjective optimization. Vietnam Journal of Mathematics, 40(2–3), 305–317.
Lee, J. H., & Jiao, L. (2021). Finding efficient solutions in robust multiple objective optimization with SOS-convex polynomial data. Annals of Operations Research, 296, 803–820.
Lee, J. H., & Lee, G. M. (2018). On optimality conditions and duality theorems for robust semi-infinite multiobjective optimization problems. Annals of Operations Research, 269(1–2), 419–438.
Luc, D. T. (1989). Theory of vector optimization. Lecture notes in economics and mathematical systems. Springer.
Miettinen, K. (1999). Nonlinear multiobjective optimization. Kluwer.
Nguyen, M.- T., & Cao, T. (2017). A hybrid decision making model for evaluating land combat vehicle system. In G. Syme, D. Hatton MacDonald, B. Fulton, & J. Piantadosi (Eds.), 22nd International congress on modelling and simulation (MODSIM2017), Hobart, Australia (pp. 1399–1405).
Nguyen, M.-T., & Cao, T. (2019). A multi-method approach to evaluate land combat vehicle system. International Journal of Applied Decision Sciences, 12(4), 337–360.
Nguyen, M.- T., Cao, T., & Chau, W. (2016). Bayesian network analysis tool for land combat vehicle systemevaluation. In 24th National conference of the Australian Society for Operations Research (ASOR), Canberra, Australia.
Niebling, J., & Eichfelder, G. (2019). A branch-and-bound-based algorithm for nonconvex multiobjective optimization. SIAM Journal on Optimization, 29(1), 794–821.
Peacock, J., Blumson, D., Mangalasinghe, J., Hepworth, A., Coutts, A., & Lo, E. (2019). Baselining the whole-of-force capability and capacity of the Australian Defence Force. In Proceedings of the MODSIM conference, Canberra, Australia.
Rahimi, M., & Soleimani-damaneh, M. (2018a). Isolated efficiency in nonsmooth semi-infinite multi-objective programming. Optimization, 67(11), 1923–1947.
Rahimi, M., & Soleimani-damaneh, M. (2018b). Robustness in deterministic vector optimization. Journal of Optimization Theory and Applications, 179(1), 137–162.
Ramana, M., & Goldman, A. J. (1995). Some geometric results in semidefinite programming. Journal of Global Optimization, 7, 33–50.
Rockafellar, R. T. (1970). Convex analysis. Princeton University Press.
Sion, M. (1958). On general minimax theorems. Pacific Journal of Mathematics, 8, 171–176.
Soyster, A. (1973). Convex programming with set-inclusive constraints and applications to inexact linear programming. Operations Research, 1, 1154–1157.
Steuer, R. E. (1986). Multiple criteria optimization: Theory, computation, and application. Wiley.
Vinzant, C. (2014). What is a spectrahedron? Notices of the American Mathematical Society, 61(5), 492–494.
Wiecek, M. M. (2007). Advances in cone-based preference modeling for decision making with multiple criteria. Decision Making in Manufacturing and Services, 1, 153–173.
Zalinescu, C. (2002). Convex analysis in general vector spaces. World Scientific.
Zamani, M., Soleimani-damaneh, M., & Kabgani, A. (2015). Robustness in nonsmooth nonlinear multi-objective programming. European Journal of Operational Research, 247, 370–378.
Zhou, A., Qu, B.-Y., Li, H., Zhao, S.-Z., Suganthan, P. N., & Zhang, Q. (2011). Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm and Evolutionary Computation, 1, 32–49.
Zhou-Kangas, Y., & Miettinen, K. (2019). Decision making in multiobjective optimization problems under uncertainty: Balancing between robustness and quality. OR Spectrum, 41, 391–413.
Acknowledgements
The authors are grateful to the associate editor and referees for their constructive comments and valuable suggestions which have contributed to the final version of the paper.
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by Defence Science Technology Group Strategic Research Investment project.
Appendix: Numerical examples
Appendix: Numerical examples
The following examples show how we can employ the SDP reformulation scheme obtained in Theorem 4.1 (Procedure 1) to find robust (weak) Pareto solutions of uncertain convex quadratic multiobjective optimization problems.
The first example is dealt with a family of uncertain convex quadratic multiobjective problems of (\(\hbox {EU}_c\)) by specifying the value c of the objectives, while the second example is concerned with a family of uncertain convex quadratic multiobjective problems of (EU\(_n\)) by specifying the dimension n of the decision variables.
Example 6.1
(Calculating Pareto solutions via SDP) Let us consider a family of uncertain convex quadratic multiobjective problems:

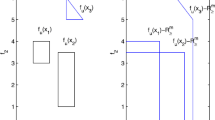
where \(c\in [0,+\infty )\) is a given parameter, \(u:=(u_1,u_2)\in \Omega \) and \(v:=(v_1,v_2)\in \Theta \) are uncertain parameters and \(f_r, r=1,2,3,4\) and \(g_l, l=1,2,3,4,5,6\) are bi-functions given by
Here, the uncertainty sets \(\Omega \) and \(\Theta \) are given by
Now, we consider the robust convex quadratic multiobjective problem of (\(\hbox {EU}_c\)) as follows:

Note that the problem (\(\hbox {ER}_c\)) can be expressed in terms of problem (RP), where \(\Omega _r:=\Omega , r=1,2,3,4,\) \( \Theta _l:=\Theta , l=1,2,3,4,5,6\) are described respectively by
and \(f_r, r=1,2,3,4, g_l, l=1,2,3,4,5,6\) are given respectively by \(Q^1:=I_2, Q^2:=Q^3:=\left( \begin{array}{cc} 0 &{} 0 \\ 0&{}1\\ \end{array} \right) , Q^4:=\left( \begin{array}{cc} 1 &{} 0 \\ 0&{}4\\ \end{array} \right) ,\) \( \xi ^1:=(-c,0), \xi ^2:=0_2, \xi ^3:=(0,2), \xi ^4:=(-c,1), \xi ^r_i:=0_2, r=1,2,3,4, i=1,2, \beta ^1:=\beta ^2:=1, \beta ^3:=\beta ^4:=0, \beta ^1_1:=\beta ^1_2:=\beta ^2_2:=\beta ^3_1:=1, \beta ^2_1:=\beta ^4_2:=-1, \beta ^3_2:=\beta ^4_1:=0\) and \( M^1:=\left( \begin{array}{cc} 0 &{} 0 \\ 0&{}1\\ \end{array} \right) ,\) \(M^2:=M^3:=M^5:=M^6:=0_{2\times 2}\), \(M^4:=I_2, \theta ^1:=\theta ^2:=(-1,0)\), \(\theta ^3:=(0,-1), \theta ^4:=0_2, \theta ^5:=(0,1)\), \(\theta ^6:=(1,0)\), \(\theta ^1_1:=(0,1), \theta ^1_2:=(1,0)\), \(\theta ^2_1:=\theta ^2_2\) \(:=\theta ^3_1:=\theta ^3_2:=\theta ^5_1:=\theta ^5_2\) \(:=\theta ^6_1:=\theta ^6_2:=0_2, \theta ^4_1:=(-1,0)\), \(\theta ^4_2=(0,-1), \gamma ^1:=-2c-4\), \(\gamma ^2:=\gamma ^3:=-3, \gamma ^4:=-c^2-2c-5\), \(\gamma ^5:=-4, \gamma ^6:=-c-4, \gamma ^1_1:=\gamma ^1_2\) \(:=\gamma ^2_2:=\gamma ^3_1\) \(:=\gamma ^4_1:=\gamma ^4_2:=\gamma ^5_1\) \(:=\gamma ^5_2:=\gamma ^6_1:=\gamma ^6_2:=0\), \(\gamma ^2_1:=1,\gamma ^3_2:=-1.\)
We now use the SDP reformulation, obtained in Theorem 4.1, to find a robust (weak) Pareto solution of problem (\(\hbox {EU}_c\)). Taking \(\tilde{x}:=(c,1),\) we see that \(g_l(\tilde{x},v) <0\) for all \(v\in \Theta \) and \(l=1,2,3,4,5,6.\) Thus, the characteristic cone \(K:={\text {coneco}} \{ (0_2,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v), v\in \Theta , l=1,2,3,4,5,6\}\) is closed by virtue of Remark 3.2. Moreover, by taking \(\tilde{u}:=\tilde{v}:=(0,0)\in \mathbb {R}^2,\) it holds that \(A^r+\sum \limits _{i=1}^2\tilde{u}_iA^r_i\succ 0, r=1,2,3,4\) and \(B^l+\sum \limits _{j=1}^2\tilde{v}_jB^l_j\succ 0, l=1,2,3,4,5,6\). Namely, all the assumptions of Theorem 4.1 are fulfilled in this setting.
Let \(\alpha :=(1,1,1,1)\in \mathrm{int}\mathbb {R}^4_+,\) and consider a corresponding robust weighted-sum optimization problem of (\(\hbox {ER}_c\)) as follows:

Note that the (scalar) weighted-sum problem (E\(_c\)) has optimal solutions as its objective function is a continuous function and its feasible set is a compact set.
The SDP reformulation problem of (E\(_c\)) is given by

Using the Matlab toolbox CVX (see e.g., Grant and Boyd, 2014), we solve the problem (E\(^{*}_c\)) with (for instance) \(c:=4\) and the solver returns the weighted-sum optimal value as \(-1.17157\) and an optimal solution of problem (E\(^{*}_c\)) with \(c:=4\) as \((\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,2,3,4, l=1,2,3,4,5,6)\), where \(\bar{w}=(2.0000, -2.9400\text {e-}08)\approx (2,0)\). By Theorem 4.1(iii), we conclude that \(\bar{w}=(2, 0)\) is a robust (weak) Pareto solution of problem (\(\hbox {EU}_c\)) with \(c:=4\). (In this setting, we can re-check directly that \(\bar{w}\) is a (weak) Pareto solution of problem (\(\hbox {ER}_c\)) with \(c:=4\).)
Similarly, we test with some other values of c (see Table 1). These the numerical tests are conducted on a computer with a 1.90GHz Intel(R) Core(TM) i7-8650U and 16.0GB RAM, equipped with MATLAB R2018b. In Table 1, “Robust Pareto Solutions” are optimal decision variables \(x:=(x_1,x_2)\) of (\(\hbox {EU}_c\)) and “Weighted-sum Values” are optimal values of (E\(^{*}_c\)) with the corresponding values of c.
Example 6.2
(Calculating Pareto solutions with higher dimensional decision variables) Let us consider a family of uncertain convex quadratic multiobjective problems:

where \(n\in \mathbb {N}, n\ge 3, \) is a given parameter, \(u:=(u_1,u_2)\in \Omega \) and \(v:=(v_1,v_2,v_3)\in \Theta \) are uncertain parameters and \(f_r, r=1,2,3,4,5\) and \(g_l, l=1,2,3\) are bi-functions given by
Here, the uncertainty sets \(\Omega \) and \(\Theta \) are given by
Now, we consider the robust convex quadratic multiobjective problem of (EU\(_n\)) as follows:

Note that the problem (ER\(_n\)) can be expressed in terms of problem (RP), where \(\Omega _r:=\Omega , r=1,2,3,4,5,\) \( \Theta _l:=\Theta , l=1,2,3\) are described respectively by
and \(f_r, r=1,2,3,4,5, g_l, l=1,2,3\) are given respectively by
\( Q^5:=0_{n\times n}, \xi ^1:=(0,0,\ldots ,0,-n), \xi ^2:=(-1,-1,\ldots ,-1), \xi ^3:=(0,2,0,\ldots ,0,-1), \xi ^4:=(-1,0,\ldots ,0,n), \xi ^5:=(1,1,\ldots ,1), \xi ^r_i:=0_n, r=1,2,3,4,5, i=1,2, \beta ^1:=\beta ^2:=1, \beta ^3:=\beta ^4:=\beta ^5:=0, \beta ^1_1:=\beta ^2_2:=\beta ^3_1:=\beta ^3_2:=\beta ^5_2:=1, \beta ^1_2:=\beta ^2_1:=\beta ^4_2:=\beta ^5_1:=-1, \beta ^4_1:=0\) and \( M^1:= Q_3, M^2:=I_{n}, M^3:=Q_1,\) \( \theta ^1:=(-1,0,\ldots ,0), \theta ^2:=0_n, \theta ^3:=(0,\ldots ,0,-1), \theta ^1_1:=(0,1,0,\ldots ,0), \theta ^1_2:=(1,0,\ldots ,0), \theta ^1_3:=0_n, \theta ^2_1:=\theta ^2_2:=\theta ^2_3:=0_n,\) \(\theta ^3_1:=(-1,0,\ldots ,0), \theta ^3_2=(0,-1,0,\ldots ,0), \theta ^3_3:=0_n, \gamma ^1:=-2n, \gamma ^2:=\gamma ^3:=-n, \gamma ^1_1:=\gamma ^1_2:=\gamma ^1_3:=\gamma ^2_2:=\gamma ^3_1:=\gamma ^3_2:=0,\) \(\gamma ^2_1:=\gamma ^3_3:=1,\gamma ^2_3:=-1.\)
We now use the SDP reformulation, obtained in Theorem 4.1, to find a robust (weak) Pareto solution of problem (EU\(_n\)). Taking \(\tilde{x}:=0_n,\) we see that \(g_l(\tilde{x},v) <0\) for all \(v\in \Theta \) and \(l=1,2,3.\) Thus, the characteristic cone \(K:={\text {coneco}} \{ (0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v), v\in \Theta , l=1,2,3\}\) is closed by virtue of Remark 3.2. Moreover, by taking \(\tilde{u}:=(\frac{1}{2},0)\in \mathbb {R}^2, \tilde{v}:=0_3\in \mathbb {R}^3,\) it holds that \(A^r+\sum \limits _{i=1}^2\tilde{u}_iA^r_i\succ 0, r=1,2,3,4,5\) and \(B^l+\sum \limits _{j=1}^3\tilde{v}_jB^l_j\succ 0, l=1,2,3\). Namely, all the assumptions of Theorem 4.1 are fulfilled in this setting.
Let \(\alpha :=(1,1,1,1,1)\in \mathrm{int}\mathbb {R}^5_+,\) and consider a corresponding robust weighted-sum optimization problem of (ER\(_n\)) as follows:

Note that the (scalar) weighted-sum problem (E\(_n\)) has optimal solutions as its objective function is a continuous function and its feasible set is a compact set.
The SDP reformulation problem of (E\(_n\)) is given by

Using the Matlab toolbox CVX (see e.g., Grant and Boyd, 2014), we solve the problem (E\(^{*}_n\)) with (for instance) \(n:=5\) and the solver returns the weighted-sum optimal value as \(+7.56512\) and an optimal solution of problem (E\(^{*}_n\)) with \(n:=5\) as \((\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,2,3,4,5, l=1,2,3)\), where \(\bar{w}=(0.2206, -0.1376, 0, 0, 1.8757)\). By Theorem 4.1(iii), we conclude that \(\bar{w}=(0.2206, -0.1376, 0, 0, 1.8757)\) is a robust (weak) Pareto solution of problem (EU\(_n\)) with \(n:=5\). (In this setting, we can re-check directly that \(\bar{w}\) is a (weak) Pareto solution of problem (ER\(_n\)) with \(n:=5\).)
Similarly, we test with some other values of n (see Table 2). These the numerical tests are conducted on a computer with a 1.90GHz Intel(R) Core(TM) i7-8650U and 16.0GB RAM, equipped with MATLAB R2018b. In Table 2, “Robust Pareto Solutions” are optimal decision variables \(x:=(x_1,\ldots , x_n)\) of (EU\(_n\)) and “Weighted-sum Values” are optimal values of (E\(^{*}_n\)) with the corresponding values of n.
Rights and permissions
About this article
Cite this article
Chuong, T.D., Mak-Hau, V.H., Yearwood, J. et al. Robust Pareto solutions for convex quadratic multiobjective optimization problems under data uncertainty. Ann Oper Res 319, 1533–1564 (2022). https://doi.org/10.1007/s10479-021-04461-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04461-x