Revenue and cost sharing contract in a dynamic closed-loop supply chain with uncertain parameters

Abstract

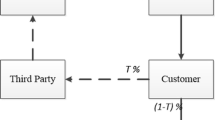
We model a closed-loop supply chain, made up of one manufacturer and one retailer, as a stochastic dynamic game. This paradigm allows us to simultaneously capture the strategic interactions between the agents, the intertemporal nature of the return of past-sold products for remanufacturing, and the uncertainty in the parameter values. We characterize and compare the solutions in two scenarios. In the no-sharing scenario, we assume that the manufacturer alone incurs the cost of the green activities aimed at incentivizing consumers to return previously purchased products at the end of their useful life. In the second scenario, namely, revenue and cost sharing contract, the retailer shares the cost of the green activities and the manufacturer transfers part of its revenues to the retailer. Numerical experiments are discussed.

Appendices

Appendix A

1.1 Proof of Lemma 1

Substituting $\frac{\theta _{i+1}}{\theta _{i}}=\eta$ in (2), we obtain

$$\begin{aligned} r\left( n_{l}^{t}\right)&=\theta _{1}\times f\left( G\left( n_{i_{t-1}}^{t-1}\right) \right) \times Q\left( n_{i_{t-1}}^{t-1}\right) +\theta _{1}\eta \times f\left( G\left( n_{i_{t-2}}^{t-2}\right) \right) \times Q\left( n_{i_{t-1}}^{t-2}\right) \nonumber \\&\quad +\theta _{1}\eta ^{2}\times f\left( G\left( n_{i_{t-3}}^{t-3}\right) \right) \times Q\left( n_{i_{t-2}}^{t-3}\right) +\cdots +\theta _{1}\eta ^{t-1}\times f\left( G\left( n^{0}\right) \right) \times Q\left( n^{0}\right) , \end{aligned}$$

(28)

Consider one-period lag

$$\begin{aligned} r\left( a\left( n_{l}^{t}\right) \right)&=\theta _{1}\times f\left( G\left( n_{i_{t-2}}^{t-2}\right) \right) \times Q\left( n_{i_{t-1}}^{t-2}\right) +\theta _{1}\eta \times f\left( G\left( n_{i_{t-3}}^{t-3}\right) \right) \times Q\left( n_{i_{t-2}}^{t-3}\right) \nonumber \\&\quad +\theta _{1}\eta ^{2}\times f\left( G\left( n_{i_{t-4}}^{t-4}\right) \right) \times Q\left( n_{i_{t-3}}^{t-4}\right) +\cdots +\theta _{1}\eta ^{t-2}\times f\left( G\left( n^{0}\right) \right) \times Q\left( n^{0}\right) , \end{aligned}$$

(29)

and multiply the above result by $\eta$, to get

$$\begin{aligned} \eta r\left( a\left( n_{l}^{t}\right) \right)&=\theta _{1}\eta \times f\left( G\left( n_{i_{t-2}}^{t-2}\right) \right) \times Q\left( n_{i_{t-1}}^{t-2}\right) +\theta _{1}\eta ^{2}\times f\left( G\left( n_{i_{t-3}}^{t-3}\right) \right) \times Q\left( n_{i_{t-2}}^{t-3}\right) \nonumber \\&\quad +\theta _{1}\eta ^{3}\times f\left( G\left( n_{i_{t-3}}^{t-3}\right) \right) \times Q\left( n_{i_{t-2}}^{t-3}\right) +\cdots +\theta _{1}\eta ^{t-1}\times f\left( G\left( n^{0}\right) \right) \times Q\left( n^{0}\right) . \end{aligned}$$

(30)

Compute the difference between (28) and (30) to obtain

$$\begin{aligned} r\left( n_{l}^{t}\right) -\eta r\left( a\left( n_{l}^{t}\right) \right) =\theta _{1}\times f\left( G\left( n_{i_{t-1}}^{t-1}\right) \right) \times Q\left( n_{i_{t-1}}^{t-1}\right) , \end{aligned}$$

or equivalently

$$\begin{aligned} r\left( n_{l}^{t}\right) =\eta r\left( a\left( n_{l}^{t}\right) \right) +\theta _{1}\times f\left( G\left( a\left( n_{l}^{t}\right) \right) \right) \times Q\left( a\left( n_{l}^{t}\right) \right) ,\quad r\left( n^{0}\right) =0. \end{aligned}$$

1.2 Proof of Lemma 2

Consider the total returns along the path from the root node $n^{0}$ to the terminal node $n^{T}\in \mathcal {N}^{T}$, that is, $\mathcal {P} (n^{T})=(n^{0},n^{1},\ldots ,n^{T})$, where $n^{t}\in S(a(n^{t-1}))$ for any $t=1,\ldots ,T$, which are given by

$$\begin{aligned} r(\mathcal {P}(n^{T}))=\sum _{\nu \in \mathcal {P}(n^{T})}r(\nu ), \end{aligned}$$

(31)

when $r(\cdot )$ satisfies the dynamics in (28) with initial condition $r(n^{0})=0$. Substituting r from (28) into (31) and grouping terms, we obtain

$$\begin{aligned} r(\mathcal {P}(n^{T}))&=Q(n^{0})f(G(n^{0}))\theta _{1}\left( 1+\eta +\ldots +\eta ^{T-1}\right) \nonumber \\&\quad +Q(n^{1})f(G(n^{1}))\theta _{1}\left( 1+\eta +\cdots +\eta ^{T-2}\right) \nonumber \\&\quad +\cdots +Q(n^{T-1})f(G(n^{T-1}))\theta _{1}. \end{aligned}$$

(32)

The coefficient of $Q(n^{0})$ can be interpreted as a share of sales at node $n^{0}$ that is totally returned along the path. It is natural to constrain this share to be no greater than one. As the upper bound of f $\left( \cdot \right)$ is $\upsilon _{1}$, we need to satisfy the inequality:

$$\begin{aligned} \theta _{1}\upsilon _{1}\left( 1+\eta +\cdots +\eta ^{T-1}\right) \le 1, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \theta _{1}\upsilon _{1}\le \frac{1-\eta }{1-\eta ^{T-1}}. \end{aligned}$$

If this condition is satisfied, the returns from sales in any further nodes on the path will be smaller than the sales because $1+\eta +\cdots +\eta ^{T-1}\ge 1+\eta +\cdots +\eta ^{t}$ for any $0<t<T-1$.

1.3 Proof of Proposition 1

The retailer’s optimization problem is given by

$$\begin{aligned} \max _{p(n_{l}^{t})\ge 0}{J}_{R}\left( p\right) =Q(n^{0})\Bigl (p(n^{0})-w \Bigr )+\sum _{t=1}^{T}\sum _{n_{l}^{t}\in {\mathcal {N}}^{t}}\pi \left( n_{l}^{t}\right) \delta ^{t}\Bigl \{Q(n_{l}^{t})\Bigl (p(n_{l}^{t})-w\Bigr ) \Bigr \}, \end{aligned}$$

which is independent of the manufacturer’s decision variable G and of the state variable r. Assuming an interior solution, the first-order optimality condition at node $n_{l}^{t}$ reads

$$\begin{aligned} \frac{d{J}_{R}}{dp(n_{l}^{t})}=\pi ^{n_{l}^{t}}\Bigl (\alpha ^{n_{l}^{t}}-2\beta ^{n_{l}^{t}}p(n_{l}^{t})+\beta ^{n_{l}^{t}}w\Bigr )=0, \end{aligned}$$

which yields

$$\begin{aligned} p(n_{l}^{t})=\frac{\alpha ^{n_{l}^{t}}+\beta ^{n_{l}^{t}}w}{2\beta ^{n_{l}^{t}}},\quad {n_{l}^{t}\in {\mathcal {N}}}^{t},t=0,\ldots ,T. \end{aligned}$$

(33)

Clearly, $p(n_{l}^{t})>0$ and, as ${J}_{R}\left( p\right)$ is concave in $p(n_{l}^{t})$, we have an interior maximum. We should mention that $p(n_{l}^{t})$ should be no less than w. Therefore, we need to satisfy condition

$$\begin{aligned} \frac{\alpha ^{n_{l}^{t}}}{\beta ^{n_{l}^{t}}}\ge w \end{aligned}$$

for any node ${n_{l}^{t}\in {\mathcal {N}}}^{t},t=0,\ldots ,T$.

Introduce the manufacturer’s pre-Hamiltonian

$$\begin{aligned}&\mathcal {H}_{M} (n_l^t,\lambda (S(n_l^t)),r(n_l^t),G(n_l^t))\\ {}&=\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) \left( w-c_{0}e^{-c_{r}r(n_{l}^{t})}\right) -\zeta G(n_{l}^{t}) \\&\quad +\delta \sum _{\nu \in S(n_l^t)}\frac{\pi ^{\nu }}{\pi ^{n_l^t}} \lambda (\nu )\delta \Big \{\eta r\left( n_{l}^{t}\right) +\theta _1 \left( \upsilon _1-(\upsilon _1-\upsilon _2)e^{-\kappa G(n_l^t)}\right) \left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) \Big \}, \end{aligned}$$

defined for any node $n_l^t\in {\mathcal {N}}^{t},t=0,\ldots ,T$, where $\lambda (S(n_l^t))$ is the vector of costate variables.

For any non-terminal node, we differentiate $\mathcal {H}_{M}$ with respect to $G(n_{l}^{t})$, and equating it to zero, we obtain

$$\begin{aligned} \frac{\partial \mathcal {H}_{M}}{\partial G(n_{l}^{t})}&=-\zeta +\delta \sum _{\nu \in S(n_{l}^{t})}\frac{\pi ^{\nu }}{\pi ^{n_{l}^{t}}}\lambda (\nu ) \Big \{\theta _{1}\kappa (\upsilon _{1}-\upsilon _{2})e^{-\kappa G(n_{l}^{t})}\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) \Big \}=0, \\ \Leftrightarrow G(n_{l}^{t})&=\kappa ^{-1}\ln \left[ \frac{\theta _{1}\kappa \delta (\upsilon _{1}-\upsilon _{2})}{2\zeta }\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}w\right) \left( \sum _{\nu \in S(n_{l}^{t})} \frac{\pi ^{\nu }}{\pi ^{n_{l}^{t}}}\lambda (\nu )\right) \right] ,\, n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}. \end{aligned}$$

We introduce the operator

$$\begin{aligned} \Phi (n_{l}^{t},\lambda )=\sum _{\nu \in S(n_{l}^{t})}\frac{\pi ^{\nu }}{\pi ^{n_{l}^{t}}}\lambda (\nu ), \end{aligned}$$

(34)

so the strategy $G(n_{l}^{t})$ can be rewritten in the following way:

$$\begin{aligned} G(n_{l}^{t})=\kappa ^{-1}\ln \left[ \frac{\theta _{1}\kappa \delta (\upsilon _{1}-\upsilon _{2})}{2\zeta }\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}w\right) \Phi (n_{l}^{t},\lambda )\right] ,\quad n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}. \end{aligned}$$

(35)

At the terminal node $n_{l}^{T}\in \mathcal {N}^{T}$, the manufacturer’s strategy does not influence the state variable r at any node of period T . As the payoff function of the manufacturer is linear and decreasing in G , then its equilibrium strategy equals zero for any terminal node:

$$\begin{aligned} G(n_{l}^{T})=0,\quad n_{l}^{t}\in \mathcal {N}^{T}. \end{aligned}$$

(36)

The costate variables are derived using the following system of equations:

$$\begin{aligned}&{\lambda }(n_{l}^{t})=\frac{\partial \mathcal {H}_{M}}{\partial r(n_{l}^{t}) }=\frac{c_{0}c_{r}}{2}e^{-c_{r}r(n_{l}^{t})}\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}w\right) +\delta \eta \Phi (n_{l}^{t},\lambda ), \nonumber \\&n_{l}^{t}\in {\mathcal {N}}{\setminus } \mathcal {N}^{T}, \nonumber \\&\lambda (n_{l}^{T})=\frac{\partial \mathcal {H}_{M}}{\partial r(n_{l}^{t})}= \frac{c_{0}c_{r}}{2}e^{-c_{r}r(n_{l}^{t})}\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}w\right) ,\quad n_{l}^{T}\in {\mathcal {N}}^{T}, \end{aligned}$$

(37)

where we substitute $p(n_{l}^{t})$ given by (33).

The transversality condition is $\lambda \left( \nu \right) =0$ for any node $\nu \in S(n^{t})$, meaning that returns after period T have no value to the manufacturer.

Substituting (37) in the expression of $G(n_{l}^{t})$ leads to the results in the Proposition.

1.4 Proof of Proposition 2

We first determine the manufacturer’s optimal control problem to the retailer announcing a retail price $p(n_{l}^{t})$ and a support rate $B(n_{l}^{t})$ for any $n_{l}^{t}\in \mathcal {N}^{t}$, $t=1,\ldots ,T$. The manufacturer aims to maximize

$$\begin{aligned} J_{M}(G,p,B,r)=\sum _{t=0}^{T}\sum _{n_{l}^{t}\in \mathcal {N}^{t}}\pi ^{n_{l}^{t}}\delta ^{t}\Bigl (\bigl (w-c(r(n_{l}^{t}))-I(r(n_{l}^{t}))\bigr ) Q(n_{l}^{t})-(1-B(n_{l}^{t}))d(G(n_{l}^{t}))\Bigr ) \end{aligned}$$

with $G(n_{l}^{t})\ge 0$ with respect to returns dynamics

$$\begin{aligned} r(n_{l}^{t+1})=\eta r(n_{l}^{t})+\theta _{1}(\upsilon _{1}-(\upsilon _{1}-\upsilon _{2})e^{-\kappa G(n_{l}^{t})})(\alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})),\,\,r(n^{0})=r_{0}\text { given}. \end{aligned}$$

(38)

The manufacturer’s Hamiltonian function for any node $n_{l}^{t}\in \mathcal {N }{\setminus } \mathcal {N}^{T}$ is as follows:

$$\begin{aligned}&\mathcal {H}_{M}(n_{l}^{t},\lambda _{M}(S(n_{l}^{t})),r(n_{l}^{t}),G(n_{l}^{t}),p(n_{l}^{t}),B(n_{l}^{t}))\\ {}&=(1- \phi )\left( w-c_{0}e^{-c_{r}r(n_{l}^{t})}\right) \left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) \\&\quad -\zeta \left( 1-B(n_{l}^{t})\right) G(n_{l}^{t})+\delta \Phi (n_{l}^{t},\lambda _{M})\\ {}&\quad \left[ \eta r(n_{l}^{t})+\theta _{1}(\upsilon _{1}-(\upsilon _{1}-\upsilon _{2})e^{-\kappa G(n_{l}^{t})})\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) \right] , \end{aligned}$$

where $\lambda _{M}\left( \cdot \right)$ is the costate variable appended by the manufacturer to the state dynamics in (38), and operator $\Phi$ is defined by (34). For any $n_{T}\in \mathcal {N}^{T}$ function $\mathcal {H}_{M}$ is defined as:

$$\begin{aligned} \mathcal {H}_{M}(n_{l}^{T},r(n_{l}^{T}),G(n_{l}^{T}),B(n_{l}^{T}))&=(1-\phi )\left( w-c_{0}e^{-c_{r}r(n_{l}^{T})}\right) \left( \alpha ^{n_{l}^{T}}-\beta ^{n_{l}^{T}}p(n_{l}^{Tt})\right) \\&\quad -\zeta \left( 1-B(n_{l}^{T})\right) G(n_{l}^{T}). \end{aligned}$$

Maximizing $\mathcal {H}_{M}$ with respect to $G(n_{l}^{t})$, we obtain

$$\begin{aligned} \frac{\partial \mathcal {H}_{M}}{\partial G(n_{l}^{t})}=-\zeta \left( 1-B(n_{l}^{t})\right) +\theta _{1}\kappa \delta (\upsilon _{1}-\upsilon _{2})e^{-\kappa G(n_{l}^{t})}\Phi (n_{l}^{t},\lambda _{M})\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) =0,\nonumber \\ \end{aligned}$$

(39)

and for the terminal nodes $n_{l}^{T}\in \mathcal {N}^{T}$ we have

$$\begin{aligned} G(n_{l}^{T})=0, \end{aligned}$$

(40)

because function $\mathcal {H} _{M}(n_{l}^{T},r(n_{l}^{T}),G(n_{l}^{T}),B(n_{l}^{T}))$ is a linear decreasing function of $G(n_{l}^{T})$.

Notice that under the assumptions of an interior solution and positive demand, $\Phi (n_{l}^{t},\lambda _{M})$ must satisfy the condition

$$\begin{aligned} \Phi (n_{l}^{t},\lambda _{M})Q(n_{l}^{t})\ge \frac{\zeta \left( 1-B(n_{l}^{t})\right) }{\theta _{1}\kappa \delta (\upsilon _{1}-\upsilon _{2})} \end{aligned}$$

to have a nonnegative $G(n_{l}^{t})$. The expression in the left-hand side of the inequality is the expected demand on the stage that follows the current node $n_{l}^{t}$.

The conditions on $\lambda _M (n_{l}^{t})$ are given by

$$\begin{aligned} \lambda _M (n_{l}^{t})= & {} \frac{\partial \mathcal {H}_{M}}{\partial r(n_{l}^{t})}=F^{n_l^t}=(1-\phi )c_0c_r e^{-c_r r(n_l^t)}\left( \alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})\right) +\delta \eta \Phi (n_l^t,\lambda _M),\nonumber \\ \end{aligned}$$

(41)

$$\begin{aligned}{} & {} n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^T, \nonumber \\ \lambda _M (n_{l}^{T})= & {} \frac{\partial \mathcal {H}_{M}}{\partial r(n_{l}^{T})}=F^{n_l^T}=(1-\phi )c_0c_r e^{-c_r r(n_l^T)}\left( \alpha ^{n_{l}^{T}}-\beta ^{n_{l}^{T}}p(n_{l}^{T})\right) , n_{l}^{T}\in \mathcal {\ N} ^T.\nonumber \\ \end{aligned}$$

(42)

This costate variable will play the role of an additional state variable in the retailer’s (leader’s) problem.

Following the proof of Theorem 7.1 in Basar and Olsder (1998, pp. 368–370), we obtain the Stackelberg strategy of the retailer. We have to maximize $J_{R}\left( G,p,B,r\right)$ in view of the unique optimal response of the follower (manufacturer). Therefore, the retailer is faced with the optimal control problem

$$\begin{aligned} \max _{\begin{array}{c} p(n_{l}^{t})>0 \\ 0\le B(n_{l}^{t})\le 1 \end{array}}J_{R}\left( G,p,B,r\right) =\sum _{t=0}^{T}\sum _{n_{l}^{t}\in \mathcal {N}^{t}}\pi ^{n_{l}^{t}}\delta ^{t}\Bigl (\bigl (p(n_{l}^{t})-w+I(r(n_{l}^{t}))\bigr ) Q(n_{l}^{t})-B(n_{l}^{t})d(G(n_{l}^{t}))\Bigr ), \end{aligned}$$

subject to state dynamics (38), relations on $\lambda _{M}$ dynamics given by (41) and (42), and equations (39) and (40).

The Hamiltonian of the optimal control problem of the retailer for any node $n_l^t\in \mathcal {N}{\setminus }\mathcal {N}^T$ is

$$\begin{aligned} H_R(n_l^t)&=\bigl (p(n_{l}^{t})-w+\phi (w-c_0e^{-c_rr(n_l^t)})\bigr ) Q(n_{l}^{t})-\zeta B(n_{l}^{t})G(n_{l}^{t}) \\&\quad +\delta \mu _r(n_l^t)\bigl ( \eta r(n_l^{t})+\theta _1(\upsilon _1-(\upsilon _1-\upsilon _2)e^{-\kappa G(n_l^t)})Q(n_{l}^{t})\bigr ) \\&+\delta \mu _{\lambda }(n_l^t) \bigl ((1-\phi )c_0c_r e^{-c_r r(n_l^t)}Q(n_{l}^{t})+\delta \eta \Phi (n_l^t,\lambda _M) \bigr ) \\&+\nu (n_l^t) \bigl (-\zeta \left( 1-B(n_{l}^{t})\right) +\theta _1\kappa \delta (\upsilon _1-\upsilon _2) e^{-\kappa G(n_l^t)}\Phi (n_l^t,\lambda _M)Q(n_{l}^{t})\bigr ), \end{aligned}$$

where $Q(n_{l}^{t})=\alpha ^{n_{l}^{t}}-\beta ^{n_{l}^{t}}p(n_{l}^{t})$. And for terminal nodes $n_l^T\in \mathcal {N}^T$ we have

$$\begin{aligned} H_R(n_l^T)&=\bigl (p(n_{l}^{T})-w+\phi (w-c_0e^{-c_rr(n_l^T)})\bigr ) Q(n_{l}^{T})-\zeta B(n_{l}^{T})G(n_{l}^{T}) \\&\quad +\mu _{\lambda }(n_l^T) (1-\phi )c_0c_r e^{-c_r r(n_l^T)}Q(n_{l}^{T}) \\&\quad -\nu (n_l^T)\zeta (1-B(n_{l}^{T})). \end{aligned}$$

Theorem 7.1 in Basar and Olsder (1998) (see pp. 368–370) gives the following system of relations:

$$\begin{aligned} \frac{\partial H_{R}(n_{l}^{t})}{\partial p(n_{l}^{t})}&=0,n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}, \end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial H_{R}(n_{l}^{T})}{\partial p(n_{l}^{T})}&=0,n_{l}^{T}\in \mathcal {N}^{T}, \end{aligned}$$

(44)

$$\begin{aligned} \frac{\partial H_{R}(n_{l}^{t})}{\partial B(n_{l}^{t})}&=0,n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}, \end{aligned}$$

(45)

$$\begin{aligned} \frac{\partial H_{R}(n_{l}^{T})}{\partial B(n_{l}^{T})}&=0,n_{l}^{T}\in \mathcal {N}^{T}, \end{aligned}$$

(46)

$$\begin{aligned} \frac{\partial H_{R}(n_{l}^{t})}{\partial G(n_{l}^{t})}&=0,n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}, \end{aligned}$$

(47)

$$\begin{aligned} \frac{\partial H_{R}(n_{l}^{T})}{\partial G(n_{l}^{T})}&=0,n_{l}^{T}\in \mathcal {N}^{T}, \end{aligned}$$

(48)

$$\begin{aligned} \mu _{r}(n_{l}^{t})&=\delta \sum _{\nu \in S(n_{l}^{t})}\frac{\pi ^{\nu }}{ \pi ^{n_{l}^{t}}}\frac{\partial H_{R}(\nu )}{\partial r(\nu )},n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}, \end{aligned}$$

(49)

$$\begin{aligned} \mu _{r}(n_{l}^{T})&=0,n_{l}^{T}\in \mathcal {N}^{T}, \end{aligned}$$

(50)

$$\begin{aligned} \mu _{\lambda }(n_{l}^{t+1})&=\frac{1}{\delta }\frac{\pi ^{a(n_{l}^{t+1})}}{ \pi ^{n_{l}^{t+1}}}\frac{\partial H_{R}(a(n_{l}^{t+1}))}{\partial \lambda _{M}(n_{l}^{t+1})},n_{l}^{t+1}\in \mathcal {N}{\setminus } n^{0}, \end{aligned}$$

(51)

$$\begin{aligned} \mu _{\lambda }(n^{0})&=0, \end{aligned}$$

(52)

$$\begin{aligned} \frac{\partial H_{M}(n_{l}^{t})}{\partial G(n_{l}^{t})}&=0,n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}, \end{aligned}$$

(53)

$$\begin{aligned} \frac{\partial H_{M}(n_{l}^{T})}{\partial G(n_{l}^{T})}&=0,n_{l}^{T}\in \mathcal {N}^{T}, \end{aligned}$$

(54)

$$\begin{aligned} \lambda _{M}(n_{l}^{t})&=F^{n_{l}^{t}},n_{l}^{t}\in \mathcal {N}{\setminus } \mathcal {N}^{T}, \end{aligned}$$

(55)

$$\begin{aligned} \lambda _{M}(n_{l}^{T})&=F^{n_{l}^{T}},n_{l}^{T}\in \mathcal {N}^{T}, \end{aligned}$$

(56)

with the state dynamics (38). Substituting the expressions of $H_{M}$, $H_{R}$, $F^{n_{l}^{t}},$ and $F^{n_{l}^{T}},$ we obtain the relations given in the theorem. In particular, (43) and (44) imply (14) and (15); (45) and (46) imply (18) and $\nu (n_{l}^{T})=0$ given in (19); (47) and (48) imply (16) and $B(n_{l}^{T})=0$ given in (19); (53) and (54) imply (17) and $G(n_{l}^{T})=0$ given in (19); (49) and (50) imply (23) and (24); (51) and (52) imply (25) and (26) ; (55) and (56) imply (21) and (22).

The solution of this system gives the Stackelberg equilibrium strategies G , B, and p and the equilibrium state trajectory r.

Appendix B

Table 8 presents the expected payoff for each player for different values of the sharing parameter, $\phi$.

Table 8 Expected payoff for each player for different sharing parameters

Tables 9, 10 and 11 show how changing parameters $\zeta$, $c_{0}$, $\eta$ affect the expected payoffs to the players. Comparing the numerical results in these tables with those in Table 8 provides more insight into the model. The changed parameters are bold italic in Tables 9, 10 and 11.

Table 9 Effect of $\zeta$ on the expected payoff for each player for different $\phi$

Table 10 Effect of $c_{0}$ on the expected payoff for each player for different $\phi$

Table 11 Effect of $\eta$ on the expected payoff for each player for different $\phi$

We can observe the following:

• 1. As expected, increasing $\zeta$ does not change the retailer’s expected payoff in the no-sharing scenario, while it reduces the manufacturer’s expected payoff. This change leads to slightly lower expected payoffs for both players in the RCSC scenario (see Table 9 in comparison with Table 8).

• 2. Increasing $c_{0}$ leads to a lower profit for the manufacturer in the no-sharing and RCSC scenarios. Although the retailer is not affected in the no-sharing scenario, it is highly penalized for a higher $c_{0}$ in the RCSC scenario (see Table 10 in comparison with Table 8).

• 3. The retailer is not affected by decreasing $\eta$ in the no-sharing scenario, but the manufacturer’s payoff decreases slightly. Decreasing $\eta$ leads to a negligible negative impact in both players’ expected payoffs in the RCSC scenario (see Table 11 in comparison with Table 8).

• 4. The manufacturer is much more sensitive to a higher $c_{0}$ than to a higher $\zeta$ and lower $\eta$. This may be due to the low level of green investments, which implies a low sensitivity to increasing $\zeta$.

• 5. In Tables 8, 9, 10, and 11 we show in bold font where RCSC is Pareto improving with respect to the no-sharing scenario.