Configurations in Coproducts of Priestley Spaces

Abstract

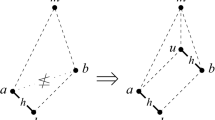
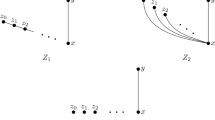
Let P be a configuration, i.e., a finite poset with top element. Let $\hbox{\textsf{Forb}}(P)$ be the class of bounded distributive lattices L whose Priestley space ℘(L) contains no copy of P. We show that the following are equivalent: $\hbox{\textsf{Forb}}(P)$ is first-order definable, i.e., there is a set of first-order sentences in the language of bounded lattice theory whose satisfaction characterizes membership in ${\hbox{\textsf{Forb}}}(P)$ ; P is coproductive, i.e., P embeds in a coproduct of Priestley spaces iff it embeds in one of the summands; P is a tree. In the restricted context of Heyting algebras, these conditions are also equivalent to $\hbox{\textsf{Forb}}_{H}(P)$ being a variety, or even a quasivariety.