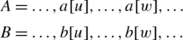Pattern matching with wildcards and gap-length constraints based on a centrality-degree graph

Abstract

Pattern matching with wildcards is a challenging topic in many domains, such as bioinformatics and information retrieval. This paper focuses on the problem with gap-length constraints and the one-off condition (The one-off condition means that each character can be used at most once in all occurrences of a pattern in the sequence). It is difficult to achieve the optimal solution. We propose a graph structure WON-Net (WON-Net is a graph structure. It stands for a network with the weighted centralization measure based on each node’s centrality-degree. Its details are given in Definition 4.1) to obtain all candidate matching solutions and then design the WOW (WOW stands for pattern matching with wildcards based on WON-Net) algorithm with the weighted centralization measure based on nodes’ centrality-degrees. We also propose an adjustment mechanism to balance the optimal solutions and the running time. We also define a new variant of WOW as WOW-δ. Theoretical analysis and experiments demonstrate that WOW and WOW-δ are more effective than their peers. Besides, the algorithms demonstrate an advantage on running time by parallel processing.

Appendix

1.1 A.1 Proof of Formula 5.2

Proof

$D_{node_{dep} \in S_{i,g}}$ is the number of paths from root nodes to leaf nodes through node _dep in S _i,g . It is equivalent to |S _i,g | (the number of occurrences in S _i,g ). Similarly, $D_{node_{dep} \in S_{j,g}} = |S_{j,g}|$.

According to Definition 5.1, $d_{\mathit{occ}_{k,i,g},S_{j,g}} =\allowbreak \sum_{node \in \mathit{occ}_{{k,i,g}}} D_{node \in S_{j,g}}$. Therefore, LWC[occ _h,i,g ] in Formula 5.2 holds.

Therefore, CWC[S _i,g ] in Formula 5.2 is confirmed. □

1.2 A.2 Proof of Theorems in Sect. 6.2

Theorem 6.1

If WON-Net(P,S) is null, WOW is complete. There exists $|O_{\mathit{PMG}}(P,S)|= |O_{\mathit{PMGO}}(P,S)|=|O_{\mathit{PMGO\_MAX}}(P,S)|=0$.

Proof

If WON-Net(P,S) is null, it means that there does not exist P in S. □

Property 6.1

$|O_{\mathit{PMGO\_Tg}}(P,S)|\leq \min\{ \min_{0 \le j < m}\{ C_{T_{g},j}\} ,\allowbreak \lfloor\frac{s_{T_{g},\max} - s_{T_{g},\min} + 1}{G_{N}} \rfloor\}$, where $O_{\mathit{PMGO\_Tg}}(P,S)$ is a subset of O _PMGO (P,S) on T _g , $C_{T_{g},j}$ is the number of nodes on the j-th layer in T _g , $s_{T_{g},\max}$ and $s_{T_{g},\min}$ are respectively the maximal and minimal node number in T _g , and G _N is the minimal global length of P.

Explanation

For each $T_{g}, |O_{\mathit{PMGO\_Tg}}(P,S)|$ is no more than $\min_{0 \le j < m}\{ C_{T_{g},j}\}$ based on the graph structure T _g , and no more than $\lfloor\frac{s_{T_{g},\max} - s_{T_{g},\min} + 1}{G_{N}} \rfloor$ with the global length constraint under the one-off condition. As in T ₁ and T ₂ in Example 3, $|O_{\mathit{PMGO\_T1}}(P,S)| =\min\{3, \lfloor\frac{20 - 12 + 1}{4} \rfloor\}=\{3,2\}=2$, and $|O_{\mathit{PMGO\_T2}}(P,S)| =\min\{1,\lfloor\frac{31 - 24 + 1}{4} \rfloor\}=\{1,2\}=1$.

Theorem 6.2

If

WOW is complete.

Proof

$|O_{\mathit{PMGO}}(P,S)| = \sum_{0 \le g < |\mathit{Net}|} |O_{\mathit{PMGO\_Tg}}(P,S)| \le\sum_{0 \le g < |\mathit{Net}|} \min\{ \min_{0 \le j < m}\{ C_{T_{g},j}\} , \lfloor\frac{s_{T_{g},\max} -s_{T_{g},\min} + 1}{G_{N}} \rfloor\}$. WOW is complete based on Property 6.1. □

Theorem 6.3

If P does not have duplicate sub-patterns (i.e. no p _i repeats (0≤i≤m−1)), WOW is complete.

Theorem 6.4

If each gap has the same upper and lower limits (∃N _i =M _j for ∀i, 0≤i<m−1), WOW is complete.

Proof

LMO/RMO in WOW is a transform of SAIL/RSAIL based on graph structure WON-Net(P,S) respectively. According to Theorems 2 and 4 in our previous work [16], we know that SAIL/RSAIL is complete while P does not have duplicate sub-patterns or each gap has the same upper and lower limits. Therefore, Theorems 6.3 and 6.4 are proved. □

Definition 6.1

If a node appears on different layers in WON-Net, the node is a free-node. In Fig. 1, there are six free-nodes: 4, 5, 6, 15, 16 and 17.

Theorem 6.5

If WON-Net(P,S) does not have free-nodes, WOW is complete.

Proof

There is the inverse negation of Theorem 6.5: “If WOW is incomplete, WON-Net(P,S) has free-nodes”.

Let $O_{\mathit{PMGO\_LMO}}(P,S)$ be the occurrence set by the LMO strategy in WOW, and $O_{\mathit{PMGO\_MAX}}(P,S)$ be the optimal one. Suppose $|O_{\mathit{PMGO\_LMO}}(P,S)|=1$ and $|O_{\mathit{PMGO\_MAX}}(P,S)|=2$. Let occurrences A=〈a[0],a[1],…,a[i],…,a[m−1]〉, $B=\langle b[0],b[1],\ldots,b[i],\ldots,\allowbreak b[m-1]\rangle \in O_{\mathit{PMGO\_MAX}}(P,S)$, and $\textit{Occ}=\langle \textit{occ}[0],\allowbreak \textit{occ}[1],\ldots, \textit{occ}[i],\ldots, \textit{occ}[m-1]\rangle \in O_{\mathit{PMGO\_LMO}}(P,S)$. Occ and A, Occ and B do not satisfy the one-off condition. There exist a[u]=occ[i] and b[w]=occ[k] (i≠k, 0≤u,w,i,k<m).

If u=w, there exists a[u]=b[w]. A and B do not satisfy the one-off condition. It is in contradiction with the assumption that A, $B\in O_{\mathit{PMGO\_MAX}}(P,S)$.

Let u<w. There are two possible cases as follows.

• 1. u≠i or w≠k

  If u≠i and a[u]=occ[i], the indexed position number a[u] is a free-node. It appears both on the u-th layer and the i-th layer in WON-Net(P,S). WON-Net(P,S) has free-nodes. It is proved while u≠i. Similarly, it can also be proved while w≠k.

• 2. u=i and w=k

  There is a[u]=occ[u]<b[u]<b[w]=occ[w]<a[w] according to the LMO strategy.

  

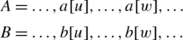
  There must exist a[t]<b[t] and b[t+1]<a[t+1], u≤t≤w−1.

  

Otherwise, there are two possible cases:

• a[t]≥b[t] and a[t+1]>b[t+1] (u≤t≤w−1). It is in contradiction with a[u]<b[u].

• a[t]<b[t] and a[t+1]≤b[t+1] (u≤t≤w−1). It is in contradiction with b[w]<a[w].

So, there exist a[t]<b[t] and b[t+1]<a[t+1] (u≤t≤w−1).

Thus there exists N _t ≤b[t+1]−b[t]<a[t+1]−b[t]<a[t+1]−a[t]≤M _t (u≤t≤w−1).

Under the gap-length constraints, 〈b ₀,b ₁,…,b _u ,…,b _t ,a _t+1,…,a _w ,…,a _m−1〉 is an occurrence of P in S. Thus, LMO will obtain another occurrence 〈b ₀,b ₁,…,b _u ,…,b _t ,a _t+1,…,a _w ,…,a _m−1〉. $O_{\mathit{PMGO\_LMO}}(P,S)= \{\textit{Occ},\langle b_{0},\allowbreak b_{1},\ldots, b_{u},\ldots, b_{t},a_{t+1},\ldots, a_{w},\ldots, a_{m-1}\rangle \}$. It is in contradiction with the assumption that $|O_{\mathit{PMGO\_LMO}}(P,S)|\allowbreak =1<\allowbreak |O_{\mathit{PMGO\_MAX}}(P,S)|=2$.

Therefore, the inverse negation that if WOW is incomplete, WON-Net(P,S) has free-nodes is true, and Theorem 6.5 is proved.

In addition, there also exists the completeness of O _PMG (P,S) based on WON-Net(P,S) as follows. □

Theorem 6.6

$|O_{\mathit{PMG}}(P,S)|=\sum_{0 \le g < |\mathit{Net}|} D_{T_{g}}$ and $D_{T_{g}} = D_{T_{g},0} =\cdots = D_{T_{g},j} =\cdots= D_{T_{g},m - 1}$, where $D_{T_{g},j} = \sum_{\{ node_{g,j}\}} D(\mathit{node}_{g,j}) |T_{g}$, and $D_{T_{g},j}$ is the sum of nodes’ centrality-degrees on the j-th layer in T _g .

Proof

O _PMG (P,S) is a set which contains all occurrences of P in S. O _PMG (P,S) can be divided into the sum of $O_{\mathit{PMG\_Tg}}(P,S)$ based on Property 4.1(2). $D_{T_{g},0}$ is the sum of the root nodes’ centrality-degrees in T _g . $D_{T_{g},0}$ is equivalent to $O_{\mathit{PMG\_Tg}}(P,S), 0\leq g<|\mathit{Net}|, 0\leq j<m$.

where $n^{k}_{g,j}$ is k-th node on the j-th layer in T _g , and $C_{T_{g},j}$ is the number of nodes on the j-th layer in T _g . □

1.3 A.3 The random data generator in Sect. 7.2

Artificial data are generated by the data generator to test the completeness of the pattern matching algorithms under the one-off condition. The data generator is described in [23]. The data generator is based on Algorithm DG (Algorithm 6) as follows. It can be proved with the complete solution of P in S under the one-off condition.

Algorithm 6

$\mathrm{DG}(L, \varSigma, P, N, M, \mathit{max\_sup})$

Given a character alphabet Σ, the gap-length constraints of pattern P, the length of the subject sequence S, and the maximal support max_sup, the data generator can produce S with the exact support value of P in S under the one-off condition. The support is equivalent to |OPMG(P,S)| and no more than max_sup.

The artificial data and the data generator program can be downloaded from the following website: http://dmic.hfut.edu.cn/HFUT_DMIC/DanGuo/test.