1 Introduction

In recent years, the use of new energy sources especially wind and solar is highly recommended [1]. These new energy sources are renewable, inexhaustible, environmentally friendly, and economical over a period of time [2, 3].

Among the renewable energy sources, solar energy is a suitable candidate as it allows direct conversion of this form of energy to the electrical energy by using photovoltaic (PV) systems [4]. Solar energy can be converted to the electrical energy by using a PV cell, albeit two limitations:

  • a) Extremely low conversion efficiency, especially under low irradiation [5] and

  • b) the dependency of power generation on the current atmospheric conditions (e.g., solar radiation and temperature), aging, and load conditions [6].

Therefore, it is ideal to maintain the PV operation at its maximum achievable efficiency at any time period. In other words, the optimum design of PV system is crucial for extracting maximum power from a PV cell. However, the nonlinear behavior of PV systems and the variations in the maximum power point (MPP) due to solar irradiance level and temperature complicate the tracking of MPP. It should be noted that the MPP can be achieved only at a specific operating point in the PV cells [7].

Several maximum power point tracking (MPPT) algorithms have been presented in the literature. These methods can be classified into three groups: model-dependent or offline, model-independent or online, and hybrid [4]. In the offline methods, the environmental conditions of a PV panel (such as radiation intensity and temperature) are usually used to generate the control signals. Some of the well-known offline methods are: open-circuit voltage method and tracking methods based on artificial intelligence-based algorithms. These methods can estimate MPP when quick changes occur under ambient conditions. In the online methods, instantaneous values of the PV output voltage or current are usually used to generate the control signals. Therefore, unlike in the offline methods, the control signal in the online methods is not constant, and its optimal value varies even in its steady state. Perturb and observe (P&O) method [8, 9] is one of the well-known online methods in this context.

The P&O method is widely used because of its low implementation-complexity and restricted numbers of measurement parameters. Although P&O is one of the successful MPPT methods; the operating point of a PV system fluctuates around the MPP. Therefore, the available energy is decreased. Furthermore, if the solar irradiance changes rapidly, the P&O technique fails to track the real points of maximum power [10].

In order to overcome the drawbacks of the P&O method, the incremental conductance (IncCond) method was proposed [11, 12]. The IncCond MPPT method is based on the fundamental comparison of instantaneous conductance to the incremental conductance. At the MPP, the values of conductance and incremental conductance are equal; however, with opposite signs. This method has medium implementation-complexity as compared to the P&O method. Use of the IncCond method involves a trade-off between the speed of convergence and the likelihood of oscillations around the MPP. The advantage of this algorithm includes provision of an effective solution when sudden changes under ambient conditions, while the main drawback includes the oscillations around the MPP [13, 14].

Examples of use of intelligent methods for this purpose include the work of Hiyama et al. [15], the pioneer groups that used multi-layer perceptron (MLP) neural network for the MPPT. In their method, the open-circuit voltage (V oc) was the only input of the artificial neural network that was obtained from the PV panels. The MLP output was a signal compared with the instantaneous voltage in order to generate the control signal needed to drive the PV panel to MPP through a proportional-integral controller. Syafaruddin et al. [16] used MLP to estimate the optimum voltage in a PV system, too. To achieve this goal, they used a fuzzy controller to contain the voltage of a DC/DC converter in partial-shading condition. Recently, Di Piazza et al. [17] followed an approach similar to the one proposed by Patcharaprakiti and Premrudeepreechacharn [10], but with the use of growing neural gas (GNG) network for the identification of PV cells and estimation of the solar radiation intensity. Finally, they used the estimated solar radiation to determine the MPP concluding that MLP neural network requires some more training data as compared to the GNG network.

In this paper, the concept of Di Piazza et al. [17] was modified to unique determination of the MPP. The GNG network is a self-organized map that cannot estimate the solar radiation intensity accurately, which is a continuous quantity. In other words, a network such as GNG cannot consistently estimate the solar radiation intensity and it causes loss in PV cells. In this study, a recurrent neural network (RNN) was used as it performs better in spatial and temporal information processing problems, including in real-time data prediction, dynamic system modeling and process control.

Two important tasks should be performed in designing a neural network: selection of an appropriate structure for the network and adjustment of the connection weights of the network. Determining the number of neurons in the hidden-layer of an RNN (as a structural parameter) has a considerable impact on its performance. Therefore, the number of hidden neurons in this study was determined by a discrete intelligent optimization algorithm (i.e., binary particle swarm optimization (BPSO) algorithm [18]).

In this study, the RNN weights were determined by two steps: a) by using the classic Levenberg-Marquardt (LM) algorithm that adjusts the weights and b) by using the gravitational search algorithm (GSA) to fine tune the weights of the RNN determined by the LM algorithm.

The optimized-RNN is used to estimate the solar radiation. The voltage of MPP is achieved by the estimated solar radiation; this voltage is provided to the control loop, as a reference voltage, in order to track the MPP.

The MPPT controller is an essential part of a PV system, as it drives the converter by changing the duty cycle of the DC/DC converter. In this manner, the converter forces the PV source to operate at its MPP. The design of an appropriate controller is also a challenging issue. A PV source has a strongly nonlinear output impedance and time-varying characteristics, therefore a simple conventional proportional-integral-derivative (PID) designed for a single operating point would not satisfy the control requirements of the boost converter and thus the fuzzy gain scheduling of PID (FGS-PID) method was used in this study as the MPPT control method.

The FGS-PID is composed of a two-stage controller [19]. At the first stage, a conventional PID controller is used whose main characteristics are the elimination of steady state error and the improvement of dynamic response. At the second stage, a fuzzy logic-based system [20, 21] is applied that supervises and modifies the operation (by gain scheduling) of the conventional PID controller [22, 23]. The fuzzy logic-based system updates the parameters of the conventional PID controller based on the error and error-difference in an online mode. For designing the rules of fuzzy logic-based system, training data of its inputs (i.e., error and error-difference) and its outputs (i.e., proportional gain, integral gain, and derivative gain) is needed which are ironically not available. To overcome this issue, the concept of Zhao et al. [22] on designing FGS-PID controller was adopted. They proposed a method for process control by using fuzzy rules while taking advantage of a fuzzy Sugeno system for gain scheduling of the conventional PID controller; however, the disadvantage of their method is that it includes several rules, some of which do not fire.

In order to enhance the efficiency of the FGS-PID method, Dounis et al. [19] used the input scale factor to convert the input values of the FGS. In this study, the rules of FGS were also optimized to increase the performance of the proposed MPPT method, which prevents the generation of high number of fuzzy rules and reduces the complexity of FGS. In order to optimize the fuzzy rules and to obtain a set of fuzzy rules, the subtractive clustering method was employed [24]. In this way, a first-order Sugeno fuzzy system was used for optimizing the FGS-PID module at the second stage of the proposed controller in this study.

The paper is organized as follows: Section 2 describes the details of PV cell and boost converter models. In Section 3, the details of the proposed system will be desc ribed. It deals with the two-stage controller and RNN-based MPPT as well as the optimization methods for these parts. In Section 4, the experimental results under four ambient conditions are reported. In addition, the performance of the proposed method was evaluated and compared to the recent researches in this field. Finally, Section 5 draws the conclusions of this study.

2 Photovoltaic system

The electrical model of a PV cell and its characteristics are introduced in this section. In addition, the employed boost converter model used in the simulations of this study is presented in this section.

2.1 PV cell model

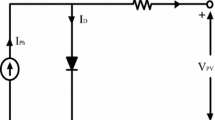
The electrical model of a PV cell has been proposed based on the Shockley diode (Fig. 1) [25]. Therefore, the electrical behavior of a PV cell can be simulated with regard to the changes in the ambient conditions such as temperature and solar radiation intensity. The solar radiation intensity and temperature are the input parameters in this PV cell model. The PV cell used in the simulations of this study is based on the Canadian Solar CS6X-300M - 300 Watt solar panel.

Fig. 1
figure 1

Electrical model of a PV cell

Full size image

In this way, (1) can be used to obtain I p v [26].

$$ I_{pv} =I_{ph} -I_{sat} \left( {e^{\frac{q({V_{pv} +I_{pv} R_{s}})}{nkT}}-1}\right) $$
(1)

where:

  • I p v and V p v represent the output current and output voltage of the PV cell, respectively

  • k is the Boltzmann constant (=1.38×10−23 J/K)

  • T is the module temperature [ ∘K]

  • n is the quality factor of the diode

  • I s a t is the saturation current of the PV cell

  • R s is the series resistance of the PV cell

Figure 2 depicts the nonlinear characteristics of the above-mentioned PV cell in different solar radiation intensity conditions [27]. The dynamic resistance (r d ) of PV cells was negative, while their static resistance was considered positive.

$$ r_{d} =\frac{\Delta V_{pv}} {\Delta I_{pv}} $$
(2)
Fig. 2
figure 2

Current-voltage characteristics of a PV cell under different solar radiation intensity conditions

Full size image

Figure 3a and b show the variation in the dynamic resistance of a PV cell under different temperature and solar radiation intensity conditions, respectively.

Fig. 3
figure 3

Dynamic resistance variations of a PV cell: a) in different temperature conditions and b) under different solar radiation intensity conditions

Full size image

2.2 Boost converter model

In this paper, the boost converter was used for MPPT. The state space model and the transfer function of boost converter are assumed similar to the converter proposed by Johansson [28].

As shown in Fig. 4, the output voltage of PV cell is V p v , its output current is I p v , its dynamic resistance is r p v , and the output voltage of the boost converter connected to the PV cell is V o . The duty cycle of control signal of the boost converter is called d, and according to a previous study [29], the second-order transfer function of the boost converter between the input voltage and the control signal can be written as (3) given below:

$$\begin{array}{@{}rcl@{}} \frac{V_{pv} (s)}{d(s)}&=&G(s)=\frac{K}{s^{2}+2\xi_{i} \omega_{i} s+\omega_{i}^{2}};\,K=\frac{V_{o}} {LC_{pv}} ,\, \omega_{i} \\ &=&\sqrt {\frac{-r_{pv} +R_{L}} {-r_{pv} LC_{pv}} } ,\, \xi_{i} =-\frac{-r_{pv} R_{L} C_{pv} +L}{2r_{pv} LC_{pv} \omega_{i}} \end{array} $$
(3)
Fig. 4
figure 4

Connection of a boost converter to a PV cell

Full size image

Since the dynamic resistance is used in the transfer function, the transfer function of the plant is time-variant and depends on the operating conditions. Therefore, a simple controller such as the conventional PID with constant and predetermined parameters is not sufficient to control the MPPT loop, and a controller with auto-tuned parameters is required.

3 Proposed system

In this paper, we proposed a method in which a FGS-PID module controls the PV system to drive its operation point to the MPP. The voltage of MPP is the set point of control loop; therefore, a recurrent neural model was used for inverse identification of the PV cell and estimation of the solar radiation intensity by which the set point of the control loop can be obtained. In fact, the duty of RNN is to search the MPP, while that of the FGS-PID controller is to apply this voltage to the PV system to enable the PV system operate in a point producing maximum power. The block diagram of the proposed system is shown in Fig. 5.

Fig. 5
figure 5

Block diagram of the proposed system

Full size image

3.1 FGS-PID controller

As stated in Section 2.1, since the dynamic resistance of a PV cell varies with changes in the voltage and the current of the operating point; the transfer function of boost converter is time-variant. Therefore, a conventional PID controller is not suitable for controlling the boost converter.

There are two methods for implementing a PID controller [22]. In the first method, the controller parameters are kept fixed during control after selection in an optimal manner [30]. For this purpose, the Ziegler-Nichols is the most well-known tuning method [31]. In the second method, the structure of the controller is similar to the first one but its parameters are adapted online based on the parameter estimation [32]. Such controllers are called adaptive PID controllers.

In this paper, a rule-based scheme was used for gain scheduling of PID controller in order to track the MPP and to control the boost converter [33]. The FGS method employs fuzzy rules and reasoning to determine the controller parameters, and the PID controller generates the control signal [34]. In fact, the fuzzy controller determines the parameters of a conventional PID controller based on the input information, including the error and error-difference. The conventional PID controller produces a suitable signal to control the boost converter. The block diagram of the control loop is shown in Fig. 6.

Fig. 6
figure 6

Block diagram of the control loop in the proposed system

Full size image

In order to generate the fuzzy rules, it is assumed that the ranges of K d and K p are as follows:

$$\begin{array}{@{}rcl@{}} &&K_{p} \in [{K_{p\min} ,K_{p\max}}] \\ &&K_{d} \in [{K_{d\min}, K_{d\max}}] \end{array} $$
(4)

Assuming the parameters K u and T u as the available parameters in the Ziegler-Nichols method [31], the appropriate ranges, based on experiments, are set as follows [19]:

$$ \begin{array}{ll} K_{p\, \min} =0.32K_{u} &\quad K_{p\, \max} =0.6K_{u} \, \\ K_{d\, \min} =0.08K_{u} T_{u} &\quad K_{d\, \max} =0.15K_{u} T_{u} \, \end{array} $$
(5)

In order to obtain K u and T u , the K d and K i parameters of the PID controller was set to zero in the closed-loop mode, then changed in the value of K p so that the output of system oscillates with a constant amplitude and frequency. In this mode, the amplitude of oscillating response determines K u and the period of oscillating signal determines T u [19].

When the appropriate ranges for proportional gain and derivative gain were determined, the proportional and the derivative gains can be normalized as in (6):

$$\begin{array}{@{}rcl@{}} &&{K}^{\prime}_{p} =\frac{K_{p} -K_{p\, \min} } {K_{p\, \max} -K_{p\, \min} } \\ &&{K}^{\prime}_{d} =\frac{K_{d} -K_{d\, \min} } {K_{d\, \max} -K_{d\, \min} } \end{array} $$
(6)

In the FGS-PID method, the PID parameters were determined based on error e(k) and error-difference Δe(k). The error is defined as the difference between the voltage of MPP (V MPP) and the real voltage of PV cell (V PV):

$$ e(k)=V_{MPP} -V_{PV} $$
(7)

In order to put e(k) and Δe(k) in [-1,1] range, (8) may be used:

$$ {e}^{\prime}(k)=\frac{e(k)}{| {\, V_{MPP} \, } |},{\Delta} {e}^{\prime}(k)={e}^{\prime}(k)-{e}^{\prime}(k-1) $$
(8)

The integral time-constant is determined based on the derivative time-constant as follows [19]:

$$ T_{i} =\alpha \times T_{d} $$
(9)

Finally, the integral gain can be obtained using (10):

$$ K_{i} =\frac{{K_{p}^{2}}} {\alpha \times K_{d}} $$
(10)

In order to obtain the PID parameters, the\({K}^{\prime }_{p} \), \({K}^{\prime }_{d} \), and α parameters were calculated by using the fuzzy rules based on e ′(k) and △e ′(k). Therefore, a fuzzy controller with 2 inputs and 3 outputs should be designed as shown in Fig. 7.

Fig. 7
figure 7

Inputs and outputs of the FGS system

Full size image

The sample fuzzy Mamdani rule for obtaining the parameters of \({K}^{\prime }_{p} \), \({K}^{\prime }_{d} \), and α are as follows:

$$\begin{array}{@{}rcl@{}} &&Rule\, i : If\,{e}^{\prime}(k)\, is\, A_{i} \, and\, {\Delta} {e}^{\prime}(k)\, is\, B_{i} \, then\, {K}^{\prime}_{p} \, is\, C_{i} ,\\ &&{K}^{\prime}_{d} \, is\,D_{i} ,\text{ and } \alpha \, is\, E_{i} \end{array} $$
(11)

where, i =1,2,...,m. In the above-mentioned fuzzy rule, A, B, C, D, and E are fuzzy sets on the corresponding supporting sets e ′(k), △e ′(k), \({K}^{\prime }_{p} \), \({K}^{\prime }_{d} \), and α, respectively. The membership function (MF) of these fuzzy sets for input variables e ′(k) and △e ′(k) are shown in Fig. 8. In this figure, N, P, and ZE represent negative, positive, and approximately zero, respectively. Similarly, S, M, and B represent small, medium, and big, respectively. Therefore, NM stands for negative-medium, PB for positive-big, etc.

Fig. 8
figure 8

MF for input variables \({e}^{\prime }(k)\) and \(\triangle {e}^{\prime }(k)\) [19]

Full size image

Figure 9, which includes 3 membership functions (small, medium, and big), depicts the MF for the output variables \({K}^{\prime }_{p} \) and\({K}^{\prime }_{d} \). The MF for output variable α is shown in Fig. 10, which includes 4 membership functions (small, medium-small, medium, and big).

Fig. 9
figure 9

MF for output variables \({K}^{\prime }_{p} \) and \({K}^{\prime }_{d}\) [19]

Full size image
Fig. 10
figure 10

MF for output variable α [19]

Full size image

In the present study, the fuzzy rules were adjusted according to the method proposed in a previous study [22], which is based on step-response of the system. Table 1 displays 49 rules related to the output\({K}^{\prime }_{p} \). Tables 2 and 3 show 49 rules related to the outputs \({K}^{\prime }_{d} \) and α, respectively.

Table 1 Fuzzy rules related to the output \({K}^{\prime }_{p}\) [19]
Full size table
Table 2 Fuzzy rules related to the output \({K}^{\prime }_{d}\) [19]
Full size table
Table 3 Fuzzy rules related to the output α [19]
Full size table

After the designing of the fuzzy system, the PID parameters were obtained based on the following equations:

$$ K_{p} ={K}^{\prime}_{p} ({K_{p\, \max} -K_{p\, \min} } )+K_{p\, \min} $$
(12)
$$ K_{d} ={K}^{\prime}_{d} ({K_{d\, \max} -K_{d\, \min} } )+K_{d\, \min} $$
(13)
$$ K_{i} =\frac{{K_{p}^{2}}} {\alpha \times K_{d}} $$
(14)

Figure 11 shows the value of error and error-difference (e and Δe) under ambient conditions with a solar radiation intensity of 1 sun and temperature of 25 ∘C. The step-response of the PV system for this situation is illustrated in Fig. 12.

Fig. 11
figure 11

Variations in error and error-difference in a solar radiation intensity of 1 sun and temperature of 25 ∘C

Full size image
Fig. 12
figure 12

Step response of the PV system in a solar radiation intensity of 1 sun and temperature of 25 ∘C

Full size image

The values of e and Δe in the FGS method were put in [-1,1] range; however, the variations of e and Δe did not cover the entire normalized range. With the use of trial and error and the study of e and Δe, the behavior under different ambient conditions and the operation range of e and Δe in the PV system were obtained as [ −0.4474, 1] and [ −0.5, 0.255], respectively.

To enhance the performance of the FGS method in this study, the subtractive clustering algorithm proposed by Chiu [35] was used for the optimization of the number of rules employed in the fuzzy system. In order to create the fuzzy rules by subtractive clustering algorithm, training data was needed based on the inputs and outputs of the system. The training data was obtained through Mamdani fuzzy system designed in this section. The training data was generated as follows: different values of e and Δe (as the system inputs) and the K p , K i , and K d parameters (as the system outputs) were considered for different ambient conditions. Therefore, a 600 ×5 matrix was prepared as the training data and categorized by subtractive clustering algorithm to finally obtain the fuzzy rules. Notably, the large number of rules may complicate the system, while the fewer numbers of rules can cause deficiency in the system operation. The parameters of subtractive clustering algorithm were selected as follows in this study for extracting the rules [24]:

$$ \begin{array}{ll} \text{radii} = 0.2 & \quad\text{quash factor} =1 \\ \text{accept ratio} = 0.1 & \quad\text{reject ratio} = 0.005 \end{array} $$
(15)

The membership functions of the input variables identified by subtractive clustering algorithm are shown in Fig. 13. The premise parameters identified by the cluster center (c) and standard deviation (σ) of the extracted Gaussian MF parameters are shown in Table 4. The fuzzy rules were created by implementing the subtractive clustering algorithm on the training data with the above-mentioned parameters. For the fuzzy system with the optimized rules, the first-order Sugeno fuzzy rules with 2 inputs and 3 outputs were used in the proposed model (16).

$$\begin{array}{@{}rcl@{}} &&{} Rule\, i\!:\!I\!\!f\, E\, i{\kern-.5pt}s\,{A_{1}^{i}} \, and\, {\Delta} E\, i{\kern-.5pt}s\, {A_{2}^{i}} \\ &&{\kern15pt} then\left\{\!\!\begin{array}{c} {K_{p} \,=\,P_{01}^{i} \,+\,P_{11}^{i} \!\times\! E\,+\,P_{21}^{i} \!\times\! {\Delta} E\, } \\ {K_{i} =\!P_{02}^{i} \,+\,P_{12}^{i} \!\times\! E\,+\,P_{22}^{i} \!\times\! {\Delta} E\,} \\ {K_{d} \,=\,P_{03}^{i} \,+\,P_{13}^{i} \!\times\! E\,+\,P_{23}^{i} \!\times\! {\Delta} E\, } \end{array}\right. i\,=\,1,...,M\\ \end{array} $$
(16)

The consequent parameters optimized on the basis of the least-squared error criterion are given in Table 5. The model output was computed by taking the weighted average of the output of the individual rules [36]. The parameters of three fuzzy rules are given in Table 5.

Fig. 13
figure 13

MF for the input variables optimized by subtractive clustering algorithm: a) error and b) error-difference

Full size image
Table 4 Parameters of the first-order Sugeno fuzzy input rules
Full size table
Table 5 Parameters of the first-order Sugeno fuzzy output rules
Full size table

3.2 Recurrent neural network

As mentioned earlier, a recurrent neural model was trained in this study to obtain the reference voltage corresponding to the MPP. RNN is an ANN with feedback connections with the capability to model dynamic systems. The Elman neural network [37] is an RNN model consisting of four layers: an input layer, a hidden layer, a context layer, and an output layer. The outputs of the context neurons were fed to the hidden neurons. The context neurons are known as memory units because they store the previous outputs of hidden neurons. In other words, the context layer in RNNs could cope with the historical data. Therefore, RNNs provide better solution than the conventional feed-forward networks. The Elman-type RNN structure used in this study is shown in Fig. 14. As seen in this figure, this network has 2 inputs: the voltage of PV cell and the current of PV cell at the operating point. The only output of the RNN is the solar radiation intensity.

Fig. 14
figure 14

Structure of the Elman-type RNN used in the present study

Full size image

The number of training data for the RNN was considered to be 600 samples. The number of neurons in the hidden-layer was m and the weights of the RNN were called w i j . The criterion for performance evaluation of the RNN is mean square-error (MSE). By using LM as the learning algorithm for the RNN, the performance (in terms of MSE on training data) is given in Table 6, where the number of hidden-layer neurons was assumed to be 1–10.

Table 6 MSE of Elman-type RNN when using different number of hidden-layer nodes
Full size table

As seen in Table 6, determination of the optimum number of neurons in the hidden-layer of RNN is important; this number was determined by the BPSO algorithm in this study. In addition, the hybrid method of classic LM algorithm and GSA heuristic algorithm [38] was used for the RNN training in this study. In order to train the RNN, the weights of the RNN were obtained, at first, by the LM training algorithm and then, the obtained weights by LM algorithm were used as the random initial population of GSA.

3.2.1 Determining optimum structure of RNN by BPSO

Particle swarm optimization (PSO) is an optimization technique inspired by the social behavior of birds [39]. In PSO algorithm, the system initially has a swarm of random solutions. Each potential solution (called a particle) is given a random initial velocity and then moved through the problem space. These particles reach the global best position by competition as well as cooperation among themselves.

The PSO algorithm shares common points with genetic algorithm; however, PSO does not have genetic operators such as crossover and mutation, and it has a different information sharing mechanism. The particles in PSO tend to converge to the best solution immediately, even in a local version. Therefore, the binary version of PSO was used in this study to determine the RNN topology (i.e., the number of hidden-layer neurons) instead of the traditional evolutionary computation methods [40].

In the PSO algorithm, D can be the dimension for the search space, the total number of particles may be rendered as s, the position of the i-th particle as X i , and the velocity of the i-th particle as V i . The best previous position (possessing the best fitness value) of the i-th particle is denoted as P i b , which is also called “pbest”. The index of the best “pbest” among all the particles is called “global best”, and the position P g is also called “gbest”. Therefore the particle updates its velocity and the positions according to the following equations:

$$\begin{array}{@{}rcl@{}} V_{i} (k+1)&=&wV_{i} (k)+c_{1} r_{1} (P_{i} (k)-X_{i} (k))\\ &&+c_{2} r_{2} (P_{g} (k)-X_{i} (k)) \end{array} $$
(17)
$$ X_{i} (k+1)=X_{i} (k)+V_{i} (k+1) $$
(18)

where, w is the inertia weight, c 1 and c 2 are the cognitive and social acceleration constants, and r 1 and r 2 are uniformly distributed random numbers in [0, 1] interval.

This algorithm is not influenced by the dimension or nonlinear form of the problem. This feature combined with the ease of implementation, lack of commitment to continuity of the cost function, and the ability to adapt to the dynamic environments makes this algorithm and its modifications suitable for using in different fields [41–46].

In the BPSO algorithm, the S-shaped transfer function is used as given in (19) [47].

$$ T(x)=\frac{1}{1+e^{-10x}} $$
(19)

In this study, the idea proposed by Wang et al. [18] was employed to determine the optimum number of the hidden-layer neurons of the RNN. A binary string with the length of “max_m” was used for RNN structure optimization and also after the implementation of the BPSO algorithm; the number of existing 1’s in this string offers the best number for the hidden-layer neurons of the RNN (Fig. 15).

Fig. 15
figure 15

Binary string structure for deciding the number of hidden-layer nodes in RNN

Full size image

The BPSO algorithm requires a cost function that is minimized by the algorithm. The cost function used in this study is given in (20):

$$ \text{Cost}=MSE+\beta \left( \frac{m}{\max\!\_m}\right) $$
(20)

In this equation, m indicates the number of neurons in the hidden-layer of Elman-type RNN, MSE is the performance criterion of the RNN after training, and β is a coefficient for keeping balance and limiting the excision of the hidden-layer neurons that should be selected appropriately. Therefore, when two particles demonstrate an identical MSE, the one with the least number of hidden nodes is preferable. In order to select the optimum number of hidden-layer neurons of the RNN, the parameters setting of BPSO algorithm was based on Table 7.

Table 7 BPSO parameters setting
Full size table

Figure 16 depicts the results of BPSO algorithm application to structure-optimization of the RNN. The best number of hidden-layer neurons and also the best and average responses are shown in this figure. As seen in this figure, the optimum number of hidden-layer nodes is 5, for which the fitness value is minimized for the best particle.

Fig. 16
figure 16

Finding the optimum number of hidden-layer neurons of RNN using BPSO algorithm: a) fitness value and b) the number of hidden nodes

Full size image

As shown in Fig. 16b, the optimum number of neurons is five as a trade-off between the structural complexity and the error performance. Although, if this trade-off is not considered, then the optimum number of hidden nodes should be set to 6 or 8, which resulted in a lower MSE (as reported in Table 6).

3.2.2 Optimizing weights of RNN with GSA

GSA, introduced by Rashedi et al. [38], is intended to solve optimization problems. This population-based heuristic algorithm is based on the law of gravity and mass interactions. It is comprised of a collection of search agents that interact with each other due to the gravitational force. The performance of objects is measured by their masses. Gravitational force causes a movement in which all objects under the force move towards other objects of comparatively heavier masses. The slow movement of heavier masses guarantees the exploitation step of the algorithm and corresponds to good solutions. GSA has the advantages of easy implementation, fast convergence, and low computational cost. Therefore, GSA was used in this study to fine-tune the connection weights of RNN. However, the PSO algorithm was also used in the performance comparisons. Notably, the direction of an agent in PSO algorithm was determined by using only two best positions, although the calculation of this direction was based on the overall force obtained by all other agents [38].

The masses actually obey the law of gravity (as shown in (21)) and the law of motion (as shown in (22)):

$$ F=\frac{GM_{1} M_{2}} {R^{2}} $$
(21)
$$ a=\frac{F}{M} $$
(22)

where, F represents the magnitude of the gravitational force, G is the gravitational constant, M 1 and M 2 are the mass of the first and second objects, and R is the distance between the two objects. In GSA, the agent has four parameters: position, inertial mass, active gravitational mass, and passive gravitational mass. The position of mass represents the solution of the problem. The gravitational and inertial masses are determined by using a fitness function. The algorithm is navigated by adjusting the gravitational and inertia masses, where each mass presents a solution. Object of a particular mass is attracted by the heaviest mass around it. Hence, the heaviest mass presents an optimum solution in the search space. This algorithm is also used in different applications to solve optimization problems [48].

Now, consider a system with N agents. The position of the i-th agent in the d-th dimension is expressed as X i . At time t, a force acts on mass j from mass i. This force is expressed as follows:

$$ F_{ij}^{d} =G(t)\frac{M_{pj} (t)\times M_{aj} (t)}{R_{ij} (t)+\varepsilon} \left( {x_{j}^{d}} (t)-{x_{i}^{d}} (t)\right) $$
(23)

where, M a j is the active gravitational mass related to agent j, M p i is the passive gravitational mass related to agent i, G(t) is the gravitational constant at time t, ε is a small constant, and R i j (t) is the Euclidian distance between two agents i and j:

$$ R_{ij} (t)=\| {X_{i} (t),X_{j} (t)} \|_{2} $$
(24)

The total force acting on mass i in the d-th dimension at time t is given as follows:

$$ {F_{i}^{d}} (t)=\sum\limits_{j\in Kbest,j\ne i}^{N} {rand_{j}} F_{ij}^{d} (t) $$
(25)

where, rand j is a random number in [0, 1] interval, Kbest is the set of first Kagents with the best fitness value and the biggest mass. In term of the Newton’s second law, the acceleration related to mass i at time t in the d-th dimension is given as follows:

$$ {a_{i}^{d}} (t)=\frac{{F_{i}^{d}} (t)}{M_{i i} (t)} $$
(26)

where, M i i is the inertial mass of the i-th mass. Therefore, the next velocity of an agent is considered as the fraction of its current velocity added to its acceleration. The position and velocity of the i-th mass are calculated as follows:

$$ {V_{i}^{d}} (t+1)=\left[ {rand_{i} \times {V_{i}^{d}} (t)} \right]+{a_{i}^{d}} (t) $$
(27)
$$ {x_{i}^{d}} (t+1)={x_{i}^{d}} (t)+{V_{i}^{d}} (t+1) $$
(28)

The gravitational constant takes an initial value at the beginning, which is reduced with time to control the search accuracy, as expressed below:

$$ G(t)=G_{0} e^{\left( {-\alpha \frac{t}{T}} \right)} $$
(29)

where, Tis the number of iterations and G 0 and αare predetermined constants. The gravitational mass and the inertial mass were updated by the following equations:

$$ m_{i} (t)=\frac{fit_{i} (t)-worst(t)}{best(t)-worst(t)} $$
(30)
$$ M_{i} (t)=\frac{m_{i} (t)}{\sum\limits_{j=1}^{N} {m_{j} (t)}} $$
(31)

where, fit i (t) represents the fitness value of the agent i at time t, and worst (t) and best (t) are defined as follows for a minimization problem:

$$ best(t)=\min_{j\in \{1,...,m\}} \,\, f\!i\!t_{j} (t) $$
(32)
$$ worst(t)=\max_{j\in \{1,...,m\}} \,\, f\!i\!t_{j} (t) $$
(33)

This algorithm also requires minimization of a cost function. The MSE criterion is selected as the cost function for optimizing the weights of the RNN. The GSA begins its operation with a random initial population. In this study, the obtained weights by the classic LM training algorithm was selected as the initial population of GSA to fine tune the weights of RNN.

The variables that should be selected optimally are the weights and biases of the RNN; therefore, for a network with 2 inputs, 5 hidden neurons, and 1 output neuron, the number of variables can be calculated at 46. The fitness values in different iterations when using GSA for weight optimization of the RNN (when GSA is used as a hybrid-party with the LM algorithm) are shown in Fig. 17. The prefix “best” in this figure refers to the best response and the prefix “mean” refers to the average of all responses.

Fig. 17
figure 17

Fitness values of GSA in different iterations during fine-tuning of the RNN weights

Full size image

The parameters setting of GSA, PSO algorithm, cuckoo optimization algorithm (COA) [49, 50], and grey wolf optimization (GWO) algorithm [51, 52] (as competitive algorithms for comparison purpose) in optimizing the weights of the RNN is given in Table 8.

Table 8 GSA, PSO, COA and GWO parameters setting for optimizing the RNN weights
Full size table

The parameter setting of COA and GWO algorithms was performed based on previous studies [50] and [52], respectively. The best fitness values in different iterations when using GSA, PSO, COA, and GWO algorithms for weight optimization of the RNN (when used as a hybrid-party with the LM algorithm) are shown in Fig. 18. As seen in this figure, the GSA demonstrates better performance both in the convergence speed and fitness values.

Fig. 18
figure 18

Performance comparison of GSA, PSO, COA, and GWO algorithms in fine-tuning of the RNN weights

Full size image

Figure 19 depicts the output of RNN in a three-dimension coordinate system in terms of the PV-cell voltage, the PV-cell current and the solar irradiance. As seen, the RNN properly estimated the solar radiation intensity for different values of voltage and current test data.

Fig. 19
figure 19

Estimation of solar radiation intensity by optimized-RNN over different test data

Full size image

4 Simulation and experimental results

This section deals with evaluation of the proposed system for the MPP tracking. For this purpose, the variation in the ambient conditions is considered and the performance of the system under different ambient conditions was studied. Therefore, concerning both speed and stability, four types of changes (abrupt, non-abrupt, and two general variations) were considered for evaluation of the system performance. The response of the proposed system was compared with three recent methods [17, 53, 54] and the P&O method.

4.1 Abrupt changes

It is believed that application of abrupt changes in ambient conditions (called Ambient Condition 1) may cause sudden variation in the radiation intensity and the temperature (step-wise) as mentioned in Table 9.

Table 9 Abrupt changes in the ambient conditions used in simulations
Full size table

Under these abrupt changes of ambient conditions, the response of the proposed system (based on Fig. 5 and in terms of V MPP) and the response of system based on P&O method are shown in Fig. 20 (in blue and green pens, respectively). In addition, tracking of the MPP voltage by FGS-PID controller of the proposed system (based on Fig. 6) and P&O method are marked in Fig. 20 with black and red pens, respectively. The proposed RNN-based system performed better than P&O method on application of abrupt changes to ambient conditions.

Fig. 20
figure 20

Response of the proposed system and the P&O method to the abrupt changes in ambient conditions

Full size image

For these abrupt changes in ambient conditions, the output power of the PV panel and the duty cycle of the control signal for driving the boost converter with the use of the proposed RNN-based system or by employing the P&O method are shown in Fig. 21.

Fig. 21
figure 21

Output power of the PV panel and the duty cycle of control signal with the use of the proposed system or P&O method-Ambient Condition 1

Full size image

The P&O method failed MPPT with respect to abrupt changes of ambient conditions, as occurred in [20 25] ms time interval (as the worst condition in Table 9).

4.2 Non-abrupt changes

The ambient changes mentioned in Section 4.1 were step-wise and possessed the ability to exhibit the performance of the proposed system in terms of the tracking speed. In order to evaluate the performance of the proposed system in terms of tracking accuracy, the non-abrupt changes in the ambient conditions were also considered (called Ambient Condition 2). In the simulations of this study, the non-abrupt changes in radiation intensity and temperature were considered as the patterns shown in Fig. 22.

Fig. 22
figure 22

Variations in solar radiation and temperature in the non-abrupt changes of ambient conditions

Full size image

Under these non-abrupt changes of ambient conditions, the response of the proposed system (based on Fig. 5 and in terms of V MPP) and the response of system based on the method proposed by Di Piazza et al. [17] are shown in Fig. 23 (marked in blue and green pens, respectively). Tracking of MPP voltage by FGS-PID controller of the proposed system (based on Fig. 6) and the system based on the method proposed by Di Piazza et al. [17] are shown in Fig. 23 (marked in black and red pens, respectively). The proposed RNN-based system performed better than the proposed system by Di Piazza et al. [17] when non-abrupt changes were applied to the ambient conditions.

Fig. 23
figure 23

Response of the proposed system and proposed method in a previous study [17] to the non-abrupt changes in ambient conditions

Full size image

For the mentioned non-abrupt changes in ambient conditions, the output power of the PV panel and the duty cycle of the control signal for driving the boost converter, with the use of the proposed RNN-based system or by employing the proposed system as in [17] are shown in Fig. 24. As shown in Fig. 24, the proposed RNN-based system performed better in MPPT than the proposed system in a previous study [17].

Fig. 24
figure 24

Output power of the PV panel and the duty cycle of control signal with the use of the proposed system or the proposed method in [17]-Ambient Condition 2

Full size image

4.3 General changes in ambient conditions

Under the abrupt ambient changes (mentioned in Section 4.1), the performance of the proposed system was exhibited in terms of the tracking speed. Under the non-abrupt ambient changes (mentioned in Section 4.2), the performance of the proposed system was exhibited in terms of the tracking accuracy. In order to evaluate the performance of the proposed system in terms of both the tracking speed and accuracy, the general changes in the ambient conditions should be considered. In our simulations, two types of general changes (called Ambient Condition 3 and Ambient Condition 4) were considered in the performance evaluation of the proposed system. The changes of the radiation intensity and temperature in these two ambient conditions are shown in Figs. 25 and 26, respectively.

Fig. 25
figure 25

Variations of solar radiation and temperature in Ambient Condition 3

Full size image
Fig. 26
figure 26

Variations of solar radiation and temperature in Ambient Condition 4

Full size image

The output power of the PV panel and the duty cycle of the control signal for driving the boost converter in these two ambient conditions with the use of the proposed RNN-based system are shown in Figs. 27 and 28, respectively.

Fig. 27
figure 27

Output power of the PV panel and the duty cycle of control signal with the use of the proposed system-Ambient Condition 3

Full size image
Fig. 28
figure 28

Output power of the PV panel and the duty cycle of control signal with the use of the proposed system-Ambient Condition 4

Full size image

4.4 Efficiency

In the previous subsections, the response of the proposed system was evaluated under four types of ambient conditions. The system efficiency in MPPT can be calculated by using (34). Based on this definition, the efficiency of the proposed system and two other methods (P&O and the proposed method in another study [17]) for four ambient conditions is reported in Table 10.

$$ \eta =\frac{{{\int}_{0}^{t}} {P(t)} dt}{{{\int}_{0}^{t}} {P_{\max} (t )} dt} $$
(34)

As depicted in Table 10, the proposed RNN-based system in this study showed the highest efficiency in all ambient conditions in comparison with the P&O method and the method proposed in another study [17] based on the GNG network. The reason of low-efficiency of the P&O method in abrupt changes of ambient conditions is that it cannot track the MPP in rapid changes of ambient conditions. The approach proposed by Di Piazza et al. [17] performs well, but as the GNG network is a self-organized map with discrete output space, its efficiency is lower than that of the proposed system, which employs an optimized-RNN with continuous output under different types of ambient conditions.

Table 10 Efficiency comparison of the proposed method with that of two other methods
Full size table

4.5 Performance comparison with competitive methods

In this subsection, the performance of the proposed MPPT method has been compared with that of four competitive methods: method proposed by Di Piazza et al. [17], optimized hybrid technique proposed by Murtaza et al. [53], hybrid method proposed by Moradi and Reisi [54], and the conventional P&O method. These algorithms were tested under diverse weather conditions and their performance was evaluated. Five cases of dynamic conditions based on Murtaza et al. [53] were considered for comparison of these algorithms. The ambient changes of these dynamic conditions are shown in Fig. 29.

Fig. 29
figure 29

Variations of solar radiation and temperature in five cases of dynamic conditions assumed in another study [53]

Full size image

The efficiency of the proposed method and the four above-mentioned methods are reported in Table 11. As seen in this table, the proposed MPPT method outperformed other techniques under the five mentioned cases of dynamic weather conditions.

Table 11 Efficiency comparison of the proposed method and four competitive methods based on five cases of dynamic conditions assumed in another study [53]
Full size table

5 Conclusion

Several methods have been proposed for tracking the MPP; but, due to the low efficiency of PV systems, improving the existing methods has become necessary. The system proposed in this paper for MPPT is composed of two main modules. The Elman-type RNN was one of these modules with the duty of finding the operating point at which the system produced the maximum power. The MPP was searched online by inverse identification of a PV cell by using the RNN and via estimation of the solar intensity. The other module was a controller, which had the duty of developing the operating point voltage closer to the MPP voltage. Considering nonlinear behavior of a PV cell, it is necessary to tune the controller online under changing environmental conditions. Therefore, this module was composed of a two-stage controller including a conventional PID and an FGS module for tuning the PID parameters (called FGS-PID).

The MPP voltage obtained by the RNN was applied to the control loop as a reference voltage; therefore, the operating point voltage of PV cell reached the voltage of maximum power by using the FGS-PID controller.

Speed and accuracy are important factors in the MPPT task. Therefore, in the proposed system, intelligent optimization techniques (such as BPSO and GSA) have been used to improve the mentioned factors of the MPPT. Optimizations of the structure of the RNN and the fuzzy rules were performed to increase the speed. Optimization of the weights of RNN has also been performed to further increase the accuracy. In addition, for selecting the optimum number of neurons in the hidden layer of RNN, a cost function was defined to provide a trade-off between speed and accuracy.

Simulation results demonstrated superior performance of GSA in comparison with that of particle swarm, cuckoo, and grey wolf optimization algorithms. The performance of the proposed MPPT method was evaluated under four different ambient conditions (abrupt, non-abrupt, and two general changes). Our experimental results showed that the proposed MPPT method is more efficient than the three competitive methods presented in recent years. As future research directions, other control strategies and neural models may be employed in the proposed framework. In addition, other optimization algorithms can also be used to fine-tune the structure and weights of the RNN such as the binary version of GSA [55] for RNN structure optimization and modified versions of GSA for fine tuning the weights. The hybrid optimization algorithms may also be used for joint optimization of structure and weights of RNN (as reported in [56] which is based on PSO and covariance matrix adaptation-evolution strategy).