Misinformation influence minimization by entity protection on multi-social networks

Abstract

Massive amounts of information are generated in various social media and spread across multi-social networks through individual forwarding and sharing, which greatly enhance the speed and scope of transmission, but also bring great challenges to the control and governance of misinformation. The characteristics of the spread of misinformation across multi-social networks are considered, this article investigates the novel problem of misinformation influence minimization by entity protection on multi-social networks, and systematically tackling this problem. We analyse the hardness and the approximation property of the problem. We construct a multi-social networks coupled method and devise a pruning and filtering rule. We develop a two-stage discrete gradient descent (TD-D) algorithm to solve NP-Hard problems. We also construct a two-stage greedy (TG) algorithm with the approximate guarantee to verify the algorithm we developed. Finally, the effectiveness of our proposed methods is analysed in synthetic and real multi-network datasets (contains up to 202K nodes and 2.5M edges). The results show that the ability of the TD-D and TG algorithms to suppress the spread of misinformation is basically the same, but the running time of the TG algorithm is much higher than (far more than 10 times) that of the TD-D algorithm.

Appendix A:: Proof

1.1 A. 1 Proof of theorem 1

Proof

The problem of MIE-m tries to minimize the number of entities ultimately activated by the misinformation,

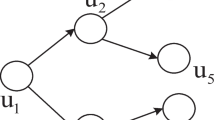
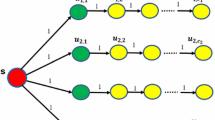
which is equivalent to maximizing the number of entities that are not influenced by $\mathfrak {R}$ such that $g({\varLambda })=\vert V \vert - \mathbb {E} \left [\sigma _{\mathfrak {R}}({\varLambda })\right ]$. We prove this by reducing the problem from the NP-complete set cover problem [50]. We set |V | = m. Let a ground set V = {v₁,v₂,⋯ ,v_m} and a collection of sets Λ = {Λ₁,Λ₂,⋯ ,Λ_y}, where $\cup _{j=1}^{y}{\varLambda }_{j} = V$. The set cover problem is to determine whether the union of K sets in Λ is equal to V. Next, we will show that the set cover problem can be regarded as a special case of the MIE-m problem. Given an arbitrary instance of the set cover problem, we construct a directed graph with m(n + 1) + y nodes. For each subset Λ_j we construct a related node a_j, for each element v_z (1 ≤ z ≤ m), construct n + 1 nodes $u_{z},{u_{z}^{1}},\cdots ,{u_{z}^{n}}$, and create a directed edge $(u_{z},{u_{z}^{i}})$ for each node ${u_{z}^{i}} (1\leq i\leq n)$ with probability $p_{u_{z}{u_{z}^{i}}}=1$. When element v_z belongs to Λ_j, we create a directed edge (a_j,u_z) with probability $p_{a_{j} u_{z}}=1$. Since the influence probability between nodes is 1, the dissemination of information is a fixed process. Therefore, the set covering problem is equivalent to deciding whether there are K nodes of Λ. □

1.2 A.2 Proof of theorem 2

Proof

When the number of online social networks is one, that is, n = 1, the account in an online social network can be equivalent to the entity. At this time, the problem of MIE-m is equivalent to the problem of misinformation influence minimization in single online social networks. We already know that the influence spread computation problem in online social network under the IC model is #P-hard [15]. Since the problem of misinformation influence minimization in online social networks is a special case of the problem of MIE-m, the influence spread computation problem in multi-social networks is also #P-hard, that is, computing $\sigma _{\mathfrak {R}}({\varLambda })$ is #P-hard in multi-social networks. □

1.3 A.3 Proof of proposition 2

Proof

We use the formula [51] to calculate the probability $\vartheta (w, \mathfrak {R})$ of w being activated by $\mathfrak {R}$ to prove it. In multi-social networks G(G¹,G²,⋯ ,Gⁿ), given $\mathfrak {R}$, we can get $\vartheta (w, \mathfrak {R})= 1-{\prod }_{i=1}^{n} {\prod }_{v^{i}\in N^{in}(w^{i})} [1-P^{fwd}(v^{i}) P^{inf}(v^{i},w^{i})]$ for any w ∈ V, where Nⁱⁿ(wⁱ) is the set of parent neighbours of entity w in online social network Gⁱ. Then, we obtain that $\vartheta (w, \mathfrak {R}) =1- {\prod }_{v\in N^{in}(w)} {\prod }_{i=1}^{n} [1-P^{fwd}(v^{i}) P^{inf}(v^{i},w^{i})] = 1- {\prod }_{v\in N^{in}(w)} 1-\hat {p}(v,w) = 1- {\prod }_{\hat {v}\in N^{in}(\hat {w})} 1-\hat {p}(\hat {v},\hat {w}) = \vartheta (\hat {w}, \mathfrak {\hat {R}})$ for any $\hat {w}\in \hat {V}$, where Nⁱⁿ(w) is the set of parent neighbors of entity w. Since $V=\hat {V}$, we have $\sigma _{\mathfrak {R}}({\varLambda })={\sum }_{w\in V} \vartheta _{{\varLambda }}(w, \mathfrak {R})={\sum }_{\hat {w}\in \hat {V}} \vartheta _{{\varLambda }}(\hat {w}, \mathfrak {R})=\sigma _{\mathfrak {\hat {R}}}(\hat {{\varLambda }})$ for all $\hat {{\varLambda }}\subseteq \hat {V}$, and the proposition follows. □

1.4 A.4 Proof of theorem 6

The proof framework is based on [52], but the supermodular function that makes the proof applicable to the problem of MIE-c requires some changes in the following. Given a coupled social network $G_{cou}(\hat {V}, \hat {E})$, an initial influence entities $\mathfrak {R}$ and a nonnegative nonincreasing supermodular function F(⋅) with supermodular curvature ϱ^F. We set $U = \hat {V} \backslash \mathfrak {R}$, then F(U) = 0. Let $W,M \subseteq U$, W = {w₁,w₂,⋯,w_a} and M = {m₁,m₂,⋯ ,m_b}, where W_i = {w₁,w₂,⋯ ,w_i} (i = 1,⋯ ,a) and M_s = {m₁,m₂,⋯ ,m_s} (s = 1,⋯ ,b) are sequences. For any $W\subseteq U$, we set b_w(W) = F(W∖w) − F(W).

Lemma 2

For any $W\subseteq U$, $F(W)={\sum }_{w_{j} \in U\backslash W} b_{w_{j}} (W_{a+j})$.

Proof

By the definition of b_⋅(⋅), we can get $F(W)= F(W_{a})= F(W_{a+1} )+ b_{w_{a+1}}(W_{a+1}) =b_{w_{a+1}}(W_{a+1})+ F(W_{a+2} ) + b_{w_{a+2}}(W_{a+2}) ={\cdots } = F(U) + {\sum }_{w_{j} \in U\backslash W} b_{w_{j}} (W_{a+j})$. Since F(U) = 0, the lemma is proved immediately. □

Lemma 3

For any $W,M \subseteq U$, it holds

$$ \begin{array}{@{}rcl@{}} \begin{aligned} F(W\cap M)&=F(M) + \sum\nolimits_{w_{j} \in M\backslash W} b_{w_{j}}(M\cap W_{a+j})\\ &=F(W)+\sum\nolimits_{m_{z} \in W\backslash M} b_{m_{z}} (W\cap M_{b+z}). \end{aligned} \end{array} $$

Proof

F(M ∩ W) = F(M ∩ W_a) = F((M ∩ W_a+ 1)∖w_a+ 1). If w_a+ 1 ∈ M∖W, we obtain F((M ∩ W_a+ 1)∖w_a+ 1 $)=F(M\cap W_{a+1} )+ b_{w_{a+1}}(M \cap W_{a+1} )$. For any w_a+ 1∉M, we have F({M ∩ W_a+ 1}∖w_a+ 1) = F(M ∩ W_a+ 1),⋯. Finally, we can deduce that $F(M\cap W)=F(\{ M \cap W_{a} \} \cup \{ M\backslash W \}) + {\sum }_{w_{j}\in M\backslash W} b_{w_{a+j}} (M \cap$ $W_{a+j})= {\sum }_{w_{j} \in M\backslash W} b_{w_{a+j}} (M\cap W_{a+j}) + F(M)$. Then the first equation proof is complete. Using a similar method, we can get $F(W\cap M)=F(W)+\sum \nolimits _{m_{z} \in W\backslash M} b_{m_{z}} (W\cap M_{b+z})$.

Given that Opt is an optimal solution to the problem of MIE-c, the TG algorithm consecutively acquires the sequences $C_{0} = \varnothing$, C₁ = {c₁}, ⋯, C_i = {c₁,c₂,⋯ ,c_i}, ⋯, C_K = {c₁,c₂,⋯ ,c_K}. Suppose r = |U|−|C_i|, $\overline {W} =U \backslash W$, $\overline {W}_{i} =U \backslash W_{i}$, and $w_{j} \in \overline {W}_{i}$. Without causing ambiguity, we abbreviate $b_{c_{i}}(C_{i})$ as b_i. Then, we can derive Theorem 7. □

Theorem 7

For i = 1, 2,⋯ ,K, it holds

$$ \begin{array}{@{}rcl@{}} F(Opt) \geq (r-s_{i}) b_{i} + \sum\limits_{j: c_{j} \in \overline{C_{i}} \cap \overline{Opt} } b_{j} - \eta \sum\limits_{j: c_{j} \in \overline{C_{i}} \backslash \overline{Opt}} b_{j} \end{array} $$

where $s_{i} = \vert \overline {Opt} \cap \overline {C_{i}} \vert$ and $\eta = \frac {{\varrho }^{F} }{1- {\varrho }^{F}}$.

Proof

Given any $W,\ M \subseteq U$, from Lemma 3, we have $F(M) = F(W)+ {\sum }_{m_{z} \in W \backslash M} b_{m_{z}} (W \cap M_{b+z})$ $-{\sum }_{w_{j} \in M \backslash W} b_{w_{j}}(M \cap W_{a+j})$. By the definition of supermodular and ϱ^F, we have $b_{w_{j}} (M \cap W_{a+j}) \leq b_{w_{j}}(w_{j}) \leq \frac {1}{1 - {\varrho }^{F}} b_{w_{j}}(U) \leq \frac {1}{1 - {\varrho }^{F}} b_{w_{j}}(W_{a+j})$. Since $b_{m_{z}} (W \cap M_{b+z}) \geq b_{m_{z}} (W)$ for all m_z ∈ W∖M. Then, we can obtain $F(M) \geq {\sum }_{w_{j} \in \overline {W} } b_{w_{j}} (W_{a+j}) +{\sum }_{m_{z} \in \overline {M} \backslash \overline {W}} b_{m_{z}} (W)- \frac {1}{1-{\varrho }^{F}} {\sum }_{w_{j} \in \overline {W} \backslash \overline {M}} b_{w_{j}}(W_{a+j})$ $={\sum }_{w_{j} \in \overline {W} \cap \overline {M} } b_{w_{j}} (W_{a+j}) +{\sum }_{m_{z} \in \overline {M} \backslash \overline {W}} b_{m_{z}} (W)- \frac {{\varrho }^{F} }{1- {\varrho }^{F}} {\sum }_{w_{j} \in \overline {W} \backslash \overline {M}} b_{w_{j}}(W_{a+j})$.

Let M = Opt, W = C_i and $\eta = \frac {{\varrho }^{F} }{1- {\varrho }^{F}}$, we can get $F(Opt) \geq {\sum }_{m_{z} \in \overline {Opt} \backslash \overline {C_{i}}} b_{m_{z}} (C_{i}) + {\sum }_{c_{j} \in \overline {C_{i}} \cap \overline {Opt} } b_{c_{j}} (C_{i+j})$ $-\eta {\sum }_{c_{j} \in \overline {C_{i}} \backslash \overline {Opt}} b_{c_{j}}(C_{i+j})$. By definition of Opt and C_i, for any $m_{z} \in \overline {Opt} \backslash \overline {C_{i}}$, $b_{m_{z}} (C_{i}) \geq b_{c_{i}} (C_{i})$. Therefore, ${\sum }_{m_{z} \in \overline {Opt} \backslash \overline {C_{i}}} b_{m_{z}} (C_{i}) \geq \vert \overline {Opt} \backslash \overline {C_{i}} \vert \cdot b_{c_{i}} (C_{i}) = \vert \overline {Opt} \backslash \{ \overline {Opt} \cap \overline {C_{i}} \} \vert \cdot b_{i} = (r-s_{i}) b_{i}$, where $s_{i} = \vert \overline {Opt} \cap \overline {C_{i}} \vert$. Finally, we get $F(Opt) \geq (r-s_{i}) b_{i} + {\sum }_{j: c_{j} \in \overline {C_{i}} \cap \overline {Opt} } b_{j} - \eta {\sum }_{j: c_{j} \in \overline {C_{i}} \backslash \overline {Opt}} b_{j}$. □

Given C = C_K, $\overline {C}=\{c_{1},\cdots ,c_{j},\cdots , c_{r}\}$ and $\overline {C_{j}} =\{c_{1},c_{2},\cdots ,c_{j} \}$. Let $\overline {Opt} \cap \overline {C} = \{ u_{1}, u_{2}, \cdots , u_{s}\}$, where s ≤ r, that is {u₁,u₂,⋯ ,u_s} be the elements not contained in Opt or C. Suppose $b_{j}= F(C\cup \{\overline {C_{j}}\backslash c_{j}\})-F(C\cup \overline {C_{j}})$. By Lemma 2, we can obtain $F(C)={\sum }_{j: c_{j} \in \overline {C} } b_{j}$. Then, the approximation ratio is defined as $\frac {F(C)}{F(Opt)} = {\sum }_{j: c_{j} \in \overline {C} } \frac {b_{j}}{F(Opt)}$. Define $y_{j} := \frac {b_{j}}{F(Opt)}, j \in [r]$. Since b_j ≥ 0, then y_i ≥ 0. We define $L(\overline {Opt} \cap \overline {C}) = {\sum }_{j: c_{j} \in \overline {C} } \frac {b_{j}}{F(Opt)}$.

Considering 1 ≤ s ≤ r, for the variables y_j, there are r constraints. Hence, the worst-case approximate ratio of $\frac {F(C)}{F(Opt)}$ can be expressed as the following Linear Programming (LP).

$$ \begin{array}{@{}rcl@{}} &L(\{ u_{1}, \cdots, u_{s}\}) =\max \sum\nolimits_{j=1}^{r} y_{j}\\ &s.t.\ \ y_{j} \geq 0,\ j=1,\cdots,r \end{array} $$

(A1)

$$ \begin{array}{@{}rcl@{}} \begin{bmatrix} r & & & & & & & & \\ -\eta & r & & & & & & & \\ {\vdots} &\vdots&{\ddots} & & & & & & \\ -\eta &-\eta &{\cdots} & r & & & & & \\ -\eta &-\eta &{\cdots} & 1 & r-1 & & \multicolumn{2}{l}{\raisebox{1.2ex}[0pt]{\Huge0}} & \\ {\vdots} &\vdots& &\vdots&\vdots&\ddots& & & \\ -\eta &-\eta &{\cdots} & 1 & 1 &\cdots&r-s & & \\ {\vdots} &\vdots& &\vdots&\vdots& &{\vdots} &\ddots& \\ -\eta &-\eta &{\cdots} & 1 & 1 &\cdots& -\eta &\cdots&r-s \end{bmatrix} \begin{bmatrix} y_{1} \\ y_{2} \\ {\vdots} \\ y_{j} \\ y_{j+1} \\ {\vdots} \\ y_{s} \\ {\vdots} \\ y_{r} \end{bmatrix}\!\leq\! \begin{bmatrix} 1 \\ 1 \\ {\vdots} \\ 1 \\ 1 \\ {\vdots} \\ 1 \\ {\vdots} \\ 1 \end{bmatrix} \end{array} $$

Lemma 4

L({u₁,u₂,⋯ ,u_s− 1}) ≥ L({u₁,u₂,⋯ ,u_s}) for any s = 1, 2,⋯ ,r.

Proof

We abbreviate L({u₁,u₂,⋯ ,u_s}) as L_s for simplicity. Let c_j = u_s. When y_j > 0, an optimal solution for LP L_s has the following form $Y_{s}^{*} = \{y_{1},\cdots , y_{j-1}, y_{j}, y_{j}, y_{j}\frac {r-s+\eta }{r-s}, \cdots , y_{j} (\frac {r-s+\eta }{r-s})^{r-j-1} \}$. We construct a feasible solution Y_s− 1 of L_s− 1. Suppose the first j elements of Y_s− 1 are consistent with the first j elements of $Y_{s}^{*}$, then Y_s− 1 can be expressed as $\{ y_{1},\cdots , y_{j-1}, y_{j}, y_{j}\frac {r-s+\eta +1}{r-s+1}, \cdots , y_{j}(\frac {r-s+\eta +1}{r-s+1})^{r-j} \}$. We can obtain $L^{*}_{s}- L_{s-1}= y_{j}+ y_{j}\frac {r-s+\eta }{r-s}+ \cdots + y_{j} (\frac {r-s+\eta }{r-s})^{r-j-1} - y_{j}\frac {r-s+\eta +1}{r-s+1}- \cdots - y_{j}(\frac {r-s+\eta +1}{r-s+1})^{r-j} = y_{j}[1- \frac {r-s+\eta +1}{r-s+1}] +{\cdots } + y_{j}[(\frac {r-s+\eta }{r-s})^{r-j-1} -(\frac {r-s+\eta +1}{r-s+1})^{r-j}] \leq 0$. When y_j = 0, the form of the optimal solution of LP L_s can be written as $Y_{s}^{*} = \{y_{1},\cdots , y_{j-1}, 0, y_{j-1}\frac {r-s+\eta +1}{r-s},$ $y_{j-1}\frac {r-s+\eta +1}{r-s} \frac {r-s+\eta }{r-s}, \cdots , y_{j-1}\frac {r-s+\eta +1}{r-s} (\frac {r-s+\eta }{r-s})^{r-j-1} \}$. Similarly, let the first j − 1 items of Y_s− 1 be consistent with the first j − 1 items of $Y_{s}^{*}$, then Y_s− 1 can be expressed as $\{y_{1},\cdots , y_{j-1}, y_{j-1}\frac {r-s+\eta +1}{r-s+1}, \cdots , y_{j-1} (\frac {r-s+\eta +1}{r-s+1})^{r-j+1} \}$. Then $L^{*}_{s}- L_{s-1} \leq 0$. Hence, L({u₁,u₂,⋯ ,u_s− 1}) ≥ L({u₁,u₂,⋯ ,u_s}) for any s = 1, 2,⋯ ,r. □

Theorem 8

Given that C is the solution obtained by the greedy algorithm, Opt is the optimal solution of MIE-c, which satisfies

$$ F(C) \leq \frac{1-{\varrho}^F}{{\varrho}^F}[e^{\frac{{\varrho}^F}{1-{\varrho}^F}} -1] F(Opt). $$

where ϱ^F is the supermodular curvature of set function F.

Proof

From LP (A1), it can be inferred that F(C) ≤ F(Opt) ⋅ L({u₁,⋯ ,u_s}) for any s = 1,⋯ ,r. By lemma 4, we can obtain $L(\{ u_{1}, \cdots , u_{s}\}) \leq L(\{ u_{1}, \cdots , u_{s-1}\}) \leq {\cdots } \leq L(\varnothing )$. Hence, $F(C) \leq F(Opt)\cdot L(\varnothing )$. When $\overline {Opt} \bigcap \overline {C}= \varnothing$, based on LP (A1), we can derive $L(\varnothing )= \frac {1}{r} + \frac {r+\eta }{r \cdot r}+{\cdots } + \frac {(r+\eta )^{j}}{r \cdot r^{j}} +{\cdots } + \frac {(r+\eta )^{r-1}}{r \cdot r^{r-1}} = \frac {1}{\eta } [\frac {(r+\eta )^{r}}{r^{r}} -1] = \frac {1}{\eta } [(1+\frac {\eta }{r})^{r} -1] \leq \frac {1}{\eta } [e^{\eta } -1]$. Let $\eta = \frac {{\varrho }^{F}}{1-{\varrho }^{F}}$, and the theorem is proved immediately. □