Decentralized probabilistic density control of autonomous swarms with safety constraints

Abstract

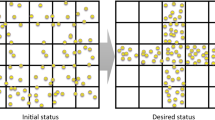
This paper presents a Markov chain based approach for the probabilistic density control of a large number, swarm, of autonomous agents. The proposed approach specifies the time evolution of the probabilistic density distribution by using a Markov chain, which guides the swarm to a desired steady-state distribution, while satisfying the prescribed ergodicity, motion, and safety constraints. This paper generalizes our previous results on density upper bound constraints and captures a general class of linear safety constraints that bound the flow of agents. The safety constraints are formulated as equivalent linear inequality conditions on the Markov chain matrices by using the duality theory of convex optimization which is our first contribution. With the safety constraints, we can facilitate proper low-level conflict avoidance policies to compute and execute the detailed agent state trajectories. Our second contribution is to develop (i) linear matrix inequality based offline methods, and (ii) quadratic programming based online methods that can incorporate these constraints into the Markov chain synthesis. The offline method provides a feasible solution for Markov matrix when there is no density feedback. The online method utilizes realtime estimates of the swarm density distribution to continuously update the Markov matrices to maximize the convergence rates within the problem constraints. The paper also introduces a decentralized method to compute the density estimates needed for the online synthesis method.

Appendix: Two interpretations of the probabilistic swarm distribution

The following lemma provides two interpretations for the swarm distribution x(t): (i) x(t) is the vector of expected ratios of the agents in each bin; (ii) the ensemble of agent states, $\{r_k(t)\}_{k=1}^N$, has a distribution that approaches x(t) with probability one as N is increased towards infinity.

Lemma 2

Consider N agents where $x_1(0)=\cdots =x_N(0) = x_0 \in {\mathbb {P}}^m$ with $x_k, \ k= 1,2,\ldots ,$ defined as in (1). Further, suppose that each agent uses the PDC algorithm with the same Markov matrix M(t), that is, $M_1(t) = \cdots =M_N(t)=M(t)$. Then, $x_1(t) = \cdots = x_N(t) = x(t)$ for $t=0,1,\ldots ,$ where

$$\begin{aligned}&x(t+1) = M(t)x(t), \quad \text{ with } \ x(0) = x_0, \ \mathrm{and} \end{aligned}$$

(33)

$$\begin{aligned}&x[i](t) = \mathrm{prob}(r(t) \in R_i ) = {\mathbb {E}}\left( \frac{\mathbf{n}[i](t) }{N}\right) , \quad i=1,\ldots ,m,\nonumber \\ \end{aligned}$$

(34)

$\mathrm{prob}(r(t) \in R_i )$ is the probability of finding an agent in the ith bin, and $\mathbf{n}(t)$ is the vector of the number of agent states in each bin at t. Furthermore,

$$\begin{aligned} \mathrm{prob}\left( \lim _{N \rightarrow \infty }\frac{\mathbf{n}(t)}{N}= x (t) \right) = 1, \quad t=0,1,\ldots . \end{aligned}$$

(35)

Proof

It is straight forward to show that (3) implies (33) by using the the Total Probability theorem (Chung 2001) and noting that $\mathrm{prob}(r(t+1) \in R_i) = \sum _{j=1}^m \mathrm{prob}(r(t+1) \in R_i|\mathrm{prob}(r(t) \in R_j)) \mathrm{prob}(r(t)\in R_j).$ Since the PDC algorithm uses the same Markov matrix for each agent at each time, $M_1(t)=\cdots =M_N (t)=M(t)$ with $x_1(0)=\cdots =x_M(0)=x(0)$, the probability distribution of all agents evolves according to (33). Clearly $\mathrm{prob}(r(t) \in R_i )$ is the probability of finding any of the agents in ith bin. Since ${\mathbb {E}}(\mathbf{n}[i](t)) = \sum _{k=1}^N x_k[i](t)= N x[i](t)$, we have $x(t)={\mathbb {E}}(\mathbf{n}(t)/N)$.

Next, we prove (35) by using standard arguments as in Theorem 5.4.2 of Chung (2001). Consider x[i](t) which is the probability of finding any agent in bin i at time t. Consider a new Random Variable (RV), $Z_k[i](t)$, such that $Z_k[i](t) =1$ if agent k is in bin i at time t, and zero otherwise. Clearly, ${\mathbb {E}}(Z_k[i](t)) = x_k[i](t)=x[i](t)$ and $Z_k[i](t), \ k=1,\ldots ,N,$ form Independently Identically Distributed (iid) RVs. Then it follows that $\mathbf{n}[i](t) =Z_1[i](t) +\ldots + Z_N[i](t)$. Since $Z_k[i](t), \ k=1,\ldots ,N$ are iid RVs and $\mathrm{E}[| Z_k[i](t)|] < \infty$, we can use the strong law of large numbers theorem, Chung (2001, Theorem 5.4.2), to conclude, $\mathrm{prob}\left( \lim _{N \rightarrow \infty } \frac{\mathbf{n}[i](t)}{N} = x[i] (t) \right) = 1,$ which implies (35). $\square$