A distributed control and parameter estimation protocol with prescribed performance for homogeneous lagrangian multi-agent systems

Abstract

In this paper, we consider the formation control problem for uncertain homogeneous Lagrangian nonlinear multi-agent systems in a leader-follower scheme under a directed communication protocol. A distributed adaptive control protocol of minimal complexity is proposed that achieves prescribed, arbitrarily fast and accurate formation establishment as well as synchronization of the parameter estimates of all followers. The estimation and control laws are distributed in the sense that the control signal and the update laws are calculated based solely on local relative state information. Moreover, provided that the communication graph is strongly connected and contrary to the related works on multi-agent systems, the controller-imposed transient and steady state performance bounds are fully decoupled from: (i) the underlying graph topology, (ii) the control gains selection and (iii) the agents’ model uncertainties. Finally, extensive simulation studies on the attitude control of flying spacecrafts clarify and verify the approach.

1 Introduction

Multi-agent systems have recently emerged as an inexpensive and robust way of addressing a wide variety of tasks ranging from exploration, surveillance, and reconnaissance to cooperative construction and manipulation. The success of these systems relies on efficient information exchange and coordination among team members. More specifically, their intriguing feature hinges on the fact that each agent makes decisions solely on the basis of its local perception. Thus, a challenging task is to design a distributed control approach for certain global goals in the presence of limited information exchange. In this direction, drawing some insight from biological observations, distributed cooperative control of multi-agent systems has received considerable attention during the last two decades [see the seminal works (Jadbabaie et al. 2003; Fax and Murray 2004; Olfati-Saber and Murray 2004; Ren and Beard 2005) for example]. In particular, the leader-follower formation scheme, according to which the following agents aim at creating a rigid formation with the leader’s state, employing only locally available information, has recently become very popular, since in the absence of any central control system and without global coordinate information, following a leader is an accountable motivation.

Although the majority of the works on distributed cooperative control consider known and simple dynamical models, many practical engineering systems exist that fail to satisfy that assumption. Hence, taking into account the inherent model uncertainties when designing distributed control schemes is of paramount importance. However, extending towards this direction the existing control techniques for ideal models, such as linear control theory (Jadbabaie et al. 2003; Fax and Murray 2004; Olfati-Saber and Murray 2004; Ren and Beard 2005), $\mathcal {H}_{\infty }$ control (Trentelman et al. 2013; Liu and Lunze 2014; Ugrinovskii 2014; Peymani et al. 2015), energy function method (Yu et al. 2016, 2017) or internal model principal (Wieland et al. 2011; Xiang et al. 2013; Su and Huang 2014; Seyboth et al. 2015), becomes a very challenging task on account of the increasing design complexity, owing to the interacting system dynamics as reflected by the local intercourse specifications. In order to handle the model uncertainties, a variety of control approaches such as adaptive synchronization (Chung et al. 2009; Dong 2011; Chen and Lewis 2011; Liu et al. 2014; Zhang and Demetriou 2014, 2015), sliding mode control (Mei et al. 2011; Cao and Ren 2012; Yang et al. 2013), pinning control (Yu et al. 2010; Song et al. 2010) and neural network based control (Hou et al. 2009; Cheng et al. 2010; Das and Lewis 2010; Zhang and Lewis 2012; Yoo 2013; El-Ferik et al. 2014; Shen and Shi 2015) have been proposed. Moreover, in homogeneous multi robot systems, distributed adaptive algorithms with the agents collaborating in order to enhance the update scheme and rapidly synchronize their parameter estimates were presented in Nestinger and Demetriou (2012) and Sadikhov et al. (2014).

An issue of utmost importance associated with distributed control schemes for multi-agent systems concerns the transient and steady state response of the closed loop system. Traditionally, the neighborhood error is proven to converge within a residual set, whose size depends on control design parameters and some unknown (though bounded) terms. In particular, owing to the fact that the state of the leader is not accessible to all followers,¹ the dynamics of the leader acts inherently as unknown and bounded disturbance within the dynamics of the overall multi-agent system. However, no systematic procedure exists to accurately compute the required upper bounds, thus making the a priori selection of the control gains to satisfy certain steady state behavior practically impossible. Moreover, it is difficult to analytically establish transient behavior (i.e., the convergence rate) as it is heavily affected by the agents’ dynamics and and the status of the overall underlying interaction topology, both of which are considered unknown. The transient performance problem was first relaxed for single integrator and 1st order nonlinear multi-agent systems under undirected communication graphs in Karayiannidis et al. (2012) and Bechlioulis and Kyriakopoulos (2014, 2015), following the notion of prescribed performance control (Bechlioulis and Rovithakis 2008). Recently, a distributed prescribed performance synchronization protocol was presented in Bechlioulis and Rovithakis (2016) for high order nonlinear multi-agent systems, which however cannot be applied for the problem confronted herein since the input gain matrix is considered non-diagonal and state dependent.

In this paper,² a generic class of homogeneous Lagrangian nonlinear multi-agent systems under a directed communication protocol is considered. A distributed adaptive formation control scheme is designed in the sense that each agent utilizes only local relative state information from its neighborhood set to calculate its own control signal and update its parameters’ estimate, without incorporating any prior knowledge of the parameters of the model dynamics. Additionally, the imposed transient and steady state response bounds are solely pre-determined by certain designer-specified performance functions and are fully decoupled by the agents’ dynamical model, the underlying graph topology and the control gains selection, facilitating further the control design procedure.

The concepts and techniques of prescribed performance control methodology, which were recently developed in Bechlioulis and Rovithakis (2008, 2010, 2014) for uncertain nonlinear systems, are innovatively adapted in this work to deal with the distributed formation control problem of unknown Lagrangian nonlinear multi-agent systems. In this direction, it is stressed that in all original works, the proposed controllers were designed in a centralized manner owing to the fact that full state feedback was incorporated. Hence, since decentralization is essential in this work, i.e., each agent should operate solely on the basis of its local/neighborhood feedback, our previous results cannot be straightforwardly applied in the considered control problem, owing to the interacting system dynamics that are reflected by the local intercourse specifications; thus rendering the contribution of this paper with respect to Bechlioulis and Rovithakis (2008, 2010, 2014) considerable.

The remainder of this article is structured as follows. Section 2 formulates the problem. The main results are presented in Sect. 3. Extensive simulation studies that clarify and verify the approach are given in Sect. 4. Finally, conclusions are drawn in Sect. 5.

1.1 Notation

The n-th dimensional Euclidean space is denoted by $\mathfrak {R}^{n}$. The set of all non-negative real numbers is signified by $\mathfrak {R}_{+}$. The set of all $n\times m$ real matrices is represented by $\mathfrak {R}^{n\times m}$. The absolute value of a scalar $a\in \mathfrak {R}$ and the Euclidean norm of a vector $\varvec{a} \in \mathfrak {R}^{n}$ are denoted by $\left| a\right|$ and $\left\| \varvec{a}\right\|$, respectively. Furthermore, the notations $\left[ a_{i}\right]$ and $\left[ a_{ij}\right]$ imply the vector and the matrix with the corresponding elements. Given a positive definite matrix A, $\lambda _{\min }\left( A\right)$ and $\lambda _{\max }\left( A\right)$ denote its minimum and maximum eigenvalues. Similarly, $\sigma _{\min }\left( A\right)$ denotes the minimum singular value of a matrix A. The function $\mathrm {diag}\left( \varvec{a}\right)$, where $\varvec{a} \triangleq \left[ a_{i}\right]$ is an n-th dimensional vector, denotes the $n\times n$ diagonal matrix of the elements of $\varvec{a}$. Finally, $\underline{\mathbf {1}}\in \mathfrak {R}^{n}$ represents the n-th dimensional vector with all elements equal to one and $\otimes$ denotes the Kronecker product.

2 Problem formulation

Consider a multi-agent group comprising of a leader and N identical followers, with the leading agent acting as an exosystem that generates a desired command/reference trajectory for the multi-agent group. The following agents obey a common Lagrangian nonlinear dynamical model, described by:

$$\begin{aligned} M\left( x_{i}\right) \ddot{x}_{i}+C\left( x_{i},\dot{x}_{i}\right) \dot{x}_{i}+D\left( \dot{x}_{i}\right) +G\left( x_{i}\right) =\tau _{i}\text {, }i=1,\dots ,N \end{aligned}$$

(1)

where $x_{i}\in \mathfrak {R}^{P}$, $\dot{x}_{i}\in \mathfrak {R}^{P}$ and $\tau _{i}\in \mathfrak {R}^{P}$, $i=1,\dots ,N$ denote the states and the control input of each agent and $M\left( \cdot \right) \in \mathfrak {R}^{P\times P}$, $C\left( \cdot ,\cdot \right) \in \mathfrak {R}^{P\times P}$, $D\left( \cdot \right) \in \mathfrak {R}^{P}$, $G\left( \cdot \right) \in \mathfrak {R}^{P}$ model the inertia, the coriolis, the viscous friction and the gravitational effects, respectively.

Property 1

The uncertain physical parameters of the agents appear linearly in the dynamical model (1). Hence, we may express the dynamics in terms of a set of unknown but constant parameters $\theta \in \mathfrak {R}^{Q}$ in the following way:

$$\begin{aligned} {M}\left( a\right) {d+C}\left( a,b\right) c{+D} \left( b\right) {+G}\left( a\right) {=Z}\left( a,b,c,d\right) {\theta } \end{aligned}$$

(2)

where $Z\left( a,b,c,d\right)$ is a $P\times Q$ regressor matrix, composed of smooth known nonlinear functions. $\square$

Property 2

The inertia and the coriolis matrices satisfy the following skew-symmetric property:

$$\begin{aligned} \xi ^{T}\left( \dot{M}-2C\right) \xi =0, \, \forall \xi \in \mathfrak {R}^{P}. \end{aligned}$$

$\square$

A directed graph (digraph) $\mathcal {G}=\left( \mathcal {V},\mathcal {E} \right)$ is used to model the communication among the followers, where $\mathcal {V}=\left\{ v_{1},\dots ,v_{N}\right\}$ denotes the set of vertices that represent each agent. The set of edges is denoted as $\mathcal {E} \subseteq \mathcal {V}\times \mathcal {V}$ and the graph is assumed to be simple, i.e. $\left( v_{i},v_{i}\right) \notin \mathcal {E}$ (there exist no self loops). The adjacency matrix associated with the digraph $\mathcal {G}$ is denoted as $A=\left[ a_{ij}\right] \in \mathfrak {R}^{N\times N}$ with $a_{ij} \in \left\{ 0,1\right\}$, $i,j=1,\dots ,N$. If $a_{ij}=1$ then the agent i obtains information regarding the state of the j-th agent (i.e., $\left( v_{i},v_{j}\right) \in \mathcal {E}$), whereas if $a_{ij}=0$ then there is no state-information flow from agent j to agent i (i.e., $\left( v_{i},v_{j}\right) \notin \mathcal {E}$). Furthermore, the set of neighbors of a vertex $v_{i}$ is denoted by $\mathcal {N}_{i}=\left\{ v_{j}:\left( v_{i},v_{j}\right) \in \mathcal {E}\right\}$ and the degree matrix is defined as ${\varDelta }=\mathrm {diag}\left( \left[ {\varDelta }_{i}\right] \right) \in \mathfrak {R}^{N\times N}$ with ${\varDelta }_{i}=\sum _{j\in \mathcal {N}_{i}}a_{ij}$. In this respect, the Laplacian matrix of the graph is denoted by $L={\varDelta }-A\in \mathfrak {R}^{N\times N}$. Additionally, the state of the leader node (labeled $v_{0}$) is given by $x_{0}:\mathfrak {R}_{+}\rightarrow \mathfrak {R}^{P}$ and is further assumed to be smooth and bounded. However, the desired command/reference trajectory information is only provided to a subgroup of the N agents. The access of the following agents to the leader’s state is modeled by a diagonal matrix $A_{0}=\mathrm {diag}\left( \left[ a_{i0}\right] \right) \in \mathfrak {R}^{N\times N}$. If $a_{i0}$, $i\in \left\{ 1,2,\dots ,N\right\}$ is equal to 1, then the i-th agent obtains state information from the leader node; otherwise if $a_{i0}$, $i\in \left\{ 1,2,\dots ,N\right\}$ equals to 0, then the i-th agent cannot obtain state information from the leader node. In this way, the augmented digraph is denoted by $\mathcal {\bar{G}}=\left( \mathcal {\bar{V}},\mathcal {\bar{E}}\right)$, where $\mathcal {\bar{V}}=\mathcal {V}\cup \left\{ v_{0}\right\}$ and $\mathcal {\bar{E}}=\mathcal {E}\cup \left\{ \left( v_{i},v_{0}\right) :a_{i0}=1\right\} \subseteq \mathcal {\bar{V}}\times \mathcal {\bar{V}}$ and the augmented set of neighbors is defined as $\mathcal {\bar{N}}_{i}=\left\{ v_{j}:\left( v_{i},v_{j}\right) \in \mathcal {\bar{E}}\right\}$, $i=1,\dots ,N$.

In the sequel, we formulate the distributed control and parameter estimation problem for the aforementioned multi-agent system that will be confronted herein.

Problem: Design a distributed control and parameter estimation protocol for the following agents that obey the uncertain dynamics (1) as well as Properties 1 and 2, such that they create a constant feasible [in the sense of Dimarogonas and Kyriakopoulos (2008)] formation, described by the desired relative offsets³ $c_{ij}\in \mathfrak {R}^{P}$, $i=1,\dots ,N$ with respect to each member $j\in \left\{ 0,1,\dots ,N\right\}$ of their augmented fixed and a priori known communication set $\mathcal {\bar{N}}_{i}$. Additionally, the desired formation should be achieved within a predetermined transient period and be maintained with predefined arbitrary accuracy in the steady state.

To solve the aforementioned multi-agent problem, the following assumption is required on the underlying communication graph topology.

Assumption A

The communication graph $\mathcal {G}$ is strongly connected and balanced and at least one of the followers can get access to the leader state.

Remark 1

The strong connectivity of the considered communication digraph $\mathcal {G}$ implies that information from any followers flows either directly or indirectly to all other followers. In this way, the relative formation control problem with respect to the leader becomes feasible. In the same spirit, information accrued by the distributed estimation protocols is dissipated in the multi-agent system, thus enhancing the distributed learning in case of a persistently exciting leader motion. On the other hand, the assumption on the balanced property of the underlying graph can be easily relaxed by initially applying a decentralized algorithm for balancing strongly connected digraphs (Priolo et al. 2013).

Notice that Assumption A dictates that the matrix $L+A_{0}$ is a nonsingular $\mathcal {M}$-matrix⁴ (Shivakumar and Chew 1974). Finally, the following technical lemma regarding nonsingular $\mathcal {M}$-matrices will be employed to derive the main results of this work.

Lemma 1

Qu (2009) Consider a nonsingular $\mathcal {M}$-matrix $W\in \mathfrak {R}^{N\times N}$. There exists a diagonal positive definite matrix $P=\left( \mathrm {diag}\left( q\right) \right) ^{-1}$, with $q=W^{-1}\underline{1}$, such that $PW+W^{T}P\in \mathfrak {R}^{N\times N}$ is also positive definite.

3 Distributed control and parameter estimation

Since only local relative state information is considered available, the control law of each agent should be based on the neighborhood error feedback:

$$\begin{aligned} e_{i}=\sum _{j\in \mathcal {\bar{N}}_{i}}a_{ij}\left( x_{i}-x_{j}+c_{ij}\right) \in \mathfrak {R}^{P}\text {, }i=1,\dots ,N, \end{aligned}$$

(3)

where $c_{ij}$ for $i=1,\dots ,N$ and $j\in \mathcal {\bar{N}}_{i}$, denote the relative offsets that define the desired feasible formation. Moreover, let us also define the overall neighborhood error vector as $\bar{e}=\left[ e_{1}^{T},\dots ,e_{N}^{T}\right] ^{T}\in \mathfrak {R}^{NP}$, which, employing the graph topology and after some trivial algebraic manipulations, becomes:

$$\begin{aligned} \bar{e}=\left( L+A_{0}\right) \otimes I_{P}\left( \bar{x}-\bar{x}_{0} +\bar{c}\right) \end{aligned}$$

(4)

where $\bar{x}\triangleq \left[ x_{1}^{T},\dots ,x_{N}^{T}\right] \in \mathfrak {R}^{NP}$ is the overall state vector of the multi-agent system, $\bar{x}_{0} \triangleq \left[ x_{0}^{T},\dots ,x_{0}^{T}\right] ^{T}\in \mathfrak {R}^{NP}$ and

$$\begin{aligned} \bar{c}=\left( \left( L+A_{0}\right) \otimes I_{P}\right) ^{-1}\left[ \begin{array}[c]{c} {\sum }_{j\in \mathcal {\bar{N}}_{1}}c_{1j}\\ \vdots \\ {\sum }_{j\in \mathcal {\bar{N}}_{N}}c_{Nj} \end{array} \right] =\left[ \begin{array} [c]{c} c_{1}\\ \vdots \\ c_{N} \end{array} \right] \end{aligned}$$

(5)

denotes the relative offset $c_{i}\in \mathfrak {R}^{P}$ of the i-th agent, $i=1,\dots ,N$ with respect to the leader, as dictated by the desired formation. In this way, the desired formation is expressed with respect to the leader’s state, thus it is achieved when the state $x_{i}$ of each agent approaches the leader’s state $x_{0}$ with the corresponding offset $c_{i}$, $i=1,\dots ,N$. Hence, defining the disagreement formation variable as $\bar{\delta }\triangleq \left[ \delta _{1}^{T},\dots ,\delta _{N}^{T}\right] ^{T}=\bar{x}-\bar{x}_{0}+\bar{c}$, the formation control problem is solved if the disagreement errors $\delta _{i}$, $i=1,\dots ,N$ converge to a small neighborhood of the origin. However, the disagreement formation variables $\delta _{i}$, $i=1,\dots ,N$ involve global information knowledge. In particular, notice that they involve information directly from the leader⁵ as well as from the whole graph topology through the inverse of $\left( L+A_{0}\right) \otimes I_{P}$ that is employed in (5) to extract the relative offsets with respect to the leader $c_{i}\in \mathfrak {R}^{P}$, $i=1,\dots ,N$. Therefore, they cannot be measured in a distributed sense, based on the local intercourse specifications. Nevertheless, observing (4) and utilizing the non-singularity of $L+A_{0}$ owing to Assumption A, we obtain:

$$\begin{aligned} \left\| \bar{\delta }\right\| \le \frac{\left\| \bar{e}\right\| }{\sigma _{\min }\left( L+A_{0}\right) } \end{aligned}$$

(6)

from which we conclude that the neighborhood error $\bar{e}$ may represent a valid metric of the formation quality.

Since the state of the leader is not available to all agents, asymptotic convergence of the disagreement formation variables $\delta _{i}$, $i=1,\dots ,N$ to the origin is quite challenging owing to the fact that the dynamics of the leader act as unknown disturbances within the dynamics of the overall multi agent system. Additionally, the size of the corresponding achieved ultimate bounds would depend on certain control design parameters and the unknown bounds of the leader’s state. However, no systematic procedure exists to accurately compute the required upper bounds in a distributed manner, thus making the a priori selection of the aforementioned control parameters to satisfy certain steady state behavior, practically impossible. Moreover, it is difficult to analytically establish transient behavior (i.e., the convergence rate) as it is heavily affected by the agents’ dynamics and and the status of the overall underlying interaction topology, both of which are considered unknown.

To alleviate the aforementioned issues, we propose to adopt the prescribed performance control technique that was originally employed to design centralized controllers utilizing full state feedback, for various classes of nonlinear systems (Bechlioulis and Rovithakis 2008, 2010, 2014). Prescribed performance characterizes the behavior where the error converges to a predefined arbitrarily small residual set with convergence rate no less than a certain predefined value and is achieved if the error evolves strictly within a predefined region that is bounded by certain functions of time, called performance functions. Thus, selecting for each neighborhood error $e_{i}\triangleq \left[ e_{i1},e_{i2},\dots ,e_{iP}\right] ^{T}$ the corresponding exponential performance functions $\rho _{i}\left( t\right) \triangleq \left[ \rho _{i1}\left( t\right) ,\rho _{i2}\left( t\right) ,\dots ,\rho _{iP}\left( t\right) \right] ^{T}$ with $\rho _{ij}\left( t\right) =\left( \rho _{ij0}-\rho _{\infty }\right) e^{-lt}$ $+\rho _{\infty }$ for $i=1,\dots ,N$ and $j=1,\dots ,P$, such that: (i) $\left| e_{ij}\left( 0\right) \right| <\rho _{ij0}$ and (ii) the parameters l, $\rho _{\infty }$ incorporate the desired transient and steady state specifications respectively, it can easily be verified that the solution of the prescribed performance control problem for all neighborhood errors (i.e., enforcing $\left| e_{ij}\left( t\right) \right| <\rho _{ij}\left( t\right)$, $\forall t\ge 0$, $i=1,\dots ,N$ and $j=1,\dots ,P$) leads directly to the solution of the multi-agent control problem confronted herein. More specifically, notice from (6) that guaranteeing $\left| e_{ij}\left( t\right) \right| <\rho _{i,j}\left( t\right)$, $\forall t\ge 0$, imposes explicit exponential convergence of the disagreement errors $\delta _{i}$, $i=1,\dots ,N$ to the residual set ${\varDelta }=\left\{ \delta \in \mathfrak {R}^{P}:\left\| \delta \right\| \le \frac{\sqrt{NP}\rho _{\infty }}{\sigma _{\min }\left( L+A_{0}\right) }\right\}$ with rate l. Although $\sigma _{\min }\left( L+A_{0}\right)$ is a global topology variable and thus cannot be employed in distributed control schemes, we might use a conservative lower bound:

$$\begin{aligned} \frac{\left( \frac{N-1}{N}\right) ^{\frac{N-1}{2}}}{N^{2} +N-1}\le \sigma _{\min }\left( L+A_{0}\right) , \end{aligned}$$

as presented in Hong and Pan (1992), that depends on the number of agents N and not on the graph topology. Alternatively, a distributed power iteration estimation algorithm (Sabattini et al. 2014) could initially be applied to estimate $\sigma _{\min }\left( L+A_{0}\right)$.

In the sequel, we propose a distributed control and parameter estimation protocol that guarantees $\left| e_{ij}\left( t\right) \right| < \rho _{ij}\left( t\right)$, $\forall t\ge 0$, $i=1,\dots ,N$ and $j=1,\dots ,P$ and achieves estimation consensus.

Theorem 1

Consider the multi-agent system (1) with a communication graph topology satisfying Assumption A. Given the neighborhood errors $e_{i}$, $i=1,\dots ,N$ as defined in (3) and the appropriately selected corresponding performance functions $\rho _{i}\left( t\right)$, $i=1,\dots ,N$, that encapsulate the desired transient and steady state specifications, the following distributed control and parameter estimation scheme:

$$\begin{aligned} v_{d_{ij}}&=-\tfrac{\left( \tfrac{2K_{p_{i}}}{\rho _{ij}\left( t\right) }\right) }{1-\left( \frac{e_{ij}}{\rho _{ij}\left( t\right) }\right) ^{2} }\ln \left( \tfrac{1+\frac{e_{ij}}{\rho _{ij}\left( t\right) }}{1-\frac{e_{ij}}{\rho _{ij}\left( t\right) }}\right) \text {, }j=1,\dots ,P \end{aligned}$$

(7a)

$$\begin{aligned} s_{i}&=\dot{x}_{i}-v_{di}\text { with }v_{di}\triangleq \left[ v_{d_{i1} },\dots ,v_{d_{iP}}\right] ^{T} \end{aligned}$$

(7b)

$$\begin{aligned} \tau _{i}&=Z\left( x_{i},\dot{x}_{i},v_{d_{i}},\dot{v}_{d_{i}}\right) ^{T}\hat{\theta }_{i}-K_{v_{i}}s_{i} \end{aligned}$$

(7c)

$$\begin{aligned} \dot{\hat{\theta }}_{i}&=-{\varGamma }_{i}\left( Z\left( x_{i},\dot{x}_{i},v_{d_{i}},\dot{v}_{d_{i}}\right) s_{i}+\gamma \sum _{j\in \mathcal {N}_{i} }a_{ij}\left( \hat{\theta }_{i}-\hat{\theta }_{j}\right) \right) \end{aligned}$$

(7d)

with $K_{p_{i}},K_{v_{i}},{\varGamma }_{i},\gamma >0$ and $Z\left( x_{i},\dot{x} _{i},v_{d_{i}},\dot{v}_{d_{i}}\right)$ denoting the regressor matrix from Property 1, guarantees $\left| e_{ij}\left( t\right) \right| <\rho _{ij}\left( t\right)$, $\forall t\ge 0$ and $\lim _{t\rightarrow \infty }\left\| \hat{\theta }_{i}\left( t\right) -\hat{\theta }_{l}\left( t\right) \right\| =0$ for $i,l=1,\dots ,N$, $j=1,\dots ,P$ as well as the boundedness of all closed loop signals.

Proof

Let us first define the normalized errors $\xi _{i}\triangleq \left[ \xi _{i1},\dots ,\xi _{iP}\right] ^{T}$, $i=1,\dots ,N$ with:

$$\begin{aligned} \xi _{ij}=\tfrac{e_{ij}}{\rho _{ij}\left( t\right) }\text {, }i=1,\dots ,N\text { and }j=1,\dots ,P \end{aligned}$$

(8)

as well as the overall state vector:

$$\begin{aligned} \varvec{\xi }=\left[ \xi _{1}^{T},\dots ,\xi _{N}^{T},s^{T},\tilde{\theta }^{T}\right] ^{T}, \end{aligned}$$

where $s\triangleq \left[ s_{1}^{T},\dots ,s_{N}^{T}\right] ^{T}$ and $\tilde{\theta }\triangleq \left[ \tilde{\theta }_{1}^{T},\dots ,\theta _{N} ^{T}\right] ^{T}$denote the overall vectors of the velocity errors $s_{i}=\dot{x}_{i}-v_{di}$ and the parameter errors $\tilde{\theta } _{i}=\hat{\theta }_{i}-\theta$, $i=1,\dots ,N$ respectively. Differentiating the normalized errors (8), the velocity errors $s_i$, $i=1,\dots ,N$ as well as the parametric errors $\tilde{\theta }_{i}$, $i=1,\dots ,N$ with respect to time and employing (1), (4) as well as the control and parameter estimation protocol (7a)–(7d), we obtain in a compact form, the closed loop dynamical system:

$$\begin{aligned} \varvec{\dot{\xi }}=h\left( t,\varvec{\xi }\right) \end{aligned}$$

(9)

where the function $h\left( t,\varvec{\xi }\right)$ involves the terms of the model dynamics as well as those of the proposed scheme. Let us also define the set ${\varOmega }_{\varvec{\xi }}=\underbrace{\left( -1,1\right) \times \cdots \times \left( -1,1\right) }_{NP\text {-times}} \times {\varOmega }_{s}\times {\varOmega }_{\theta }$, where ${\varOmega }_{s}=\left\{ s\in \mathfrak {R}^{NP}:\left\| s\right\| <\bar{s}\right\}$ and ${\varOmega }_{\theta }=\left\{ \tilde{\theta }\in \mathfrak {R}^{NQ}:\right.$ $\left. \left\| \tilde{\theta }\right\| <\bar{\theta }\right\}$ are open sets with $\bar{s}$, $\bar{\theta }$ denoting positive constants that will be specified later for analysis purposes only. In the sequel, we proceed in two phases. First, the existence and uniqueness of a maximal solution $\varvec{\xi }\left( t\right)$ of (9) over the set ${\varOmega }_{\varvec{\xi }}$ for a time interval $\left[ 0,\tau _{\max }\right)$ is ensured (i.e., $\varvec{\xi }\left( t\right) \in {\varOmega }_{\varvec{\xi }}$, $\forall t\in \left[ 0,\tau _{\max }\right)$). Then, we prove that the proposed control scheme guarantees, for all $t\in \left[ 0,\tau _{\max }\right)$: (a) the boundedness of all closed loop signals of (9) as well as that (b) $\varvec{\xi }\left( t\right)$ remains strictly within a compact subset of ${\varOmega }_{\varvec{\xi }}$, which subsequently will lead by contradiction to $\tau _{\max }=\infty$ and consequently to the solution of the multi-agent problem confronted herein.

Phase 1: Notice that the set ${\varOmega }_{\varvec{\xi }}$ is nonempty and open. Moreover, owing to the selection of the initial value of the performance functions (i.e., $\left| e_{ij}\left( 0\right) \right| <\rho _{ij}\left( 0\right)$) we conclude that $\varvec{\xi }\left( 0\right) \in {\varOmega }_{\varvec{\xi }}$ for certain positive constants $\bar{s}$, $\bar{\theta }$ satisfying $\left\| s\left( 0\right) \right\| <\bar{s}$ and $\left\| \tilde{\theta }\left( 0\right) \right\| <\bar{\theta }$ respectively. Additionally, owing to the smoothness of: (a) the system nonlinearities, (b) the desired trajectory and (c) the proposed control and parameter estimation scheme over ${\varOmega }_{\varvec{\xi }}$, it can easily be verified that $h\left( t,\varvec{\xi }\right)$ is continuous on t and continuous for all $\varvec{\xi }\in {\varOmega }_{\varvec{\xi }}$. Therefore, the hypotheses of Theorem 54 (pp. 476) in Sontag (1998) hold and the existence and uniqueness of a maximal solution $\varvec{\xi }\left( t\right)$ of (9) on a time interval $\left[ 0,\tau _{\max }\right)$ such that $\varvec{\xi }\left( t\right) \in {\varOmega }_{\varvec{\xi }}$, $\forall t\in \left[ 0,\tau _{\max }\right)$ is ensured. Equivalently, we deduce that:

$$\begin{aligned} \xi _{ij}\left( t\right) \in \left( -1,1\right) \text {, }i=1,\dots ,N\text { and }j=1,\dots ,P \end{aligned}$$

(10)

and $\left\| s\left( t\right) \right\| <\bar{s}$, $\left\| \tilde{\theta }\right\| <\bar{\theta }$ for all $t\in \left[ 0,\tau _{\max }\right)$. Thus, the signals $\varepsilon _{i}\left( t\right) \triangleq \left[ \varepsilon _{i1}\left( t\right) ,\dots ,\varepsilon _{iP}\left( t\right) \right] ^{T}$, $i=1,\dots ,N$ with

$$\begin{aligned} \varepsilon _{ij}\left( t\right) =\ln \left( \tfrac{1+\xi _{ij}\left( t\right) }{1-\xi _{ij}\left( t\right) }\right) \text {, }i=1,\dots ,N\text { and }j=1,\dots ,P \end{aligned}$$

(11)

are well defined for all $t\in \left[ 0,\tau _{\max }\right)$. Moreover, from Assumption A, $L+A_{0}$ and consequently $\left( L+A_{0}\right) \otimes I_{P}$ are nonsingular $\mathcal {M}$-matrices. Hence, the product $\left( \left( L+A_{0}\right) \otimes I_{P}\right) K_{p}$ with $K_{p}\triangleq \mathrm {diag}\left( \left[ K_{p_{i}}\right] \right) \otimes I_{P}$ is also a nonsingular $\mathcal {M}$-matrix owing to the fact that $K_{p}$ is diagonal with positive entries.⁶ Therefore, invoking Lemma 1, there exists a diagonal positive definite matrix P defined as $P=\left( \mathrm {diag}\left( q\right) \right) ^{-1}$ with $q=\left( \left( \left( L+A_{0}\right) \otimes I_{P}\right) K_{p}\right) ^{-1}\underline{1}$ such that ${{P\left( \left( L+A_{0}\right) \otimes I_{P}\right) K_{p}+K_{p}\left( \left( L+A_{0}\right) \otimes I_{P}\right) }}^{T}{{P}}$ is a positive definite matrix.

Phase 2: To proceed, consider the positive definite function:

$$\begin{aligned} V_{1}=\frac{1}{2}\varepsilon ^{T}P\varepsilon \end{aligned}$$

where $\varepsilon \triangleq \left[ \varepsilon _{1}^{T} ,\dots ,\varepsilon _{N}^{T}\right] ^{T}$. Differentiating $V_{1}$ with respect to time and employing (4), we obtain:

$$\begin{aligned} {{\dot{V}_{1}=\varepsilon ^{T}P}}\varvec{r}{{\left( \left( \left( L+A_{0}\right) \otimes I_{P}\right) \left( \dot{\bar{x}}-\dot{\bar{x}}_{0}\right) -\dot{\rho }_{\xi }\right) }} \end{aligned}$$

where $\varvec{r}\triangleq \mathrm {diag}\left( \left[ \tfrac{\left( \frac{2}{\rho _{ij}\left( t\right) }\right) }{1-\xi _{ij}^{2}}\right] \right)$ and

$$\begin{aligned} \dot{\rho }_{\xi }\triangleq \left[ \left( \mathrm {diag}\left( \left[ \dot{\rho }_{1j}\left( t\right) \right] \right) \xi _{1}\right) ^{T},\dots ,\left( \mathrm {diag}\left( \left[ \dot{\rho }_{Nj}\left( t\right) \right] \right) \xi _{N}\right) ^{T}\right] ^{T}. \end{aligned}$$

Invoking the diagonality of P and $\varvec{r}$, adding and subtracting $\varepsilon ^{T}\varvec{r}P\left( \left( L+A_{0}\right) \otimes I_{P}\right) v_{d}$ with $v_{d}\triangleq \left[ v_{d_{1}}^{T},\dots ,v_{d_{N}}^{T}\right] ^{T}$ and substituting $v_{d_{i}}$, $i=1,\dots ,N$ from the control protocol, we get:

$$\begin{aligned} {{\dot{V}_{1}=-\varepsilon ^{T}}}\varvec{r}{{P\left( \left( L+A_{0}\right) \otimes I_{P}\right) K_{p}}}\varvec{r} {{\varepsilon +\varepsilon ^{T}}}\varvec{r}{{F}} \end{aligned}$$

(12)

where the term $F\triangleq {{P}}\left( \left( \left( L+A_{0}\right) \otimes I_{P}\right) \left( s-\dot{\bar{x}}_{0}\right) -\dot{\rho }_{\xi }\right)$ satisfies $\left\| F\right\| \le \bar{F}$, $\forall t\in \left[ 0,\tau _{\max }\right)$ for a positive constant $\bar{F}$ independent of $\tau _{\max }$, owing to: (i) equation (10), (ii) the fact that $\dot{\rho }_{ij}\left( t\right)$, $\dot{\bar{x}}_{0}$ are bounded by construction and by assumption and (iii) $\left\| s\left( t\right) \right\| <\bar{s}$, $\forall t\in \left[ 0,\tau _{\max }\right)$. Expanding ${{P\left( \left( L+A_{0}\right) \otimes I_{P}\right) K_{p}}}$ in its symmetric and skew-symmetric part, it is deduced that:

$$\begin{aligned} {{\dot{V}_{1}=-}}\tfrac{1}{2}{{\varepsilon ^{T}}}\varvec{rQr} {{\varepsilon +\varepsilon ^{T}}}\varvec{r}{{F}} \end{aligned}$$

where ${\varvec{Q}\triangleq {{P\left( \left( L+A_{0}\right) \otimes I_{P}\right) K_{p}+K_{p}\left( \left( L+A_{0}\right) \otimes I_{P}\right) }}^{T}{{P}}}$ is positive definite from Lemma 1. Therefore, $\dot{V}_{1}<0$ when $\left\| \varepsilon \right\| >\frac{\bar{F}\max \left\{ \left[ \rho _{ij}\left( 0\right) \right] \right\} }{\lambda _{\min }\left( \varvec{Q}\right) }$. Thus, it is concluded that:

$$\begin{aligned} \left\| \varepsilon \left( t\right) \right\| \le \bar{\varepsilon }\triangleq \max \left\{ \left\| \varepsilon \left( 0\right) \right\| ,\tfrac{\bar{F}\max \left\{ \left[ \rho _{ij}\left( 0\right) \right] \right\} }{\lambda _{\min }\left( \varvec{Q}\right) }\sqrt{\tfrac{\lambda _{\max }\left( P\right) }{\lambda _{\min }\left( P\right) }}\right\} \end{aligned}$$

(13)

for all $t\in \left[ 0,\tau _{\max }\right)$, which from (11), by applying the inverse logarithmic function, leads to:

$$\begin{aligned} -1<\tfrac{\exp \left( -\bar{\varepsilon }\right) -1}{\exp \left( -\bar{\varepsilon }\right) +1}=\underline{\xi }\le \xi _{ij}\left( t\right) \le \overline{\xi }=\tfrac{\exp \left( \bar{\varepsilon }\right) -1}{\exp \left( \bar{\varepsilon }\right) +1}<1 \end{aligned}$$

(14)

for all $t\in \left[ 0,\tau _{\max }\right)$. Consequently, all $v_{d_{i}}$, $i=1,\dots ,N$ also remain bounded for all $t\in \left[ 0,\tau _{\max }\right)$.

In the sequel, let us consider the following positive definite function:

$$\begin{aligned} V_{2}=\tfrac{1}{2}\sum _{i=1}^{N}s_{i}^{T}Ms_{i}+\tfrac{1}{2}\sum _{i=1} ^{N}\tilde{\theta }_{i}^{T}{\varGamma }_{i}^{-1}\tilde{\theta }_{i} \end{aligned}$$

that involves the velocity and parameter errors $s_{i}\triangleq \dot{x}_{i}-v_{d_i}$, $\tilde{\theta }_{i}\triangleq \hat{\theta }_{i}-\theta$, $i=1,\dots ,N$. Differentiating $V_{2}$ with respect to time, we obtain:

$$\begin{aligned} \dot{V}_{2}=\sum _{i=1}^{N}s_{i}^{T}M\left( \ddot{x}_{i}-\dot{v}_{d_{i} }\right) +\tfrac{1}{2}\sum _{i=1}^{N}s_{i}^{T}\dot{M}s_{i}+\sum _{i=1}^{N}\tilde{\theta }_{i}^{T}{\varGamma }_{i}^{-1}\dot{\hat{\theta }}_{i}\text {.} \end{aligned}$$

Adding and subtracting the term $\sum _{i=1}^{N}s_{i}^{T}Cs_{i}$ and employing the dynamics of the agents (1) as well as Properties 1 and 2, we conclude:

$$\begin{aligned} \dot{V}_{2} =&\sum _{i=1}^{N}s_{i}^{T}\left( \tau _{i}-Z\left( x_{i},\dot{x}_{i},v_{d_{i}},\dot{v}_{d_{i}}\right) ^{T}\hat{\theta }_{i}\right) \\&\left. +\sum _{i=1}^{N}s_{i}^{T}Z\left( x_{i},\dot{x}_{i},v_{d_{i}} ,\dot{v}_{d_{i}}\right) ^{T}\tilde{\theta }_{i}\right. \left. +\sum _{i=1}^{N}\tilde{\theta }_{i}^{T}{\varGamma }_{i}^{-1}\dot{\hat{\theta }}_{i}\right. . \end{aligned}$$

Substituting the proposed distributed control and parameter estimation protocol, expanding $L\otimes I_{Q}$ in its symmetric and skew-symmetric part and employing Assumption A,⁷ we arrive at:

$$\begin{aligned} \dot{V}_{2}&=-\sum _{i=1}^{N}s_{i}^{T}K_{v_{i}}s_{i} - \gamma \sum _{i=1}^{N}\tilde{\theta }_{i}^{T}\sum _{j\in \mathcal {N}_{i}}a_{ij}\left( \hat{\theta }_{i}-\hat{\theta }_{j}\right) \nonumber \\&=-\sum _{i=1}^{N}s_{i}^{T}K_{v_{i}}s_{i}-\gamma \tilde{\theta }^{T}\left( L\otimes I_{Q}\right) \tilde{\theta } \end{aligned}$$

(15)

$$\begin{aligned}&=-\sum _{i=1}^{N}s_{i}^{T}K_{v_{i}}s_{i}-\tfrac{1}{2}\gamma \tilde{\theta }^{T}\left( \left( L\otimes I_{Q}\right) +\left( L\otimes I_{Q}\right) ^{T}\right) \tilde{\theta }\le 0\text {.} \end{aligned}$$

(16)

which guarantees the boundedness of $s_{i}$, $\tilde{\theta }_{i}$, $i=1,\dots ,N$ and consequently of the proposed distributed control and parameter estimation protocol for all $t\in \left[ 0,\tau _{\max }\right)$. Thus, there exist positive constants $\bar{s}^{\prime }$ and $\bar{\theta }^{\prime }$ such that $s\left( t\right) \in {\varOmega }_{\varvec{s}}^{^{\prime }}\triangleq \left\{ s\in \mathfrak {R}^{NP}:\left\| s\right\| <\bar{s}^{\prime }\right\}$ and $\tilde{\theta }\left( t\right) \in {\varOmega }_{\theta }^{\prime }\triangleq \left\{ \tilde{\theta }\in \mathfrak {R}^{NQ} :\left\| \tilde{\theta }\right\| <\bar{\theta }^{\prime }\right\}$, $\forall t\in \left[ 0,\tau _{\max }\right)$ respectively.

Up to this point, what remains to be shown is that $\tau _{\max }=\infty$. In this direction, notice that $\varvec{\xi }\left( t\right) \in {\varOmega }_{\varvec{\xi }}^{^{\prime }}$, $\forall t\in \left[ 0,\tau _{\max }\right)$, where:

$$\begin{aligned} {\varOmega }_{\varvec{\xi }}^{^{\prime }}= {\displaystyle \prod } \left[ \tfrac{\exp \left( -\bar{\varepsilon }\right) -1}{\exp \left( -\bar{\varepsilon }\right) +1},\tfrac{\exp \left( \bar{\varepsilon }\right) -1}{\exp \left( \bar{\varepsilon }\right) +1}\right] _{NP\text {-times}} \times {\varOmega }_{\varvec{s}}^{^{\prime }}\times {\varOmega }_{\theta }^{\prime } \end{aligned}$$

is a nonempty and compact set. Moreover, it can easily be verified that ${\varOmega }_{\varvec{\xi }}^{^{\prime }}\subset {\varOmega }_{\varvec{\xi }}$ for any $\bar{s}$, $\bar{\theta }$ satisfying $\bar{s}^{^{\prime }}<\bar{s}$ and $\bar{\theta }^{\prime }<\bar{\theta }$. Hence, assuming $\tau _{\max }<\infty$ and since ${\varOmega }_{\varvec{\xi }}^{^{\prime }}\subset {\varOmega }_{\varvec{\xi }}$, Proposition C.3.6 (pp. 481) in Sontag (1998) dictates the existence of a time instant $t^{^{\prime }}\in \left[ 0,\tau _{\max }\right)$ such that $\varvec{\xi }\left( t^{^{\prime }}\right) \notin {\varOmega }_{\varvec{\xi }}^{^{\prime }}$, which is a clear contradiction. Therefore, $\tau _{\max } =\infty$. As a result, all closed loop signals remain bounded and moreover $\varvec{\xi }\left( t\right) \in {\varOmega }_{\varvec{\xi }}^{^{\prime } }\subset {\varOmega }_{\varvec{\xi }}$, $\forall t\ge 0$. Furthermore, from (14), we conclude that:

$$\begin{aligned} -\rho _{ij}\left( t\right)<\tfrac{\exp \left( -\bar{\varepsilon }\right) -1}{\exp \left( -\bar{\varepsilon }\right) +1}\rho _{ij}\left( t\right) \le e_{ij}\left( t\right) \le \tfrac{\exp \left( \bar{\varepsilon }\right) -1}{\exp \left( \bar{\varepsilon }\right) +1}\rho _{ij}\left( t\right) <\rho _{ij}\left( t\right) \end{aligned}$$

(17)

for all $i=1,\dots ,N$, $j=1,\dots ,P$ and $t\ge 0$. Additionally, invoking Barbalat’s Lemma for the positive definite function $V_{2}$, which was proven to be non-increasing (see 16) and obtains a uniformly continuous time derivative (notice that $\ddot{V}_{2}$ is bounded owing to the boundedness of $\dot{s}_{i}$, $\dot{\hat{\theta }}_{i}$, $i=1,\dots ,N$), we conclude that $\lim _{t\rightarrow \infty }\dot{V}_{2}\left( t\right) =0$. Therefore, from (15) it is deduced that $\lim _{t\rightarrow \infty }s_{i}\left( t\right) =0$, $i=1,\dots ,N$ and $\lim _{t\rightarrow \infty }\left\| \left( L\otimes I_{Q}\right) \tilde{\theta }\right\| =0$, from which the convergence of $\tilde{\theta }$ to the null space of the $L\otimes I_{Q}$ matrix is extracted. However, it should be noted that the eigenvector that spans the null space of $L\otimes I_{Q}$, where L is a Laplacian matrix of a strongly connected and balanced graph, is of the form $\left[ \theta _{\star }^{T},\dots ,\theta _{\star }^{T}\right] ^{T}\in \mathfrak {R}^{NQ}$ with $\theta _{\star }\in \mathfrak {R}^{Q}$; hence all $\tilde{\theta }_{i}\left( t\right) =\hat{\theta }_{i}\left( t\right) -\theta$, $i=1,\dots ,N$ converge to the same value, yielding thus $\lim _{t\rightarrow \infty }\left\| \hat{\theta }_{i}-\hat{\theta }_{l}\right\| =0$, for all $i,l=1,\dots ,N$, which completes the proof. $\square$

3.1 Remarks

Design philosophy The prescribed performance control technique guarantees the predefined transient and steady state performance specifications, that are encapsulated in the corresponding performance functions $\rho _{ij}\left( t\right)$, $i=1,\dots ,N$ and $j=1,\dots ,P$, by enforcing the normalized errors $\xi _{ij}\left( t\right)$ to remain strictly within the set $\left( -1,1\right)$ for all $t\ge 0$. Notice that by modulating $\xi _{ij}\left( t\right)$ via the logarithmic function $\ln \left( \tfrac{1+\star }{1-\star }\right)$ in the control signal $v_{d_{ij}}$ and selecting $\rho _{ij}\left( 0\right) >\left| e_{ij}(0)\right|$, the control signals $\varepsilon _{ij}(t)$, as defined in (11), are initially well defined. Moreover, it is not difficult to verify that simply maintaining the boundedness of the modulated errors $\varepsilon _{ij}(t)$ for all $t\ge 0$ is equivalent to guaranteeing $\xi _{ij}\left( t\right) \in \left( -1,1\right)$ for all $t\ge 0$. Therefore, the problem at hand can be visualized as stabilizing the modulated errors $\varepsilon _{ij}(t)$ within the feasible regions defined via $\xi _{ij}\in \left( -1,1\right)$ for all $t\ge 0$. A careful inspection of $v_{d_{ij}}$ in the proposed control scheme reveals that it actually operates similarly to barrier functions in constrained optimization, admitting high negative or positive values depending on whether $e_{ij}\left( t\right) \rightarrow -\rho _{ij}\left( t\right)$ or $e_{ij}\left( t\right) \rightarrow \rho _{ij}\left( t\right)$, respectively; eventually preventing $e_{ij}\left( t\right)$ from reaching the corresponding boundaries imposed by the appropriately selected performance functions $\rho _{ij}\left( t\right)$.

Robust prescribed performance From the proof of the aforementioned theorem, it can be deduced that the proposed control and parameter estimation scheme achieves the desired formation with prescribed transient and steady state performance for the considered class of Lagrangian multi-agent systems, without resorting to the need of rendering the ultimate bound $\bar{\varepsilon }$ of the modulated formation error vector $\varepsilon \left( t\right)$ arbitrarily small, by adopting extreme values of the control gains $K_{p_{i}}$, $K_{v_{i}}$ (see 13). More specifically, notice that (14) and consequently (17), which enforces prescribed performance, hold no matter how large the finite bound $\bar{\varepsilon }$ is. In the same spirit, high velocity profiles of the leader (i.e., $\dot{x}_{0}\left( t\right)$) can be compensated as they affect only the size of F in (12), but leave unaltered the achieved stability properties. Hence, the closed loop multi-agent system response, which is solely determined by the performance functions $\rho _{i}\left( t\right)$, $i=1,\dots ,N$, becomes isolated against uncertainties and greatly extends the robustness of the proposed scheme. Furthermore, contrary to the standard distributed control schemes for static graphs, whose convergence rate is dictated by the connectivity level (i.e., the smallest singular value of $L+A_{0}$), the transient response of the proposed scheme is independent of the underlying topology as long as Assumption A holds.

Fig. 1

The undirected communication topology among the following and the leading spacecrafts. The arrows represent the information flow

Fig. 2

Proposed scheme–Scenario 1: the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$ (red, green, blue lines) along with the imposed performance bounds (black dashed lines) (Color figure online)

Fig. 3

Proposed scheme–Scenario 1: the evolution of the norm of the parameter estimate vectors $\theta _{i}\left( t\right)$, $i=1,\dots ,6$

Fig. 4

Proposed scheme–Scenario 1: the required control input signals $\tau _{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

Fig. 5

Adaptive synchronization approach (Chung et al. 2009)–Scenario 1: the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

Fig. 6

Adaptive synchronization approach (Chung et al. 2009)–Scenario 1:the required control input signals $\tau _{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

Design complexity Unlike what is common practice in the related literature, the response is explicitly and solely determined by appropriately selecting the parameters l, $\rho _{\infty }$ of the performance functions $\rho _{ij}\left( t\right)$, $i=1,\dots ,N$ and $j=1,\dots ,P$. In particular, the decreasing rate l directly introduces a lower bound on the speed of convergence of the neighborhood error e $_{ij}$. Furthermore, $\rho _{\infty } =\lim _{t\rightarrow \infty }\rho _{ij}\left( t\right)$ regulates the maximum allowable error at steady state. However, it should be noted that the agents do not have to adopt common values for the convergence rate l and the ultimate limit $\rho _{\infty }$ of the corresponding performance functions. Apparently, different convergence rates and ultimate limits will achieve different transient and steady state response for each member of the team, but yet, the overall achieved response will be dictated by the minimum and maximum adopted values of the convergence rate and the ultimate limit of the performance functions. Therefore, the “common” information that should be shared in the multi-agent team is the minimum required convergence rate and the maximum steady state error, which do not raise in practise any significant issue on the decentralized nature of the proposed scheme. In that respect, the attributes of the performance functions $\rho _{ij}\left( t\right)$ are selected a priori, in accordance to the desired transient and steady state performance specifications. Additionally, an extra condition concerning the initial value of the performance functions has to be satisfied (i.e., $\rho _{ij}\left( 0\right) >\left| e_{ij}\left( 0\right) \right|$). Nevertheless, it is stressed that the initial value of the performance functions does not affect either their transient or their steady state properties as mentioned earlier. Moreover, since $e_{ij}\left( t\right)$, $i=1,\dots ,N$ depend solely on the available state of the neighboring agents, the aforementioned condition can be easily satisfied by selecting the initial value of the corresponding performance functions $\rho _{ij}\left( 0\right)$ to be greater than $\left| e_{ij}\left( 0\right) \right|$. It is underlined however that the proposed controller does not guarantee either the quality of the evolution of the neighborhood errors $e_{ij}\left( t\right)$ inside the performance envelopes or the control input characteristics (magnitude and slew rate). In this direction, extensive simulation studies have revealed that the selection of the control gains $K_{p_{i}}$, $K_{v_{i}}$ can have positive influence (e.g., decreasing the gain values leads to increased oscillatory behaviour within the prescribed performance envelope described by (17), which is improved when adopting higher values, enlarging, however, the control effort both in magnitude and rate). Thus, an additional fine tuning might be needed in real scenarios to retain the required control input signals within the feasible range that can be implemented by the actuators.⁸ Similarly, the control input constraints impose an upper bound on the required speed of convergence of $\rho _{ij}\left( t\right)$ as obtained by the exponential $\exp \left( -lt\right)$ as well as the velocity profile of the leader. Nevertheless, an upper bound of the term F in (12), which is related to the velocity profile of the leader and the desired performance specifications, as well as an upper bound of the unknown dynamic parameters of (1) should be given in order to extract any relationships between the achieved performance and the input constraints.⁹ Finally, the numerical complexity of the proposed scheme is kept low since it involves very few and simple calculations to deliver the control signal (i.e., P calculations of the $\ln (\cdot )$ function, one calculation of the regressor matrix $Z(\cdot ,\cdot ,\cdot ,\cdot )$, $4P+2Q$ scalar additions, $3P+\left| \mathcal {N}_{i}\right| +1$ scalar multiplications and 4 vector multiplications). Similarly, the update laws, which provide the parameter estimates $\hat{\theta }_i$, $i=1,\dots ,N$ and have to be solved online, are numerically stable and raise no significant issue during their integration for appropriately selected parameters $\gamma$ and ${\varGamma }_i$, $i=1,\dots ,N$.

Persistence of excitation The proposed distributed parameter estimation scheme may exhibit learning capabilities in the aforementioned adaptive control framework as long as a Persistence of Excitation condition [see Section 5.6 in Khalil (1992)] can be verified for the regressor matrix $Z\left( x_{i},\dot{x}_{i},\dot{x}_{d_{i}},\ddot{x}_{d_{i}}\right)$, $i=1,\dots ,N$. Therefore, all parameter estimates $\hat{\theta }_{i}$, $i=1,\dots ,N$ will eventually converge to their actual values $\theta$ and the system achieves learning in a distributed way. Notice that the information accrued by the distributed estimation protocols will be dissipated in the multi-agent system as long as Assumption A holds for the underlying communication graph, enhancing thus the learning process, in contrast to the conventional adaptive estimation approaches, where estimation protocols that are fully-independent and with no interconnections are employed.

Fig. 7

Sliding mode control approach (Yang et al. 2013)–Scenario 1: the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

Fig. 8

Sliding mode control approach (Yang et al. 2013)–Scenario 1: the required control input signals $\tau _{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

4 Simulation results

We consider six identical flying spacecrafts with the following attitude¹⁰ dynamics (Markley and Crassidis 2014) expressed in the body frame:

$$\begin{aligned} J\dot{\omega }_{i}-\left( J\omega _{i}\right) \times \omega _{i}=u_{i}\text {, }i=1,\dots ,6 \end{aligned}$$

(18)

where $J\in \mathfrak {R}^{3\times 3}$ is the common positive definite inertia matrix and $\omega _{i},u_{i}\in \mathfrak {R}^{3}$ denote the angular velocity and the control torque of each spacecraft, respectively. The moments of inertia in each axis of the body frame, that are involved in J, are considered unknown and thus have to be estimated online (the actual values of the moments of inertia used for simulation purposes are $J_{xx}=4$, $J_{xy}=J_{yx}=0.5$, $J_{xz} =J_{zx}=0.25$, $J_{yy}=3.5$, $J_{yz}=J_{zy}=0.35$, $J_{zz}=4.5$). Moreover, to extract the aforementioned dynamics in a compatible form with the Lagrangian dynamics (1) presented in this work, the attitude of the spacecrafts will be expressed in the Modified Rodrigues parametrization (Shuster 1993) as:

$$\begin{aligned} q_{i}\triangleq \left[ q_{i1},q_{i2},q_{i3}\right] ^{T}\triangleq \varvec{e} _{i}\tan \frac{\theta _{i}}{4} \end{aligned}$$

where $\varvec{e}_{i}\in \mathfrak {R}^{3}$ is the eigenaxis unit vector and $\theta _{i}\in \left( -\,2\pi ,2\pi \right)$ is the eigenangle that parameterize the attitude of each spacecraft. Then, the attitude kinematics can be written as:

$$\begin{aligned} \dot{q}_{i}=Z\left( q_{i}\right) \omega _{i} \end{aligned}$$

(19)

where

$$\begin{aligned} Z\left( q_{i}\right) =\frac{1}{2}\left( \left( \frac{1-q_{i}^{T}q_{i}}{2}\right) I_{3}+q_{i}q_{i}^{T}+S\left( q_{i}\right) \right) \end{aligned}$$

and the skew-symmetric matrix $S\left( q_{i}\right)$ is defined as:

$$\begin{aligned} S\left( q_{i}\right) =\left[ \begin{array} [c]{ccc} 0 &{} -q_{i3} &{} q_{i2}\\ q_{i3} &{} 0 &{} -q_{i1}\\ -q_{i2} &{} q_{i1} &{} 0 \end{array} \right] \text {.} \end{aligned}$$

Combining (18) and (19), the attitude dynamics may be expressed in the Lagrangian form as follows:

$$\begin{aligned} M\left( q_{i}\right) \ddot{q}_{i}+C\left( q_{i},\dot{q}_{i}\right) \dot{q}_{i}=\tau _{i} \end{aligned}$$

(20)

where

$$\begin{aligned} M\left( q_{i}\right) =&Z^{-T}\left( q_{i}\right) JZ^{-1}\left( q_{i}\right) \\ C\left( q_{i},\dot{q}_{i}\right) =&-Z\left( q_{i}\right) ^{-T} JZ^{-1}\left( q_{i}\right) \dot{Z}\left( q_{i}\right) Z^{-1}\left( q_{i}\right) \\&-Z^{-T}\left( q_{i}\right) S\left( q_{i}\right) JZ^{-1}\left( q_{i}\right) \\ \tau _{i} =&Z^{-T}\left( q_{i}\right) u_{i} \end{aligned}$$

Finally, it can easily be verified after straightforward algebraic manipulations that $M\left( q_{i}\right)$ is a positive definite matrix, $\dot{M}\left( q_{i}\right) -2C\left( q_{i},\dot{q}_{i}\right)$ is a skew-symmetric matrix and the left side of (20) can be linearly parameterized with respect to the unknown moments of inertia involved in J.

To demonstrate the proposed distributed control and parameter estimation protocol and point out its intriguing performance attributes with respect to existing results in the related literature, a comparative simulation study with the control protocols reported in Chung et al. (2009) (adaptive attitude synchronization) and Yang et al. (2013) (sliding mode control) was conducted. Further simulation studies under persistence of excitation demonstrated how learning (i.e., convergence of the parameter estimates to their actual values) is affected by the information that is dissipated in the multi-agent system. Eventually, it was verified that the learning process is enhanced by the distributed estimation protocol compared to a conventional adaptive estimation approach, in which fully-independent and with no interconnections update algorithms are employed at each agent.

Fig. 9

The directed communication topology among the following and the leading spacecrafts. The arrows represent the information flow

Fig. 10

Adaptive synchronization approach (Chung et al. 2009)–Scenario 2: the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

4.1 Comparative study

In the first scenario, we consider a slow command/reference trajectory (leader node):

$$\begin{aligned} q_{d}\left( t\right) =\left[ \begin{array} [c]{c} \sin \left( \frac{\pi }{6}\sin \left( 0.1t\right) \right) \cos \left( \frac{\pi }{6}\cos \left( 0.1t\right) \right) \\ \sin \left( \frac{\pi }{6}\sin \left( 0.1t\right) \right) \sin \left( \frac{\pi }{6}\cos \left( 0.1t\right) \right) \\ \cos \left( \frac{\pi }{6}\sin \left( 0.1t\right) \right) \end{array} \right] \tan \left( \frac{\pi }{4}\right) \end{aligned}$$

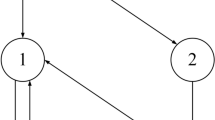
which represents an attitude reference frame that forms a cone with aperture $\frac{\pi }{6} \ \mathrm {rads}$ on the unit sphere. Moreover, the underlying communication topology is described by an undirected connected graph that is depicted in Fig. 1 and is defined by the following augmented neighboring sets $\bar{N}_{1}=\left\{ 0,2,6\right\}$, $\bar{N}_{2}=\left\{ 1,3\right\}$, $\bar{N}_{3}=\left\{ 2,4\right\}$, $\bar{N}_{4}=\left\{ 0,3,5\right\}$, $\bar{N}_{5}=\left\{ 4,6\right\}$, $\bar{N}_{6}=\left\{ 1,5\right\}$. Finally, the control objective is to achieve attitude synchronization with minimum speed of convergence as obtained by the exponential $\exp \left( -\,\frac{4t}{25}\right)$ and maximum steady state errors 0.01 (i.e., the errors should approach a small neighborhood of the origin within 25 s). In this direction, exponential performance functions are selected to encapsulate the aforementioned performance specifications, and the control gains are set as $K_{p}=1$, $K_{v}=4$, ${\varGamma }=0.06$, $\gamma =1$ to yield smooth error evolution within the desired performance envelopes and reasonable control effort. Finally, the initial estimates of the unknown moments of inertia deviate up to 50% from their actual values.

Fig. 11

Sliding mode control approach (Yang et al. 2013)–Scenario 2: the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$

Fig. 12

Proposed scheme–Scenario 2: the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$ (red, green, blue lines) along with the imposed performance bounds (black dashed lines) (Color figure online)

Fig. 13

Proposed scheme–Scenario 2: the required control input signals $\tau _{i}\left( t\right) \in \mathfrak {R}^{3}, i=1,\dots ,6$

The simulation results of the proposed control and parameter estimation protocol are depicted in Figs. 2–4. In particular, Fig. 2 illustrates the evolution of the neighborhood errors $e_{i}\left( t\right) \in \mathfrak {R}^{3}$, $i=1,\dots ,6$ along with the associated transient and steady state performance specifications encapsulated by the corresponding performance functions. The evolution of the norm of the parameter estimate vectors $\theta _{i}\left( t\right) , i=1,\dots ,6$ is given in Fig. 3 and the required control input signals are provided in Fig. 4. As it was predicted by the theoretical analysis, the attitude synchronization control problem was solved and the desired performance specifications were satisfied with bounded control signals and despite the parametric uncertainty. Satisfactory results were also obtained by employing both the adaptive synchronization approach (Chung et al. 2009) (see Figs. 5, 6) as well as the sliding mode control approach (Yang et al. 2013) (see Figs. 7, 8). However, in order to achieve the desired transient and steady state performance, the corresponding control gains were selected via a tedious trial and error procedure.

In the second scenario, we considered a faster reference profile (the frequency was set 10 times larger than in the previous case):

$$\begin{aligned} q_{d}\left( t\right) =\left[ \begin{array} [c]{c} \sin \left( \frac{\pi }{6}\sin \left( t\right) \right) \cos \left( \frac{\pi }{6}\cos \left( t\right) \right) \\ \sin \left( \frac{\pi }{6}\sin \left( t\right) \right) \sin \left( \frac{\pi }{6}\cos \left( t\right) \right) \\ \cos \left( \frac{\pi }{6}\sin \left( t\right) \right) \end{array} \right] \tan \left( \frac{\pi }{4}\right) \end{aligned}$$

as well as a less connected directed communication topology (see Fig. 9) defined by the following augmented neighboring sets $\bar{N}_{1}=\left\{ 0,6\right\}$, $\bar{N}_{2}=\left\{ 1\right\}$, $\bar{N}_{3}=\left\{ 2\right\}$, $\bar{N}_{4}=\left\{ 3\right\}$, $\bar{N}_{5}=\left\{ 4\right\}$, $\bar{N}_{6}=\left\{ 5\right\}$. It should be noticed that without altering the control gains of the previous simulation scenario, the performance of both approaches in Chung et al. (2009) and Yang et al. (2013) degraded significantly as shown in Figs. 10 and 11, respectively. On the contrary, as observed in Figs. 12 and 13, the proposed distributed control and parameter estimation scheme with unaltered control gain values preserved the performance quality despite the faster velocity profile of the leader and the less communicated topology. In this way, it is verified that the achieved performance is fully decoupled from the underlying graph topology, the control gains selection and the parametric uncertainty, and it is solely prescribed by the appropriate selection of the corresponding performance functions.

4.2 Persistence of excitation

In this simulation study, we consider a persistently exciting reference trajectory (leader node) that involves six sinusoidal terms with various frequencies and amplitudes. Initially, we adopted a conventional adaptive approach to estimate the unknown parameters (i.e., we set $\gamma =0$ in the proposed scheme to model no interconnections among the adaptive laws). The results are given in Fig. 14. Notice that after 180 s all parameter estimates have converged to their actual values. Subsequently, we adopted the proposed distributed parameter estimation approach with $\gamma =1$. In this case, notice in Fig. 15 that all parameter estimates have attained their actual value after 100 s, which indicates that the learning process is enhanced in the proposed approach by the information being dissipated in the multi-agent system.

Fig. 14

Conventional adaptive estimation approach: the colored lines illustrate the estimation of each unknown parameter, whereas the black dotted line depicts its actual value (Color figure online)

Fig. 15

Proposed distributed estimation approach: the colored lines illustrate the estimation of each unknown parameter, whereas the black dotted line depicts its actual value (Color figure online)

5 Conclusions

A distributed control and parameter estimation protocol was proposed for uncertain homogeneous Lagrangian nonlinear multi-agent systems in a leader-follower scheme, that achieves and maintains arbitrarily fast and accurately a rigid formation with the leader as well as synchronization of the parameter estimates. The developed scheme exhibits the following important characteristics. First, it is distributed in the sense that the control signal and the parameter estimates of each agent are calculated on the basis of local relative state information from its neighborhood set. Moreover, its complexity is proved to be considerably low. Very few and simple calculations are required to output the control signal. Additionally, no prior knowledge of the agents’ parameters of the dynamic model is required. Furthermore, the achieved prescribed transient and steady state performance, which is independent of the underlying graph topology and is explicitly imposed by designer-specified performance functions, significantly simplifies the control gains selection.

Future research efforts will be devoted towards addressing the collision avoidance and connectivity maintenance problems as well as the case where the agents do not share information expressed in a commonly agreed frame within a similar framework (i.e., robustness, prescribed transient and steady state performance), which would significantly increase its applicability in mobile multi-agent systems.