Abstract
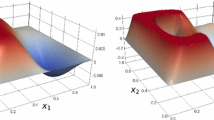
In the present work, we apply a variational discretization proposed by the first author in (Comput. Optim. Appl. 30:45–61, 2005) to Lavrentiev-regularized state constrained elliptic control problems. We extend the results of (Comput. Optim. Appl. 33:187–208, 2006) and prove weak convergence of the adjoint states and multipliers of the regularized problems to their counterparts of the original problem. Further, we prove error estimates for finite element discretizations of the regularized problem and investigate the overall error imposed by the finite element discretization of the regularized problem compared to the continuous solution of the original problem. Finally we present numerical results which confirm our analytical findings.
Similar content being viewed by others
References
Alibert, J.-J., Raymond, J.-P.: Boundary control of semilinear elliptic equations with discontinuous leading coefficients and unbounded controls. Numer. Funct. Anal. Optim. 18, 235–250 (1997)
Bergounioux, M., Ito, K., Kunisch, K.: Primal-dual strategy for constrained optimal control problems. SIAM J. Control Optim. 37, 1176–1194 (1999)
Bergounioux, M., Kunisch, K.: Primal-dual active set strategy for state-constrained optimal control problems. Comput. Optim. Appl. 22, 193–224 (2002)
Bergounioux, M., Kunisch, K.: On the structure of the Lagrange multiplier for state-constrained optimal control problems. Syst. Control Lett. 48, 169–176 (2002)
Casas, E.: L 2 estimates for the finite element method for the Dirichlet problem with singular data. Numer. Math. 47, 627–632 (1985)
Casas, E.: Control of an elliptic problem with pointwise state constraints. SIAM J. Control Optim. 24, 1309–1317 (1986)
Casas, E.: Boundary control of semilinear elliptic equations with pointwise state constraints. SIAM J. Control Optim. 31, 993–1006 (1993)
Dauge, M.: Elliptic Boundary Value Problems on Corner Domains: Smoothness and Asymptotics of Solutions. Lecture Notes Math., vol. 1341. Springer, Berlin (1988)
Deckelnick, K., Hinze, M.: Convergence of a finite element approximation to a state constrained elliptic control problem. SIAM J. Numer. Anal. 45, 1937–1953 (2007)
Deckelnick, K., Hinze, M.: A finite element approximation to elliptic control problems in the presence of control and state constraints. Preprint HBAM2007-01, Hamburger Beiträge zur Angewandten Mathematik, Universität Hamburg (2007)
Deckelnick, K., Hinze, M.: Numerical analysis of a control and state constrained elliptic control problem with piecewise constant control approximations. Preprint HBAM2007-02, Hamburger Beiträge zur Angewandten Mathematik, Universität Hamburg (2007), to appear in Proceedings of the ENUMATH 2007 in Graz
Hintermüller, M., Kunisch, K.: Path following methods for a class of constrained minimization methods in function spaces. SIAM J. Optim. 17, 159–187 (2006)
Hintermüller, M., Kunisch, K.: Feasible and non-interior path following in constrained minimization with low multiplier regularity. SIAM J. Control Optim. 45, 1198–1221 (2006)
Hinze, M.: A variational discretization concept in control constrained optimization: the linear quadratic case. Comput. Optim. Appl. 30, 45–61 (2005)
Meyer, C.: Optimal control of semilinear elliptic equations with applications to sublimation crystal growth. PhD thesis, Department of Mathematics, Technical University Berlin (2006)
Meyer, C.: Error estimates for the finite-element approximation of an elliptic control problem with pointwise state and control constraints. Control Cybern. 37, 51–85 (2008)
Meyer, C., Prüfert, U., Tröltzsch, F.: On two numerical methods for state-constrained elliptic control problems. Optim. Meth. Softw. 22, 871–899 (2007)
Meyer, C., Rösch, A., Tröltzsch, F.: Optimal control of PDEs with regularized pointwise state constraints. Comput. Optim. Appl. 33, 187–208 (2006)
Tröltzsch, F., Prüfert, U., Weiser, M.: The convergence of an interior point method for an elliptic control problem with mixed control-state constraints. Comput. Optim. Appl. 39, 183–218 (2008)
Vierling, M.: Ein semiglattes Newton Verfahren für semidiskretisierte steuerungsbeschränkte Optimalsteuerungsprobleme. Diploma Thesis, Department Mathematik, Universität Hamburg (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hinze, M., Meyer, C. Variational discretization of Lavrentiev-regularized state constrained elliptic optimal control problems. Comput Optim Appl 46, 487–510 (2010). https://doi.org/10.1007/s10589-008-9198-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-008-9198-1