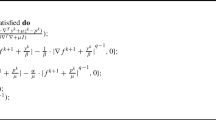Abstract
Based on the classic augmented Lagrangian multiplier method, we propose, analyze and test an algorithm for solving a class of equality-constrained non-smooth optimization problems (chiefly but not necessarily convex programs) with a particular structure. The algorithm effectively combines an alternating direction technique with a nonmonotone line search to minimize the augmented Lagrangian function at each iteration. We establish convergence for this algorithm, and apply it to solving problems in image reconstruction with total variation regularization. We present numerical results showing that the resulting solver, called TVAL3, is competitive with, and often outperforms, other state-of-the-art solvers in the field.







Similar content being viewed by others
References
Barzilai, J., Borwein, J.M.: Two-point step size gradient methods. IMA J. Numer. Anal. 8, 141–148 (1988)
Becker, S., Bobin, J., Candès, E.: NESTA: a fast and accurate first-order method for sparse recovery. SIAM J. Imaging Sci. 4, 1–39 (2011)
Bioucas-Dias, J., Figueiredo, M.: A new TwIST: two-step iterative thresholding algorithm for image restoration. IEEE Trans. Image Process. 16(12), 2992–3004 (2007)
Bioucas-Dias, J., Figueiredo, M.: Two-step algorithms for linear inverse problems with non-quadratic regularization. In: IEEE International Conference on Image Processing—ICIP 2007, San Antonio, TX, USA, September 2007
Boykov, Y., Veksler, O., Zabih, R.: Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 23(11), 1222–1239 (2001)
Candès, E., Romberg, J., Tao, T.: Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52(2), 489–509 (2006)
Candès, E., Tao, T.: Near optimal signal recovery from random projections: universal encoding strategies. IEEE Trans. Inf. Theory 52(12), 5406–5425 (2006)
Chambolle, A.: An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 20, 89–97 (2004)
Chan, T., Wong, C.K.: Total variation blind deconvolution. IEEE Trans. Image Process. 7(3), 370–375 (1998)
Chang, T., He, L., Fang, T.: MR image reconstruction from sparse radial samples using Bregman iteration. In: ISMRM (2006)
Donoho, D.: Compressed sensing. IEEE Trans. Inf. Theory 52(4), 1289–1306 (2006)
Donoho, D.: Neighborly polytopes and sparse solution of underdetermined linear equations. IEEE Trans. Inf. Theory (2006)
Duarte, M.F., Sarvotham, S., Baron, D., Wakin, M.B., Baraniuk, R.G.: Distributed compressed sensing of jointly sparse signals. In: 39th Asilomar Conference on Signals, Systems and Computers, pp. 1537–1541 (2005)
Fortin, M., Glowinski, R.: Méthodes de Lagrangien Augmenté. Application à la Résolution Numérique de Problèmes aux Limites. Dunod-Bordas, Paris (1982) (in French)
Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximations. Comput. Appl. Math. 2, 17–40 (1976)
Glowinski, R.: Numerical Methods for Nonlinear Variational Problems. Springer, Berlin (1984)
Glowinski, R., Marrocco, A.: Sur l’approximation par éléments finis d’ordre un et la résolution par pénalisation-dualité d’une classe de problèmes de Dirichlet nonlinéaires. C. R. Math. Acad. Sci. Paris 278A, 1649–1652 (1974) (in French)
Goldstein, T., Osher, S.: The split Bregman method for L1 regularized problems. SIAM J. Imaging Sci. 2(2), 323–343 (2009)
Grippo, L., Lampariello, F., Lucidi, S.: A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 23, 707–716 (1986)
Hager, W.W., Phan, D.T., Zhang, H.: Gradient-based methods for sparse recovery. SIAM J. Imaging Sci. 4, 146–165 (2011)
Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)
Jiang, H., Li, C., Haimi-Cohen, R., Wilford, P., Zhang, Y.: Scalable video coding using compressive sensing. Bell Labs Tech. J. 16, 149–169 (2012)
Laska, J., Kirolos, S., Duarte, M., Ragheb, T., Baraniuk, R., Massoud, Y.: Theory and implementation of an analog-to-information converter using random demodulation. In: Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, Louisiana (2007)
Li, C., Jiang, H., Wilford, P., Zhang, Y.: Video coding using compressive sensing for wireless communications. In: IEEE Wireless Communications and Networking Conference (WCNC), pp. 2077–2082 (2011). doi:10.1109/WCNC.2011.5779474
Li, C., Sun, T., Kelly, K., Zhang, Y.: A compressive sensing and unmixing scheme for hyperspectral data processing. IEEE Trans. Image Process. 21, 1200–1210 (2012)
Li, C., Zhang, Y., Yin, W.: http://www.caam.rice.edu/~optimization/L1/TVAL3/
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)
Natarajan, B.K.: Sparse approximate solutions to linear systems. SIAM J. Comput. 24, 227–234 (1995)
Nesterov, Yu.: Smooth minimization of non-smooth functions. Math. Program., Ser. A 103, 127–152 (2005)
Osher, S., Burger, M., Goldfarb, D., Xu, J., Yin, W.: An iterated regularization method for total variation based image restoration. Multiscale Model. Simul. 4, 460–489 (2005)
Powell, M.J.D.: A method for nonlinear constraints in minimization problems. In: Fletcher, R. (ed.) Optimization, pp. 283–298. Academic Press, London (1969)
Rockafellar, R.T.: The multiplier method of Hestenes and Powell applied to convex programming. J. Optim. Theory Appl. 12(6), 555–562 (1973)
Rudin, L., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 259–268 (1992)
Sun, T., Woods, G.L., Duarte, M.F., Kelly, K.F., Li, C., Zhang, Y.: OBIC measurements without lasers or raster-scanning based on compressive sensing. In: Proceedings of the 35th International Symposium for Testing and Failure Analysis (2009)
Takhar, D., Laska, J.N., Wakin, M.B., Duarte, M.F., Baron, D., Sarvotham, S., Kelly, K.F., Baraniuk, R.G.: A new compressive imaging camera architecture using optical-domain compression. In: Computational Imaging IV, vol. 6065, pp. 43–52 (2006)
Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 1(4), 248–272 (2008)
Yang, J., Yin, W., Zhang, Y.: A fast alternating direction method for TVL1-L2 signal reconstruction from partial Fourier data. Technical Report, TR08-27, CAAM, Rice University (2008)
Yin, W., Osher, S., Goldfarb, D., Darbon, J.: Bregman iterative algorithms for ℓ 1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 1, 143–168 (2008)
Yin, W., Morgan, S., Yang, J., Zhang, Y.: Practical compressive sensing with Toeplitz and circulant matrices. In: Proceedings of Visual Communications and Image Processing (VCIP) (2010)
Zhang, H., Hager, W.W.: A nonmonotone line search technique and its application to unconstrained optimization. SIAM J. Optim. 14, 1043–1056 (2004)
Xiao, Y., Song, H.: An inexact alternating directions algorithm for constrained total variation regularized compressive sensing problems. J. Math. Imaging Vis. 44, 114–127 (2012)
Acknowledgements
The work of the first author was supported in part by NSF Grant DMS-0811188. The work of the second author was supported in part by NSF grants DMS-07-48839 and ECCS-1028790, as well as ONR Grant N00014-08-1-1101. The work of the fourth author was supported in part by NSF Grant DMS-0811188, ONR Grant N00014-08-1-1101, and NSF Grant DMS-1115950. The first and the fourth authors also appreciate a gift fund from Bell Labs, Alcatel-Lucent to Rice University that partially supported their travels to international conferences. Last but not least, we thank the two anonymous referees for their constructive criticism and their helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proof of Theorem 1
Appendix: Proof of Theorem 1
For notational simplicity, let us define
The proof of the theorem relies on two lemmas. The two lemmas are modifications of their counterparts in [40]. Since our objective may contain a non-differentiable part, the key modification is to connect this non-differentiable part to the differentiable part by means of alternating minimization. Otherwise, the line of proofs follows closely that given in [40].
The first lemma presents some basic properties and established that the algorithm is well-defined.
Lemma 1
If ∇ϕ k (x k )T d k ≤0 holds for each k, then for the sequences generated by Algorithm-NADA, we have ϕ k (x k )≤ϕ k−1(x k )≤C k for each k and {C k } is monotonically non-increasing. Moreover, if ∇ϕ k (x k )T d k <0, a step length α k >0 always exists so that the nonmonotone Armijo condition (11) holds.
Proof
Define real-valued function
then
Due to the nonmonotone Armijo condition (11) and ∇ϕ k (x k )T d k ≤0, we have
Therefore, \(D_{k}'(t) \ge0\) holds for any t≥0, and then D k is non-decreasing.
Since
we have
As is defined in Algorithm-NADA,
Therefore,
Hence, ϕ k (x k )≤ϕ k−1(x k )≤C k holds for any k.
Furthermore,
i.e.,
that is,
Thus, {C k } is monotonically non-increasing.
If C k is replaced by ϕ k (x k ) in (11), the nonmonotone Armijo condition becomes the standard Armijo condition. It is well-known that α k >0 exists for the standard Armijo condition while ∇ϕ k (x k )T d k <0 and ϕ is bounded below. Since ϕ k (x k )≤C k , it follows α k >0 exists as well for the nonmonotone Armijo condition:
Now we defining the quantity A k by
By induction, it is easy to show that C k is bounded above by A k . Together with the facts that C k is also bounded below by ϕ k (x k ) and α k >0 always exists, it is clear that Algorithm-NADA is well-defined. □
In the next lemma, a lower bound for the step length generated by Algorithm-NADA will be given.
Lemma 2
Assume that ∇ϕ k (x k )T d k ≤0 for all k and that Lipschitz condition (19) holds with constant L. Then
The proof is omitted here since the proof of Lemma 2.1 in [40] is directly applicable.
With the aid of the lower bound (24), we now are ready to prove Theorem 1. We need to establish the two relationships given in (20).
Proof
First, by definition in Algorithm-NADA,
Hence, it always holds true that
Now it suffices to show that the limit holds true in (20). Consider the nonmonotone Armijo condition:
If ρα k <α max, in view of the lower bound (24) on α k in Lemma 2 and the direction assumption (18),
On the other hand, if ρα k ≥α max, the lower bound (24), together with the direction assumption (18), gives
Introducing a constant
we can combine the above inequalities into
Next we show by induction that for all k
which obviously holds for k=0 given that Q 0=1. Assume that (27) holds for k=j. Then
implying that (27) also holds for k=j+1. Hence, (27) holds for all k.
It follows from (26) and (27) that
Since ϕ is bounded below by assumption, {C k } is also bounded below. In addition, by Lemma 1, {C k } is monotonically non-increasing, hence convergent. Therefore, the left-hand side of (28) tends to zero, so does the right-hand side; i.e., ∥∇ϕ k (x k )∥→0. Finally, by definition (22),
which completes the proof. □
Rights and permissions
About this article
Cite this article
Li, C., Yin, W., Jiang, H. et al. An efficient augmented Lagrangian method with applications to total variation minimization. Comput Optim Appl 56, 507–530 (2013). https://doi.org/10.1007/s10589-013-9576-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-013-9576-1