Adaptively refined dynamic program for linear spline regression

Abstract

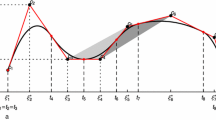
The linear spline regression problem is to determine a piecewise linear function for estimating a set of given points while minimizing a given measure of misfit or error. This is a classical problem in computational statistics and operations research; dynamic programming was proposed as a solution technique more than 40 years ago by Bellman and Roth (J Am Stat Assoc 64:1079–1084, 1969). The algorithm requires a discretization of the solution space to define a grid of candidate breakpoints. This paper proposes an adaptive refinement scheme for the grid of candidate breakpoints in order to allow the dynamic programming method to scale for larger instances of the problem. We evaluate the quality of solutions found on small instances compared with optimal solutions determined by a novel integer programming formulation of the problem. We also consider a generalization of the linear spline regression problem to fit multiple curves that share breakpoint horizontal coordinates, and we extend our method to solve the generalized problem. Computational experiments verify that our nonuniform grid construction schemes are useful for computing high-quality solutions for both the single-curve and two-curve linear spline regression problem.

Appendix

1.1 Proof of Proposition 2

The DP requires the evaluation of $F_{\widehat{m}}(i,j)$ for $\widehat{m}=1,\ldots , m$, $i=1,\ldots ,p$, and $j\in S(t_i)$.

First, $F_1(i,j)$ is evaluated for $i=2,\ldots ,p-m+1$ and and each such evaluation is $O(1)$ (assuming that $E$ is given). For each $i\in \{1,\ldots ,p-(m-1)\}$, $|S^w(t_i)|\le q$ for each $w\in W$. Then $q^{2v}$ operations are used to enumerate elements of $S^w(t_1)\times S^w(t_i)$ in order to determine , for . Hence, in total at most $(p-m)q^{2v}$ evaluations are required to determine $F_1(i,j)$ for $i=2,\ldots ,p-m+1$ and .

Next, for $\widehat{m}\in \{ 2,\ldots ,m\}$, $F_{\widehat{m}}(i,j)$ is evaluated for $i\in I \mathop {=}\limits ^{\text {Def}} \{\widehat{m}+1,\ldots ,p-m+\widehat{m}\}$ and . Note that $\left| I\right| = p-m$. For a given $i\in I$ and $j\in S(t_{i})$, $F_{\widehat{m}}(i,j)$ evaluates $F_{\widehat{m}-1}(k,\cdot )$ for $k\in \{\widehat{m}+1,\ldots , i-1\}$. For each pair $(k,i)\in I\times I$ with $k\ne i$, and $w\in W$, at most $q^2$ evaluations are required. Then, the number of segment combinations over $w\in W$ is $q^{2\left| W\right| }=q^{2v}$. There are at most ${(p-m)\atopwithdelims ()2}$ such pairs (where $k\ne i$), so that at most $\frac{(p-m)(p-m-1)}{2}q^{2v}$ evaluations are required to compute $F_{\widehat{m}}(i,j)$ for $i=\widehat{m},\ldots ,p-m+\widehat{m}$ and .

Hence, the number of operations is bounded by

$$\begin{aligned}&(p-m)q^{2v}+(m-1)\frac{(p-m)(p-m-1)}{2}q^{2v}\\&\quad =(p-m)q^2\left( \frac{(m+1){+}(m-1)(p-m)}{2}\right) {\in } O((p-m)^2q^{2v}m)\subseteq O(p^2q^{2v}m). \end{aligned}$$

$\square$