Skip to main content
SpringerLink
Log in

A non-overlapping DDM combined with the characteristic method for optimal control problems governed by convection–diffusion equations

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

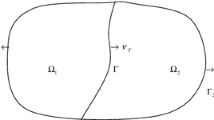
In this paper, we consider a non-overlapping domain decomposition method combined with the characteristic method for solving optimal control problems governed by linear convection–diffusion equations. The whole domain is divided into non-overlapping subdomains, and the global optimal control problem is decomposed into the local problems in these subdomains. The integral mean method is utilized for the diffusion term to present an explicit flux calculation on the inter-domain boundary in order to communicate the local problems on the interfaces between subdomains. The convection term is discretized along the characteristic direction. We establish the fully parallel and discrete schemes for solving these local problems. A priori error estimates in \(L^2\)-norm are derived for the state, co-state and control variables. Finally, we present numerical experiments to show the validity of the schemes and verify the derived theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Peaceman, D.W.: Fundamentals of Numerical Reservoir Simulation. Elsevier, Amsterdam (1977)

    Google Scholar 

  2. Grossmann, C., Roos, H.G., Stynes, M.: Numerical Treatment of Partial Differential Equations. Springer, Berlin (2007)

    Book  MATH  Google Scholar 

  3. Lions, J.L.: Optimal Control of Systems Governed by Partial Differential Equations. Springer, Berlin (1971)

    Book  MATH  Google Scholar 

  4. Neittaanmäki, P., Tiba, D.: Optimal Control of Nonlinear Parabolic Systems, Theroy, Algorithms and Applications. Marcel Dekker, INC., New York (1994)

    MATH  Google Scholar 

  5. Liu, W.B., Yan, N.N.: Adaptive Finite Element Method for Optimal Control Governed by PDEs. Science Press, Beijing (2008)

    Google Scholar 

  6. Ge, L., Liu, W.B., Yang, D.P.: Adaptive finite element approximation for a constrained optimal control problem via multi-meshes. J. Sci. Comput. 41(2), 238–255 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Yan, N.N., Zhou, Z.J.: A prior and a posteriori error analysis of edge stabilization Galerkin method for the optimal control problem governed by convection-dominated diffusion equation. J. Comput. Appl. Math. 223(1), 198–217 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bartlett, R.A., Heinkenschloss, M., Ridzal, D., Waanders, B.V.B.: Domain decomposition methods for advection dominated linear-quadratic elliptic optimal control problems. Comput. Methods Appl. Mech. Eng. 195, 6428–6447 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  9. Becker, R., Vexler, B.: Optimal control of the convection–diffusion equation using stabilized finite element methods. Numer. Math. 106(3), 349–367 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Heinkenschloss, M., Leykekhman, D.: Local error estimates for SUPG solutions of advection-dominated elliptic linear-quadratic optimal control problems. SIAM J. Numer. Anal. 47(6), 4607–4638 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhu, J., Zeng, Q.: A mathematical theoretical frame for control of air pollution. Sci. China Ser. D 32, 864–870 (2002)

    Google Scholar 

  12. Bensoussan, A., Glowinski, R., Lions, J.L.: Mééthode de décomposition appliquée au contrôle optimal de systèmes distribués. In: 5th IFIP Conference on Optimization Techniques, Lecture Notes in Computer Science, p. 5. Springer, Berlin (1973)

  13. Lagnese, J.E., Leugering, G.: Domain Decomposition Methods in Optimal Control of Partial Differential Equations. Volume 148 of International Series of Numerical Mathematics, p. 148. Birkhäuser, Basel (2004)

    Book  Google Scholar 

  14. Benamou, J.D.: Domain decomposition methods with coupled transmission conditions for the optimal control of systems governed by elliptic partial differential equations. SIAM J. Numer. Anal. 33(6), 2401–2416 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  15. Heinkenschloss, M., Nguyen, H.: Neumann–Neumann domain decomposition preconditioners for linear-quadratic elliptic optimal control problems. SIAM J. Sci. Comput. 28(3), 1001–1028 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  16. Heinkenschloss, M., Herty, M.: A spatial domain decomposition method for parabolic optimal control problems. J. Comput. Appl. Math. 201, 88–111 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  17. Hou, L.S., Lee, J.: A Robin–Robin non-overlapping domain decomposition method for an elliptic boundary control problem. Int. J. Numer. Anal. Model. 8(3), 443–465 (2011)

    MathSciNet  MATH  Google Scholar 

  18. Benamou, J.D.: Domain decomposition, optimal control of system governed by partial differential equations, and sysnthesis of feedback laws. J. Optim. Theory App. 102(1), 15–36 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ewing, R.E., Russell, T.F., Wheeler, M.F.: Convergence analysis of an approximation of miscible displacement in porous media by mixed finite elements and a modified method of characteristics. Comput. Methods Appl. Mech. Eng. 47, 73–92 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  20. Russell, T.F.: Time stepping along characteristics with incomplete iteration for a Galerkin approximation of miscible displacement in porous media. SIAM J. Numer. Anal 22, 970–1013 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  21. Yuan, Y.R., Chang, L., Li, C.F., Sun, T.J.: Domain decomposition modified with characteristic finite element method for numerical simulation of semiconductor transient problem of heat conduction. J. Math. Res. 7(3), 61–74 (2015)

    Article  MathSciNet  Google Scholar 

  22. Huang, C.S.: The modified method of characteristics with adjusted advection and an accelerated domain decomposition procedure. Ph.D. thesis, Purdue University, ProQuest LLC, Ann Arbor, MI (1998)

  23. Ma, K.Y., Sun, T.J., Yang, D.P.: Parallel Galerkin domain decomposition procedures for parabolic equation on general domain. Numer. Methods Partial Differ. Equ. 25(5), 1167–1194 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Ma, K.Y., Sun, T.J.: Galerkin domain decomposition procedures for parabolic equations on rectangular domain. Int. J. Numer. Methods Fluids 62(4), 449–472 (2010)

    MathSciNet  MATH  Google Scholar 

  25. Sun, T.J., Ma, K.Y.: Dynamic parallel Galerkin domain decomposition procedures with grid modification for parabolic equation. Int. J. Numer. Methods Fluids 66(12), 1506–1529 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Sun, T.J., Ma, K.Y.: Domain decomposition procedures combined with \(H^1\)-Galerkin mixed finite element method for parabolic equation. J. Comput. Appl. Math. 267, 33–48 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  27. Dawson, C.N., Dupont, T.F.: Explicit/Implicit conservative Galerkin domain decomposition procedures for parabolic problems. Math. Comput. 58, 21–35 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  28. Sun, T.J., Ma, K.Y.: Parallel Galerkin domain decomposition procedures for wave euqation. J. Comput. Appl. Math. 233, 1850–1865 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ma, K.Y., Sun, T.J.: Parallel Galerkin domain decomposition procedures based on the streamline diffusion method for convection-diffusion problems. J. Comput. Appl. Math. 235(15), 4464–4479 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  30. Adams, R.: Sobolev Spaces. Academic, New York (1975)

    MATH  Google Scholar 

  31. Lefschetz, S.: Differential Equations: Geometric Theory. Dover, New York (1979)

    MATH  Google Scholar 

  32. Fu, H.F., Rui, H.X.: A priori error estimates for optimal control problems governed by transient advection–diffusion equations. J. Sci. Comput. 38, 290–315 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  33. Houston, P.: Adaptive Lagrange–Galerkin methods for unsteady convection–diffusion problems. Math. Comput. 70, 77–106 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  34. Süli, E.: Convergence and nonlinear stability of the Lagrange–Galerkin method for the Navier–Stokes equation. Numer. Math. 53, 459–483 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  35. Douglas, J., Russell, T.F.: Numerical methods for convection-dominated diffusion problems based on combining the method of with finite element or finite difference procedures. SIAM J. Numer. Anal. 19, 871–885 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhu, J.L., Yuan, Z.Q.: Boundary Element Analysis. Science Press, Beijing (2009). (in Chinese)

    Google Scholar 

  37. Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Method. Volume 15 of Texts in Applied Mathematics. Springer, Berlin (1996)

    Google Scholar 

  38. Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland Publication, Amsterdam (1978)

    MATH  Google Scholar 

  39. Nitsche, J.: \(L^{\infty }\)-error analysis for finite elements. In: Whiteman, J.R. (ed.) The Mathematics of Finite Elements and Applications III, pp. 173–186. Academic Press, New York (1979)

    Google Scholar 

  40. Schatz, A.H., Wahlbin, L.B.: Maximun norm estimates in the finite element method on plane polygonal domains, I. Math. Comput. 32, 73–109 (1978)

    MATH  Google Scholar 

  41. Schatz, A.H., Wahlbin, L.B.: Maximun norm estimates in the finite element method on plane polygonal domains, II. Math. Comput. 33, 485–492 (1979)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, People’s Republic of China

    Tongjun Sun & Keying Ma

Authors
  1. Tongjun Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Keying Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Keying Ma.

Additional information

This work is supported by the NSF of China (Nos. 11301300, 11271231) and the NSF of Shandong Province, China (No. ZR2018MA007).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, T., Ma, K. A non-overlapping DDM combined with the characteristic method for optimal control problems governed by convection–diffusion equations. Comput Optim Appl 71, 273–306 (2018). https://doi.org/10.1007/s10589-018-0008-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-018-0008-0

Keywords

Search

Navigation