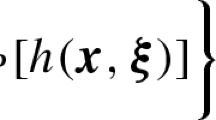Abstract
Decomposition methods have been well studied for solving two-stage and multi-stage stochastic programming problems, see Rockafellar and Wets (Math. Oper. Res. 16:119–147, 1991), Ruszczyński and Shapiro (Stochastic Programming, Handbook in OR & MS, North-Holland Publishing Company, Amsterdam, 2003) and Ruszczyński (Math. Program. 79:333–353, 1997). In this paper, we propose an algorithmic framework based on the fundamental ideas of the methods for solving two-stage minimax distributionally robust optimization (DRO) problems where the underlying random variables take a finite number of distinct values. This is achieved by introducing nonanticipativity constraints for the first stage decision variables, rearranging the minimax problem through Lagrange decomposition and applying the well-known primal-dual hybrid gradient (PDHG) method to the new minimax problem. The algorithmic framework does not depend on specific structure of the ambiguity set. To extend the algorithm to the case that the underlying random variables are continuously distributed, we propose a discretization scheme and quantify the error arising from the discretization in terms of the optimal value and the optimal solutions when the ambiguity set is constructed through generalized prior moment conditions, the Kantorovich ball and \(\phi\)-divergence centred at an empirical probability distribution. Some preliminary numerical tests show the proposed decomposition algorithm featured with parallel computing performs well.


Similar content being viewed by others
Notes
In some literature, total variation metric is defined as \(\mathsf {dl}_{TV}=\sup _{B\in \mathscr {B}}|P(B) - Q(B)|\), see [9].
References
Athreya, K.B., Lahiri, S.N.: Measure Theory and Probability Theory. Springer, New York (2006)
Bertsimas, D., Doan, X.V., Natarajan, K., Teo, C.P.: Models for minimax stochastic linear optimization problems with risk aversion. Math. Oper. Res. 35, 580–602 (2010)
Bertsimas, D., Parys, B. V.: Bootstrap robust prescriptive analytics. arXiv:1711.09974 (2017)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging. Vis. 40, 120–145 (2011)
Delage, E., Ye, Y.: Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 58, 592–612 (2010)
Esser, E., Zhang, X., Chan, T.: A general framework for a class of first order primal-dual algorithms for Convex Optimization in Imaging Science. SIAM J. Imaging Sci. 3, 1015–1046 (2010)
Fan, K.: Minimax theorems. Izv. Nats. Akad. Nauk Armen. Mekh 39, 42–47 (1953)
Gao, R., Kleywegt, A.: Distributionally robust stochastic optimization with Wasserstein distance. arXiv:1604.02199 (2016)
Gibbs, A.L., Su, F.E.: On choosing and bounding probability metrics. Int. Stat. Rev. 70, 419–435 (2002)
Goh, J., Sim, M.: Distributionally robust optimization and its tractable approximations. Oper. Res. 58, 902–917 (2010)
Goldstein, T., Li, M., Yuan, X., Esser, E., Baraniuk, R.: Adaptive primal-dual hybrid gradient methods for saddle-point problems. arXiv:1305.0546 (2013)
Guo, S., Xu, H., Zhang, L.: Convergence analysis for mathematical programs with distributionally robust chance constraint. SIAM J. Optim. 27, 784–816 (2017)
Guo, S., Xu, H.: Distributionally robust shortfall risk optimization model and its approximation. Math. Program. 174, 473–498 (2019)
Hanasusanto, G.A., Kuhn, D.: Conic programming reformulations of two-stage distributionally robust linear programs over Wasserstein balls. Oper. Res. 66, 849–869 (2018)
He, B., Ma, F., Yuan, X.: An algorithm framework of generalized primal-dual hybrid gradient methods for saddle point problems. J. Math. Imaging. Vis. 58, 279–293 (2017)
He, B., Yuan, X.: Convergence analysis of primal-dual algorithms for a saddle-point problem: from contraction perspective. SIAM J. Imaging Sci. 5, 119–149 (2012)
Jiang, R., Guan, Y.: Risk-averse two-stage stochastic program with distributional ambiguity. Oper. Res. 66, 1390–1405 (2018)
Liu, Y., Pichler, A., Xu, H.: Discrete approximation and quantification in distributionally robust optimization. Math. Oper. Res. 44, 19–37 (2019)
Liu, Y., Yuan, X., Zeng, S., Zhang, J.: Primal-dual hybrid gradient method for distributionally robust optimization problems. Oper. Res. Lett. 45, 625–630 (2017)
Liu, Y., Yuan, X., Zhang, J.: Quantitative stability analysis of stochastic programs with distributionally robust second order dominance constraints, manuscript (2017)
Love, D., Bayrakcan, G.: Phi-divergence constrained ambiguous stochastic programs for data-driven optimization, available on researchgate.net (2016)
Mohajerin Esfahani, P., Kuhn, D.: Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Math. Program. 171, 115–166 (2018)
Pardo, L.: Statistical Inference Based on Divergence Measures. Chapman and Hall/CRC, Boca Raton (2005)
Pflug, G.C., Pichler, A.: Approximations for probability distributions and stochastic optimization problems. In: Bertocchi, M., Consigli, G., Dempster, M.A.H. (eds.) Stochastic Optimization Methods in Finance and Energy, vol. 163 of International Series in Operations Research & Management Science. Springer, New York (2011)
Pflug, G.C., Pichler, A.: Multistage Stochastic Optimization. Springer Series in Operations Research and Financial Engineering. Springer, New York (2014)
Pflug, G.C., Wozabal, D.: Ambiguity in portfolio selection. Quant. Financ. 7, 435–442 (2007)
Pichler, A., Xu, H.: Quantitative stability analysis for minimax distributionally robust risk optimization, To appear in Math. Program. (2018)
Rachev, S.T.: Probability Metrics and the Stability of Stochastic Models. Wiley, West Sussex (1991)
Rockafellar, R., Wets, R.J.-B.: Scenarios and policy aggregation in optimization under uncertainty. Math. Oper. Res. 16, 119–147 (1991)
Rockafellar, R., Sun, J.: Solving monotone stochastic variational inequalities and complementarity problems by progressive hedging. Math. Program. 174, 453–471 (2019)
Römisch, W.: Stability of stochastic programming problems. In: Rusczyński, A., Shapiro, A. (eds.) Stochastic Programming. Handbook in OR & MS, vol. 10. North-Holland Publishing Company, Amsterdam (2003)
Ruszczyński, A.: Decomposition method. In: Rusczyński, A., Shapiro, A. (eds.) Stochastic Programming, Handbook in OR & MS, vol. 10. North-Holland Publishing Company, Amsterdam (2003)
Ruszczyński, A.: Decomposition methods in stochastic programming. Math. Program. 79, 333–353 (1997)
Rahimian, H., Bayraksan, G., Homem-de-Mello, T.: Identifying effective scenarios in distributionally robust stochastic programs with total variation distance. Math. Program. 173, 393–430 (2019)
Rusczyński, A., Shapiro, A.: Stochastic Programming, Handbook in OR & MS, vol. 10. North-Holland Publishing Company, Amsterdam (2003)
Scarf, H.: A min–max solution of an inventory problem. In: Arrow, K.S., Karlin, S., Scarf, H.E. (eds.) Studies in the Mathematical Theory of Inventory and Production, pp. 201–209. Stanford University Press, Palo Alto (1958)
Shapiro, A., Ahmed, S.: On a class of minimax stochastic programs. SIAM J. Optim. 14, 1237–1249 (2004)
Shapiro, A.: On duality theory of conic linear problems. In: Goberna, M.A., López, M.A. (eds.) Semi-Infinite Programming. Nonconvex Optimization and Its Applications, vol. 57. Springer, Boston (2001)
Sun, J., Liao, L.Z., Rodrigues, B.: Quadratic two-stage stochastic optimization with coherent measures of risk. Math. Program. 168, 599–613 (2018)
Sun, H., Xu, H.: Convergence analysis for distributionally robust optimization and equilibrium problems. Math. Oper. Res. 41, 377–401 (2016)
Weiss, P., Blanc-Feraud, L., Aubert, G.: Efficient schemes for total variation minimization under constraints in image processing. SIAM J. Sci. Comput. 31, 2047–2080 (2009)
Wiesemann, W., Kuhn, D., Sim, M.: Distributionally robust convex optimization. Oper. Res. 62, 1358–376 (2014)
Xu, H., Liu, Y., Sun, H.: Distributionally robust optimization with matrix moment constraints: Lagrange duality and cutting plane methods. Math. Program. 169, 489–529 (2018)
Zhang, Y., Jiang, R., Shen, S.: Ambiguous chance-constrained binary programs under mean-covariance information. SIAM J. Optim. 28, 2922–2944 (2018)
Zhang, X., Burger, M., Osher, S.: A unified primal-dual algorithm framework based on Bregman iteration. J. Sci. Comput. 46, 20–46 (2010)
Zhao, C., Guan, Y.: Data-driven risk-averse two-stage stochastic program with ζ-structure probability metrics, available at Optimization Online (2015). http://www.optimization-online.org/DB_FILE/2015/07/5014.pdf
Zolotarev, V.M.: Probability metrics. Teoriya Veroyatnostei IEE Primeneniya 28, 264–287 (1983)
Zhang, Z., Ahmend, S., Lan, G.: Efficient algorithms for distributionally robust stochastic optimization with discrete scenario support. arXiv:1909.11216 (2019)
Zhu, M., Chan, T. F.: An efficient primal dual hybrid gradient algorithm for total variation image restoration. CAM Report 08-34, UCLA, Los Angeles, CA (2008)
Acknowledgements
We would like to thank Shabbir Ahmed for initiating the research in a private discussion with the 3rd author during the 14th international conference on stochastic programming in Búzios and his further encouragement during the preparation of the paper. We would also like to thank the two anonymous referees for insightful comments which help us significantly strengthen the presentation of the paper.
Funding
The funding was provided by National Natural Science Foundation of China (Grant No. 11871276 and 11771405).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 1
The inequality holds trivially if \(Q\in {\tilde{{{\mathcal {P}}}}}\). So we only consider the case when \(Q\not \in {\tilde{{{\mathcal {P}}}}}\). We proceed the proof in three steps.
Step 1. By the definition of the total variation norm (see [1]), \(||P||= \sup _{\Vert \phi \Vert ^*\le 1} \langle P, \phi \rangle ,\) where \(\Vert \cdot \Vert ^*\) is the dual of norm \(\Vert \cdot \Vert\). Moreover, by the definition of the total variation metric
where \(\text{ cl }(\cdot )\) denotes closure of a set under topology of weak convergence, \(\langle P, \phi \rangle :=\int _{\tilde{\varXi }}\phi (\xi )P(d\xi )\) and the exchange is justified by [7, Theorem 2] under our assumption that \(\tilde{{{\mathcal {P}}}}\) is weakly compact. Note that we write \(\langle P, \phi \rangle\) for \({\mathbb {E}}_P[\phi ]\) in that later on we will relax P from a probability measure to a positive measure, and we will be able to see P clearly as a variable in the moment system and the moment system is linear in P. It is easy to observe that \(\mathsf {dl}_{TV}(P,{{\mathcal {P}}})\le 2\). Moreover, under the Slater type condition (16), it follows by [38, Proposition 3.4] that
where \(\mathscr {M}_+(\tilde{\varXi })\) denotes the set of all positive measures defined on \(\tilde{\varXi }\), \(\varLambda :=\{(\lambda _1,\cdots ,\lambda _q): \lambda _i\succeq 0, \; \text{ for }\; i=p+1,\ldots ,q\},\) and \(A \bullet B\) denotes the Frobenius product of the two matrices A and B. If there exists some \(\xi _i\) such that \(\phi (\xi _i) -\lambda \bullet \varPsi (\xi _i) -\lambda _0>0\), then the value of (49) is \(-\infty\) because we can choose \(P=\alpha \delta _{\xi _i}(\cdot )\), where \(\delta _{\xi _i}(\cdot )\) denotes the Dirac probability measure at \(\xi _i\), and drive \(\alpha\) to \(+\infty\). Thus we are left to consider that case with
Consequently we can rewrite (49) as
The second inequality is due to the fact that the optimum is attained at \(P=0\). Summarizing the discussions above, we arrive at
The first equality is obtained by swapping the two “sup” operations because their optimal values are bounded. To see how the second equality holds, we may compare the optimal value of the second and third programs above. Let’s denote the second one by (P) and the third one by (P’). Observe that (P’) is transferred from (P) by replacing \(\phi (\xi )\) in the objective by the largest possible value \(\min \{\lambda \bullet \varPsi (\xi )+\lambda _0, 1\}\) and in the constraint the smallest possible value \(-1\) making the feasible set largest. This means the optimal value of (P) is less or equal to that of (P’). On the other hand, for any optimal solution \((\lambda ^*, \lambda _0^*)\) of (P’), let \(\phi ^*:=\min \{\lambda ^*\bullet \varPsi (\xi )+\lambda _0^*, 1\}\). Then \((\lambda ^*, \lambda _0^*, \phi ^*)\) is a feasible solution of (P) which implies in turn the optimal value of (P’) is less or equal to that of (P). Note also that the optimal value is \(\mathsf {dl}_{TV}(Q,{\tilde{{{\mathcal {P}}}}})\in [0,2]\).
Step 2. We show that the optimization problem at the right hand side of (50) has a bounded optimal solution. Let
denote the feasible set of (50) and
Then
To see this, let \((\lambda , \lambda _0)\in {{\mathcal {F}}}\) and \(t=\Vert \lambda \Vert +|\lambda _0+1|\). If \(t=0\), then \((0_q,-1)\in \{(0_q,-1)+t{{\mathcal {C}}}: t\in [0,+\infty )\}\). Consider the case that \(t\ne 0\). Then it is easy to verify that \((\lambda , \lambda _0+1)/t\in {{\mathcal {C}}}\) and hence \((\lambda , \lambda _0)\in (0_q,-1)+t{{\mathcal {C}}}\). This shows \({{\mathcal {F}}}\subset \{(0_q,-1)+t{{\mathcal {C}}}: t\in [0,+\infty )\}\). The converse inclusion is obvious.
Note that \({{\mathcal {C}}}\ne \emptyset\). Otherwise we would have
which implies \(P\in \tilde{{{\mathcal {P}}}}\), a contradiction. In what follows, we consider the case when \({{\mathcal {C}}}\ne \emptyset\). From (51) we immediately have
On the other hand, by Assumption 1 and (17),
and there exists a closed neighborhood of \((0,0_{q})\) with radius \(\epsilon _0\), denoted by \(\epsilon _0{{\mathcal {B}}}\), such that
Let \(({\tilde{\lambda }}, {\tilde{\lambda }}_0)\in {{\mathcal {C}}}\). Then there exists \(\tilde{w}\in \epsilon _0{{\mathcal {B}}}\) (depending on \(({\tilde{\lambda }}, {\tilde{\lambda }}_0)\)) such that \(\langle {\tilde{w}}, (\tilde{\lambda },{\tilde{\lambda }}_0)\rangle \le -\epsilon _0\). In other words, there exist \(\tilde{P}\in \mathscr {M}_+(\tilde{\varXi })\) and \(\eta \in {{\mathcal {K}}}_-^{q-p}\) such that
Since \(-\eta \bullet {\tilde{\lambda }}_I\ge 0\), we deduce from (52) and (53) that \(- \tilde{\lambda }_0- {\tilde{\lambda }} \bullet \mu \le -\epsilon _0.\) The inequality holds for every \(({\tilde{\lambda }}, {\tilde{\lambda }}_0)\in {{\mathcal {C}}}\). Note that for any \((\lambda ,\lambda _0)\in {{\mathcal {F}}}\), we may write it in the form
where \(({\hat{\lambda }},{\hat{\lambda }}_0) =(0_q, -1)\), \((\tilde{\lambda },\tilde{\lambda }_0)\in {{\mathcal {C}}}\) and \(t\ge 0\). Observe that \(\langle Q, \min \{\lambda \bullet \varPsi +\lambda _0, 1\}\rangle \in [-1,1]\) and
Note that the optimal value of the optimization problem at the right hand side of (50) is positive, which implies for any optimal solution \((\lambda ^*, \lambda _0^*) = (0_q, -1) + (\bar{\lambda }^*, \bar{\lambda }_0^*)\) with \((\bar{\lambda }^*, \bar{\lambda }_0^*)\in t^*{{\mathcal {C}}}\) we must have \(1-\mu \bullet 0_q -(-1) - t^* \epsilon _0 = 2-t^*\epsilon _0>0\) or equivalently \(t^*< \frac{2}{\epsilon _0}.\) Let \(t_1= \frac{2}{\epsilon _0}\) and \({{\mathcal {F}}}_1:={{\mathcal {F}}}_0 + \{t{{\mathcal {C}}}: t_1\ge t\ge 0\}\). Based on the discussions above, we conclude that the optimization problem at the right hand side of (50) has an optimal solution in \({{\mathcal {F}}}_1\).
Step 3. Let \(C_1:=\max _{(\lambda , \lambda _0)\in {{\mathcal {F}}}_1}\Vert \lambda \Vert\). Then
where \(C_1=\frac{2}{\epsilon _0}+1\). The inequality also holds for the case when \({{\mathcal {C}}}=\emptyset\) because \({{\mathcal {F}}}_0\subset {{\mathcal {F}}}_1\). Note that the above result holds for all \({\tilde{{{\mathcal {P}}}}}\) when \(\bar{\varXi }\subset {\tilde{\varXi }}\subset \varXi\), which include both continuous and discrete support set case, the proof is complete. \(\square\)
Rights and permissions
About this article
Cite this article
Chen, Y., Sun, H. & Xu, H. Decomposition and discrete approximation methods for solving two-stage distributionally robust optimization problems. Comput Optim Appl 78, 205–238 (2021). https://doi.org/10.1007/s10589-020-00234-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-020-00234-7