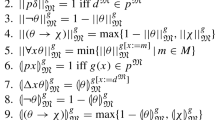Skip to main content
SpringerLink
Log in

Relatively quantified constraint satisfaction

  • Published:
Constraints Aims and scope Submit manuscript

Abstract

The constraint satisfaction problem (CSP) is a convenient framework for modelling search problems; the CSP involves deciding, given a set of constraints on variables, whether or not there is an assignment to the variables satisfying all of the constraints. This paper is concerned with the more general framework of quantified constraint satisfaction, in which variables can be quantified both universally and existentially. We study the relatively quantified constraint satisfaction problem (RQCSP), in which the values for each individual variable can be arbitrarily restricted. We give a complete complexity classification of the cases of the RQCSP where the types of constraints that may appear are specified by a constraint language.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Böhler, E., Creignou, N., Reith, S., & Vollmer, H. (2004). Playing with boolean blocks, part II: Constraint satisfaction problems. ACM SIGACT-Newsletter, 35(1), 22–35.

    Article  Google Scholar 

  2. Börner, F., Bulatov, A., Krokhin, A., & Jeavons, P. (2003). Quantified constraints: Algorithms and complexity. In Computer Science Logic 2003.

  3. Bulatov, A. (2003). Tractable conservative constraint satisfaction problems. In Proceedings of 18th IEEE symposium on logic in computer science (LICS ’03) pp. 321–330. Extended version appears as Oxford University technical report PRG-RR–03-01.

  4. Bulatov, A. A. (2006). A dichotomy theorem for constraint satisfaction problems on a 3-element set. Journal of the ACM (JACM), 53, 66–120.

    Article  MathSciNet  Google Scholar 

  5. Bulatov, A., & Dalmau, V. (2006). A simple algorithm for mal’tsev constraints. SIAM Journal of Computing, 36(1), 16–27.

    Article  MATH  MathSciNet  Google Scholar 

  6. Bulatov, A., Chen, H., & Dalmau, V. (2004). Learnability of relatively quantified generalized formulas. In Proceedings of the 15th international conference on algorithmic learning theory (ALT).

  7. Bulatov, A., Krokhin, A., & Jeavons, P. (2000). Constraint satisfaction problems and finite algebras. In Proceedings 27th international colloquium on automata, languages, and programming – ICALP’00, Lecture Notes In Computer Science (Vol. 1853, pp. 272–282)

  8. Chen, H. (2004). The computational complexity of quantified constraint satisfaction. Technical Report Ph.D. thesis, Cornell University. http://www.tecn.upf.es/~hchen.

  9. Chen, H. (2005). Quantified constraint satisfaction, maximal constraint languages, and symmetric polymorphisms. In STACS.

  10. Chen, H. (2006). The complexity of quantified constraint satisfaction: Collapsibility, sink algebras, and the three-element case. arxiv cs.LO/0607106.

  11. Creignou, N., Khanna, S., & Sudan, M. (2001). Complexity classification of boolean constraint satisfaction problems. SIAM Monographs on Discrete Mathematics and Applications. Philadelphia: Society for Industrial and Applied Mathematics.

    Google Scholar 

  12. Dalmau, V. (1997). Some dichotomy theorems on constant-free quantified boolean formulas. Technical Report LSI-97-43-R, Llenguatges i Sistemes Informàtics - Universitat Politècnica de Catalunya.

  13. Dalmau, V., & Pearson, J. (1999). Closure functions and width 1 problems. In CP 1999, pp. 159–173.

  14. Feder, T., & Kolaitis, P. (2006). Closures and dichotomies for quantified constraints. Electronic Colloquium on Computational Complexity, Report TR06-160.

  15. Feder, T., & Vardi, M. Y. (1998). The computational structure of monotone monadic snp and constraint satisfaction: A study through datalog and group theory. SIAM Journal of Computation, 28(1), 57–104.

    Article  MATH  MathSciNet  Google Scholar 

  16. Jeavons, P. (1998). On the algebraic structure of combinatorial problems. Theoretical Computer Science, 200, 185–204.

    Article  MATH  MathSciNet  Google Scholar 

  17. Jeavons, P., Cohen, D., & Cooper, M. (1998). Constraints, consistency, and closure. Artificial Intelligence, 101(1–2), 251–265.

    Article  MATH  MathSciNet  Google Scholar 

  18. Jeavons, P. G., Cohen, D. A., & Gyssens, M. (1997). Closure properties of constraints. Journal of the ACM, 44, 527–548.

    Article  MATH  MathSciNet  Google Scholar 

  19. Krokhin, A., Bulatov, A., & Jeavons, P. (2005). The complexity of constraint satisfaction: An algebraic approach. Heidelberg: Springer.

    Google Scholar 

  20. Martin, B., & Madelaine, F. (2006). Towards a trichotomy for quantified H-coloring. In Logical approaches to computational barriers, second conference on computability in Europe, lecture notes in computer science. Springer.

  21. Pöschel, R., & Kaluz̆nin, L. A. (1979). Funktionen- und Relationenalgebren. Boston: Birkhäuser.

    Google Scholar 

  22. Schaefer, T. J. (1978). The complexity of satisfiability problems. In Proceedings of the ACM symposium on theory of computing (STOC), pp. 216–226.

Download references

Author information

Authors and Affiliations

  1. Laboratoire d’informatique (LIX), École Polytechnique, Paris, France

    Manuel Bodirsky

  2. Departament de Tecnologies de la Informació i les Comunicacions, Universitat Pompeu Fabra, Barcelona, Spain

    Hubie Chen

Authors
  1. Manuel Bodirsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hubie Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manuel Bodirsky.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bodirsky, M., Chen, H. Relatively quantified constraint satisfaction. Constraints 14, 3–15 (2009). https://doi.org/10.1007/s10601-008-9054-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10601-008-9054-z

Keywords

Search

Navigation