LinkNet: capturing temporal dependencies among spatial regions

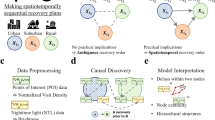
Abstract

Many applications require understanding how event occurrences at one geographical region affect or influence event occurrences at another region, e.g. spread of disease and forest fires. Existing works typically impose a grid to partition the spatial space and utilize spatial autocorrelation property to model the spatial dependency among the grid cells. However, they are often highly sensitive to the granularity of the grid size and they do not incorporate the temporal dynamics of the event occurrences among regions. This paper utilizes the notion of a spatial network with temporal dependency to capture the dynamics of event occurrences among regions. This network is modeled as a directed graph where each node is a group of spatially nearby events and each directed edge represents the influence of events from a source node to a destination node. We design an algorithm called LinkNet to generate this network from spatio-temporal event databases. LinkNet utilizes minimum description length based information–theoretic approach to automatically adjust the number of regions and the temporal relationships among regions. Two optimizations are devised to reduce the computational complexity of LinkNet. We also demonstrate how the proposed network can be used for hotspot prediction. Experiment results on both synthetic and real world datasets demonstrate the efficiency of LinkNet and the effectiveness of the network in predicting the next hotspots.

Appendix

This appendix provides the mathematical proofs of the theoretical results discussed in Sect. 4.

1.1 Appendix 1: Proof for Theorem 1

Proof

$$\begin{aligned}&\sum _{p \in R} Dist(p,R)^2\nonumber \\&\quad = \sum _{p \in R} \left( (p \cdot x-R \cdot x)^2 + (p \cdot y-R \cdot y)^2\right) \nonumber \\&\quad = \sum _{p \in R} \left( p \cdot x^2+p \cdot y^2\right) + \sum _{p \in R} \left( R \cdot x^2-2(p \cdot x)(R \cdot x)\right) \nonumber \\&\qquad + \sum _{p \in R} \left( R \cdot y^2-2(p \cdot y)(R \cdot y)\right) \nonumber \\&\quad = \sum _{p \in R} \left( p \cdot x^2+p \cdot y^2\right) + \left( |R|(R \cdot x^2)-2(R \cdot x)\sum _{p \in R}(p \cdot x)\right) \nonumber \\&\qquad +\left( |R|(R \cdot y^2)-2(R \cdot y)\sum _{p \in R}(p \cdot y)\right) \nonumber \\&\quad = \sum _{p \in R} \left( p \cdot x^2+p \cdot y^2\right) + \left( -|R|(R \cdot x^2)\right) + \left( -|R|(R \cdot y^2)\right) \nonumber \\&\quad = \sum _{p \in R} \left( p \cdot x^2 + p \cdot y^2\right) - |R| \left( R \cdot x^2 + R \cdot y^2\right) \nonumber \end{aligned}$$

This proved the theorem. $\square$

1.2 Appendix 2: Proof for Eq. (1)

Proof

Recall, $|V'|$ = $|V|-1$.

$$\begin{aligned}&NodeGain(R_i, R_j) \nonumber \\&\quad NodeCost(V,D) - NodeCost(V',D) \nonumber \\&\quad = \left( L(V) + L(D|V)\right) - \left( L(V') + L(D|V')\right) \nonumber \\&\quad = \left( \mathrm{log}{|V|}-\mathrm{log}{|V'|} + k|V| - k|V'| \right) \nonumber \\&\qquad + \left( |R_i|\mathrm{log}\frac{|D|}{|R_i|}+|R_j|\mathrm{log}\frac{|D|}{|R_j|}-|R_{ij}|\mathrm{log}\frac{|D|}{|R_{ij}|}\right) \nonumber \\&\qquad +\, \frac{1}{2\sigma ^2\mathrm{ln}2} \left( \sum _{p \in R_i} Dist(p,R_i)^2 + \sum _{p \in R_j} Dist(p,R_j)^2 - \sum _{p \in R_{ij}} Dist(p,R_{ij})^2\right) \nonumber \\ \end{aligned}$$

(5)

The sum of squares of the distances in Eq. (5) can be simplified as follows:

$$\begin{aligned}&\sum _{p \in R_i} Dist(p,R_i)^2 + \sum _{p \in R_j} Dist(p,R_j)^2 - \sum _{p \in R_{ij}} Dist(p,R_{ij})^2 \nonumber \\&\quad = \left( |R_{ij}|(R_{ij} \cdot x^2)-|R_{i}|(R_{i} \cdot x^2)-|R_{j}|(R_{j} \cdot x^2)\right) \nonumber \\&\qquad + \left( |R_{ij}|(R_{ij} \cdot y^2)-|R_{i}|(R_{i} \cdot y^2)-|R_{j}|(R_{j} \cdot y^2)\right) \nonumber \\&\quad =\left( \frac{\left( \sum _{p \in R_i} p \cdot x + \sum _{p \in R_j} p \cdot x\right) ^2}{|R_{ij}|}-|R_{i}|(R_{i} \cdot x^2)-|R_{j}|(R_{j} \cdot x^2)\right) \nonumber \\&\qquad +\left( \frac{\left( \sum _{p \in R_i} p \cdot y + \sum _{p \in R_j} p \cdot y\right) ^2}{|R_{ij}|}-|R_{i}|(R_{i} \cdot y^2)-|R_{j}|(R_{j} \cdot y^2)\right) \nonumber \\&\quad =\left( \frac{|R_i|^2|R_j|^2}{|R_{ij}|} \left( \frac{R_i \cdot x}{|R_j|}+\frac{R_j \cdot x}{|R_i|}\right) ^2 -|R_{i}|(R_{i} \cdot x^2)-|R_{j}|(R_{j} \cdot x^2) \right) \nonumber \\&\qquad +\left( \frac{|R_i|^2|R_j|^2}{|R_{ij}|} \left( \frac{R_i \cdot y}{|R_j|}+\frac{R_j \cdot y}{|R_i|}\right) ^2 -|R_{i}|(R_{i} \cdot y^2)-|R_{j}|(R_{j} \cdot y^2) \right) \nonumber \\&\quad =\frac{|R_i|^2|R_j|^2}{|R_{ij}|} \left( -\frac{R_i \cdot x^2}{(|R_i|)(|R_j|)}-\frac{R_j \cdot x^2}{(|R_i|)(|R_j|)}+\frac{2(R_i \cdot x)(R_j \cdot x)}{(|R_i|)(|R_j|)}\right) \nonumber \\&\qquad +\frac{|R_i|^2|R_j|^2}{|R_{ij}|} \left( -\frac{R_i \cdot y^2}{(|R_i|)(|R_j|)}-\frac{R_j \cdot y^2}{(|R_i|)(|R_j|)}+\frac{2(R_i \cdot y)(R_j \cdot y)}{(|R_i|)(|R_j|)}\right) \nonumber \\&\qquad = -\frac{|R_i||R_j|}{|R_{ij}|} \left( R_i \cdot x-R_j \cdot x\right) ^2 - \frac{|R_i||R_j|}{|R_{ij}|} \left( R_i \cdot y-R_j \cdot y\right) ^2 \nonumber \\&\qquad = -\frac{|R_i||R_j|}{|R_{ij}|} \left( (R_i \cdot x-R_j \cdot x)^2+(R_i \cdot y-R_j \cdot y)^2\right) \nonumber \\&\qquad =-\frac{|R_i||R_j|}{|R_{ij}|} Dist(R_i,R_j)^2 \nonumber \\&\qquad =-\frac{|R_i||R_j|}{|R_i|+|R_j|} Dist(R_i,R_j)^2 \end{aligned}$$

(6)

By substituting Eq. (6) into Eq. (5), we have

$$\begin{aligned}&NodeGain(R_i, R_j)\nonumber \\&\quad =\left( \mathrm{log}\frac{|V|}{|V'|} + k \right) - \left( \frac{|R_i| |R_j| Dist(R_i,R_j)^2}{(2\sigma ^2\mathrm{ln}2) (|R_i| + |R_j|)}\right) \nonumber \\&\qquad +\left( |R_{ij}| \mathrm{log}(|R_{ij}|) - |R_i| \mathrm{log}(|R_i|) - |R_j| \mathrm{log}(|R_j|) \right) \end{aligned}$$

(7)

This proved the equation. $\square$

1.3 Appendix 3: Proof for Theorem 3

We have used following lemma in Theorem 3 to show that $maxNodeGain(R_i,R_j)$ is an upperbound estimation of $NodeGain(R_i,R)$.

Lemma 1

Let $N$ be a positive integer and $x$ is a variable. The function $f:[1,\infty ] \rightarrow [1,\infty ]$, $f(x)=(N+x)\mathrm{log}(N+x)-x\mathrm{log}(x)-N\mathrm{log}N$ is monotonic increasing.

Proof

To prove that $f$ is monotonic increasing, we will show that the first derivative of $f$ is greater than 0.

$$\begin{aligned} \frac{df(x)}{dx}&= (N+x)\left( \frac{1}{N+x}\right) +\mathrm{log}(N+x)(1)-x\left( \frac{1}{x}\right) -\mathrm{log}(x)\\&= 1+\mathrm{log}(N+x)-1-\mathrm{log}(x) \\&= \mathrm{log}\left( \frac{N}{x}+1\right) \\&= \mathrm{log}(N+q)-\mathrm{log}(q) \\&= \mathrm{log}\left( \frac{N}{x}+1\right) \\&> 0 \end{aligned}$$

Clearly, $\frac{df(x)}{dx}$ $>$ 0. This proved the equation. $\square$

Now, we prove Theorem 3 that is discussed in Sect. 5.1.2.

Proof

Recall that $max\_size$ is the maximum size of any region that appears after and including region $R_j$ on the orderline. This implies $max\_size$ $\ge$ $|R|$. From Lemma 1,

$$\begin{aligned}&(|R_i|+max\_size) \mathrm{log}(|R_{i}|+max\_size) \\&\qquad -\left( |R_i| \mathrm{log}(|R_i|) + (max\_size) \mathrm{log}(max\_size)\right) \\&\quad \ge (|R_i|+|R|) \mathrm{log}(|R_{i}|+|R|) - \left( |R_i| \mathrm{log}(|R_i|) + (|R|) \mathrm{log}(|R|)\right) \end{aligned}$$

Since $min\_size \le |R|$ and $ndist_{ij} \le Dist(R_i,R)$, we have

$$\begin{aligned} \frac{(ndist_{ij}^2) (min\_size) |R_i|}{(2\sigma ^2 \mathrm{ln}2) (|R_i| + max\_size)} \le \frac{\left( Dist(R_i,R)^2\right) |R||R_i|}{(2\sigma ^2 \mathrm{ln} 2) (|R_i| + |R|)} \end{aligned}$$

Therefore,

$$\begin{aligned}&maxNodeGain(R_i,R_j) = \left( \mathrm{log}\frac{|V|}{|V|-1} + k \right) \\&\qquad +\,(|R_i|+max\_size) \mathrm{log}(|R_{i}|+max\_size) \\&\qquad -\,\left( |R_i| \mathrm{log}(|R_i|) + (max\_size) \mathrm{log}(max\_size)\right) \\&\qquad -\, \frac{(ndist_{ij}^2) (min\_size) |R_i|}{2\sigma ^2 \mathrm{ln} 2 (|R_i| + max\_size) } \\&\quad \ge \, \left( \mathrm{log}\frac{|V|}{|V|-1} + k \right) - \frac{|R||R_i|(Dist(R_i,R)^2)}{(2\sigma ^2 \mathrm{ln} 2) (|R_i| + |R|)} \\&\qquad +\, (|R_i|+|R|) \mathrm{log}(|R_{i}|+|R|) - \left( |R_i| \mathrm{log}(|R_i|) + (|R|) \mathrm{log}(|R|)\right) \\&\quad = NodeGain(R_i,R) \end{aligned}$$

This proved the theorem. $\square$

1.4 Appendix 4: Proof for Eq. (3)

Proof

$$\begin{aligned}&EdgeCost(E,D) \!-\! EdgeCost(E',D) \!=\! \left( L(E) \!+\! L(Z|E)\right) \!-\! \left( L(E') + L(Z|E')\right) \nonumber \\&\quad = \left( \mathrm{log}{|E|}-\mathrm{log}{|E'|} + 2k|E| - 2k|E'| \right) \nonumber \\&\qquad + \left( |e_i|\mathrm{log}\frac{|E|}{|e_i|}+|e_j|\mathrm{log}\frac{|E|}{|e_j|}-|e_{ij}|\mathrm{log}\frac{|E|}{|e_{ij}|}\right) \nonumber \\&\qquad +\, \frac{1}{2\sigma ^2\mathrm{ln}2}\left( \sum _{z \in e_i} Dist(z,e_i)^2 + \sum _{z \in e_j} Dist(z,e_j)^2 + \sum _{z \in e_{ij}} Dist(z,e_{ij})^2 \right) \qquad \end{aligned}$$

(8)

We can simplify the sum of squares of distances in Eq. (8):

$$\begin{aligned} \sum _{z \in e_i} Dist(z,e_i)^2 \!+ \!\sum _{z \in e_j} Dist(z,e_j)^2 \!-\! \sum _{z \in e_{ij}} Dist(z,e_{ij})^2 \!=\! \frac{|e_i| |e_j|}{|e_i| + |e_j|} Dist(e_i,e_j)^2\nonumber \\ \end{aligned}$$

(9)

By substituting Eq. (9) into Eq. (8), we have

$$\begin{aligned}&EdgeCost(E,D) - EdgeCost(E',D)\\&\quad = \left( \mathrm{log}\frac{|E|}{|E'|} + 2k\right) + \left( |e_{ij}|\mathrm{log}(|e_{ij}|) - |e_i| \mathrm{log}(|e_i|) - |e_j| \mathrm{log}(|e_j|)\right) \\&\qquad -\left( |e_i| |e_j| \frac{\left( Dist(e_i,e_j)^2\right) }{(2 \sigma ^2 \mathrm{ln}2)(|e_i| + |e_j|) } \right) \end{aligned}$$

This proved the equation. $\square$