Extended meet-in-the-middle attacks on some Feistel constructions

Abstract

We show key recovery attacks on generic balanced Feistel ciphers. The analysis is based on the meet-in-the-middle technique and exploits truncated differentials that are present in the ciphers due to the Feistel construction. Depending on the type of round function, we differentiate and show attacks on two types of Feistels. For the first type, which is one of the most practical Feistels, we show a 5-round distinguisher based on a truncated differential, which allows to launch 6-round and 10-round attacks, for single-key and double-key sizes, respectively. For the second type of Feistels, with round functions that follow the SPN structure composed of linear layers with maximal branch number, based on a 7-round distinguisher we show attacks that reach up to 14 rounds. Our attacks outperform all the known attacks for any key sizes and provide new lower bounds on the number of rounds required to achieve a practical and a secure Feistel. The attacks on first type have been experimentally verified with computer implementations of the attacks on small-state ciphers.

Appendices

Appendix 1: The attacks on Feistel-3 for a class of P-layers

Let us confirm that the 10-round attack on Feistel-3 (and the subsequent extensions) is valid for some cases when the P-layer does not have a maximal branch number. The relaxed requirement on the P-layer can be seen as a full diffusion. Again, the attack is based on a 7-round truncated differential. Let $\mathbf 1$ and $\mathbf 1 '$ be two one-word truncated differences that do not necessarily have the active word at the same position. Let $\mathbf {p}$ and $\mathbf {p'}$ be the truncated differences $P(\mathbf 1 )$ and $P(\mathbf 1 ')$, respectively, and they are active in all words (if not then the time complexity of the attack will increase). Then, the truncated differential has the form:

$$\begin{aligned} (0, \mathbf 1 ) \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf 1 , 0) \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf {p}, \mathbf 1 ) \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf 1 \oplus \mathbf 1 ', \mathbf {p}) \mathop {\longrightarrow }\limits ^{\text {1R}} \\ (\mathbf {p'}, \mathbf 1 \oplus \mathbf 1 ') \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf 1 ', \mathbf {p'}) \mathop {\longrightarrow }\limits ^{\text {1R}} (0, \mathbf 1 ') \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf 1 ', 0). \end{aligned}$$

To avoid possible contradictions in the differential, the P-layer has to satisfy certain conditions. A careful investigation shows that there are two conditions imposed on the P-layer: $P(\mathbf {p}) = \mathbf 1 '$ and $P(\mathbf {p'}) = \mathbf 1$, which reduces to $P(P(\mathbf 1 )) = \mathbf 1 ', P(P(\mathbf 1 ')) = \mathbf 1$. Thus, the assumption of a maximal branch number can be replaced with a somewhat weaker requirement, which broaden the class of P-layers that can be attacked.

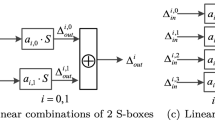
We can proceed as in the original 10-round attack on Feistel-3 (assume that P-layer of round 6 has been moved). To adapt Proposition 2 for this case, we find all possible differences that follow this differential. We fix the input/output difference of the single active words in rounds 2 and 6, the two input differences at round 4 (or one if $\mathbf 1 = \mathbf 1 '$), and the output difference of the S-layer at round 3, i.e. ${\varDelta }F_{i+3}^{\mathcal {M}}$, or in total $2^{6c + n/2}$ differences. This fixes the input and the output differences of all active words to the S-layers in all 7 rounds, and reveals the values of two active words at rounds 2 and 6, two words at round 4, and all words of states at rounds 3 and 5. To construct the b-$\delta$ sequences for each fixed differences, we first guess the remaining inactive words of round 4 (in total $n/2-2c$), and proceed further as in the original attack. Thus, the total time and memory complexity of the offline phase required to construct $T_{\delta }$ is $2^{n/2 + 4c}$ i.e. exactly the same complexities as before. We note that $T_{\delta }$ still has $2^{n/2+4c}$ elements because each word guess corresponds to a different entry in the table.

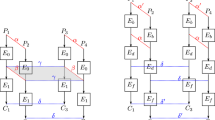
In the data collection phase, the number of collected pairs remains the same as the previous 10-round attack. Recall Fig. 10. The truncated differential for the first round is $(\mathbf 1 , \mathbf {p}) \mathop {\longrightarrow }\limits ^{\text {1R}} (0, \mathbf 1 )$, here $\mathbf {p}$ is not fully active. However, the crucial property i.e. the attacker can collect $2^{4c-1}$ pairs with $2^{2c}$ chosen plaintexts does not change. The truncated differential for the last two rounds of the previous 10-round attack is $(\mathbf 1 , \mathbf 1 ) \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf 1 , \mathbf 1 ) \mathop {\longrightarrow }\limits ^{\text {1R}} (\mathbf {p}, \mathbf {A})$. In this attack, because $\mathbf {p}$ is not fully active, the possible number of differences after the S-layer in the 10th round is smaller than the previous 10-round attack. Suppose that $\mathbf {p}$ activates $\alpha$ S-boxes. Then, the possible number of differences for $v_{10}$ is only $2^{(\alpha +1)c}$, where $2^{\alpha c}$ come from the round function and $2^c$ come from the difference of $v_8$. This limitation of differential space gives the attacker more advantages when he collects the pairs. Namely, he has extra $(n/2 - \alpha c)$-bit filter when he collects the pairs satisfying the differential. Note that the fewer number of pairs in the key recovery phase does not affect to the success probability of the attack. Indeed, the probability of differential cancellation in the last round becomes $2^{-\alpha c + c}$, which is higher than the previous 10-round attack by a factor of $2^{n/2- \alpha c}$. This offsets the smaller number of collected pairs. In the end, the data complexity is exactly the same as the previous attack, and it can filter out more pairs due to the limited differential propagation. Moreover, the success probability remains unchanged from the previous attack. Similarly, the key-recovery phase is exactly the same except that we can recover all words of $K_9$ except the non-active words. As a result, the whole attack has precisely the same time, data and memory complexities as the original attack on 10-round Feistel-3, where the P-layer has a maximal branch number.

Appendix 2: Recovering all subkeys

In Sects. 3 and 4, we have shown attacks that recover some subkeys (full values and words). Since our attack is generic and nothing has been assumed on the key schedule, there is a possibility that the knowledge of a subkey does not result in easily computable reduction of the master key space, for instance the case of non-invertible key schedule. An alternative is to recover all the subkeys of the cipher, which also allows the attacker to encrypt or decrypt any plaintext or ciphertext of his/her choice. In this section, we show how all the subkeys can be recovered.

One may note that it is possible to introduce time/memory/data tradeoff here, by reducing the matching bits from b-$\delta$-set or by making use of less data for the matching. Note the maximum reduction is limited by a factor of $2^b$, which is about n, significantly smaller than the overall complexities of order $2^n$. Hence, we do not give the details for this tradeoff here.

1.1 Feistel-2

It is important to note that in all our attacks on Feistel-2, the first round subkey $K_0$ is recovered. With the knowledge of $K_0$, we can either repeat the same procedure or re-use other existing methods to attack a sub-cipher $E_1$ which is exactly the entire cipher but with the first round removed. Since there is a bijective mapping between $(v_0, v_{-1})$ and $(v_1, v_0)$, and it is easily computable in both directions with the knowledge of $K_0$, i.e., it is easy to compute the plaintext ($v_1, v_0$) of $E_1$ from the plaintext ($v_0, v_{-1}$) of the original Feistel-2 cipher and vice versa, one will not have problem choosing the plaintext to $E_1$.

The cipher with one less round can be attacked with significantly lower complexities which eventually becomes negligible compared with that for the original attacks. For example, in our 6-round key-recovery attack for Feistel-2 with $k=n$ as in Sect. 3, besides other choices, the attacker can re-use the results in [18] on 5-round Feistel-2 to recover $K_1, K_2, \ldots , K_5$ in time $2^{n/2}$, compared with $2^{3n/4}$ for 6-round attack to recover $K_0$. Hence, the complexities for recovering all subkeys remain unchanged.

For the extended attacks to larger key sizes, one can always prepend or append less rounds to the distinguisher and result in faster attacks when $K_0$ is recovered, using similar attack procedure, for the cases where reduced cipher is of more than 6 rounds.⁷

1.2 Feistel-3

In the case of Feistel-3, the same method can be applied, except now it is the last round subkey which is recovered instead of the $K_0$. So here, instead of the first round, we remove the last round, and with the knowledge of the subkey of the last round, there is an easily computable bijective mapping between the ciphertext of the original cipher and ciphertext of the reduced cipher.

Appendix 3: Experimental verification of the attacks on Feistel-2

To check the correctness of our attacks we have implemented and applied them to small state ciphers. The ciphers were designed to follow the generic constructions and the state size was chosen to make the attacks feasible in real time. The codes were written in C++ and complied with g++ on Linux. The source code for the two experiments are available for 6 rounds: http://www1.spms.ntu.edu.sg/~syllab/attacks/F2-6rounds.tar.gz, and for 8 rounds: http://www1.spms.ntu.edu.sg/~syllab/attacks/F2-8rounds.tar.gz.

We first implemented the 6-round key recovery attack on Feistel-2. The outputs of the round functions were chosen as random values produced from a pseudo random number generator, and saved in tabular form. We tested the attack on Feistels with key and block sizes of 24 bits, i.e. $k=n=24$, while the value of $x'$ (as suggested by the attack) was set to 6, i.e. $x'=n/4=6$. We ran 1000 experiments for this cipher, and in each of them the subkeys were chosen at random. The program produced the following output:

Obviously the size of $T_{\delta }$ and the number of the collected pairs matches the estimates predicted by the attack.

Our attack theory shows that among the collected $2^{12.0}$ pairs, if there is at least one pair satisfying the truncated differential, the secret key will be recovered. Further more, by using more data, the success probability of the attack, i.e. the probability of collecting a pair satisfying the truncated differential, can increase.

The experiment shows that, with $2^{12.0}$ pairs, in 59 % of the cases the collected pairs were able to reveal the secret key, and in such cases, the attack succeeded with 100 % rate. For the courtesy, in our second series of 1000 experiment we took twice larger data set, and in this case around 90 % of the keys were recovered, again with 100 % success rate. Finally, when the data was four times larger than the initially suggested, the former percentage increased to 97 %. Thus we can conclude that the 6-round key recovery is correct.⁸

We then tested the extension of the above attack to 8 rounds as described in the paper. The round function was chosen similarly, the state size was set to 18 bits, and the key size to 27 bits, i.e. $n=18, k=27$. As the suggested value of $x'$ is n / 3, we took $x'=6$. We ran 100 experiments, and the resulting output was as follow:

The results were similar as in the case above. The small deviation in the number of predicted pairs comes from the fact that ${2}^{d}$ data results in around ${2}^{2d-1}$ pairs, thus instead of ${2}^{18}$ pairs, in practice we have obtained ${2}^{17}$, which in turn explains the smaller percentage of recovered keys. Once we took twice larger data set, the percentage increased to 81 %. Thus the attack works as predicted.