Separating invertible key derivations from non-invertible ones: sequential indifferentiability of 3-round Even–Mansour

Abstract

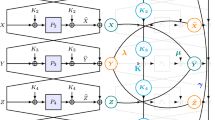
Iterated Even–Mansour (IEM) scheme consists of a small number r of fixed n-bit permutations separated by $r+1$ round-key additions. When the permutations are public, independent and random, and a common round key derived from the master key by an idealized non-invertible key derivation (KD) function is used, 5 rounds was proved sufficient to obtain (full) indifferentiability from ideal ciphers by Andreeva et al. (CRYPTO 2013). The KD can be a random oracle, or a Davies-Meyer construction from a random permutation. This work considers such IEM with non-invertible KD in the sequential indifferentiability model of Mandal et al. (TCC 2012). As results, this work shows that in both cases mentioned before, 3 rounds yields sequential indifferentiability from ideal ciphers. As Andreeva et al. has proved 3-round IEM with idealized invertible key derivations not sequentially indifferentiable (by exhibiting an attack), a definitive separation between IEM with invertible key derivations and IEM with non-invertible key derivations is established. This is the most important implication of the results in this work.

Appendices

Appendix 1: Deferred proofs for $\text {EMR}_3$

1.1 Two other helper lemmas

The first helper lemma claims that the simulator really gives answers consistent with ${\mathbf {E}}$.

Lemma 11

For any good $\varSigma _2$-tuple $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$, D obtains the same answer for any query to ${\mathbf {E}}$/${EMR }_3^{{\mathbf {S}}^{\alpha }}$ in the two executions $D^{\varSigma _1(\alpha )}$ and $D^{\varSigma _2(\alpha )}$.

Proof

In $D^{\varSigma _2(\alpha )}$, each time D issues a query $(K,y_0)$ to $\text {EMR}_3$, $\text {EMR}_3$ will query ${\mathbf {S}}^{\alpha }.\text {H}(K)$ and ${\mathbf {S}}^{\alpha }.\text {P}(2,+,x_2)$ (for the corresponding $x_2$), so that after $\text {EMR}_3$ answers this query, it holds $(K,k)\in KSet$ and $(x_2,y_2)\in P_2$. By this, the query ${\mathbf {S}}.\text {H}(K)$ and the query ${\mathbf {S}}.\text {P}(2,\delta ,x_2)$ must have appeared during $D^{\varSigma _2(\alpha )}$, and the one appeared later would trigger a call to ${\mathbf {S}}.\text {Complete}$, after which the answer of $\text {EMR}_3$ (computed from the tables $\{P\}$ of ${\mathbf {S}}$) would have been consistent with ${\mathbf {E}}$. This establishes the claim, since the answer in $D^{\varSigma _1(\alpha )}$ is directly given by ${\mathbf {E}}$. $\square$

The second one is an inequality. It uses a new notation $\varTheta _1$, which is based on a corollary of Lemma 8. For this, consider a tuple of sets $\gamma \in {\mathcal {T}}$, and assume that the following hold for a tuple of primitives $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$:

• $D^{\varSigma _2(\alpha )}\rightarrow \gamma$;

• D outputs 1 in $D^{\varSigma _2(\alpha )}$, say, $D^{\varSigma _2(\alpha )}=1$.

Then by Lemma 8, for any tuple $\alpha '=({\mathbf {E}}',{\mathbf {H}}',{\mathbf {P}}')$, once $D^{\varSigma _2(\alpha ')}\rightarrow \gamma$, $D^{\varSigma _2(\alpha ')}=1$ – to this end, consider a tuple $\beta =({\mathbf {H}},{\mathbf {P}})\cong \gamma$, then $1=D^{\varSigma _2(\alpha )}=D^{\varSigma _3(\beta )}=D^{\varSigma _2(\alpha ')}$. With this in mind, the notation $\varTheta _1$ is used to denote the subset of ${\mathcal {T}}$ such that for any $\alpha$ such that $D^{\varSigma _2(\alpha )}\rightarrow \gamma \in \varTheta _1$ it holds $D^{\varSigma _2(\alpha )}=1$.

Lemma 12

$Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3({\mathbf {H}},{\mathbf {P}})}=1]\ge \sum _{\gamma \in \varTheta _1} Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ]$.

Proof

We show that for any tuple $({\mathbf {H}}^{*},{\mathbf {P}}^{*})$, there exists at most one $\gamma \in {\mathcal {T}}$ s.t. $({\mathbf {H}}^{*},{\mathbf {P}}^{*})\cong \gamma$. Assume otherwise, i.e. $\exists \gamma '\in {\mathcal {T}}$ s.t. $\gamma \ne \gamma '\wedge ({\mathbf {H}}^{*},{\mathbf {P}}^{*})\cong \gamma \wedge ({\mathbf {H}}^{*},{\mathbf {P}}^{*})\cong \gamma '$. Assume that for two good tuples $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and $\alpha '=({\mathbf {E}}',{\mathbf {H}}',{\mathbf {P}}')$, it holds $D^{\varSigma _2(\alpha )}\rightarrow \gamma$ and $D^{\varSigma _2(\alpha ')}\rightarrow \gamma '$. Then, consider any query of the combination $(D,{\mathbf {S}})$ in the two executions $D^{\varSigma _2(\alpha )}$ and $D^{\varSigma _2(\alpha ')}$: (i) the answers to the query to ${\mathbf {H}}$/${\mathbf {H'}}$ are the same, since ${\mathbf {H}}.\text {H}(K)={\mathbf {H}}^{*}.\text {H}(K)={\mathbf {H}}'.\text {H}(K)$; (ii) similarly, the answers to the query to ${\mathbf {P}}$/${\mathbf {P'}}$ are the same; (iii) the answers to the query to ${\mathbf {E}}$/${\mathbf {E'}}$ are also the same. For this, first, by Lemma 11, the answers of ${\mathbf {E}}$/${\mathbf {E'}}$ equal the answers of $\text {EMR}_3$ in the two $\varSigma _2$ executions; second, the answers of $\text {EMR}_3$ are computed from the sets $\gamma$ and $\gamma '$ respectively; third, the corresponding entries in $\gamma$ and $\gamma '$ have the same contents, since both of them coincide with the contents of $({\mathbf {H}}^{*},{\mathbf {P}}^{*})$. Then, following the same line as the proof of Lemma 8, we have that the transcripts of the combination $(D,{\mathbf {S}})$ in the two executions $D^{\varSigma _2(\alpha )}$ and $D^{\varSigma _2(\alpha ')}$ are the same, so that the two set-tuples $\gamma$ and $\gamma '$ should be the same, a contradiction. After this, we have

$$\begin{aligned} Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3({\mathbf {H}},{\mathbf {P}})}=1]&\ge Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3({\mathbf {H}},{\mathbf {P}})}=1 \wedge \exists \gamma \in {\mathcal {T}}\text { s.t. }({\mathbf {H}},{\mathbf {P}})\cong \gamma ] \\&= \sum _{\gamma \in \varTheta _1} Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ] \text { (by Lemma 8)}. \end{aligned}$$

as claimed. $\square$

The (analogues of) the two helper lemmas also hold in the context of $\text {EMDP}_3$. The proofs can be obtained by make very little modifications on the two proofs above, thus omitted.

1.2 Proof of Lemma 8

By an induction, assume that the transcripts obtained by D are the same up to some point in the three executions, and consider the next query of D. Since D is deterministic, the next query in the three executions are the same. We argue that the answers obtained in the three executions are the same. Depending on the type of this query, we distinguish three cases:

• (i) the query is to $\text {H}$: then since ${\mathbf {S}}$ only relays the answers of ${\mathbf {H}}^{\alpha }$, the answers obtained in $D^{\varSigma _1({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ and $D^{\varSigma _2({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ are the same; and since ${\mathbf {H}}^{\beta }$ extends the set KSet of ${\mathbf {S}}^{\alpha }$, the answers obtained in $D^{\varSigma _2({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ and $D^{\varSigma _3({\mathbf {H}}^{\beta },{\mathbf {P}}^{\beta })}$ are also the same;

• (ii) the query is to $\text {P}$: then in $D^{\varSigma _1(\alpha )}$ and $D^{\varSigma _2(\alpha )}$, the query must be made during the first phase (in which D only queries $\text {H}$ and $\text {P}$). It can be easily seen that this part of $D^{\varSigma _1(\alpha )}$ is exactly the same as that of $D^{\varSigma _2(\alpha )}$, so that the answers obtained are the same. On the other hand, the answers obtained in $D^{\varSigma _2({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ and $D^{\varSigma _3({\mathbf {H}}^{\beta },{\mathbf {P}}^{\beta })}$ are also the same since ${\mathbf {P}}^{\beta }$ extends the set $\{P\}$ of ${\mathbf {S}}^{\alpha }$;

• (iii) the query is to $\text {E}$: then due to Lemma 11, the answers obtained in $D^{\varSigma _1(\alpha )}$ and $D^{\varSigma _2(\alpha )}$ are the same. Also, the answers obtained in $D^{\varSigma _2(\alpha )}$ and $D^{\varSigma _3(\beta )}$ are the same, since the function/permutation values used by $\text {EMR}_3$ to compute the answers are the same.

Therefore, the three transcripts of D are the same. Since D is deterministic, the three outputs of D are also the same.

1.3 Proof of Lemma 9

Let $\gamma =\{KSet,\{P\}\}$ and $\{P\}=\{P_1,P_2,P_3\}$. Then clearly $Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ]= (\frac{1}{2^n})^{|KSet|} \cdot (\prod _{j=0}^{|P_1|-1}\frac{1}{2^n-j}) \cdot (\prod _{j=0}^{|P_2|-1}\frac{1}{2^n-j}) \cdot (\prod _{j=0}^{|P_3|-1}\frac{1}{2^n-j})$.

As to $Pr[D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma ]$, consider a good tuple $\alpha =({\mathbf {E}}',{\mathbf {H}}',{\mathbf {P}}')$ which satisfies $D^{\varSigma _2(\alpha )}\rightarrow \gamma$. It can be easily checked that $D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma$ if and only if the transcripts of the combination $(D,{\mathbf {S}})$ in ${D}^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$ and ${D}^{\varSigma _2(\alpha )}$ are the same,⁸ i.e. the random values accessed during ${D}^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$ are exactly the same as those accessed during ${D}^{\varSigma _2(\alpha )}$. Assume that during $D^{\varSigma _2(\alpha )}$, there are u (v, resp.) entries in $P_1$ ($P_3$, resp.) that are defined by calling ${\mathbf {P}}'$, and let $w=|ESet|$. Then we have

$$\begin{aligned}&Pr[D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma ] \\&\quad \le (\frac{1}{2^n})^{|KSet|} \cdot \left( \prod _{j=0}^{u-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{|P_2|-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{v-1}\frac{1}{2^n-j}\right) \cdot \left( \frac{1}{2^n-w}\right) ^w. \end{aligned}$$

Since each adaptation (either in $P_1$ or in $P_3$) uniquely corresponds to an execution of $\text {Complete}$ (by construction) and the latter uniquely corresponds to an entry in ESet (by Lemma 2), we have $u+v+w=|P_1|+|P_3|$. Moreover we have $|P_1|\ge u$, $|P_3|\ge v$, and $w\le q^2$ (Lemma 1), hence

$$\begin{aligned} \frac{Pr_{{\mathbf {H}},{\mathbf {P}}}[\left( {\mathbf {H}},{\mathbf {P}}\right) \cong \gamma ]}{Pr_{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _2\left( {\mathbf {E}},{\mathbf {H}},{\mathbf {P}}\right) }\rightarrow \gamma ]}&\ge \frac{\left( \prod _{j=0}^{|P_1|-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{|P_3|-1}\frac{1}{2^n-j}\right) }{\left( \prod _{j=0}^{u-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{v-1}\frac{1}{2^n-j}\right) \cdot \left( \frac{1}{2^n-w}\right) ^w} \\&\ge \frac{\left( \frac{1}{2^n}\right) ^{w}}{\left( \frac{1}{2^n-w}\right) ^{w}} \ge 1-\frac{w^2}{2^n} \ge 1-\frac{q^4}{2^n}. \end{aligned}$$

as claimed.

1.4 Proof of Lemma 10

Let $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and $\beta =({\mathbf {H}},{\mathbf {P}})$. Recall from Sect. 3.4.2 that the event “$\alpha$ bad” means that ${\mathbf {S}}^{\alpha }$ aborts during the $\varSigma _2$ execution $D^{\varSigma _2(\alpha )}$, while “$\alpha$ good” means otherwise. Furthermore, let $\varTheta _1$ be the subset of ${\mathcal {T}}$ such that for any $\alpha$ such that $D^{\varSigma _2(\alpha )}\rightarrow \gamma \in \varTheta _1$ it holds $D^{\varSigma _2(\alpha )}=1$ (same as Appendix 1). Then, wlog assume that $Pr_{\alpha }[D^{\varSigma _1(\alpha )}=1]\ge Pr_{\beta }[D^{\varSigma _3(\beta )}=1]$, it holds

$$\begin{aligned}&\left| Pr_{\beta } [D^{\varSigma _3(\beta )}=1] - Pr_{\alpha }[D^{\varSigma _1(\alpha )}=1] \right| \\&\quad = \underbrace{Pr_{\alpha }[\alpha \text { bad}\wedge D^{\varSigma _1(\alpha )}=1]}_{\le Pr[\alpha \text { bad}]\le \frac{17q^4}{2^n}\text { (Lemma 7)}} + Pr_{\alpha }[\alpha \text { good}\wedge D^{\varSigma _1(\alpha )}=1] - \underbrace{Pr_{\beta }[D^{\varSigma _3(\beta )}=1].}_{\ge \sum _{\gamma \in \varTheta _1}Pr_{\beta }[\beta \cong \gamma ]\text { (Lemma 12)}} \end{aligned}$$

By Lemma 8, when $\alpha$ is good, $D^{\varSigma _1(\alpha )}=D^{\varSigma _2(\alpha )}$. Hence we have

$$\begin{aligned}&Pr_{\alpha }[\alpha \text { good}\wedge D^{\varSigma _1(\alpha )}=1] = Pr_{\alpha }[\alpha \text { good}\wedge D^{\varSigma _2(\alpha )}=1] = \sum _{\gamma \in \varTheta _1} Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ], \end{aligned}$$

and

$$\begin{aligned}&\left| Pr_{\beta } [D^{\varSigma _3(\beta )}=1] - Pr_{\alpha }[D^{\varSigma _1(\alpha )}=1] \right| \\&\quad \le \frac{17q^4}{2^n} + \sum _{\gamma \in \varTheta _1} \left( Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ] - \underbrace{Pr_{\beta }[\beta \cong \gamma ]}_{\ge (1-\frac{q^4}{2^n})Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ] \text { (Lemma 9)} } \right) \\&\quad \le \frac{17q^4}{2^n} + \sum _{\gamma \in \varTheta _1} \frac{q^4}{2^n} \cdot Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ] \le \frac{18q^4}{2^n} \end{aligned}$$

as claimed.

Appendix 2: Andreeva et al.’s seq-distinguisher on 3-round Even–Mansour with invertible KD [2]

Consider the 3-round Even–Mansour with an invertible KD function ${\mathbf {IKD}}$:

$$\begin{aligned} \text {EMIKD}_{3}(K,m)={\mathbf {IKD}}(K)\oplus {\mathbf {P}}_{3}({\mathbf {IKD}}(K)\oplus {\mathbf {P}}_{2}({\mathbf {IKD}}(K)\oplus {\mathbf {P}}_{1}({\mathbf {IKD}}(K)\oplus m))), \end{aligned}$$

the (seq-)distinguisher D works as follows (the notations have been adapted to the convention used in this paper):

• (1) D queries ${\mathbf {P}}_1$ on some arbitrary $x_1$: $y_1:={\mathbf {P}}_1(x_1)$.

• (2) For two distinct, arbitrarily chosen keys $K_1$ and $K_2$, D queries $k_1:={\mathbf {IKD}}(K_1)$ and $k_2:={\mathbf {IKD}}(K_2)$.

• (3) D queries ${\mathbf {P}}_2$: $x_2:=y_1\oplus k_1$, $y_2:={\mathbf {P}}_2(x_2)$, and $x_2':=y_1\oplus k_2$, $y_2':={\mathbf {P}}_2(x_2')$; queries ${\mathbf {P}}_3$: $x_3:=y_2\oplus k_1$, $y_3:={\mathbf {P}}_3(x_3)$, and $x_3':=y_2'\oplus k_2$, $y_3':={\mathbf {P}}_3(x_3')$ (notice that D’s objective is to compute two distinct values $y_3$ and $y_3'$, namely two diverging paths connected only under the ${\mathbf {P}}_1$ evaluation).

• (4) D sets $k_3:=y_2\oplus x_3'$ and $k_4:=y_2'\oplus x_3$, and queries ${\mathbf {IKD}}$: $K_3:={\mathbf {IKD}}^{-1}(k_3)$ and $K_4:={\mathbf {IKD}}^{-1}(k_4)$.

• (5) D computes using inverse queries to $E(-,\cdot ,\cdot )$: $x_1':=E(-,K_3,y_3'\oplus k_3)\oplus k_3$ and $x_1'':=E(-,K_4,y_3\oplus k_4)\oplus k_4$.

• (6) If $x_1'=x_1''$, then D guesses the real world and otherwise the simulated.

A (seq-)distinguisher based on the same principle was exhibited by Lampe and Seurin [26], which finds an evasive relation between the inputs and outputs of $\text {SEM}_{3}$.