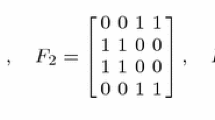Abstract
This paper is concerned with constructions and orthogonality of generalized Sudoku arrays of various forms. We characterize these arrays based on their constraints; for example Sudoku squares are characterized by having strip and sub-square constraints. First, we generalize Sudoku squares to be multi-dimensional arrays with strip and sub-cube constraints and construct mutually orthogonal sets of these arrays using linear polynomials. We add additional constraints motivated by elementary intervals for low discrepancy sequences and again give a construction of these arrays using linear polynomials in detail for 3 dimensional and a general construction method for arbitrary dimension. Then we give a different construction of these hypercubes due to MDS codes. We also analyze the orthogonality of all of the Sudoku-like hypercubes we consider in this paper.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bailey R.A., Cameron P., Connelly R.: Sudoku. Gerechte designs, resolutions, affine space, spreads, reguli and Hamming codes. Am. Math. Monthly 115, 383–404 (2008).
Bar-Yahalom E., Etzion T.: Intersection of isomorphic linear codes. J. Comb. Theory Ser. A 80, 247–256 (1997).
Beutelspacher A., Rosenbaum U.: Projective Geometry: From Foundations to Applications. Cambridge University Press, Cambridge (1998).
Bose R.C.: Mathematical theory of the symmetrical factorial design. Sankhyä 8, 107–166 (1947).
Chao J.M., Kaneta H.: Classical arcs in \(\text{ PG }(r, q)\) for \(11 \le q \le 19\). Discret. Math. 174, 87–94 (1997).
Chao J.M., Kaneta H.: Classical arcs in \(\text{ PG }(r, q)\) for \(23 \le q \le 29\). Discret. Math. 226, 377–385 (2001).
Donovan D., Haaland B., Nott D.J.: A Simple Approach to Constructing Quasi-Sudoku-based Sliced Space-Filling Designs, p. 15. arXiv:1502.05522 (2015).
Ethier J.T., Mullen G.L., Panario D., Stevens B., Thomson D.: Sets of orthogonal hypercubes of class \(r\). J. Comb. Theory (Ser. A) 119, 430–439 (2012).
Hamner, III J.M.: Taking Sudoku puzzles a step further: an existential problem (research talk). In: Forty-Sixth Southeastern International Conference on Combinatorics, Graph Theory, and Computing, Boca Raton, FL (2015).
Huffman W.C., Pless V.: Fundamentals of Error-Correcting Codes. Cambridge University Press, Cambridge (2003).
Kishen K.: On the construction of Latin and hyper-Graeco-Latin cubes and hypercubes. J. Indian Soc. Agric. Stat. 2, 20–48 (1950).
Lawrence K.M.: A combinatorial characterization of \((t, m, s)\)-nets in base \(b\). J. Comb. Des. 4, 275–293 (1996).
Lidl R., Niederreiter H.: Finite Fields, 2nd edn. Cambridge University Press, Cambridge (1997).
Mullen G.L., Panario D. (eds.): Handbook of Finite Fields. CRC Press, Boca Raton (2013).
Mullen G.L., Whittle G.: Point sets with uniformity properties and orthogonal hypercubes. Monatsh. Math. 113, 265–273 (1992).
Niederreiter H.: Random Number Generation and Quasi-Monte Carlo Methods. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (1992).
Panario D., Thomson D.: Efficient \(p\)th root computations in finite fields of characteristic \(p\). Des. Codes Cryptogr. 62, 273–283 (2011).
Tovstik T.M.: Calculation of the discrepancy of a finite set of points in the unit \(n\)-cube. Vestnik St. Petersb. Univ. Math. 40, 250–252 (2007).
Acknowledgments
We greatly acknowledge George Andrews and James Sellers for their help identifying and proving the results in Lemma 6. We would also like to thank Daniel Panario for presenting these results on our behalf at the 2015 ALCOMA conference in Kloster Banz, Germany. Finally, we would like to thank the two anonymous referees for their helpful suggestions and corrections.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. J. Colbourn.
This work was completed while the first and fourth authors were at the School of Mathematics and Statistics at Carleton University.
Rights and permissions
About this article
Cite this article
Huggan, M., Mullen, G.L., Stevens, B. et al. Sudoku-like arrays, codes and orthogonality. Des. Codes Cryptogr. 82, 675–693 (2017). https://doi.org/10.1007/s10623-016-0190-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-016-0190-y