Modeling and Analysis of Link Duration in Vehicular Ad Hoc Networks Under Different Fading Channel Conditions

Abstract

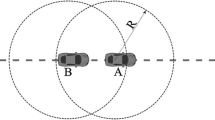
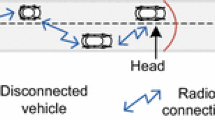
Modeling and analysis of communication link duration in vehicular ad hoc networks (VANETs) is crucial as it directly affects many performance metrics such as packet delivery ratio, throughput and end-to-end delay. In this paper, we investigate the properties of communication link duration in one-dimensional VANETs for different fading channel conditions. We employ a stochastic microscopic mobility model that takes into account time dependence of the inter-vehicle distance. A discrete-time finite-state Markov chain with state dependent transition probabilities is used to model the inter-vehicle distance. The presence of fading channel conditions will introduce fluctuations in the received signal power. Even when the inter-vehicle distance between a given pair of vehicles is less than their transmission range, poor channel conditions may result in link failure. A modified distance transition probability matrix is derived to describe the combined effects of relative velocity among a pair of vehicles, link failure due to outage, and inter-vehicle distance. The probability distribution of the communication link duration is derived from the modified distance transition probability matrix. The analytical results obtained from the model are validated by extensive simulation results.

Appendix 1

Derivation of  (2):

Since $V_r = V_A - V_B$, the dynamic range of $V_r$ is limited to ($-v_m,v_m$) where $v_m=v_{max}-v_{min}$. The CDF $F_{V_r}{(v_r)}$ can be determined as follows:

$$\begin{aligned} F_{V_r}{(v_r)}=P(V_r\le v_r) =P(V_A - V_B\le v_r) \end{aligned}$$

(35)

Using the principle of random variable transformation [35], $F_{V_r}{(v_r)}$ can be determined as follows:

$$\begin{aligned} F_{V_r}{(v_r)}=\left\{ \begin{array}{ll} \int _{v_A = v_{min}}^{v_r + v_{max}} \! \int _{v_B = v_A - v_r}^{v_{max}} \! f_{V_A,V_B}(v_A, v_B) \,\,\mathrm {d} v_B \,\,\mathrm {d} v_A ;&{}\quad -v_m\le v_r\le 0\\ 1- \int _{v_A = v_r + v_{min}}^{v_{max}} \! \int _{v_B = v_{min}}^{v_A - v_r} \! f_{V_A,V_B}(v_A, v_B) \,\,\mathrm {d} v_B \,\,\mathrm {d} v_A ;&{} \quad 0\le v_r\le v_m \end{array}\right. \end{aligned}$$

(36)

The PDF of $V_r, f_{V_r}(v_r)$ is obtained by differentiating (36) with respect to $v_r$ and is given by:

$$\begin{aligned} f_{V_r}{(v_r)}=\left\{ \begin{array}{ll} \frac{d}{dv_r}\int _{v_A = v_{min}}^{v_r + v_{max}} \! \int _{v_B = v_A - v_r}^{v_{max}} \! f_{V_A,V_B}(v_A, v_B) \,\,\mathrm {d} v_B \,\,\mathrm {d} v_A ;&{} \quad -v_m\le v_r\le 0\\ 0-\frac{d}{dv_r} \int _{v_A = v_r + v_{min}}^{v_{max}} \! \int _{v_B = v_{min}}^{v_A - v_r} \! f_{V_A,V_B}(v_A, v_B) \,\,\mathrm {d} v_B \,\,\mathrm {d} v_A ;&{} \quad 0\le v_r\le v_m \end{array}\right. \end{aligned}$$

(37)

In the free flow traffic state, each vehicle moves independently of others. Hence $f_{V_A,V_B}(v_A, v_B)=f_{V_A}(v_A)\times f_{V_B}(v_B)$. Further $V_A$ and $V_B$ are Uniform over ($v_{min},v_{max}$). Hence the above integral can be simplified to get the following expression for $f_{V_r}(v_r)$:

$$\begin{aligned} f_{V_r}(v_r)=\left\{ \begin{array}{ll} \frac{v_r +v_{max}-v_{min}}{(v_{max}-v_{min})^2};&{}\,-v_m\le v_r \le 0 \\ \frac{v_{max}-v_{min}-v_r }{(v_{max}-v_{min})^2};&{}\,\,0 \le v_r \le v_m \\ \end{array}\right. \end{aligned}$$

(38)

1.1 Appendix 2

Derivation of (23):

The integral in the (23) can be written as:

$$\begin{aligned} \begin{aligned} \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon }P_{out}(P_{min},x)\,dx&= \quad\frac{1}{2\varepsilon }\int \limits _{(i-1)\varepsilon }^{i\varepsilon } \left[ 1+erf\left( \frac{P_{min}-(P_t+10log_{10}k-10\alpha log_{10}\left( \frac{x}{d_0}\right) }{\sqrt{2}\sigma _{\psi _{dB}}}\right) \right] \,dx\\ \end{aligned} \end{aligned}$$

(39)

Let $a=P_{min}-P_t-10logk, b=\sqrt{2}\sigma _{\psi _{dB}}$ and $c=d_0$ and performing integration by parts

$$\begin{aligned} \begin{aligned} \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon }P_{out}(P_{min},x)\,dx\,=\,&\frac{1}{2\varepsilon } \left[ x+x\,erf\left( \frac{a+10\alpha log_{10}(\frac{x}{c})}{b}\right) \right. \\&\left. + \int \limits _{(i-1)\varepsilon }^{i\varepsilon } \frac{20\alpha e^{(-\frac{a+10\alpha log_{10}\left( \frac{x}{c}\right) }{b})}}{b\sqrt{\pi }}\,dx \right] _{((i-1)\varepsilon )}^{(i\varepsilon )} \end{aligned} \end{aligned}$$

(40)

Integrating and substituting the limits, the following result is obtained:

$$\begin{aligned} \begin{aligned} E [P_{out}(i)] =&\frac{1}{2\varepsilon }\left[ \varepsilon -i\varepsilon \left( erf\left( \frac{a+10\alpha log\frac{(i-1)\varepsilon }{c}}{b}\right) -erf\left( \left( \frac{a+10\alpha log\frac{i\varepsilon }{c}}{b}\right) \right) \right) \right. \\&+ \varepsilon \,erf\left( \left( \frac{a+10\alpha log\frac{i\varepsilon }{c}}{b}\right) \right) + c\,e^{\frac{1}{400}\left( \frac{b^2}{\alpha ^2}-\frac{40a}{\alpha } \right) }\left( erf \left( \frac{a}{b}\right. \right. \\&\left. \left. \left. -\frac{10\alpha log \frac{(i-1)\varepsilon }{c}}{b}-\frac{b}{20\alpha }\right) - erf\left( \frac{a}{b}-\frac{10\alpha log \frac{i\varepsilon }{c}}{b}-\frac{b}{20\alpha }\right) \right) \right] \end{aligned} \end{aligned}$$

(41)

1.2 Appendix 3

Derivation of  (28):

The integral in (28) can be written as

$$\begin{aligned} \begin{aligned} \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon }P(\gamma _b(x)\succeq \psi ) dx = \frac{1}{\varepsilon } \left[ \int \limits _{0}^{i\varepsilon }e^{\frac{-\psi x^\alpha P_{noise}}{kP_t}} dx - \int \limits _{0}^{(i-1)\varepsilon }e^{\frac{-\psi x^\alpha P_{noise}}{kP_t}} dx \right] \\ \end{aligned} \end{aligned}$$

(42)

Substituting $\frac{\psi x^\alpha P_{noise}}{kP_T}=t$ the above integral can be written as

$$\begin{aligned} \begin{aligned} \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon }P(\gamma _b(x)\succeq \psi ) dx =&\frac{1}{\varepsilon \alpha } \left( \frac{\psi P_{noise}}{kP_t}\right) ^{(-1/\alpha )} \left[ \int \limits _{0}^{\frac{\psi (i \varepsilon )^\alpha P_{noise}}{kP_t}}e^{-t}\,t^{(1/\alpha -1)} dt\right. \\&\left. - \int \limits _{0}^{\frac{\psi ((i-1) \varepsilon )^\alpha P_{noise}}{kP_t}}e^{-t}\,t^{(1/\alpha -1)} dt \right] \\ \end{aligned} \end{aligned}$$

(43)

The above integral can be simplified to get the following expression for $E[P(\gamma _b(i)\succeq \psi )]$

$$\begin{aligned} \begin{aligned} E[P(\gamma _b(i)\succeq \psi )]&= \frac{1}{\varepsilon \alpha } \left( \frac{\psi P_{noise}}{kP_t}\right) ^\frac{-1}{\alpha } \left[ \gamma \left( \frac{1}{\alpha },\frac{\psi P_{noise}(i\epsilon )^\alpha }{kP_t}\right) - \gamma \left( \frac{1}{\alpha },\frac{\psi P_{noise}((i-1)\epsilon )^\alpha }{kP_t}\right) \right] \end{aligned} \end{aligned}$$

(44)

where $\gamma (s,t)$ is the lower incomplete gamma function [32].

1.3 Appendix 4

Derivation of (33):

Consider the integral expression in (33).

$$\begin{aligned} \begin{aligned} \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon } P(\gamma _b(x) \succeq \psi ) dx&= \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon } e^{\frac{-(K+1)\psi d^\alpha P_{noise}}{k P_t}} e^{-K} \sum \limits _{t=0}^{\infty } \frac{K^t}{t!} \sum \limits _{l=0}^{t}\left( \frac{(K+1)\psi d^\alpha P_{noise}}{k P_t}\right) ^l \frac{1}{l!} \\ \end{aligned} \end{aligned}$$

(45)

substituting $c=\frac{(K+1)\psi P_{noise}}{kP_t}$ and by using the definite integral rules (45) can be written as

$$\begin{aligned} \begin{aligned} \frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon } P(\gamma _b(x) \succeq \psi ) dx&\,=\, \frac{1}{\varepsilon } e^{-K} \sum \limits _{t=0}^{\infty } \frac{K^t}{t!} \sum \limits _{l=0}^{t} \frac{c^l}{l!} \left[ \int \limits _{0}^{i\varepsilon } x^{\alpha l}e^{-cx^\alpha } dx - \int \limits _{0}^{(i-1)\varepsilon } x^{\alpha l}e^{-cx^\alpha } dx \right] \\ \end{aligned} \end{aligned}$$

(46)

The above integral can be simplified to get the following expression for $E[P(\gamma _b(i)\succeq \psi )]$ [32]

$$\begin{aligned} \begin{aligned} E[P(\gamma _b(i) \succeq \psi )] =\, &\frac{1}{\varepsilon } \int \limits _{(i-1)\varepsilon }^{i\varepsilon } P(\gamma _b(x) \succeq \psi ) dx \\ =\,&\frac{1}{\varepsilon } \left( \frac{(K+1)\psi P_{noise}}{k P_t}\right) ^{-1/\alpha } e^{-K} \sum \limits _{t=0}^{\infty } \frac{K^t}{t!} \\&\times \sum \limits _{l=0}^{t}\frac{1}{l!} \left[ \gamma \left( l+\frac{1}{\alpha }, \frac{(K+1)\psi P_{noise}}{k P_t}\right) (i\varepsilon )^\alpha \right. \\&\left. - \,\gamma \left( l+\frac{1}{\alpha }, \frac{(K+1)\psi P_{noise}}{k P_t}\right) ((i-1)\varepsilon )^\alpha )\right] \end{aligned} \end{aligned}$$

(47)

where $\gamma (s,t)$ is the lower incomplete gamma function [32].