Discover hidden web properties by random walk on bipartite graph

Abstract

This paper proposes to use random walk (RW) to discover the properties of the deep web data sources that are hidden behind searchable interfaces. The properties, such as the average degree and population size of both documents and terms, are of interests to general public, and find their applications in business intelligence, data integration and deep web crawling. We show that simple RW can outperform the uniform random (UR) samples disregarding the high cost of UR sampling. We prove that in the idealized case when the degrees follow Zipf’s law, the sample size of UR sampling needs to grow in the order of O(N/ln ² N) with the corpus size N, while the sample size of RW sampling grows logarithmically. Reuters corpus is used to demonstrate that the term degrees resemble power law distribution, thus RW is better than UR sampling. On the other hand, document degrees have lognormal distribution and exhibit a smaller variance, therefore UR sampling is slightly better.

1 Introduction

Searchable forms are ubiquitous on the web. Many web sites, especially the large ones, have searchable interfaces such as HTML Forms or programmable web APIs. The data hidden behind a searchable interface constitute a hidden web data source (Bergman 2001) that can be accessed by queries only. The profiles of a hidden data source, including the average degrees and the total population size for both terms and documents in a data source, are of great interest to general public and business competitors (Lawrence and Giles 1998), to data crawlers (Ipeirotis et al. 2001; Lu et al. 2008; Madhavan et al. 2008; Raghavan and Garcia-Molina 2001; Wang et al. 2012), and to virtual data integrators such as vertical portals and meta search engines (Shokouhi and Si 2011; Si et al. 2002). In business intelligence, people would like to know the number of users in Facebook, their average number of follower and their variations. In distributed information retrieval there is a need to profile the data sources before deciding where the queries should be sent to (Callan and Connell 2001; Shokouhi and Si 2011). In deep web crawling, it needs to know how many documents are there so that it can decide when to stop the crawling (Madhavan et al. 2008; Wu et al. 2006).

Discovering these properties has been a long lasting challenge (Callan and Connell 2001), mainly due to the unequal probability of the data being sampled, or the heterogeneity of the data. Consequently it is difficulty or costly to obtain the uniform random (UR) samples (Bar-Yossef and Gurevich 2006; Bar-Yossef and Gurevich 2011). This paper shows that instead of using UR samples, the biased sample obtained by simple random walk (RW) on the document-term graph can perform better.

For instance, we may want to learn the average document frequencies of the terms in a data source, or the average degree of the terms in its term-document graph. Average degree can be used to derive other properties such as degree variance and population size as we will show in Sect. 4. In turn average degree and population size reveal the total number of terms of the hidden corpus.

Given N number of terms labeled as $1, 2, \ldots, N$, and their degrees $d_1, d_2, \dots, d_N$. The average degree is

$$\langle d \rangle=\frac{1}{N}\sum_{i=1}^{N} d_{i}.$$

(1)

One obvious but often impractical estimation method is via UR sampling, i.e., select a set of terms $\{ x_1, x_2 \ldots, x_n\}$ where $x_i \in \{1, 2, \ldots, N\}$ randomly with equal probability, count their degrees $\{d_{x_1}, d_{x_2}, \ldots\, d_{x_n}\}$ for each term, and calculate the sample mean as the estimate of the population mean:

$$\widehat{\langle d \rangle}_{SM}=\frac{1}{n}\sum_{i=1}^{n} d_{x_i}.$$

(2)

The sample mean estimator $\widehat{\langle d \rangle}_{SM}$ is unbiased if the terms or documents are homogeneous, i.e., they can be selected randomly with equal probability. Unfortunately this is not the case in most practice. Popular terms have a higher probability being sampled if terms are selected randomly from a document. Similarly, large documents tend to have a higher probability of being sampled if they are selected by random queries.

To analyze such heterogeneous data where elements have unequal probabilities of being sampled, various sampling methods have been studied for hidden data sources including search engine indexes (Bar-Yossef and Gurevich 2006), and in related areas such as the Web (Henzinger et al. 2000), graphs (Bar-Yossef and Gurevich 2008; Leskovec and Faloutsos 2006), online social networks (Gjoka et al. 2009; Papagelis et al. 2011), and real social networks (Salganik and Heckathorn 2004; Wejnert and Heckathorn 2008). The typical underlying techniques include Metropolis Hasting Random Walk (MHRW) (Metropolis et al. 1953) for uniform sampling and RW (Lovász 1993) for unequal probability sampling. MHRW is reported rather good at obtaining a random sample. However, in the sampling process many nodes are retrieved, examined, and rejected. The cost is rather high especially for hidden data sources. The samples are retrieved by queries that occupy network traffic, let alone the daily quotas impose by data providers. Thus a practical sampling method should include all the samples even if they induce bias.

Even when random samples are obtained, the sample mean estimator has a high variance because the degree distribution of the terms usually follows Zipf’s law (Montemurro 2001; Zipf 1949). Most terms have small degrees, while a few of them have huge degrees. The inclusion/exclusion of a huge term such as a stop word in a sample will make the estimation diverge.

We propose to use harmonic mean, instead of arithmetic mean, of the sample as the estimator of the average degree of documents and terms:

$$\widehat{\langle d \rangle}_H=n \left[\sum_{i=1}^{n} \frac{1}{d_{x_i}} \right]^{-1}.$$

(3)

Here the subscript H indicates that it is the harmonic mean, and that it can be derived from the traditional Hansen–Hurwitz estimator (Hansen and Hurwitz 1943).

The sample for this estimator is obtained by low cost simple RW where the node selection probability is asymptotically proportional to its degree. It is rather common to use Hansen–Hurwitz related estimators when selection probabilities are not equal for elements in the population. But usually people use probability proportional to size (PPS) sampling because of the unavailability of random samples (Salganik and Heckathorn 2004). This paper shows that $\widehat{\langle d \rangle}_H$ can be better than the sample mean estimator even when UR samples are available—it has a very small bias, and the variance is smaller than the sample mean estimator for terms and is only slightly larger for the documents.

The crux of population size estimation is the heterogeneity of the data–documents and terms have unequal probabilities of being sampled. Yet the degree of the heterogeneity, called coefficient of variation (CV, denoted as γ hereafter), is difficult to predict in traditional sampling studies where the accurate degree is hard to quantify. In our setting the degrees of sampled documents and terms are easy to obtain, thereby the average degree is ascertained accurately thanks to the estimator $\widehat{\langle d \rangle}_H$. Thus, the CV can be estimated by

$$\widehat{\gamma}^2+1=\frac{1}{\langle d \rangle n}\sum_{1}^{n} d_{x_i}.$$

(4)

With the knowledge of γ, the population size can be obtained by

$$\widehat{N}=(\widehat{\gamma}^2+1)N_0=(\widehat{\gamma}^2+1)\left(\begin{array}{l} n \\ 2 \end{array}\right)\frac{1}{C}.$$

(5)

Here N ₀ is an estimator for homogeneous data, and $\left(\begin{array}{l} n \\ 2 \end{array}\right)\frac{1}{C}$ is one of the N ₀ estimators. C is the collisions of the nodes happened during sampling.

Our main contributions in this paper can be summarized as follows:

• For average degree estimation we show that RW sampling can outperform UR sampling, even ignoring the high cost of obtaining the UR samples.

• We show that RW is not always better than UR sampling. We give the condition when RW could be better.

• We show that average degree is an important property that can lead to the discovery of the population size;

• We solved the open problem to correct the bias in capture–recapture method. It is well known in the area of capture–recapture method that there is a negative bias when the data is heterogeneous. The problem to quantify and consequently correct this bias has never been solved. We show that the population size can be estimated first as if the data were homogeneous, then multiply the estimation by γ² + 1. In particular, we show that it is a practical approach because of the success estimation of the mean degree that leads to the discovery of γ².

In the following we will first introduce the related work, especially the background of population size estimation. Then we model the query-based sampling as a RW on a bipartite graph. Section 4 introduces two estimators, one for average degree and the other for population size. We prove that in the idealized case where term degrees follow Zipf’s law with exponent one, our proposed estimator $\widehat{\langle d \rangle}_H$ is much better than $\widehat{\langle d \rangle}_{SM}$ when the corpus size is large. The experiments section dissects the Reuter corpus with details of the data distributions, sample distributions, and estimation results with various sample sizes. Then we give an intuitive explanation for why $\widehat{\langle d \rangle}_H$ can reduce the variance.

2 Related work

Query based profiling of hidden data sources has been studied ever since the occurrence of web query interfaces. One of the early influential works is the estimation of search engine size (Lawrence and Giles 1998). The problem can be further classified by the syntax of the queries allowed and the types of data bases sitting behind. Queries can be simple key words (Broder 2006; Callan et al. 1999; Lu and Li 2010; Shokouhi et al. 2006; Zhang et al. 2011), boolean expressions (Lawrence and Giles 1998), or even SQL queries (Dasgupta et al. 2007, 2010; Haas et al. 1995). The data sources can be text databases such as a collection of documents (Bar-Yossef and Gurevich 2008; Callan et al. 1999; Broder 2006; Shokouhi et al. 2006), or structured data in the form of relational database tables (Dasgupta et al. 2007; Dasgupta et al. 2010; Haas et al. 1995). Our paper assumes simple keyword interfacing with textual database.

The background of this research is the population size estimation and sampling that have been widely studied in other disciplines (Thompson 2012) especially in ecology (Amstrup et al. 2005) and social studies (Salganik and Heckathorn 2004), and more recently in computer science for estimating the size of the web (Lawrence and Giles 1998), databases (Haas et al. 1995), web data sources (Broder 2006; Dasgupta et al. 2010; Henzinger et al. 2000; Zhang et al. 2011; Zhou et al. 2011), and online social networks (Gjoka et al. 2009; Katzir et al. 2011; Ye and Wu 2011).

2.1 Average degree estimation

At the first sight, the average degree estimation problem seems neither important nor difficult. In reality it is an important problem in that (1) it leads to the discovery of the CV, in turn CV can be used in the population size estimation; (2) it reveals the overall data size. Average degree estimation is also a difficult problem because UR samples may not be directly available due to the restricted sampling interface as in the query-based sampling. Although there are studies to obtain the UR sample using rejection method or MHRW (Bar-Yossef and Gurevich 2008), the cost will be rather high. Therefore there are studies to use the biased sample directly, and use harmonic mean to adjust the bias. The detailed derivation of the harmonic mean estimator can be found in (Salganik and Heckathorn 2004) where the purpose is to sample hidden population such as drug-addicts. In this setting it is impossible to evaluate the estimator because neither the true value nor the sampling probability can be verified. The biased samples are taken because UR sampling is impossible. The harmonic mean estimator is derived to correct the bias, not to improve the performance of the estimation.

In the area of peer-to-peer network (Rasti et al. 2009) and online social network (Gjoka et al. 2011; Kurant et al. 2011), the re-weighted RW that resembles harmonic mean was used and empirically compared with MHRW, but not with UR samples.

Our work is the first to show that RW can outperform UR samples disregarding the cost of obtaining these samples. In addition, we give the conditions when RW could be better. The preliminary result was also published in our workshop paper (Lu and Li 2012) where the data is online social network. This paper reports our recent progresses on the following aspects: (1) we experiment on text bipartite graph instead of the non-bipartite graph representing social networks; (2) we show that RW is not always better than UR sampling, and analytically give the conditions when RW outperforms UR sampling; (3) the experiments verify that when the degree distribution follows power law, RW sampling is much better than UR sampling. When the degree distribution is log-normal, UR is slightly better than RW sampling; (4) in addition to average degree estimation, population size estimation is discussed and experimented in detail; (5) we add the intuitive explanation as for why UR can be better than RW sampling.

2.2 Population size estimation

2.2.1 Capture–recapture method

The starting point of population estimation is the well-known Lincoln–Petersen estimator (Amstrup et al. 2005) that can be applied when there are two sampling occasions and every node has equal probability of being sampled:

$$\hat{N}_{LP}=\frac{n_1n_2}{d},$$

(6)

where n ₁ is the number of nodes sampled in the first capture occasion, n ₂ is the number of nodes sampled in the second occasion, d is the duplicates among two samples. The assumptions of Lincoln–Petersen estimator can be hardly met in reality. It is extended in two dimensions: one is allowing multiple sampling occasions, the other is supporting heterogeneity in capture probability, as will be discussed in the next two subsections.

Albeit its simplicity and severe restriction, most of the existing work used the capture–recapture sampling method and the corresponding Lincoln–Petersen estimator in one form or another. The classic work is the estimation of the Web and the search engines described in (Lawrence and Giles 1998) and (Bharat and Broder 1998). Both approaches use queries to capture documents, and count the duplicates between the two captures. In (Lawrence and Giles 1998), Lawrence and Giles were aware that the estimation is not accurate, therefore they presented the estimation as relative size, not the absolute size. Bharat and Broder (1998) investigated the causes for the inaccuracy, in particular the unequal probability of documents being matched by queries (called query bias in their paper). They proposed to alleviate the bias by obtaining UR samples, say, from the search engine directly as privileged users instead of public searchable interfaces. Gulli and Signorini (2005) used the same method in a larger scale, by building query lexicon from dmoz.com directory that contains 4 million pages.

Continuing in this direction, other innovative methods are proposed for those two captures, not necessarily by two queries. Nonetheless, the underlying estimator is still Lincoln–Petersen estimator, and the bias problem remains un-tackled. Both Si et al. (2002) and Kunder ¹ used query frequencies to estimate search engine sizes. They take a sample set of documents with size (n ₁), and another sample set of documents that contain a specific query. Say the second capture is of size n ₂, which is actually the document frequency of the query, and it may be provided by search engines. The overlapping d is the the intersection of those two sets, i.e., the number of documents that match the query in the sample documents. The advantage of this method is that n ₂ does not need to be calculated by the sampler. The disadvantage is also obvious: in both sampling occasions the documents are not sampled with equal probability. What is worse, the document frequency returned by search engines are often inflated, sometimes in orders of magnitude.

In Broder et al. (2006) also use Lincoln–Petersen estimator, but each capture is defined as the documents covered by many queries. Because the number of queries is very large, it is not possible to obtain n ₁ and n ₂ directly by actually submitting the queries. Instead n ₁ and n ₂ themselves are estimated.

Equation 6 is ubiquitous and applied in various forms. Quite often even the users may not be aware that they are actually applying the basic capture–recapture method. For instance, ID sampling is used to estimate Facebook population by leveraging the fact that each ID is a 9-digit number (Gjoka et al. 2009). The estimation method is to select a number uniformly at random in the range 1–10⁹, then probe the server to check whether it is a valid ID. Suppose that the total number of valid IDs is n ₁, the probings being sent is n ₂, and valid ones among the samples are the duplicates between the two sets, denoted as d. Then, according to 6, we have 10⁹ = n ₁ n ₂/d. When n ₂ and d are available, we can use the equation to estimate n ₁, the number of valid IDs.

2.2.2 Multiple capture–recapture method

When there are more than two sampling occasions and each time only one sample is taken, Darroch (1958) derived that the approximate Maximum Likelihood Estimator (MLE), $\widehat{N}_{D}$, is the solution of the following equation:

$$n-d=N\left(1-e^{-\frac{n}{N}}\right),$$

(7)

where n is the total sample size, and d is the duplications. This equation has also been used to predict the isolated nodes in random graph when edges are randomly added (Newman 2010). Unfortunately it does not have a simple closed form solution (Darroch 1958; Newman 2010), i.e., it can not be solved algebraically for N. In online social network studies, Ye and Wu (2011) used numeric method to find the solution to this estimator. Lu and Li (2010) gives an approximate solution for N that reveals a power law governing the data not sampled and the overlapping rate. In a simpler form, it states that the percentage P of the data not sampled decreases in the power of the overlapping rate R = n/(n − d), i.e.,

$$P=R^{-2.1}.$$

(8)

2.2.3 Unequal sampling probability

When the data is heterogeneous, i.e., elements have unequal probabilities of being sampled, the estimation becomes notoriously difficult. One approach to solving this problem is to obtain the UR sample (Bar-Yossef and Gurevich 2008) using algorithms such as MHRW, then traditional estimators are applied on the random sample. The other approach uses the biased sample to save the sampling cost, but adjust the bias by devising new estimators (Broder et al. 2006; Lu and Li 2010; Shokouhi et al. 2006). Broder et al. (2006) assigned less weight to long documents being sampled; Shokouhi et al. (2006) run regression on past data to establish the relationship between the homogeneous and heterogeneous data; Lu (2008) and Lu and Li (2010, 2013) went a step further by using γ, the degree of heterogeneity, to adjust the discrepancy.

The problem is that estimating γ itself is equally challenging. Therefore Eq. 5 as an estimator for N was not seen in ecology. Instead, the same equation was used by Chao et al. (1992) in a reverse way to estimate γ as below:

$$\widehat{\gamma^2}= N_{0}C{\left(\begin{array}{l} n \\ 2 \end{array}\right)}^{-1}-1,$$

(9)

where N ₀ is a rough estimation for N assuming the data is homogeneous. This method was demonstrated (Chao et al. 1992) on small data where γ² is typically around one. That is, the ratio between N and N ₀ is around two. In our large and power law data γ² can go up to hundreds, making the traditional estimator biased downwards by hundreds of times smaller than the real value.

In the estimation of digitalized networks such as hidden web data sources, the sampling probability for each node can be (partially) decided by the degrees. Unlike traditional sampling schemes where sampling probability of animals are different but the exact variance is impossible to quantify accurately, in the simple RW on the term-document graph we know not only the exact degree of the node being visited, but also that the sampling probability is proportional to its degree. With this knowledge, we can obtain the value of γ, thereby estimator $\widehat{N}$ can be applied. Not surprisingly, Katzir et al. (2011) used a similar equation to estimate the size of online social networks:

$$\widehat{N_K}=\frac{1}{2C} \sum_{1}^{n} d_{x_i} \sum_{1}^{n} 1/d_{x_i},$$

(10)

which can be transformed to estimator $\widehat{N}$. Katzir et al. (2011) showed that it is a consistent estimator.

Note that estimator $\widehat{N}$ can be approximated by equations either 7 or 8 when γ = 0, sample size is small, and collisions C can be approximated by duplicates d. The approximation can be established by applying Taylor expansion on the right hand side of Eq. 7.

2.3 Other size estimation methods

In contrast to the traditional sampling in ecology and social studies, the diversity of the access interfaces to web data collections opens up opportunities for designing sampling schemes that take advantages of interface specifics. For instance, Gjoka et al. (2009) samples valid Facebook IDs from an ID space of 9 digits, utilizing the Facebook implementation details that make the number of invalid IDs not much bigger than the valid ones; Zhou et al. (2011) leverages the prefix encoding of Youtube links; Dasgupta et al. (2010) depends on the negation of queries to break down the search results; Lu (2010) and Zhang et al. (2011) deals with the return limit of the search engines. Dasgupta et al. (2007, 2010) use RW in query space to probe database properties, which is different from our RW in that (1) they suppose the SQL like syntax of the queries that support boolean expressions. (2) The RW is on the query space constructed by the boolean operators, not the document-term graphs in our paper.

3 Problem definition

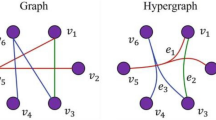
Following (Olston and Najork 2010; Wu et al. 2006; Zhang et al. 2011), a hidden data source can be modelled as a document-term bipartite graph G = (D, T, E), where nodes are divided into two separate sets, D the set of documents, and T the set of terms. Every edge in E links a term and a document. There is an edge between a term and a document if the term occurs in the document.

Let d ^D _i denote the degree of the document node i, for $i \in \{1, 2, \ldots, |D|\}$, i.e., the number of distinct terms in document i. Let d ^T _j denote the degree (or document frequency) of the term node j for $j \in \{1, 2, \ldots, |T|\}$. The volume τ of the documents D (or the volume of terms T) is

$$\tau=\displaystyle\sum_{i=1}^{|D|} d_i^D=\sum_{j=1}^{|T|} d_j^{T}.$$

The mean degree of documents D is $\langle d^D\rangle=\tau/ |D|$, and the mean degree of terms T is $\langle d^T \rangle=\tau/|T|$.

The goal of this paper is to estimate $\langle d^D\rangle, \langle d^T\rangle, |D|$ and |T| using a sample. When it is clear from the context, we will omit the superscript D and T, using $\langle d \rangle$ to denote the average degree for documents or terms, and N to denote the size of the population |D| or |T|. We use terms and queries interchangeably with slight different connotations: a lexeme in a document is a term. When a term is sent to a searchable interface it is called a query.

Example 1

(Bipartite graph of hidden web) Figure 1 gives an example of a hidden data source that is represented as a bipartite graph, where $D=\{d_1, d_2, \ldots, d_9\}$ and $T=\{q_1, q_2, \ldots, q_7\}.\,\langle d^T\rangle= 18/7$, and $\langle d^D \rangle =18/9.$

Fig. 1

Hidden data source as a bipartite graph a bipartite graph, b same graph as (a) in spring model layout

A simple RW on the document-term graph is described in Algorithm 1. First a seed query is selected randomly from a dictionary and the list of the matched document URLs are retrieved. From the list we select randomly one of the URLs and download the corresponding document. From the downloaded document a query is selected randomly and sent to the data source. The process is repeated until n number of sample documents and n number of sample terms are obtained. In the samples the documents or the terms can be visited multiple times. In other words it is a sampling with replacement.

During the RW process, we do not need to explore all matched documents. Instead, we can first ask for the number of matches m, generate a random number r between 1 and m, then directly access the page containing the r-th document. Therefore for each sample document and term at most two queries are needed, one to get the degree of the query, the other to get the page containing the rth document.

Example 2

(Random walk) If the sample size n is 5 and the seed term is q ₁. A RW result can be

$$\begin{aligned} T_s&=((q_1, 1), (q_6,5), (q_7,5), (q_7,5), (q_6,5))\\ D_s&=((d_2, 3), (d_4,2), (d_1,1), (d_7,3), (d_3,2)) \end{aligned}$$

4 Estimators

This paper focuses on two properties, the average degree and the total population size for both terms and documents. When UR samples are available, the former property can be estimated by the sample mean, the latter by capture–recapture methods (Amstrup et al. 2005). However, UR samples are not easy to obtain. It is well known that in RW large documents and queries have higher probability of being visited. Asymptotically the sampling probability of a document or a term is proportional to its degree. Therefore we need to use estimators developed for such samples whose sampling probability is proportional to their sizes.

We first develop the estimation of average degree, including the average length (number of distinct terms) of the documents and the average size (or document frequency) of terms. Based on the average degree, the estimator of population size (total number of terms and documents) is derived.

Table 1 summarizes the notations used in this paper.

Table 1 Summary of notations

4.1 Average degree

Suppose that in the document-term graph there are N number of document nodes. Node i has a degree $d_i, i \in \{1, 2, \ldots, N\}$. Let the total number of document degree is τ = ∑ ^N _i=1 d _i , and the mean of document degrees is $\langle d \rangle=\tau/N$.

The variance σ² of the degrees in the population is defined as (Thompson 2012)

$$\sigma^2= \langle d^2 \rangle-\langle d \rangle^2,$$

(11)

where $\langle d^2 \rangle$ is the arithmetic mean of the square of the degrees in the total population.

The coefficient of variation (CV, also denoted as γ) is defined as the standard deviation, or the square root of the variance, normalized by the mean of the degrees:

$$\gamma^2=\frac{\sigma^2}{\langle d \rangle^2}=\frac{\langle d^2 \rangle}{\langle d \rangle^2}-1.$$

(12)

A sample of n elements $(d_{x_1}, \ldots, d_{x_n})$ is taken from the population, where $x_i \in \{1,2 ,\ldots, N\}$ for $i=1, 2, \ldots, n$. Our task is to estimate the average degree $\langle d \rangle$ using the sample.

4.1.1 Sample mean estimator

If a UR sample $(d_{x_1}, \ldots, d_{x_n})$ is obtained, the sample mean is an unbiased estimator as defined below:

$$\widehat{\langle d \rangle}_{SM}= \frac{1}{n}\sum_{i=1}^{n} d_{x_i}.$$

(13)

The variance of the estimator $\widehat{\langle d \rangle}_{SM}$ is (Thompson 2012)

$$var(\widehat{\langle d \rangle}_{SM})= \frac{\sigma^2}{n}.$$

(14)

The problem with this sample mean estimator is that the UR sample is not easy to obtain. Moreover, its variance is too large to be of practical application if the degrees have a large variance. It is well established that the degree of the terms follows Zipf’s law, causing the population variance σ² of the term degrees very large.

More specifically, if the degrees follow the Zipf’s law strictly, the variance of the sample mean estimator can be described by the following theorem

Theorem 1

Suppose the degrees follow Zipf’s law with exponent one, i.e., $d_i=\frac{A}{\alpha+i}$, where A and α are constants. The variance of the sample mean estimator is

$$var(\widehat{\langle d \rangle}_{SM}) \approx \frac{\langle d \rangle^2}{n}\left(N \left[ \alpha \ln^2 \frac{N+\alpha}{1+\alpha} \right ]^{-1}-1\right).$$

(15)

Proof

See “Appendix”.

4.1.2 Harmonic mean estimator

When sampling probability is not equal for each unit, a common approach is to use Hansen–Hurwitz estimators (Thompson 2012). In the case where the sampling probability of a node is proportional to its degree, the estimator for degree mean $\widehat{\langle d \rangle}_H$ is the harmonic mean of the degrees:

$$\widehat{\langle d \rangle}_H =n \left[ \sum_{i=1}^{n} \frac{1}{d_{x_i}}\right]^{-1}.$$

(16)

We refer to Salganik and Heckathorn (2004) for detailed derivations of the estimator in the setting of respondent driven sampling. Also it can be derived as a special case of importance sampling (Liu 2008). Unlike the unbiased estimator $\widehat{\langle d \rangle}_{SM}$, $\widehat{\langle d \rangle}_H$ is biased. According to Cochran (1977) the bias is on the order of 1/n. Since the sample size n in our setting is far greater than one in general, the bias is negligible. Its variance can be derived from the variance of Hansen–Hurwitz estimator using the Delta method, resulting in:

$$\widehat{var}(\widehat{\langle d \rangle}_H)=\frac{s_v^2}{\overline{v}^4n},$$

(17)

where $v_i=1/d_{xi},\,\overline{v}$ and s ² _v are the sample mean and variance of v _i ’s. This estimated variance will be supported by our experiments in Sect. 5.

In the idealized case when the degrees follows exactly with Zipf’s law, we have the following theorem that can highlight the reduced variance of the estimator:

Theorem 2

When the degrees follow Zipf’s law whose exponent is one, the variance of the estimator is

$$var(\widehat{\langle d \rangle}_H)=\frac{\langle d \rangle^2}{n} \left( \frac{1}{2}\ln \frac{N+\alpha}{1+\alpha}-1\right).$$

(18)

Proof

See “Appendix”.

Comparing the variances of estimators $\widehat{\langle d \rangle}_{SM}$ and $\widehat{\langle d \rangle}_H$, we can see that the variance of $\widehat{\langle d \rangle}_H$ grows logarithmically with corpus size N, while $\widehat{\langle d \rangle}_{SM}$ increases in the order of O(N/ln ² N), almost linearly with N when N is large. In other words, in order to make the variance commensurate to the real value $\langle d \rangle^2$, the sample size n should be in the order of N for $\widehat{\langle d \rangle}_{SM}$, but merely $\ln \, N$ for $\widehat{\langle d \rangle}_H$.

Example 3

(Degree estimation) For our example, the harmonic mean estimation for average degree of terms is

$$\widehat{\langle d \rangle}_H=\frac{n}{\sum 1/d_i} = \frac{5}{\frac{1}{1}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}}=\frac{25}{9}=2.7778.$$

For documents the estimated average degree is

$$\widehat{\langle d \rangle}_H=\frac{n}{\sum 1/d_i} = \frac{5}{\frac{1}{3}+\frac{1}{2}+\frac{1}{1}+\frac{1}{3}+\frac{1}{2}}=\frac{30}{16}=1.875.$$

4.2 Population size estimation

The population size can be estimated as follows,

$$\widehat{N}= (\gamma^2+1)\widehat{N_0}=(\gamma^2+1){\left(\begin{array}{l} n \\ 2 \end{array}\right)} \frac{1}{C},$$

(19)

where $\widehat{N_0}$ is the estimation of N if the samples are taken uniform randomly, n is the sample size, C is the number of collisions, γ is CV of the degrees. Let f _i denote the number of individuals that are visited exactly i times.

$$C=\sum_{i=1}^{+\infty}{\left(\begin{array}{l} i \\ 2 \end{array}\right)}f_i.$$

The derivation of the estimator is given in Appendix 9.3. It can be also derived as a special case of Eq 3.20 in (Chao et al. 1992). But that equation is used to estimate γ instead of N. Katzir et al. (2011) used an equivalent formula but in a very different form.

Note that this is a biased estimator as we pointed out in (Lu and Li 2013). The relative bias is approximately 1/C, and can be corrected using the following estimator. When collisions C is large, such bias can be neglected. This paper uses the estimator in Eq. 19 to focus on the other bigger bias, i.e., the bias introduced by γ.

$$\widehat{N}^*= (\gamma^2+1){\left(\begin{array}{l} n \\ 2 \end{array}\right)} \frac{1}{C+1},$$

(20)

The elegance of the equation is that when the samples are uniform, γ = 0, and the estimator is reduced to the traditional birthday paradox or capture–recapture method. When the sample is obtained by RW, the sampling probability is not equal among all the documents or terms, resulting in γ > 0. The population size can be estimated as if the samples were taken uniformly, then multiplied by γ² + 1. This was not seen in literature as far as we are aware.

The reason of this formulation being overlooked may due to the challenge of determining γ in traditional estimation problems. In ecology and social studies the degree of a node can not be quantified accurately. For instance, it is hard to determine the friends of a drug-addict. This makes it impossible to perform a simple RW in the graph. In our setting of deep web data sources, we know exactly the number of documents a query matches, and the number of terms a document contains. Leveraging this information, the heterogeneity γ of the data can be obtained by simple RW as below. Asymptotically the mean of the degrees obtained by a RW is

$$\langle d^w \rangle =\sum_{i=1}^{N} p_id_i =\frac{\langle d^2 \rangle}{\langle d \rangle},$$

(21)

where p _i  = d _i /τ is the selection probability of node i. Hence

$$\gamma^2+1=\frac{\langle d^w \rangle}{\langle d \rangle},$$

(22)

where $\langle d^w \rangle$ can be estimated by its sample mean

$$\widehat{\langle d^w \rangle}=\frac{1}{n} \sum_{i=1}^{n} d_{x_i},$$

(23)

and $\langle d\rangle$ can be estimated by its harmonic mean ${\langle\widehat{d}\rangle}_H$. Combining the two equations we derive the estimator for γ as follows:

$$\widehat{\gamma}^2+1=\frac{\widehat{\langle d^w \rangle}}{\widehat{\langle d \rangle}}=\frac{1}{n^2} \sum_{1}^{n} d_{x_i}\sum_{1}^{n} 1/d_{x_i}.$$

(24)

The convenience of the method is that only one RW is needed to obtain both $\widehat{\langle d \rangle}$ and $\widehat{\langle d^w \rangle}$.

Example 4

(Population size estimation) Continuing on our example data source for terms.

$$\widehat{\gamma^2}+1 =\frac{\widehat{\langle d^w \rangle}}{\widehat{\langle d\rangle}} = \frac{21/5}{25/9}=1.512.$$

n = 5, f ₁ = 1 (q ₁), f ₂ = 2 (q ₆ and  q ₇), therefore

$$\begin{aligned} C &=\sum_{i=1}^{\infty} {\left(\begin{array}{l} i \\ 2 \end{array}\right)} f_i =2, \\ \widehat{N}&=1.512 \times \frac{4\times 5}{2} \times \frac{1}{2}=7.56. \end{aligned}$$

5 Experiments

5.1 Datasets

Our method is tested against several datasets including Reuters newswires (Reuters 2008) (Reuters), newsgroups ² (NG20), KDDCUP 2013 research papers (KDDCUP), ³ and a subset of Wikipedia (Wiki). The statistics of these datasets are summarized in Table 2. In this experiment a term is a sequence of letters and is case-insensitive. The term population N is the total number of distinct terms that are collected in all the documents in the corpus. The degree of a term is the document frequency of the term, i.e., the number of documents that contain the term. The degree of a document is the number of distinct terms in that document.

Table 2 Summary of the datasets

Table 3 Relative standard errors of the estimations

We list γ, the normalized standard deviation of the degrees, for each dataset. It is well known that term degrees (document frequencies) follow power law, while document degrees follow lognormal law. Reflected in our datasets, γ for term degree is larger than that of the document degrees. As a verification, we show distributions of Reuters, for both term degrees and document degrees in Fig. 2. In order to show both ends of the distributions, we plot the degree against its rank in sub panel (A) and (C), as well as the frequency against its degree in sub panels (B) and (D). The former plot has a better view of the top degrees, while the latter depicts better the small terms or documents. Clearly the distributions of term degrees and document degrees are different, which is the cause of different values for γ, and different results on average degree estimation for terms and documents. The term degrees obviously follow Zipf’s law, while document degrees are more like log-normal distribution. In addition, document degrees sit in a very narrow range (min is 6, max is 1,659) compared with term degrees (1–434,202). Therefore the heterogeneity of those two kinds of degrees are very different. CV of term degrees is 16, and CV of document degree is merely 0.7.

Fig. 2

Degree distribution of terms (a, b) and documents (c, d) in Reuters corpus. a and c are degree versus rank plots. b and d are frequency vs. degree plots. It shows that terms have a larger variance than documents

5.2 Summary of the results

First, we evaluate the estimators in terms of relative standard error (RSE) that is defined as below:

$$RSE(\hat{d})=\frac{1}{{\mathbb{E}}(\hat{d})}\left[{\mathbb{E}} (\hat{d}-{\mathbb{E}}(\hat{d}))^2 \right]^{1/2},$$

(25)

where ${\mathbb{E}(X)}$ is the expectation of X, i.e., the mean of all the possible values, which can be approximated by the sample mean when the number of values is large. We omit bias or MSE because these estimators have negligible biases when the sample size is not small, and the degree estimator for UR sampling does not have bias. In the next subsection, we will give more detailed evaluation for Reuters data in terms of both bias and variance.

Table 3 summarizes the RSEs for the four combinations of two estimators for both terms and documents. For average degree estimation, the sample size is 200 (5,000 for Reuters). RSE is obtained from 2,000 repetitions (200 for Reuters). For population size estimation, the sample size varies with real data size N, approximately in the order of $\sqrt{2N}$. That is the number needed to produce some collisions.

Overall, we observe that RW outperforms UR samples, by obtaining smaller variance using the same sample size. There are also cases where RW is worse than or close to UR, for instance in document degree estimation in Reuters, NG20 and Wiki datasets. We highlight those RSEs using bold font in Table 3. This is because γ for these datasets are rather small, ranging between 0.7 and 1.1. When γ is larger, RW demonstrate a larger advantage, such as in KDDCUP data.

5.3 Average degree of Reuters

In the following we focus on the detailed analysis using one dataset, the Reuters data. Estimators are normally evaluated in terms of bias, standard error (SE), and rooted mean squared error (RSME). In the case of average degrees they are defined as

$$\begin{aligned} Bias(\hat{d})&={\mathbb{E}}(\hat{d})-d,\\ SE(\hat{d})&=\left[{\mathbb{E}} (\hat{d}-{\mathbb{E}}(\hat {d}))^2 \right]^{1/2},\\ RMSE(\hat{d})&=\left[{\mathbb{E}} (\hat{d}-d)^2 \right]^{1/2},\\ \end{aligned}$$

Since Bias ² + SE ² = RMSE ², and bias is negligible compared to SE according to Sect. 4 and our first experiment below, we have SE≈ RMSE. Thus except the first experiment where Bias, SE and RMSE are reported, in the remaining experiments we report SE only.

Average degrees are estimated on both UR and RW samples using sample mean estimator ${\langle \widehat{d} \rangle}_SM$ defined in Eq. 3 and harmonic mean estimator ${\langle \widehat{d} \rangle}_H$ defined in Eq. 3, respectively. Since the degrees of terms have a much larger CV than that of documents, RW estimator is better than the UR for terms, but slightly worse for documents.

5.3.1 Average degree of terms

The two estimators are tested on the data for 10 different sample sizes ranging between 10³ and 10⁴. For each sample size we repeat the experiment for 200 times and the results are plotted in Fig. 3. Panel A compares UR and RW using box plots. It shows that RW has a smaller variance consistently for all sample sizes. Panel B plots the distribution of the estimations in the last box of panel A when sample size is 10⁴. It demonstrates that (1) both RW and UR estimations follow normal distribution with the same mean value (233); (2) RW has a smaller variance than UR.

Fig. 3

Average term degree estimation by UR and RW samplings. a box plots for various sample sizes ranging between 10³ and 10⁴. Data consist of 200 runs for each sample size. It shows RW has a smaller variance for all different sample sizes. b histograms focusing on the last box in a when n=10⁴ for UR and RW. It shows that the estimations by RW and UR follow normal distribution whose mean is the true value 233, and RW has a smaller variance. c 10 estimation processes along with the estimated 95 % error bound calculated from Eqs. 14 and 17 respectively. It shows that mostly the estimations are within the error bound, and RW has a smaller variance

Since the estimations follow normal distribution, the 95 % error bound can be calculated as roughly twice of the standard error described in Eqs. 14 and 17. Panel C plots the error bounds along with 10 large samples, each with size up to 2 × 10⁵. Although 10 sampling processes are hardly discernible from each other in the plot, what we want to show is that mostly they are within the error bounds as predicted by Eqs. 14 and 17. The plot validates the equations for estimated variances, and gives another perspective explaining why RW is better than UR. We will elaborate this further in Sect. 6 This plot also helps us determine how large the sample should be to achieve a satisfactory estimation.

The bias, standard error, and RSME of the two estimators are tabulated in Table 4. It shows that indeed $\widehat{\langle d \rangle}_H$ has a very small bias as expected in Sect. 4.1.2 for most sample sizes except for the smallest ones. When the sample size is very small (n ≈ 1,000), RW has a positive bias. A closer inspection of the experiment data reveals that the small terms dictate the outcome of $\widehat{\langle d \rangle}_H$, but they can be hardly visited within a small number of RW steps. Nonetheless, even for small samples where n = 1,000 the overall indicator RMSE of RW is 117, still smaller than that of UR (132) as highlighted in bold font in Table 4. We also experimented with sample size n = 500 where RMSE of UR is slightly better than RW.

Table 4 Estimations of average term degree $\langle d\rangle=233$ over 200 runs for various sample size n

Table 5 Estimated average document degree $\langle d \rangle=109.97$

Another perspective to interpret the results is looking at the sample sizes that reach similar SEs from RW and UR methods. For instance when the sample size is 6,000, the SE of RW is 36.7005. On the other hand, UR needs more than 10,000 samples to achieve the same SE as highlighted in bold font.

5.3.2 Average degree of documents

Table 5 lists the standard errors of the 200 runs on document degrees for sample sizes ranging between 500 and 5,000. First of all both estimators ($\widehat{\langle d \rangle}_{SM}$ and $\widehat{\langle d \rangle}_H$) perform better than term degree estimation because of the small variation of document degrees (CV = 0.7). Since the standard error of UR is already rather small, there is little chance for RW to beat the UR samples.

However, UR sampling is only slightly better than RW sampling for the same sample size. If we include the cost of obtaining the random samples using algorithm such as MHRW, the total cost shall be much higher since samples can be rejected many times. In simple RW we only need to double the sample size to achieve better result achieved by UR samples. For instance, the standard error of 3,000 RW samples is 4.1151 (in bold font), while 1,500 UR samples can achieve similar standard error.

5.4 Population size

In this experiment again RW samples are compared with UR samples. For RW samples, the population size N for both documents and terms are estimated using Eq. 19, where γ is estimated using Eq. 24. For UR samples the same estimator is used except that γ = 0.

Tables 6 and 7 show the standard errors for term population and document population, respectively. For term population size, the estimations may be infinite for small sample sizes 500, 1,000 and 1,500 due to zero conflict (C = 0). For document population size, the smallest sample size is 2,500, no longer 500 as in other experiments because small size may not induce collision in both sampling methods. Correspondingly the number of repetitions of the tests in this experiment is reduced to 20.

Table 6 Population size of terms

Table 7 Population size of documents

In both term and document population size estimations, RW works better than UR in terms of standard error, even for the document size estimation where CV is not large. This is because for the same sample size n RW has larger expected collision, therefore smaller relative variance. In addition, RW needs smaller sample size to produce non-infinite estimations. In UR sampling the sample size needs to be greater than $\sqrt{2N}$ ⁴ so that collisions can occur and the estimate is not infinite. For RW sampling, large documents have higher probability of being visited, thus smaller sample size can also induce collisions.

6 Discussions

This paper shows that the biased sampling can be better than uniform sampling. In the past, people try to obtain uniform samples whenever possible, and resort to biased sampling such as PPS sampling only when uniform sampling is impossible (Salganik and Heckathorn 2004) or costly. The results of this paper suggest that in the context of hidden data sources, RW sampling instead of uniform sampling should be used, even when UR samples are readily accessible.

We explain this using average term degree estimation as an example. The sample distributions of the degrees are depicted in Fig. 4. Panel A is the degree distribution for UR sample, which resembles the distribution of the population as expected. Panel B describes the distribution obtained from RW sampling. The “Y” shape plot shows that the small terms still follow power law roughly, while the large terms, the popular words, can be sampled many times. In other words, both small terms and large terms are sampled multiple times but for different reasons. Rare terms are sampled because there are large number of them, even though each term has a very small probability of being sampled. Large terms are sampled because they have higher probability of being visited, even though there are only a few of them. Unlike UR samples where some types of terms, especially the very popular words, are included by chance, in RW samples both rare words and popular words are well represented in the sample.

Fig. 4

The term degree distributions of the samples obtained from UR and RW samplings. n = 10,000

We elaborate this point further using a simplified fictitious example to gain an intuitive understanding of the method. Instead of the full spectrum of the degrees, we assume a polarized scenario that contains only two kinds of nodes–one million of small nodes with degree one and ten large nodes with degree one million. This mimics the scale-free graph that has many small nodes and a few very large nodes. Suppose that the sample size n is 10⁴ (1 % of the population). In both UR and RW sampling, the expected estimations are close to 11, the true value.

In UR sampling, the probability of a node being visited is p ≈ 1/10⁶ when one sample node is taken. When n = 10⁴ samples are taken, the number of times a node is sampled follows binomial distribution B(n,p) whose expectation is np = 10⁻². Thus the expected number of small nodes being sampled is 10⁻² × 10⁶ = 10⁴, the expected number of large nodes being visited is 10⁻² × 10 = 0.1. However, we can not have 0.1 number of node. Instead, most probably a large node is sampled zero or one time. Either case the estimation deviates from the real mean greatly as shown in Table 8. In Case 1 the large node is not sampled, resulting in the estimation 10. In Case 2 the large node is sampled once, resulting in the estimation 100 which is way larger than the expectation 11.

Table 8 Illustrative example where the graph contains 10⁶ small nodes whose degree is one, and 10 large nodes whose degree is 10⁶

On the other hand, in RW sampling the probability of a node being sampled is proportional to its degree. For a small node, the probability being sampled when one sample is taken is p _s  = 1/(11 × 10⁶). The probability of a large node being sampled is 10⁶ times larger, i.e., p _l  = 10⁶/(11 × 10⁶). Thus the expected number of times a small node being sampled is np _s  = 1/(11 × 10²), the expected total number of small nodes being sampled is 10⁶/(11 × 10²) = 909. The expected number of large nodes being sampled is 10 × np _l  = 9,091. Since the expected values are way larger than one, the estimates will not deviate a lot from the expected values.

7 Conclusions

This paper tackles the estimations of the average degree, the degree heterogeneity, and the population size in hidden web data sources. We show that the three proposed estimators are dependent on each other– population size is dependent on the heterogeneity, and in turn the heterogeneity relies on the average degree. Such decomposition of the estimation problem has not only the pedagogical significance, but more importantly, a large problem is divided into two smaller ones, and each sub-problem can be approached with different methods, not necessarily by RW.

The highlight of the paper is not the RW estimators. Rather, it is the comparison with the UR sampling. It shows that when the data follow Zipf’s law, the variance of the UR method diverges with the corpus size, while the variance of RW sampling grows logarithmically. In real graphs with moderate high CV such as term degrees in Reuters, the RW method is already much better than the UR samples, let alone the high cost of obtaining those uniform samples. In (Lu and Li 2012) we show that with higher CV and larger graphs, RW is orders of magnitude better than UR samples.

This paper shows that the behaviour of the RW method depends on the heterogeneity of the data. For term degrees whose variance is large (CV = 16), the RW method has a big lead over the UR method. For document degrees where the variance is small (CV = 0.7), the RW method is slightly worse than the UR samples if the cost of random sampling is excluded. In ecology studies the data reported usually have small heterogeneity whose γ² is around one. In our big data γ² is in the scale of hundreds or thousands. This big difference entails new methods that are drastically different from the traditional estimators such as the ones developed in (Chao et al. 1992).

For the population size estimation, RW is better than UR for both terms and documents in two perspectives. One is that in UR sampling the sample size needs to be greater than $\sqrt{2N}$ so that collisions can occur and the estimate is not infinite. For RW sampling, since large documents have higher probability of being visited in the RW, smaller sample size can also induce collisions, consequently produce non-infinite estimates. Secondly, the standard error of RW is smaller than that of the uniform sampling because the expected collisions are larger in RW.

Appendix

Both Theorems 1 and 2 assume that the degrees follow the Zipf’s–Mandelbrot law (Montemurro 2001) which states that if the term degrees d _i are sorted in descending order, then

$$d_i = \frac{A}{\alpha+i},$$

(26)

where α and A are constants. α ≪ N. All the degrees sum up to τ, i.e.,

$$\sum_{1}^{N} d_i \approx \int\limits_{1}^{N} \frac{A}{\alpha+x} dx \approx A \ln (\frac{\alpha + N}{\alpha+1}) =A\ln B=\tau,$$

(27)

where we use B = (α + N)/(α + 1) to make our derivations more concise. Therefore the normalizing constant $A=\tau/\ln B$. Besides, ∑ ^N₁ d ² _i can be approximated by the following since N is a very large number:

$$\sum_{1}^{N} d_i^2 \approx \int\limits_{1}^{N} \frac{A^2}{(\alpha+x)^2} dx \approx \frac{A^2}{\alpha+1}.$$

(28)

1.1 Proof of Theorem 1

Based on Eqs. 27 and 28, the variance of all the degrees is

$$\begin{aligned} \sigma^2 &=\langle d^2 \rangle-\langle d \rangle^2 = \langle d \rangle^2 \left[ N \frac{\sum_{1}^{N} d_i^2}{ (\sum_{1}^{N} d_i)^2} -1\right]\\ &\approx \langle d \rangle^2 \left[ \frac{N}{ (\alpha+1) \ln^2 B}-1 \right]. \end{aligned}$$

(29)

Using Eq. 14 the variance of $\widehat{\langle d \rangle}_{SM}$ is

$$var(\widehat{\langle d \rangle}_{SM})= \frac{\langle d \rangle^2}{n} \left[ \frac{N}{ (\alpha+1) \ln^2 B}-1 \right].$$

(30)

1.2 Proof of Theorem 2

When nodes are sampled with simple RW, the asymptotic probability of the node i being visited is p _i  = d _i / τ. When n nodes $(x_1, x_2, \ldots, x_n)$ are sampled, where each $x_i \in \{1, \ldots, N\}$, the Hansen–Hurwitz size estimator of the population size N is (Thompson 2012):

$$\widehat{N}_{H}=\frac{1}{n}\sum_{i=1}^{n} \frac{1}{p_{x_i}}=\frac{\tau}{n} \sum_{1}^{n} \frac{1}{d_{x_i}},$$

(31)

and the variance of $\widehat{N_H}$ is (Thompson 2012):

$$var(\widehat{N_H})=\frac{1}{n}\sum_{i=1}^{N}p_i\left(\frac{1}{p_i}-N\right)^2.$$

(32)

Replacing p _i with d _i /τ and expand d _i with A/(α + i), we have

$$var(\widehat{N_H})=\frac{1}{n} \left( \frac{\tau}{A} \sum_{1}^{N} i-N^2 \right) \approx \frac{N^2}{n} \left( \frac{\ln B}{2} -1\right).$$

(33)

The Taylor expansion of $\widehat{\langle d \rangle}_H$ around N is

$$\widehat{\langle d \rangle}_H= \frac{\tau}{\widehat{N_H}} = \tau \left( \frac{1}{N}-\frac{\widehat{N_H}-N}{N^2}+\cdots \right).$$

(34)

By the Delta method, the variance of $\widehat{\langle d \rangle}_H$ is

$$var(\widehat{\langle d \rangle}_H) =\tau^2 \frac{var(\widehat{N_H})}{N^4} = \frac{\langle d \rangle^2}{n}\left( \frac{\ln B}{2} -1 \right).$$

(35)

1.3 Population size estimation

Nodes are selected during RW. When selecting two nodes, the probability that the same node i is visited twice is p ² _i . Among all the nodes, the probability of having a collision is p = ∑ ^N _i=1 p ² _i . Since there are ${\left(\begin{array}{l} n \\ 2 \end{array}\right)}$ pairs in a sample of size n, the number of collisions follows binomial distribution B(n(n − 1)/2, p) whose mean is

$$E(C) =\left(\begin{array}{l} n \\ 2 \end{array}\right) p.$$

(36)

The collision probability p can be translated into the heterogeneity of the data measured by γ using the definition of γ in Eq. 12:

$$p=\sum_{i=1}^{N} p_i^2 =\frac{1}{\tau^2}\sum_{i=1}^{N} d_i^2 =\frac{1}{N}\frac{\langle d^2\rangle} {\langle d\rangle^2} =\frac{1}{N}(\gamma^2+1).$$

(37)

Combining Eqs. 37 and 36 we obtain the expected number of collisions is:

$$E(C) =\left(\begin{array}{l} n \\ 2 \end{array}\right)\frac{\gamma^2+1}{N}.$$

(38)

Hence the population size can be described by

$$N=(\gamma^2+1)\left(\begin{array}{l}n \\ 2 \end{array}\right) \frac{1}{E(C)}.$$

(39)

Since E(C) is unknown, it can be estimated by the observed collisions C. This gives us the estimator

$$\widehat{N}=(\gamma^2+1)\left(\begin{array}{l} n \\ 2 \end{array}\right) \frac{1}{C}.$$

(40)